寻思维起点揭问题本质
——对一道中考题变式分析及探索
☉江苏南京市雨花台区教师发展中心刘春书
寻思维起点揭问题本质
——对一道中考题变式分析及探索
☉江苏南京市雨花台区教师发展中心刘春书
解决问题的过程中经常会没有方向,思维迷茫,如何唤醒思维是我们一直所追寻的,只有静下来思考解题的思维起点在何处.另外问题得以解决不是终点,可能才是起点,只有让问题的条件从特殊到一般,尽管解法在减少,但本质在显现.笔者想通过一道中考题的变式分析及探索与大家一同来体验:“思维起点在何处?问题本质在何方?”
一、问题呈现
题目:(2014年武汉中考题改编)如图1,在四边形ABCD中,AD=4,CD= 3,∠ABC=∠ACB=∠ADC=45°,求BD的长度.
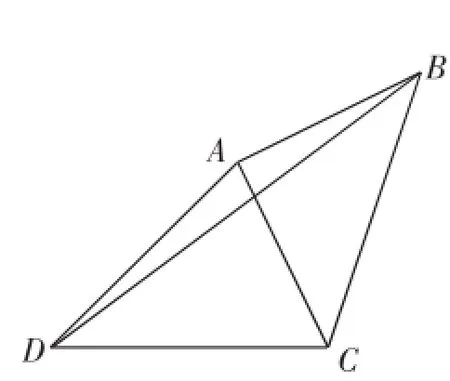
图1
二、思维的起点
1.思维的准备阶段.
(1)分析“条件是什么”.
认真审题,弄清题意,需将条件进行分解和重组,搞清楚条件是什么,能得到什么.比如本问题:
重组2:∠ABC=∠ACB=45°,可得AC=AB,∠BAC= 90°,又因为AC的长度是定的,所以△ABC为一个形状、大小确定的三角形(定三角形).
(2)研究“问题是什么”.
研究问题是什么,有必要用关联的视角去研究问题,关联的视角又是多维的.问题本身不是孤立的,与条件紧密联系,因此有必要从条件的视角研究问题是什么,分别研究问题与局部条件、问题与整体条件有何关联.比如本问题:与局部关联,可以认为BD是△ABD的一条边;与整体关联,可以认为BD是四边形ABCD的对角线.在此基础上思考解决问题需要什么.
(3)明确“定的是什么”.
每一个问题必有其定的元素,未明确时思维只能在外围打转,一旦基于定的元素思考,问题就至简至白.如何回归定的元素进行思考呢?就是基于条件思考不变的是什么,对于几何图形,一般研究形状、大小、位置,同时更要研究量与量、位置与位置之间的关系,尤其注意位置关系与数量关系的转化.比如,本题中“定”的有:如图1,(1)△ADC、△ACB、△ADB、△DCB、四边形ABCD的形状与大小;(2)AC与AB关于点A旋转对称;(3)∠ADC=∠ACB=45°的关系.
2.思维的联想阶段.
波利亚曾指出,好的思路大多来源于过去的经验和以前获得的知识.因此,不妨引导学生思考:“你是否曾遇到过与此相关的题目?”这个相关,并不一定是与一个曾经求解过的题目类似,而更可能是条件存在关联性,问题存在相似性,不仅是知识层面也可能是经验层面.因此,有必要源于“条件、问题、定的元素”去思考经验在哪里.本问题的经验有:
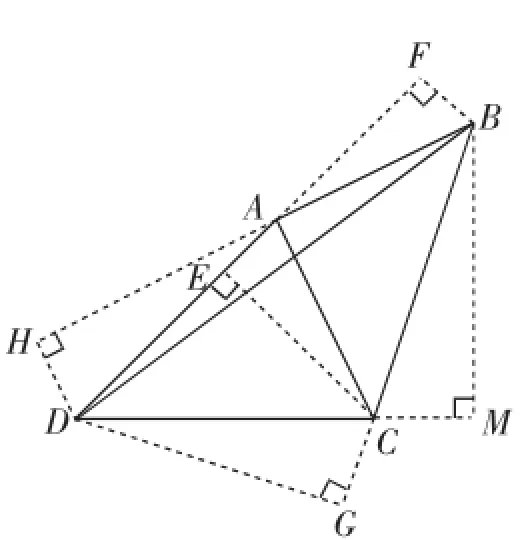
图2
经验1:知三求全,即已知三角形三个条件可以确定三角形的大小与形状,通过化斜为直便可求三角形中任何边、角及面积等所有元素.如图2,定△ADC可求AC;定△ACB可求BC.
经验2:求一条线段有两种常见的方法,一是利用相似,二是构造直角三角形利用勾股定理,两种方法都需要将BD边放入某一个三角形中,如图2,以BD为边的三角形有两个,分别为△ADB和△CDB,相似方法行不通,于是作高构造直角三角形,共有四种作法,是否有四种方法?需研究条件确定能否求直角三角形的两条直角边.
经验3:如图3(2),若C是线段AB的中点,A、B关于中点C中心对称,即可以构造中心对称图形,中点—三角形全等—平行四边形;如图3(1),若在线段AB上改变点C的位置,则A、B关于点C位似,位似比为AC∶BC,即可以构造相似;如图3(3),若将BC绕中点C旋转任意角度,则AC与BC关于点C旋转对称,即可以构造旋转全等.如图1,本题因为AB=AC,AB与AC就关于点B旋转对称.
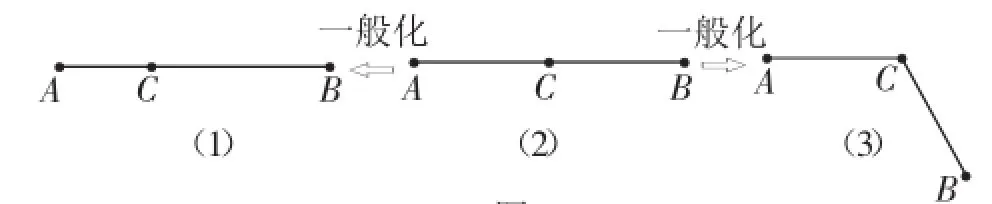
图3
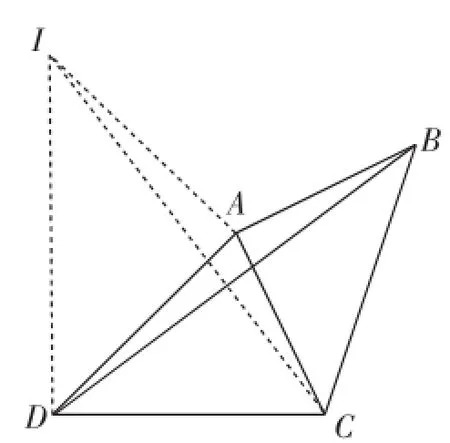
图4
三、思路及解法梳理
思路1:基于经验3用旋转对称解题.
方法1:如图4,过点A作AI⊥AD,垂足为A,使得AI= AD,连接DI、CI.
由∠ACB=∠ABC=45°,得AC=AB,∠CAB=90°.
由∠IAC=∠IAD+∠DAC,∠DAB=∠CAB+∠DAC,∠CAB=∠IAD= 90°,得∠IAC=∠DAB.
由AI=AD,∠IAC=∠DAB,AC=AB,得△AIC≌△ADB,则DB=CI.
由∠CDI=∠IDA+∠ADC=45°+45°=90°,得CI=
思路2:基于经验1和2解三角形.
方法2:如图5,作CE⊥AD,垂足为E;作BF⊥AD,垂足为F.
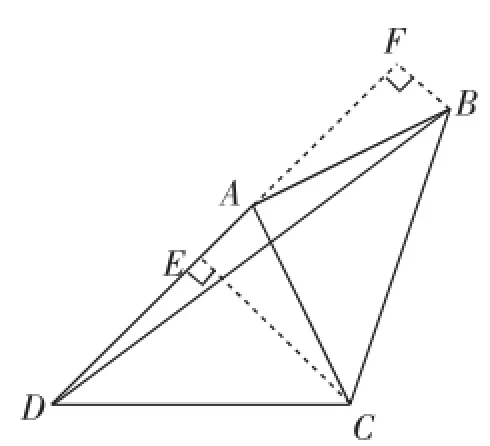
图5
由∠EAC+∠BAF=90°,∠EAC+∠ECA=90°,得∠BAF=∠EAC.
又AC=AB,∠F=∠CEA=90°,则△AEC≌△BFA,则BF=AE=1,AF=CE=3.
方法3:如图6,作CE⊥AD,垂足为E;作DH⊥AB,垂足为H.
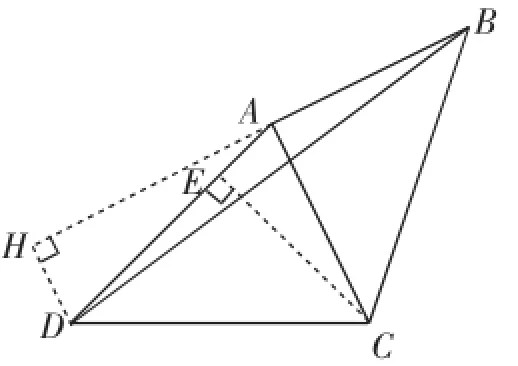
图6
由∠EAC+∠DAH=90°,∠HDA+∠DAH=90°,得∠HDA=∠EAC.
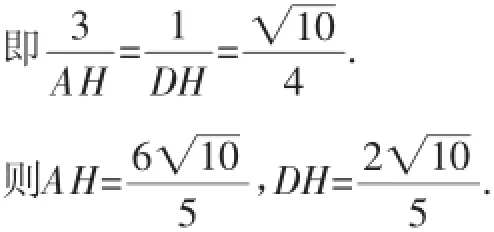
方法4:如图7,作CE⊥AD,垂足为E;作BM⊥DC,垂足为M.
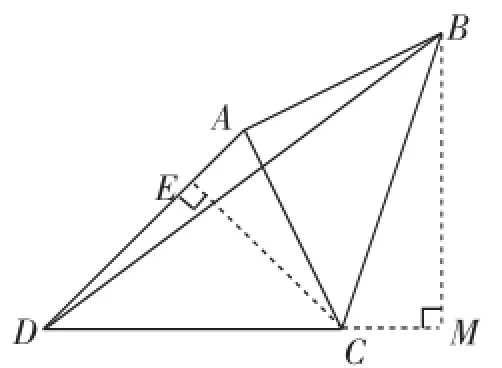
图7
由∠ACD+∠BCM+∠ACB=180°,∠ACD+∠CAE+∠ADC=180°,∠ADC=∠ACB,得∠BCM=∠CAE.又∠M=∠AEC,则△AEC∽△CMB.
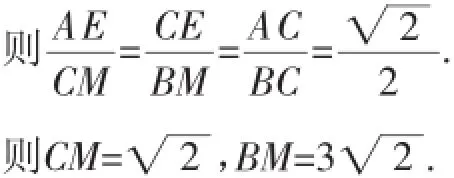
方法5:如图8,作CE⊥AD,垂足为E;作DG⊥BC,垂足为G.
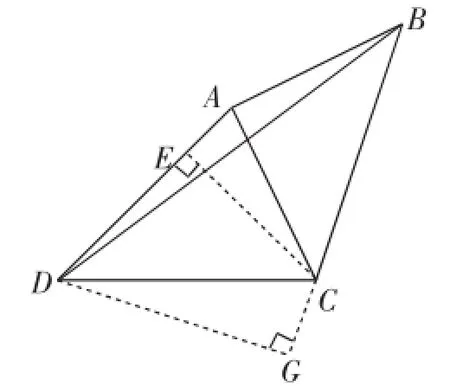
图8
由∠ACD+∠DCG+∠ACB=180°,∠ACD+∠EAC+∠ADC=180°,∠ADC=∠ACB,得∠DCG=∠EAC.又∠G=∠AEC,则△AEC∽△CGD.
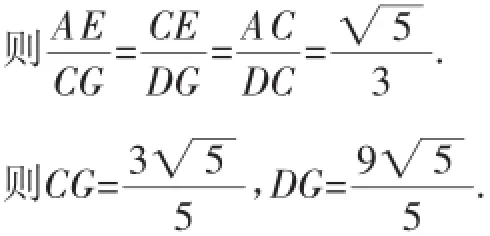
四、变式思考
两个定三角形拼成了一个定四边形,本题就是求定四边形对角线的长度,由旋转法可知本题是求一种特殊的四边形的对角线,最终化归为直角三角形由勾股定理可求.如果将本题进行一般化,也就是求任意四边形的对角线的长度,该怎么办?有必要研究问题的本质是什么,方得通性通法.
变式1:如图9,在四边形ABCD中,AD=3,,CD=4,∠ADC=∠ACB=45°,则BD的长度为_______.
解:作BE⊥CD,垂足为E;作CF⊥AD,垂足为F.
在Rt△FCD中,由CD=4,∠CDF=45°,得DF=CF=2.
由∠ACE是△ADC的外角,得∠ACE=∠ADC+∠DAC.又∠ACE=∠ACB+∠BCE,∠ACB=∠ADC=45°,则∠CAF=∠BCE.
又∠E=∠AFC=90°,则△AFC∽△CEB.
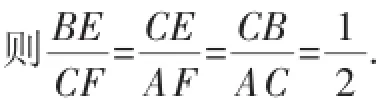
变式意图:原题具有很强的特殊性,无法体会问题的本质,弱化条件去掉AB=AC这一特殊的条件,就没有了旋转对称的条件,同时去掉∠BAC=90°,那么原来的方法2就不能再用.使得此类问题趋于一般化,求只满足一个特殊关系∠ACB=∠ADC的四边形的对角线长.
变式2:如图10,在四边形ABCD中,AD=3,CD= 7,BC=,∠ADC=45°,∠ACB= 90°,则BD的长度为________.
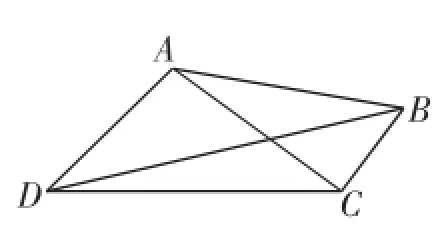
图10
解:作BE⊥CD,垂足为E;作AF⊥CD,垂足为F.
则CF=CD-DF=7-3=4.
在Rt△ACF中,则AF=3,CF=4,得CA=5.
由∠ACE是△AFC的外角,得∠ACE=∠AFC+∠FAC.又∠ACE=∠ACB+∠BCE,∠ACB=∠AFC=90°,则∠CAF=∠BCE.
又∠E=∠AFC=90°,则△AFC∽△CEB.
变式意图:变式1仍旧具有一定的特殊性,即∠ACB=∠ADC,基于特殊性得到了特殊的关系,从而利用相似刻画了∠BCE,求出CE与BE的长度.为达本质,有必要进一步弱化条件,使得∠ACB≠∠ADC,但是基于问题的难度可以将∠ACB特殊化,即∠ACB=90°,在此由基本经验2一线三直角,构图解决变式2,就是去特殊关系,留特殊值,为更一般化做准备.
变式3:如图11,在四边形ABCD中,AD=4■ 6,CD= 8+4,BC=2,∠ADC=45°,∠ACB=60°,则BD的长度为________.
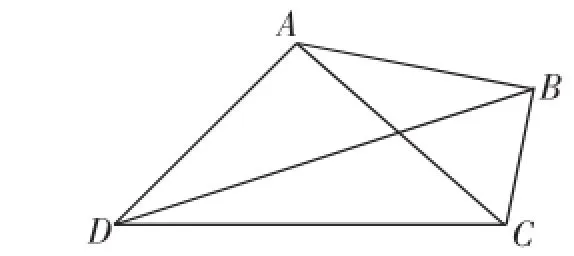
图11
解:作BE⊥CD,垂足为E;作AG⊥CD,垂足为G;在DG上取一点F,使得∠AFC=60°;作CH⊥AF,垂足为H.
在Rt△FHC中,由FC=12,∠AFG=60°,得FH=6,CH= 6.
则AH=AF-FH=2.
由∠ACE是△AFC的外角,得∠ACE=∠AFC+∠FAC.又∠ACE=∠ACB+∠BCE,∠ACB=∠AFC=60°,则∠CAF=∠BCE.
又∠E=∠AHC=90°,则△AHC∽△CEB.
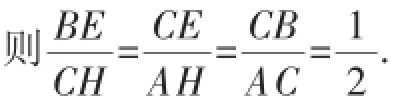
变式意图:变式1与2都具有一定的特殊性,基于特殊联想经验是可以解决问题的,要想触及问题本质,只有进行一般化,但是也要考虑初中学生现有的知识储备,因此从特殊角进行变式.如果问题依旧能得以解决,其实已达一般性,如果再进一步弱化,可以利用三角函数刻画∠ADC与∠ACB的大小,其问题解决的方法是一样的,变式3就是针对初中学生求任意定四边形对角线长度的通性、通法.
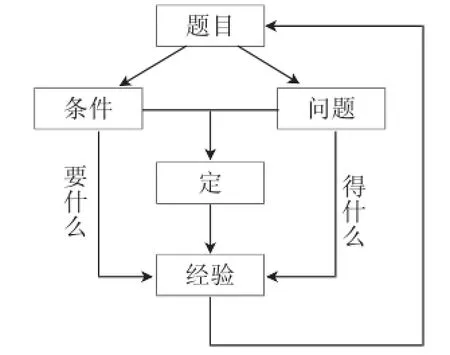
图12
2.如何基于“从特殊到一般”探本质、寻通法?
通过从特殊到一般的变式,在解法上从一般又回到特殊,因此,可以得出对于一个特殊问题会存在多种解法,但是问题趋于一般化时,问题的解法就会变少,最后留下来的方法就是问题的本质,比如本问题,就是解以BD为边的△BCD,基于现有的初中知识,只能化斜为直解直角三角形,其关键之处就是如何刻画∠BCD的邻补角,通过变式3可以发现基于定三角形创造出与其相等的角,进而用相似刻画角,最终化归为直角三角形.因此,解决四边形对角线的长需明确:(1)四边形的定是借助三角形的定,也就是两个定三角形组成一个定四边形;(2)求对角线的长,就是解关于对角线所构的三角形;(3)如图9,求BE与CE时需要借助定△ADC,构造定△ACF,在其过程中需要借助经验,即∠ACB=∠ADC时可得“K”形相似,进而得出∠CAF=∠BCE.通过本题变式发现基于“从特殊到一般”探本质、寻通法的思维导图如图13所示:
五、几点思考

图13
1.如何基于“波利亚解题原理”唤醒思维?
综观此题解法与变式的过程,从知识技能层面看,此题主要考查解三角形、相似形、旋转、三角形全等、勾股定理等知识.从能力层面看,此题主要考查学生的经验迁移能力、构图能力和推理能力.尤其,解决此题借助了探究三角形相似的过程中积累的方法和经验,特别需要用基本图形经验与思维经验相结合.如果学生从来没有体验过,那么解决这个问题还是很难的.因此问题的解决是经验先行,即经历对题目的分析,首先,思考条件是什么,从条件本身到条件重组思考定的数量或量与量之间存在的定的位置或数量关系;研究问题是什么,将问题放在局部或整体进行思考,问题是什么,基于问题解决需要定什么.最终,基于条件、问题、定的元素思考本题相关的经验是什么.基于“波利亚解题原理”发现迁移经验的思维导图如图12所示:
英国心理学家莱士的研究表明,解决问题要经历准备、孕育、明朗和验证这四个阶段.因此,问题的解决需要平时在教学的过程中多一些孕育的过程,就是积累经验,在问题明朗与验证的阶段需要强化条件,从一般到特殊寻找问题的解法与经验,然后弱化条件,从特殊到一般进行变式,从而剖析问题的本质,但是在问题一般化时其解法往往又是源于解决特殊所积累的经验.经验是问题的起点,本质是问题的终点,在此过程中需要特殊与一般相结合进行思考.
1.刘春书.弄清楚是什么,解法自然成[J].中学数学教学参考(中),2016(1/2).
2.刘春书.数学“哲学原理”在解题中给力[J].中学数学(下),2016(3).

