对锐角三角函数试题的背景分析与备考复习建议——以近几年全国各地中考试卷为例

☉宁夏银川市第十中学杨雄义

对锐角三角函数试题的背景分析与备考复习建议
——以近几年全国各地中考试卷为例

☉宁夏银川市第十中学杨雄义

本文以近几年全国各地中考数学试题为研究对象，对近几年全国各地中考数学试题中考查锐角三角函数的题目，从命题的背景、考查的特点、难易程度和命题方向等方面做了探讨，意在让广大师生明确中考锐角三角函数复习的目标、方向，帮助广大师生有效地进行中考复习.

一、问题的提出

纵观近几年全国各地中考试卷，锐角三角函数属必考内容，题目集中在对锐角三角函数概念及解直角三角形的考查，难度适中.本文通过洞悉全国各地中考数学试题中锐角三角函数试题考查的特点和命题方向，帮助广大师生有效地进行中考复习.

二、锐角三角函数概念题的考查特点及例题剖析

1.在直角三角形中考查锐角三角函数概念

锐角三角函数是学生学习勾股定理后，对直角三角形边、角关系的深入研究、升华和拓展，它为初中解直角三角形提供了工具，为高中学习任意角的三角函数奠定基础，起着承前启后的作用.在直角三角形中，考查锐角三角函数概念，用锐角三角函数概念求直角三角形的边或角，是各地中考基础题中常见题型.

例1（1）（2015·甘肃兰州）△ABC中，∠B=90°，BC= 2AB，则cos A=（）.

（2）（2016·湖南怀化）在Rt△ABC中，∠C=90°，sin A=，AC=6cm，则BC=（）.

（3）（2014·四川巴中）在Rt△ABC中，∠C=90°，sin A=，则tan B=（）.

2.在任意三角形中考查锐角三角函数概念.

在任意三角形中，运用相似三角形、圆等几何图形的特殊性质，通过寻找等角的方法考查锐角三角函数，是中考锐角三角函数概念命题的常见题型之一，解决这类题目的关键是构造直角三角形，找到相等的角，这类题目难度一般.

例2（1）（2013·湖北鄂州）如图1，Rt△ABC中，∠A=90°，AD⊥BC于点D，若BD∶CD=3∶2，则tan B=（）.

图1

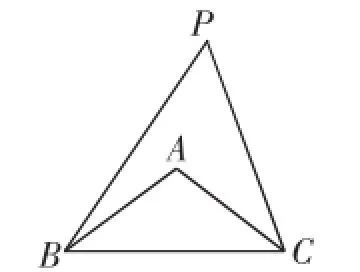
图2

（2）（2014·江苏苏州）如图2，在△ABC中，AB=AC= 5，BC=8.若∠BPC=∠BAC，则tan∠BPC=（）.

（3）（2014·上海）如图3，已知Rt△ABC中，∠ACB= 90°，CD是斜边AB上的中线，过点A作AE⊥CD，AE分别与CD、CB相交于点H、E，AH=2CH.

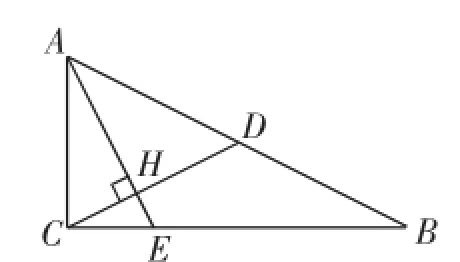
图3

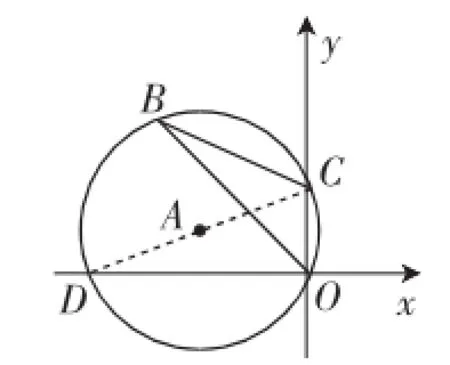
图4

（4）（2016·四川达州）如图4，半径为3的⊙A经过原点O和点C（0，2），B是y轴左侧⊙A优弧上一点，则tan∠OBC为（）.

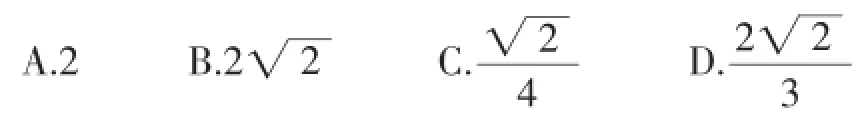
对于（1），运用了直角三角形角之间的关系、相似三角形的性质及参数法，只要找到∠B=∠DAC，问题便解决了；对于（2），运用等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合，过A作AD⊥BC，出现直角三角形，找到∠BPC=∠BAD就能得到结果；对于（3），运用直角三角形斜边上的中线等于斜边的一半，找到∠B=∠BCD=∠CAH，问题就能解决；对于（4），运用圆中同弧上的圆周角相等及直径所对的圆周角是直角，连接直径CD，利用∠OBC=∠CDO就能解决.

3.在网格中考查锐角三角函数概念.

由于正方形网格的特殊性，在网格中考查锐角三角函数，既可以考查特殊四边形的性质、勾股定理等知识，同时也能考查学生观察、分析、解决问题等综合能力，所以近几年这类题比较常见.2016年福州中考题将正方形网格变为菱形网格，是一种创新，解这类题的关键是利用特殊平行四边形的性质、勾股定理，通过添加辅助线构造直角三角形.这类题目解法灵活、有难度.

例3（1）（2016·贵州安顺）如图5，在网格中，小正方形的边长均为1，点A、B、C都在格点上，则∠ABC的正切值是（）.

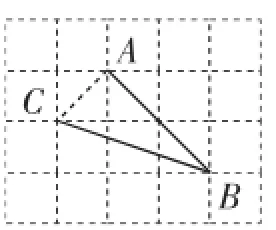
图5

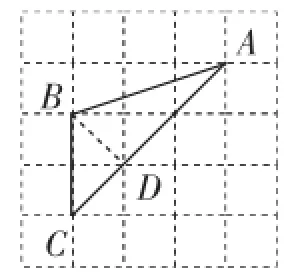
图6

（2）（2015·四川乐山）如图6，已知△ABC的三个顶点均在格点上，则cos A的值为（）.

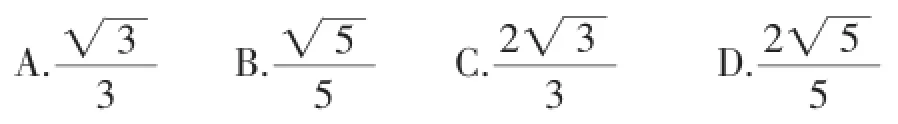
（3）（2016·四川自贡）如图7，在边长相同的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点P，则tan∠APD的值为________.

图7

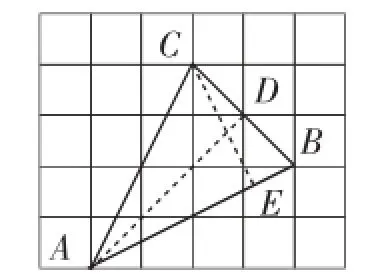
图8

（4）（2014·广西贺州）如图8，网格中的每个小正方形的边长都是1，△ABC每个顶点都在网格的交点处，则sin A=________.

（5）（2016·福建福州）如图9，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点.已知菱形的一个角（∠O为60°），A、B、C都在格点上，则tan∠ABC的值是________.

4.在小综合题中考查锐角三角函数概念.

以特殊几何图形为背景结合相似形、一元二次方程等知识考查锐角三角函数概念，我认为这是对学生数学综合素养的考查，既考查学生对图形的掌握情况，也考查学生综合运用知识分析、解决问题的能力，是近几年各地中考的常见题型，难度适中.

例4（1）（2013·四川攀枝花）如图10，在菱形ABCD中，DE⊥AB于点E，cos A=3 5，BE=4，则tan∠DBE的值是________.

图9

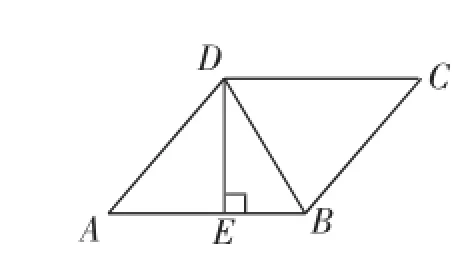
图10

图11

（2）（2016·四川绵阳）如图11，△ABC中，AB=AC=4，∠C=72°，D是AB的中点，点E在AC上，DE⊥AB，则cos A的值为（）.

（3）（2016·上海）如图12，矩形ABCD中，BC=2，将矩形ABCD绕点D顺时针旋转90°，点A、C分别落在点A′、C′处.如果点A′、C′、B在同一条直线上，那么tan∠ABA′的值为________.

图12

5.用锐角三角函数解决实际问题.

对于锐角三角函数的概念，初中的应用主要是解直角三角形，利用解直角三角形解决实际问题.在全国各地每年中考数学题中，这类题型是常见、常考题型.这类题的考查要求严格遵循新课标的要求，题目多数与仰角、俯角、坡度、坡角、方位角等结合，解题的关键是将实际问题转化为数学模型，通过构造直角三角形，利用勾股定理、三角函数解决，难度一般.

例5（1）（2015·辽宁大连）如图13，从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°，底部C的俯角为45°，观测点与楼的水平距离AD为31cm，则楼BC的高度约为_______m（结果取整数）.（参考数据：sin32°≈0.5，cos32°≈0.8，tan32°≈0.6）

图13

图14

（2）（2015·江苏苏州）如图14，在一笔直的海岸线l上有A、B两个观测站，AB=2km，从A处测得船C在北偏东45°的方向，从B处测得船C在北偏东22.5°的方向，则船C离海岸线l的距离（即CD的长）为（）.

（3）（2016·海南）如图15，在大楼AB的正前方有一斜坡CD，CD=4米，坡角∠DCE=30°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上.

①求斜坡CD的高度DE；

②求大楼AB的高度.（结果保留根号）

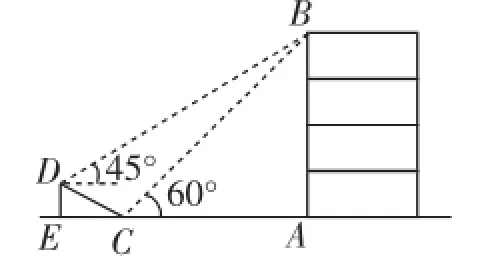
图15

图16

（4）（2016·山东菏泽）南沙群岛是我国固有领土，现在我南海渔民要在南沙某海岛附近进行捕鱼作业，如图16，当渔船航行至B处时，测得该岛位于正北方向20（1+）海里的C处，为了防止某国海巡警干扰，就请求我A处的渔监船前往C处护航，已知C位于A处的北偏东45°的方向上，A位于B处的北偏西30°的方向上，求A、C之间的距离.

三、备考建议

1.追本溯源，确立目标.

《义务教育数学课程标准（2011年版）》确定锐角三角函数的教学目标是：（1）利用相似的直角三角形，探索并认识锐角三角函数（sin A、cos A、tan A），知道30°、45°、60°角的三角函数值；（2）会用计算器由已知锐角求它的锐角三角函数值，由已知三角函数值求它的对应锐角；（3）能用锐角三角函数解直角三角形，能用相关知识解决一些简单的实际问题.课标是中考命题的依据，因此，我们在进行中考复习时，要认真研究课标，仔细推敲，确定复习目标和方向，不能遗漏任何一个知识点，注意在知识的交汇处设置问题，系统把握复习难度.

2.小题大做，注重本质.

纵观近几年各地中考考查锐角三角形的题目，内涵越来越丰富，知识交汇比较多，题目向综合性发展.但题目无论如何变化，考查锐角三角函数定义，解题的关键是寻找直角三角形、运用勾股定理.因此，我们要研究近几年各地中考题，对考查锐角三角函数的题目中有代表性的填空题、选择题进行归类、总结，小题大做、以小见大.复习时认真设置每一个例题，让学生能从题目中发掘、归纳、提炼出蕴含的解题方法、总结出解题规律.

3.因势利导，夯实基础.

分析近几年全国各地考查锐角三角函数的题目，都强调基础性，与教材中的习题联系紧密，多数题目都是对教材中习题的改编.因此，复习时要合理利用教材、发掘教材，对教材中的基础性习题做适当的变式，因势利导、夯实基础.

4.推陈出新，强化应用.

在小综合题中考查锐角三角函数是近几年各地中考命题的一种趋势，复习时我们要重视锐角三角函数与多种几何图形及知识的结合（如网格、特殊三角形、四边形、圆、相似形等），在知识的交汇点上下功夫，推陈出新.此外，各地考查三角函数应用的题目，都是解直角三角形的实际应用题，难度不大，学生容易上手，体现了对学生的人文关怀，复习时要强化对实际应用问题常规题目的学习.总之，锐角三角函数的复习，要突出锐角三角函数的工具性，注重学生数学能力的培养.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.