细谈怎样用活教材——以七年级“矩形、菱形、正方形”教学为例

☉江苏苏州工业园区第十中学沈单飞

细谈怎样用活教材
——以七年级“矩形、菱形、正方形”教学为例

☉江苏苏州工业园区第十中学沈单飞

教学实践表明，课堂教学必须考虑学生的学情，从学生已有的知识层面出发.因此，教师必须高屋建瓴，掌握教材深刻的内涵，在课堂教学中，把粗旷的教材通过教学过程转化为细微的知识；把主要集中于数学知识层面的教材，通过教学过程转化为思维训练和文化启迪；把普遍性、通用性的教材，通过教学过程转化为更有针对性和灵活性的范本.

一、教学简案

教学环节1：导入课堂，从中心对称性质和平行四边形切入.

质疑1：中心对称图形的概念是什么？平行四边形可以是中心对称图形吗？试试找出这些相关的平行四边形的对称中心.

创设存疑：具有中心对称的平行四边形，若旋转角度不是180°，你能够观察出旋转的角度吗？看看旋转过后的图形是否与原图形重合.

质疑2：（阅读课本，自学矩形、菱形、正方形的概念之后）思考在这三类图形中，四个角的度数、两条对角线之间的关系.

创设：板书矩形、菱形、正方形四个角的角度，以及两条对角线之间的关系，并整理几何语言进行课件呈现，安排学生填空：

例1如图1，在任意四边形ABCD中，边AB、BC、CD、DA的中点分别是E、F、G、H.

（1）若使四边形EFGH为菱形，需要添加条件__________，理由是_________.

（2）若使四边形EFGH为正方形，需要添加条件__________，理由是_________.

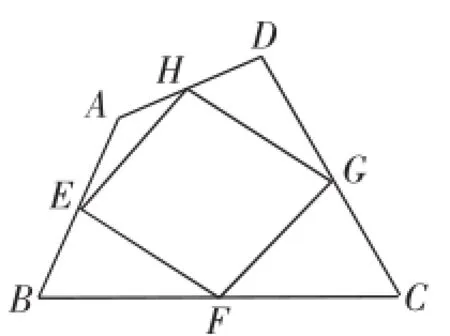
图1

创设存疑：若有AB=AD、CB=CD，你还能得出哪些结论？

创设意图：教材上对矩形、菱形、正方形四个角的角度，以及两条对角线之间的关系，简单提及过，学生对这类规律性的知识较为模糊，在案例中作为几何规律让学生深刻认识很有必要，让学生进一步去整理，有助于他们完善几何图形概念的认知.

教学环节2：课堂练习，强化概念认知.

例2判断以下命题的真假，请说明理由：

（1）两条对角线相等并互相平分的四边形是正方形.（）

（2）一条对角线平分一组对角的四边形是菱形.（）

（3）将四边形边的中点依次连接所得的四边形是平行四边形.（）

（4）等腰梯形的两条对角线相等.（）

创设意图：通过四个概念辨析的练习，让学生在对知识的回顾中加深对新学概念和性质定理的认知.然后可以跟进一组类似的课堂练习，这里略.

例3 E为矩形ABCD的边CD上一点，沿AE对折过来，如图2所示，若测得∠BAD′=30°，则∠AED的大小是________.

图2

图3

若测得∠BAD′=α°，则∠AED的大小是_________.

创设意图：作为计算题，本题主要训练学生对矩形的直角的分割，将部分折转化为轴对称图形，进而推出对应的角相等.为了训练这种计算或证明思路，夯实思维方法，进行变式练习.

变式练习1：图3为一张矩形纸片，若裁剪出一个最大的正方形，可以把矩形其中的一个角∠BAB′沿角平分线AE翻折上去，使B与AD边上的B′点重合.证明：四边形ABEB′就是一个最大的正方形.

教学环节3：典例讲评，细化再认.

例4如图4，四边形ABCD为菱形，AC、BD相交于点N，且AC∶BD=3∶4.若AB=4，求菱形ABCD的面积.

图4

创设意图：本题以教材例题为母题进行改编，首先引导学生证明△ABN是直角三角形，从而根据AB与两条直角边BN、AN之间的关系得出它们的长度，进而得出Rt△ABN的面积，再推出菱形ABCD的面积.在利用菱形的性质对其面积进行计算之后，引导学生反思推理路径，体会新定理带来的计算、推理的简捷.考虑到直角三角形与特殊四边形结合的推断计算题很多，可以为学生提供变式练习：

变式练习2：如图5，在菱形ABCD中，AB的垂直平分线MN交对角线AC于点N，垂足为M，连接DN.

（1）若∠BAD=70°，则∠CDN=____________.

（2）若∠BAD=β°，则∠CDN=____________.

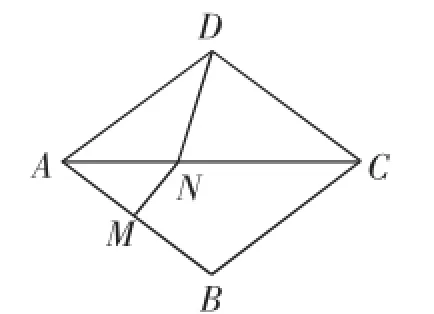
图5

图6

变式练习3：如图6，在矩形ABCD中，AB=6cm，BC= 3cm，点M沿AB边从点A开始向点B以1cm/s的速度移动；点N沿DA边从点D开始向点A以0.5cm/s的速度移动.如果M、N同时出发，用t s表示移动的时间（0＜t＜6），那么：

（1）当t为何值时，△NAM为等腰直角三角形？

（2）求四边形NAMC的面积.

（3）通过本题（2）的计算，请你总结出一条与计算结果有关的结论.

教学环节4：课堂小结，检测反馈.

小结质疑1：与平行四边形相比，本课中的矩形、菱形、正方形主要由四边形的什么性质探究而来？

小结质疑2：本课涉及的一些计算推断，你觉得用前面学习的什么知识作为“中介”比较合适？请在小组进行讨论与交流.

检测反馈题：如图7，在△ABC中，点O是AC边上（端点除外）的一个动点，过点O作直线MN∥BC.设MN交∠ACB的平分线于点E，交∠BCA的外角平分线于点F，连接AE、AF.

（1）当O点处于AC线段中的什么位置时，四边形AECF是矩形？

（2）证明你所给出的结论是成立的.

图7

二、课例创设感悟

1.课例是在深刻理解教材知识结构的基础上，创设课堂导入情境，与教材相比，是在矩形、菱形、正方形等几何图形概念导入之前，先诱导学生发现矩形、菱形、正方形是平行四边形及中心对称图形，并利用中心对称性质探究出定义、性质与判定；而教材却是用平行四边形的特殊变形来引出矩形、菱形、正方形的概念.因此可以说，教材有着承上启下的数学体系观隐含其中，那就是基于平行四边形的“特殊化”引出本节课的教学内容.也正是对这种“特殊化”的认识，在课堂教学中直接根据平行四边形的中心对称得出矩形、菱形、正方形等几何图形概念，能够开门见山，学生更容易将旧知与新知联系在一起.

2.淡化概念推理过程，创设题组强化概念.

考虑到矩形、菱形、正方形的四个角的角度，以及两条对角线之间的关系，主要是一种中心对称性体验，因此，在本课例中淡化了定义、性质与判定的推理过程，而从课堂变式练习、质疑串的形式来强化新概念.教材的设置与本课例的实践是相吻合的，教材没有过于强调概念的演绎过程，而是在简单给出概念之后直接应用.因此，本课例采用了大量的经典例题来强化几何图形的概念.

3.强化典例与变式拓展，及时检测与反馈.

教材上安排了一定量的例题，对应提升概念的认知来说题量还是有些偏小，针对教学实际情况，增加了一些中考试卷中的经典试题作为例题、变式练习，特别是对出现频率很高的直角三角形与矩形、菱形、正方形的综合考查问题，并在课堂小结阶段创设了检测反馈题，既强化了本课的概念，又从不同角度训练矩形、菱形、正方形的四个角的角度，以及两条对角线之间的关系的理解程度.

三、最后的感悟

总之，初中数学教材上很多知识、方法、思想藏而不露，需要在教学过程中通过转化达到锋芒毕露.教师虽然起着教材与学生之间的“桥梁”作用，但这座桥梁存在着一种特有的联系教材与学生的向心力.没有教师对教材的深入浅出的研究与分析，没有教师对知识的构建“过程”的点拨，学生只能浮在数学概念的表面，其“结果”只能是对数学感到茫然.因此，唯有教师“用教材教，用好教材、用活教材”，学生对数学的构建才能闯出一片蓝天.

1.田载今.平行四边形的定义、性质与判定［J］.中学生数理化（八年级数学），2014（3）.

2.张尊瑞.中考数学复习如何用活教材［J］.数学之友，2009（12）.

3.刘小伟，徐利根.矩形、菱形、正方形的判定和性质［J］.数学大世界（初中版），2013（5）.