一个猜想不等式的变元推广
2017-04-24 02:25:08张敬坤邮编457000
中学数学教学 2017年2期
张敬坤 (邮编:457000)
河南省濮阳职业技术学院
一个猜想不等式的变元推广
张敬坤 (邮编:457000)
河南省濮阳职业技术学院
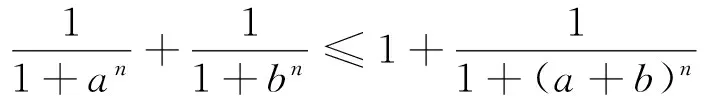
不等式;变元;推广
郭要红老师在文[1]末尾给出一个猜想,即



文[2]证明了该猜想是正确的,受文[2]启发.本文从变元上对这个猜想作了探究,得到一个更一般结果,即
定理 设ai>0,(i=1、2、3、…、m且m>1),n是正整数,若
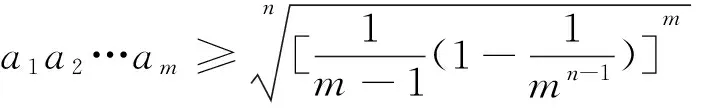
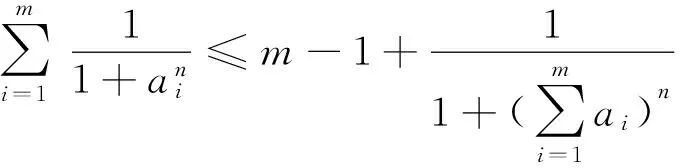

为证明定理,先给出两个引理:
引理1 (幂平均不等式)设xi>0,(i=1、2、3、…、m),p≥1,则

当且仅当x1=x2=…=xm时等号成立.


下面是定理的证明
证明 (1)当n=1时,


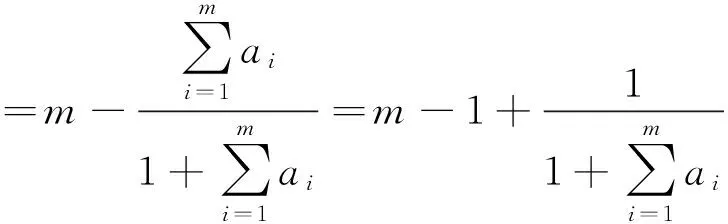
即定理成立.
(2)当n为不小于2的正整数时,因为


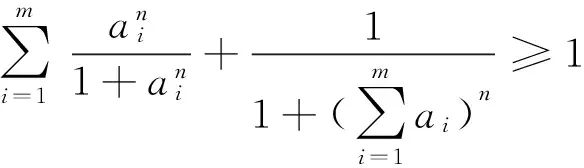
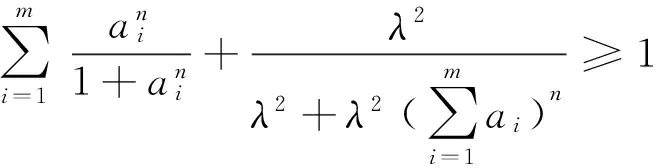


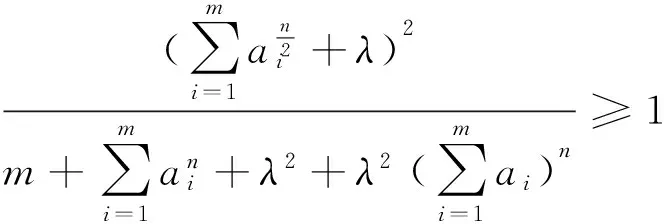

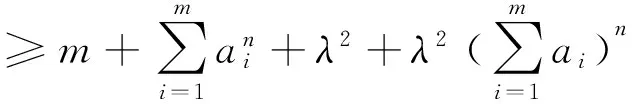


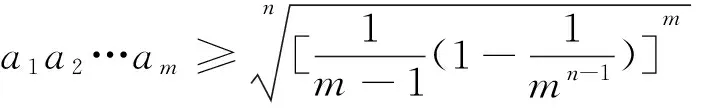

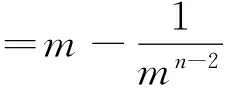

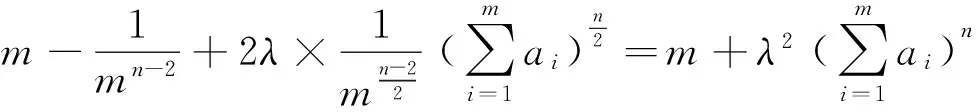
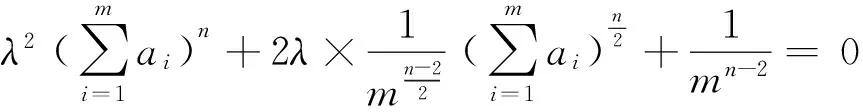
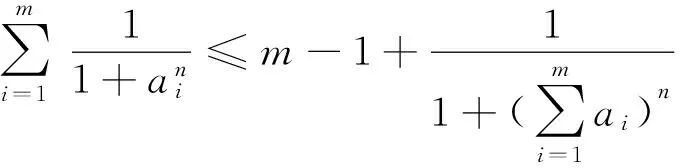
由(1)、(2)知定理成立.
在定理中令m=n=2,即是数学问题1869;令m=2,n=3,即得文[2]中的定理;令m=2,即是文[2]末尾的猜想.
1 郭要红.一个有理型不等式的类比[J].数学通讯,2011(9)(下半月)
2 李建潮.一个有理型不等式问题类比猜想的证明[J].河北理科教学研究,2013(6)
2016-12-23)
猜你喜欢
小学生学习指导(中年级)(2023年3期)2023-10-09 17:15:33
小学生学习指导(中年级)(2022年10期)2022-11-07 03:02:48
今日农业(2021年12期)2021-11-28 15:49:26
小学生学习指导·低年级(2021年6期)2021-09-10 16:36:45
语数外学习·初中版(2020年8期)2020-09-10 07:22:44
数学物理学报(2019年2期)2019-05-10 11:32:50
中国科技教育(2017年1期)2017-05-26 21:55:14
潍坊学院学报(2016年2期)2016-12-01 12:59:51
潍坊学院学报(2015年2期)2015-12-31 09:09:36
泰山学院学报(2015年6期)2015-06-07 11:09:41

