恒流源负载V2控制Buck变换器的稳定性分析

吴志敏,杨 艳,史国栋,包伯成,姚凯文

(常州大学信息科学与工程学院,江苏 常州 213164)

恒流源负载V2控制Buck变换器的稳定性分析

吴志敏,杨 艳,史国栋,包伯成,姚凯文

(常州大学信息科学与工程学院,江苏 常州 213164)

恒流源负载开关变换器在发光二极管照明领域具有广阔的应用前景，其研究具有理论意义和应用价值。为了研究电路参数对恒流源负载V2控制Buck变换器稳定性的影响，建立了该变换器的二阶离散迭代映射模型，得到了输出电容等效串联电阻、恒流源负载变化时的分岔图。分析结果表明，当输出电容等效串联电阻、恒流源负载变化时，恒流源负载V2控制Buck变换器具有复杂的动力学行为。利用特征值和最大李雅普诺夫指数对系统进行稳定性分析，验证了分岔分析的正确性。通过数值仿真得到了输出电容及其等效串联电阻之间的工作状态边界，揭示了输出电容时间常数稳定临界值与开关周期间的非线性关系。最后，基于PSIM电路仿真和电路试验，得到了输出电容等效串联电阻时的时域波形，验证了二阶离散迭代映射模型的有效性和理论分析的正确性。

电力电子； 二极管；恒流源负载; Buck变换器; 输出电容;稳定性分析

0 引言

发光二极管(light emitting diode,LED)照明是通过控制LED负载实现恒流照明[1]，在实际开关变换器中，LED负载可等效为恒流源负载，故恒流源负载开关变换器是今后电力电子的重要研究和应用方向。V2控制因其快速的动态响应而得到广泛关注[2]，因此，对恒流源负载V2控制Buck变换器进行深入研究具有重大的理论意义和应用价值。

开关变换器存在低频波动、次谐波振荡、倍周期分岔、边界碰撞分岔和不稳定混沌振荡等非线性动力学现象[3-6]。不稳定混沌振荡的出现会极大地影响开关变换器的控制性能，甚至导致开关变换器无法正常工作。因此，有必要运用动力学方法对开关变换器中存在的一系列非线性动力学现象进行研究，同时深入分析电路参数的变化对变换器稳定性的影响，以指导开关变换器的参数设计。

本文根据恒流源负载V2控制Buck变换器的状态方程，建立其二阶离散迭代映射模型。根据此模型研究了输出电容等效串联电阻(equivalent series resistance,ESR)R0和恒流源负载Io的变化对开关变换器的稳定性影响，分析了开关变换器存在的周期振荡、倍周期分岔、次谐波振荡、不稳定的混沌振荡等复杂物理现象[3-6]。电路参数范围和稳定性边界[7-9]对于变换器的电路设计和参数选择具有重要的指导意义。本文通过对输出电容ESR R0和输出电容C的仿真研究，得到了在R0-C平面上的工作状态区域分布图，并采用电力电子仿真软件(power simulation,PSIM)进行电路仿真和电路试验，以验证理论分析结果。

1 恒流源负载V2控制Buck变换器

1.1 工作原理

恒流源负载V2控制Buck变换器的电路原理图如图1所示。

图1 恒流源负载V2控制Buck变换器原理图

恒流源负载V2控制Buck变换器的功率级主电路由输入电压E、输出电容C及其ESR R0、开关管S、二极管D、恒流源负载Io和储能电感L组成[2]；恒控制电路由误差放大器、比较器、RS锁存器、时钟脉冲CP等组成。开关周期开始时，RS输出高电平，S导通，D关断，Uo增大。当Uo增大到Uk时，S关断至下一个开关周期开始[2,6]。由图1可知，当开关状态发生切换时，输出电压Uo满足：

Uo=Uk=K(Uref-Uo)

(1)

式中：Uref为参考电压；K为误差放大器的比例系数。

由式(1)可得，开关状态发生切换时的Uo为：

(2)

1.2 状态方程

根据开关管S和二极管D的开关状态，Buck变换器有3种工作模式：①S导通、D截止；②S关断、D导通；③S关断、D截止。在断续导电模式(discontinuous conduction mode,DCM)下，3种工作模式均存在；而在连续导电模式(continuous conduction mode,CCM)下，仅存在工作模式①和②。

设t=t0=nT为变换器在DCM模式下第n个开关周期内的初始时刻；t=t1为S从导通至关断、D从关断至导通的切换时刻；t=t2为D从导通至关断的切换时刻；t=t3=(n+1)T为该开关周期的终止时刻。τ1=t1-t0、τ2=t2-t1和τ3=t3-t2分别为3种不同开关状态内的持续时间。

则恒流源负载V2控制Buck变换器在第n个开关周期内的状态方程为：

(3)

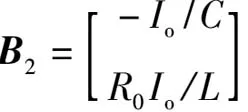
1.3 二阶离散映射模型

状态变量在t=t0=nT时刻的采样值为该开关周期的初值，可表示为xn=[Un,in]T；在t=(n+1)T时刻的采样值为该开关周期的终值，即下个开关周期的初值，可表示为xn+1=[Un+1,in+1]T。

首先，变换器进入工作模式①。根据式(3)的第一个方程，可得变换器经过时间间隔τ1后，在t=t1时刻的电容电压和电感电流分别为：U1(t1)=e-ατ1[(Un-E)cos(ωτ1)+k1sin(ωτ1)]+E

(4)

i1(t1)=e-ατ1[(in-Io)cos(ωτ1)+k2sin(ωτ1)]+Io

(5)

随后，变换器进入工作模式②。根据式(3)的第二个方程，以式(4)、式(5)的结果为初值，可得变换器经过时间间隔τ2后,在t=t2时刻的电容电压和电感电流分别为：

U2(t2)=e-αt2[U1(t1)cos(ωτ2)+k3sin(ωτ2)]

(6)

i2(t2)=e-αt2{[i1(t1)-Io]cos(ωτ2)+k4sin(ωτ2)}+Io

(7)

最后，变换器进入工作模式③。根据式(3)的第3个方程，以式(6)、式(7)的结果为初值，可得变换器经过时间间隔τ3后，在t=t3时刻的电容电压和电感电流分别为：

(8)

i3(t3)=0

(9)

由V2控制Buck变换器的原理可知，当Uo(t1)=Uk时，开关管由导通切换为关断，故工作模式①至

工作模式②的切换条件为：

U1(t1)+R0i1(t1)-R0I0=Uk

(10)

由式(10)可借助数值计算方法求出τ1。当变换器工作于CCM时，τ2=T-τ1、τ3=0；而当变换器工作于DCM时，令式(7)中的i2(t2)=0，可求出τ2，则τ3=T-τ2-τ1。得到τ1和τ2后，根据式(4)～式(9),可分别得到τ1≥T、τ1+τ2>T、τ1+τ2≤T这3种情况下的二阶离散迭代映射模型。

当τ1≥T时，在第n个开关周期内，变换器始终运行在工作模式①，则此时二阶离散迭代映射模型为：

(11)

当τ1+τ2>T时，变换器于CCM工作，此时二阶离散迭代映射模型为：

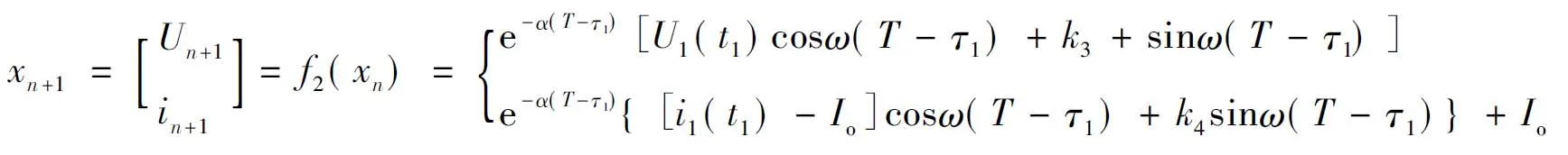
(12)

当τ2+τ2≤T时，变换器于DCM工作，此时二阶离散迭代映射模型为：

(13)

式(11)～式(13)构成了V2控制Buck变换器的二阶离散迭代映射模型。

定义变换器的输出电压边界Ub为在时钟周期开始时的输出电压值，在时钟周期结束时输出电压刚好到达控制电压Uk。结合式(4)和式(5)，可得边界值Ub为：

(14)

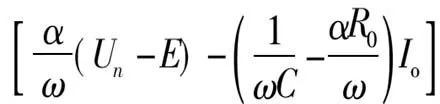
2 动力学行为分析

2.1 分岔分析

根据式(11)～式(13)的二阶离散迭代映射模型，选择表1所示电路参数，以输出电容ESR和恒流源负载为分岔参数，得到的数值仿真分岔图如图2所示。

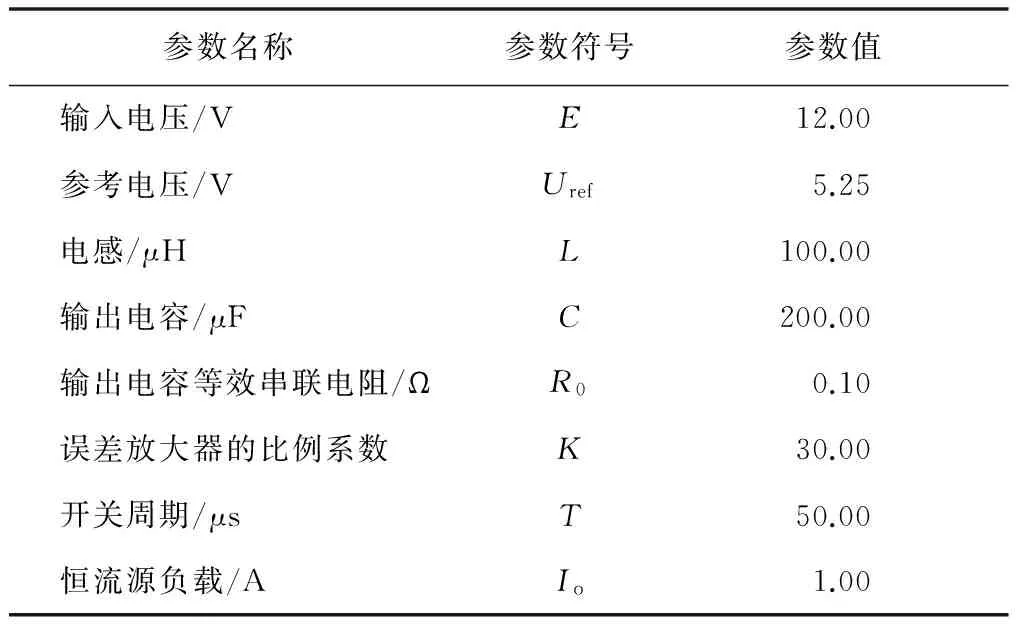
表1 电路参数

图2 数值仿真分岔图

图2(a)和图2(c)中，Io=1 A，R0=0.05～0.35 Ω。

当R0>0.284 Ω时，变换器工作在稳定的CCM周期振荡状态；随着R0的减小，在R0= 0.284 Ω处，变换器经倍周期分岔[10]进入到CCM次谐波振荡状态；在R0=0.27 Ω处，变换器发生工作模式转移，从CCM次谐波振荡状态进入DCM次谐波振荡状态；随着R0的继续减小，在R0=0.103 Ω和R0=0.085 Ω处，变换器的运行轨道与边界发生碰撞而引发边界碰撞分岔；在R0=0.072 Ω处运行轨道经边界碰撞分岔进入DCM混沌振荡状态。由分岔分析可知，通过增大R0，可使恒流源负载V2控制Buck变换器工作在稳定的CCM周期振荡状态。

图2(b)和图2(d)中:R0=0.1 Ω，Io=0.6～1.6 A。当Io<0.72 A时，变换器工作在稳定的DCM周期振荡状态；随着Io的增大，在Io=0.72 A处，变换器经倍周期分岔进入到DCM次谐波振荡状态；随着Io的继续增大，在Io=1.094 A和Io=1.388 A处，变换器分别发生了边界碰撞分岔和第二次倍周期分岔；在Io=1.43 A处，运行轨道经边界碰撞分岔进入DCM混沌振荡状态[10-12]。由分岔分析可知，通过减小恒流源负载Io，可使恒流源负载V2控制Buck变换器工作在稳定的DCM周期振荡状态。

2.2 稳定性分析

对离散迭代映射模型不动点处的雅克比矩阵及其特征根进行分析，可确定开关变换器稳态工作时的稳定性[2]。令xn+1=xn=XQ，恒流源负载V2控制Buck变换器的离散迭代模型在不动点XQ处的雅克比矩阵为：

(15)

式中：J11=∂Un+1/∂Un;J12=∂Un+1/∂in;J21=∂in+1/∂Un;J22=∂in+1/∂in。

以τ1≥T时为例，在第n个开关周期内，变换器始终运行在工作模式①，则矩阵系数Jij(i，j=1,2)分别为:

J11=e-αT[cos(ωT)+αsin(ωT)/ω]

(16)

J12=e-αTsin(ωT)/ωC

(17)

J21=-e-αTsin(ωT)/ωL

(18)

J22=e-αT[cos(ωT)-αsin(ωT)/ω]

(19)

根据所得雅克比矩阵，可得相应的特征方程为：

det [λI-Jn(XQ)]=0

(20)

由式(16)得到的2个特征值λ1和λ2的变化，可判定恒流源负载V2控制Buck变换器的稳定运行参数区间。

表2给出了Io=1 A，R0=0.28～0.29 Ω时的特征值。从表2可以看出，随着R0逐渐增大，离散迭代映射模型的一个实数特征值从-1进入单位圆，存在倍周期分岔现象。特征值走向分析结果与分岔分析一致，验证了分岔图的正确性。

表2 随R0变化的特征值

2.3 最大Lyapunov指数

Lyapunov指数是判断非线性系统存在混沌行为与否的重要手段[2,10-12]。恒流源负载V2控制Buck变换器的最大Lyapunov指数可表示为：

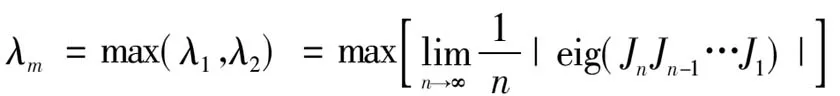
(21)

根据式(17)可知，与图2对应的最大Lyapunov指数谱如图3所示。

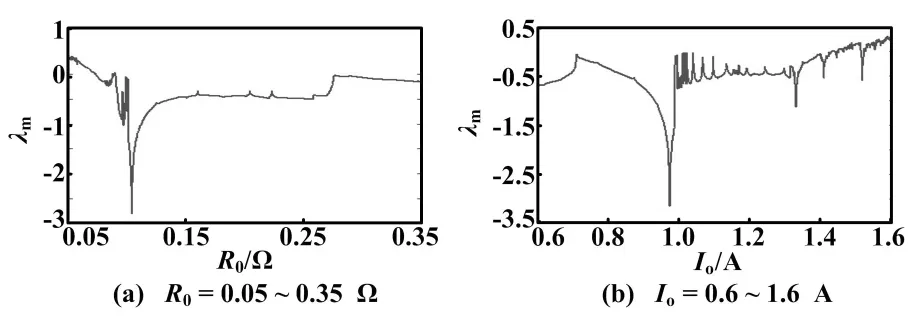
图3 最大Lyapunov指数谱

由图3(a)可以看出，当R0>0.072 Ω时，λm>0，变换器处于混沌振荡状态；当R0=0.085 Ω时，λm从负数上升到零，对应图2(a)中的第一次边界碰撞分岔点；当R0=0.103 Ω时，λm从负数上升到零，对应图2(a)中的第二次边界碰撞分岔点；当0.103 Ω

由图3(b)可看出，当Io<0.72 A时，变换器处于周期振荡状态；当Io= 0.72 A时，λm上升到零，对应图2(b)中的倍周期分岔点；当0.72 A1.43 A时，变换器处于混沌振荡状态，且在Io>1.43 A区间有小部分范围内λm<0，说明变换器存在周期窗。对比图2与图3，可以看出分岔分析结果与最大Lyapunov指数分析结果一致。

3 工作状态分析

由分岔分析可知，在R0减小的过程中，存在工作模式转移。通过Matlab与PSIM仿真，得到CCM下R0-C平面上的稳定与不稳定区域分布图如图4所示。

图4 稳定与不稳定区域分布图

R0-C平面上的工作状态边界值如表3所示。

表3 R0-C平面上工作状态边界值

由表3可知，恒流源负载V2控制Buck变换器中，R0的稳定CCM边界值随着输出电容C的变化而不断变化；R0×C的稳定边界值与开关周期T呈现非线性关系，与电阻负载V2控制Buck变换器有着显著区别。

4 电路仿真与试验验证

4.1 电路仿真

利用PSIM软件，搭建恒流源负载V2控制Buck变换器的仿真电路，并对其进行PSIM仿真。采用表1参数，其他电路参数保持不变，以R0为例，得到不同参数下的输出电压Uo的时域波形图如图5所示。

图5 PSIM仿真波形图

由图5(a)可知，当R0=0.3 Ω时，变换器工作在CCM周期振荡状态；由图5(b)可看出，当R0=0.05 Ω时，变换器工作在DCM混沌振荡状态。PSIM仿真结果与分岔分析结果一致。

4.2 试验验证

为进一步验证理论分析结果，以R0为例，选择与PSIM仿真相同的参数，建立相应的试验平台进行验证。误差放大器选用LM358N，比较器采用LM319，RS触发器采用芯片74ALS02，MOSFET开关管采用IRF3205N，选用IR2125芯片作为MOS管的驱动。为保证试验的准确性，试验操作时使用电子负载来替代恒流源负载和输出电容ESR。此外，时钟脉冲CP由双踪信号发生器提供。

保持其他电路参数不变，不同R0下输出电压纹波ΔUo时域波形图如图6所示。

从图6可看出，当R0=0.3 Ω时，变换器工作于CCM周期振荡状态；当R0=0.05 Ω时，变换器工作于DCM混沌振荡状态。随着R0的减小，变换器由CCM周期振荡状态转变为DCM混沌振荡状态。试验结果与PSIM仿真结果、分岔分析结果一致。

5 结束语

本文通过恒流源负载V2控制Buck变换器在3种工作模式下的状态方程，导出了它的二阶离散迭代映射模型，并基于该模型研究了输出电容ESR和恒流源负载对变换器的动力学特性影响。分岔分析结果表明：随着输出电容ESR的逐渐减小或恒流源负载的增大，变换器将逐渐从稳定的CCM周期振荡状态经倍周期、边界碰撞等分岔行为进入次谐波振荡状态，最终进入不稳定的混沌振荡状态。

通过特征值变化和最大李雅普诺夫指数研究了系统的稳定性。研究结果表明，输出电容ESR越大，变换器的工作状态越趋于稳定；输出电容ESR越小，变换器越容易进入到DCM混沌振荡状态，结论与分岔分析一致。此外，本文研究了在R0-C平面上的工作状态区域分布。PSIM仿真和电路试验很好地验证了理论分析的正确性。

[1] 周国华,许建平,包伯成,等.电流源负载电流控制Buck变换器的复杂次谐波振荡现象[J].物理学报,2011,60 (1):51-58.

[2] 何圣仲,周国华,许建平,等.输出电容时间常数对V2控制Buck变换器的动力学特性的影响[J].物理学报,2014,63 (13):25-36.

[3] 张希,许建平,包伯成，等.固定关断时间控制Buck变换器斜坡补偿技术及其机理研究[J].中国电机工程学报,2014,

34(36):6426-6434.

[4] 马正华,王国云,包伯成,等.脉冲序列控制反激式变换器边界碰撞分岔与电路参数估计[J].电工技术学报,2013,28(12):262-268.

[5] 包伯成,杨平,马正华,等.电路参数宽范围变化时电流控制开关变换器的动力学研究[J].物理学报,2012,61(22):220502.

[6] 史国栋,杨艳,张希,等.电感与负载对V2控制Buck 变换器的动力学影响[J].自动化仪表,2016,37(4):12-15.

[7] ZHOU G H,HE S Z,ZHANG X,et al.Critical output-capacitor ESR for the stability of V2 controlled buck converter in CCM and DCM [J].Electronics Letters,2014,50(12):884-886.

[8] BAO B C,ZHANG X,XU J P,et al.Critical Esr of output capacitor for stability of fixed off-time controlled buck converter[J].Electronics Letters,2013,49(4):287-288.

[9] BAO B C,YANG J,XU J P,et al.Effect of output capacitor ESR on dynamic performance of voltage-mode hysteretic controlled buck converter[J].Electronics Letters,2013,49(20):1293-1294.

[10]XIE F,YANG R,ZHANG B.Bifurcation and border collision analysis of voltage-mode-controlled flyback converter based on total ampere-turns[J].IEEE Transactions Circuits and Systems I:Regular Papers,2011,58(9):2269-2280.

[11]BAO B C,ZHOU G H,XU J P,et al.Unified classification of operation-state regions for switching converters with ramp compensation[J].IEEE Transactions Power Electronics,2011,26(7):1968-1975.

[12]ZHANG X,XU J P,BAO B C,et al.Asynchronous-switching map-based stability effects of circuit parameters in fixed off-time controlled buck converter[J].IEEE Transactions Power Electronics,2016,31(9):6686-6697.

Stability Analysis of V2Controlled Buck Converter with Constant Current Source Load

WU Zhimin,YANG Yan,SHI Guodong,BAO Bocheng,YAO Kaiwen

(School of Information Science and Engineering,Changzhou University,Changzhou 213164,China)

Switching converter with constant current source load has a wide application prospect in the lighting field of emitting diode,and therefore the study of V2controlled buck converter with constant current source load has theoretical significance and application value.In order to investigate the influence of circuit parameters on stability of V2controlled buck converter with constant current source load,a second order discrete iterative mapping model is established，based on which the bifurcation diagrams with the variations of the equivalent series resistance of output capacitor and constant current source load are obtained.The results show that the converter has complex dynamic behavior when the equivalent series resistance of output capacitor and constant current source load change.Stability of the system is analyzed by using the eigenvalues and maximum Lyapunov exponent,which validates the correctness of bifurcation analysis.The operation state boundaries between the output capacitor and its equivalent series resistance are obtained by numerical simulations,and the nonlinear relationship between the stable critical value of output capacitor time constant and the switching cycle is revealed.Based on PSIM circuit simulations and circuit experiments,the time domain waveforms under different equivalent series resistance of output capacitor are received.Thus,the effectiveness of the second order discrete iterative mapping model and the correctness of theoretical analysis are verified.

Power electronics; Diode; Constant current source load; Buck converter; Output capacitor; Stability analysis

常州市自然科学基金资助项目(CJ20159026)

吴志敏(1977—)，女，硕士，讲师，主要从事电能变换与控制技术的研究。E-mail:wuzhimin@cczu.edu.cn。 杨艳(通信作者)，女，在读硕士研究生，主要从事电能变换与控制技术的研究。E-mail:yangyan_Tiffany@163.com。

TH82;TP391

A

10.16086/j.cnki.issn1000-0380.201704017

修改稿收到日期：2017-01-16