基于BP神经网络的高精度陀螺恒流源补偿方法*
王健康,王雪涛,严 嵘,陈 斌,王春元
(北京控制工程研究所,北京 100190)
基于BP神经网络的高精度陀螺恒流源补偿方法*
王健康,王雪涛,严 嵘,陈 斌,王春元
(北京控制工程研究所,北京 100190)
为了提高陀螺恒流源精度,提出一种基于BP神经网络的陀螺恒流源补偿方法.采用BP神经网络训练恒流源控制指令与恒流源输出之间的非线性映射稳态模型,以实时估计恒流源输出偏差.设计恒流源控制指令补偿判据,当输出偏差超出设定裕度时,按比例对恒流源控制指令值进行实时补偿,使得恒流源输出更接近控制目标值,以实现更优的精度.通过实物在回路仿真验证了上述方案的有效性,并通过与传统对控制指令进行分段线性标定方法相比较,显示了上述方案的恒流控制优势.
陀螺;恒流源;BP神经网络;非线性模型;标定方法
0 引 言
恒流源是一类常用的基准源,其作用是向负载提供恒定电流,主要用于差动放大电路、脉冲产生电路和各种测试系统中,但这里所谓的“恒流”只是一种习惯叫法,并不是电流值绝对不变,而是指电流变化相当小、在一定的工作范围内能够保持足够的稳定性[1-2].随着半导体集成技术的发展,恒流源技术已在航空、航天等多个领域得到了广泛的关注,典型的应用有放大电路偏置电流的设置、负载的有源模拟、信号监测等[3-4].
一般在卫星控制系统测试设备中,为精确实现对陀螺信号的激励与采集,就需要设计专门的高精度恒流源模块来构建陀螺信号源[5-6],其中电流大小的调节通过发送的控制指令来实时控制,控制指令由恒流源模块上板载单片机接收并进行解析,而后通过DA模块产生一个稳定的模拟量,进而控制恒流源输出电流的大小.由此过程可以看出,恒流源的特性将直接关系到整个陀螺信号源模块的性能指标及正常工作.为提高卫星控制系统测试设备中陀螺信号源的恒流输出精度,传统的方法是对陀螺信号源的恒流源板进行标定,采用分段线性方法设计恒流源的控制指令与实际输出之间的一次函数关系,进而在实际使用中对控制指令进行修正.在这种标定方法中,将恒流源的控制指令输入与电流输出看作为近似线性关系,在精度要求不高的情况下很具有实用性,但这种方法只是粗略修正,并没有将恒流源板中各模块输入输出间的非线性关系表征出来,因而若线性分段太疏就会导致精度不足,分段太密又会增大标定工作量与程序的复杂度,所以上述分段线性修正方法在高精度的恒流源模块中仍具有一定的缺陷.
本文利用非线性建模补偿的思路,将陀螺恒流源模块视为一个黑箱,首先基于BP神经网络算法[7]训练恒流源控制指令与实际电流输出间的非线性映射模型,用以实时估计恒流源模块的电流输出,而后设计控制指令补偿判据,若恒流输出估计值未达到精度要求,则计算控制指令值与恒流输出估计值之间的偏差,按比例对控制指令值进行实时补偿,以此来确保恒流源的输出精度.经实物在回路仿真验证,本文所提的基于BP神经网络补偿方法能够在保证实时性的前提下,在-10 mA~+10 mA恒流输出范围内达到1 μA的恒流输出精度,在-70 mA~-10 mA、+10 mA~+70 mA恒流输出范围内达到4 μA的恒流输出精度,比起传统采用线性分段标定恒流源的方法,恒流控制精度提升了约2倍,因而在工程应用中更具优势.
1 陀螺恒流源模块
由于陀螺是一种精密的惯性测量设备,陀螺信号源的精度要求也必然很高,本文所涉及的陀螺信号源共有6组互相隔离的恒流源信号,分别用于供3+1S二浮陀螺和光纤陀螺使用,均要求恒流输出在-70 mA~+70 mA,其中-10 mA~+10 mA范围内要求恒流输出精度需优于2.5 μA,+10 mA~+70 mA和-10 mA~-70 mA范围内要求恒流输出精度需优于5 μA,这就对其核心部件——恒流源的提出了较高的精度要求与稳定度要求.
本文仅以3+1S二浮陀螺中的X陀螺恒流源为例进行介绍,图1为陀螺信号源的实现框图,其中FPGA负责与动力学控制器进行数据交互并且控制陀螺信号源的信号产生逻辑,DA采用的18位的高精度DA芯片,并且采用了高稳定性基准和采样电阻,由于星上部分采集电路并不兼容信号源输出的TTL电平信号,在调理模块中采用了运放进行接口匹配,运放选用的是低温漂、高线性度的仪表运放,此外在电源方面,采用独立的线性电源供电,并使恒流源电路地平面和其余设备地平面完全隔离,以保证恒流源电路的稳定性.最终,恒流源板电路输出电流的分辨率可达到1 μA,纹波稳定度优于±0.5 μA.

图1 陀螺信号源的实现框图Fig.1 Block diagram of the gyro signal source
2 基于BP神经网络的恒流源补偿方法
鉴于神经网络具有很好实时性与泛化能力,对任意非线性对象具有无限逼近的功能,且易于实现,本文即采用BP神经网络来训练恒流源指令输入与恒流源电流输出间的非线性映射稳态模型,该模型拓扑结构如图2所示,其中X表示模型输入,Y表示模型输出,p表示模型输入变量个数,q表示模型输出变量个数,N表示隐含层神经元个数.下面对模型的输入输出、样本采点、模型训练等具体设计分别进行介绍.
1)确定模型的输入、输出.由于上述模型的作用是为了计算恒流输出偏差,进而对控制指令进行补偿,因而可将模型设计为单输入单输出模型,即p=q=1,其输入变量为发给恒流源的控制指令值,输出变量为恒流源的电流输出值,两者之差即为恒流输出偏差的估计值,若估计值达到一定精度,利用该偏差估计值对控制指令按比例修正,即可得到理想的恒流输出结果.
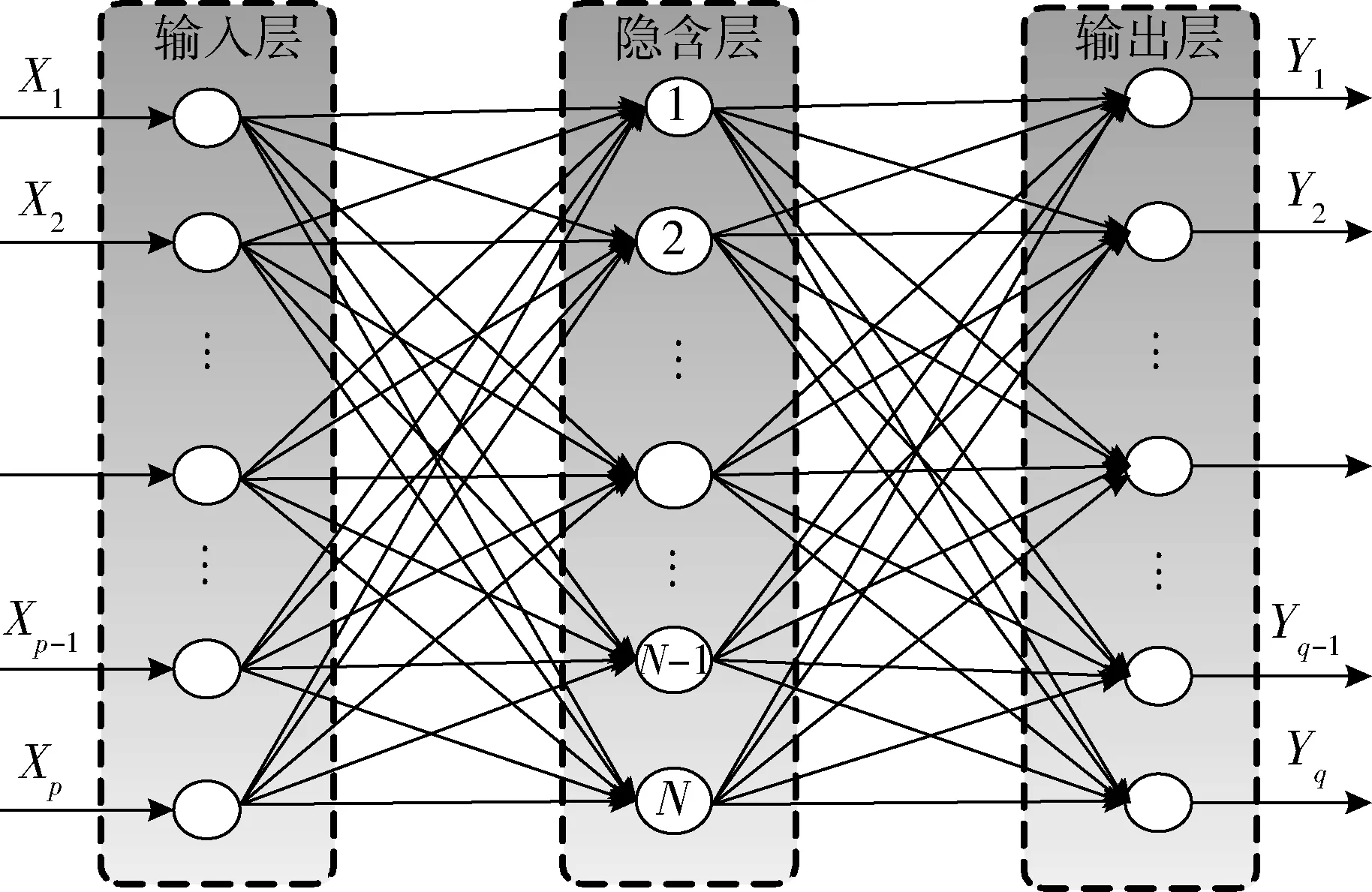
图2 BP神经网络拓扑结构图Fig.2 Sketch map of a BP neural network
2)设计样本采点.由于神经网络类似于一个非线性插值器,在内插时精度较高,而外插时精度较低,因而所选的训练数据应尽量包含各变量可能出现的最大最小值.根据陀螺信号源要求的恒流输出范围,选取恒流源输入指令范围为-70 mA~+70 mA,采点间隔0.5 mA,共计281个采点状态,以这些状态的恒流源输入指令为模型输入,恒流源输出电流为模型输出,并按5 ∶1的比例将其划分为模型的训练样本与测试样本.
3)模型归一化.为了提高模型精度,将模型输入、输出均作归一化处理[8],使模型输入参数、输出参数均处于0~1的数量级,而在模型实际使用过程中,对模型的输出进行反归一化处理即可.本文的归一化公式如下:
y=(y-ymin)/(ymax-ymin)
(1)
式中,y代表模型输入参数或输出参数,ymin代表输入参数或输出参数的最小值,ymax代表输入参数或输出参数的最大值.
4)确定模型的训练参数.本文通过调试法在神经元个数N=4~20的范围内进行训练精度比较,选取较优的BP神经网络训练参数,最终选择神经元个数N=15,最大训练步数Eepochs=1 500,训练目标最小误差Ggoal=1×10-15,这样设计的目的是为了使模型训练精度达不到该Ggoal的数量级,从而使模型得到最大步数的充分训练迭代计算,以尽可能提高模型精度,即在模型训练步数达到1 500后,结束模型训练.最终,该模型的训练结果如图3所示,其中图3(a)与图3(c)为模型归一化时的训练误差E1-train与测试误差E1-test,图3(b)与图3(d)为模型反归一化后的训练误差E2-train与测试误差E2-test,此处的误差均为相对误差,表达式为
(2)


图3 基于BP神经网络的恒流源模型训练结果Fig.3 Test results of the constant-current source model based on BP neural network

3 实物在回路仿真
本文在卫星控制推进测试设备中,利用上述基于BP神经网络建立的恒流源模型来改善恒流源模块,实现对陀螺信号的激励与采集,其设计结构如图4 所示,其中X表示陀螺恒流源的控制指令输入,ΔX为其补偿量,X′表示控制指令的修正值,Y表示恒流源模型输出,η表示控制指令的补偿系数,i表示模型的迭代计算次数.
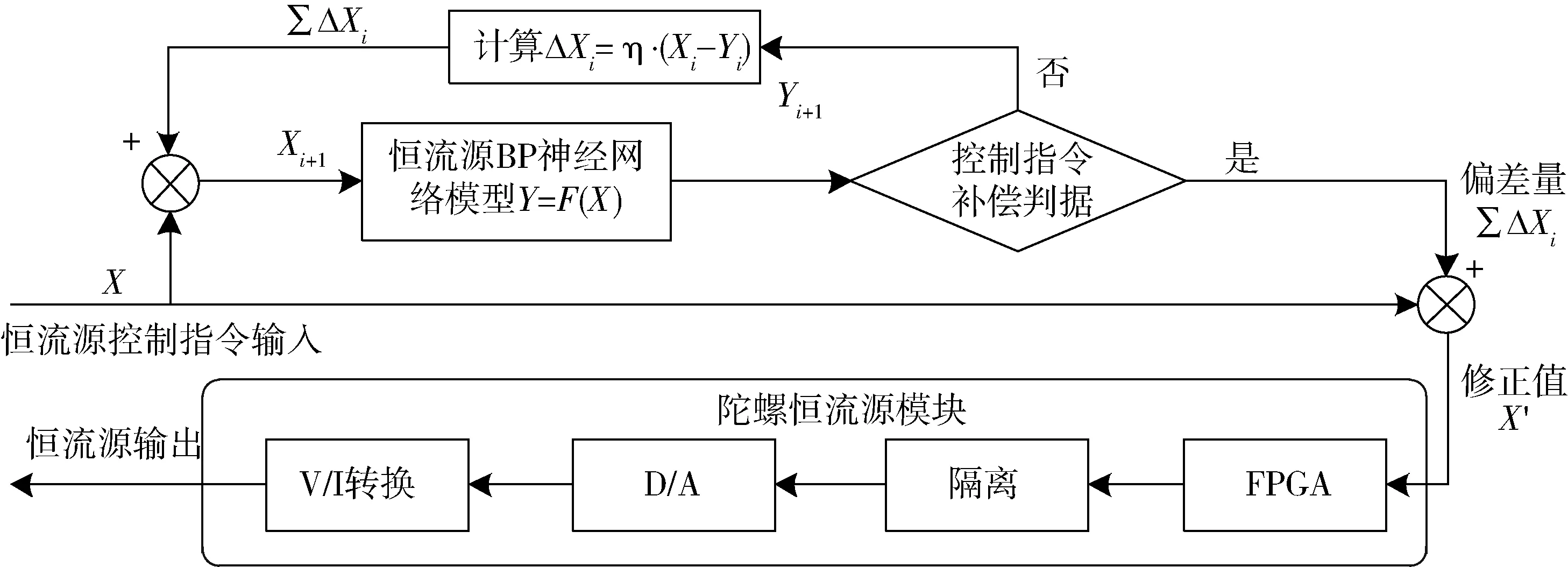
图4 基于BP神经网络补偿的陀螺恒流源设计结构图Fig.4 Gyro constant-current source implementation based on BP neural network compensation
从图4可以看出,由于恒流源BP神经网络的输出值Y仅是恒流源输出电流的估计值,无论模型达到如何高的精度,误差仍不可避免,因而本文在修正恒流源控制指令时设计了控制指令补偿判据,并非是一步修正到位,而是按比例逐步迭代修正,经验证如此设计更有利于提升模型的输出精度并减少模型迭代次数.本文设计的控制指令补偿判据如下:
1)首先预设定一个较小的判读裕度ε=0.1 mA,用来判断恒流输出是否满足精度要求,若达不到要求则在最大迭代次数内进行模型的迭代计算,不断修正模型输入;
2)预设模型最大迭代次数M=100,若模型迭代次数达到了最高值,则停止模型迭代计算;
3)当模型输出Y与控制指令输入X的偏差大于ε时,按Xi+1=Xi+ΔXi,对模型输入进行更新,并进行下一次的模型迭代计算,直至Yi-X≤ε或者模型迭代次数大于M,停止迭代计算,其中ΔXi=η·(Xi-Yi),i∈[0,M],补偿系数η=0.1;
基于上述思路,本文将该方案应用到陀螺信号源设计中,并与传统的对恒流源控制指令进行分段线性标定的方法相比较,其结果如图5所示.其中,采点间隔为1mA,图5a表示未对恒流源控制指令进行修正的恒流输出偏差图,图5b表示对恒流源控制指令进行修正后的恒流输出偏差图,包括传统的线性分段修正法与本文的BP神经网络补偿法的试验结果.
传统的分段线性标定方法中各段的线性拟合参数(斜率k与截距b)见表1,按电流大小平均分为6段进行设计,实际使用中根据恒流源控制指令输入所在的分段范围,对控制指令执行Y=kX+b进行修正.
从图5(a)可以看出,未采取恒流源控制指令修正时,恒流源的输出精度较差,最大偏差为220μA,随着电流的增大偏差越大,具有近似的线性关系.再看图5(b),在-10mA~+10mA恒流输出较小时,采用线性分段标定方法可使恒流输出偏差小于2μA,而采用BP神经网络补偿方法可达到1μA以内;而在-70mA~-10mA、+10mA~+70mA恒流输出较大时,采用线性分段标定方法仅能达到8μA的恒流输出精度,而采用BP神经网络补偿方法则可达到4μA的输出精度.由以可以看出,采用BP神经网络补偿方法能够很好的实现陀螺恒流源输出控制效果,与传统分段线性标定方法相比,恒流输出精度提升了约2倍.
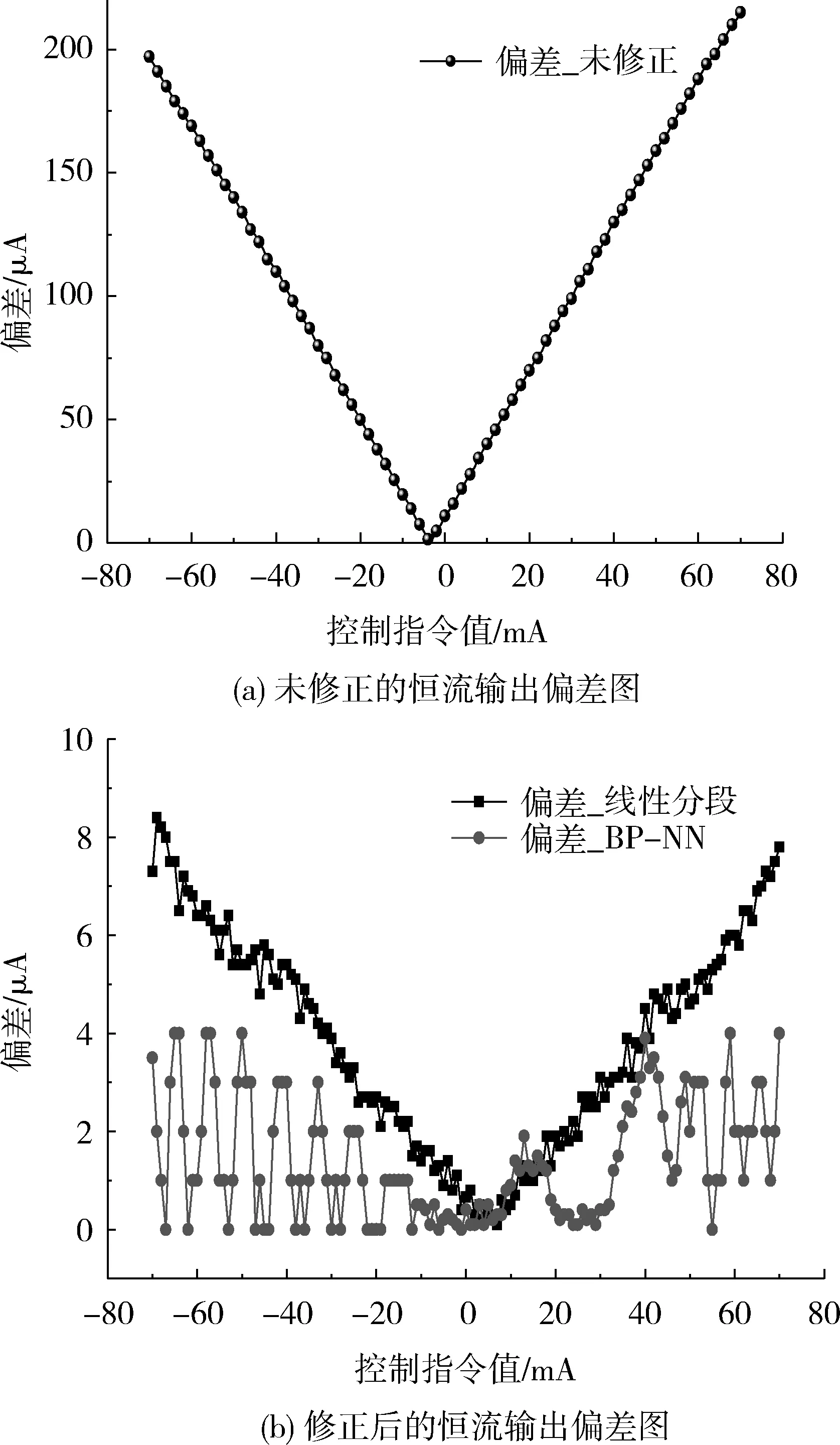
图5 基于BP神经网络补偿与基于线性分段标定的恒流源仿真比较Fig.5 Simulation comparison between BP neural network compensation method and segmented linear correction method

序号分段范围/mA斜率k截距b1-70~-401.0028890.0045532-40~-201.0030270.0102953-20~01.003050.0107940~201.0030070.010066520~401.0029960.010202640~701.0028710.015496
4 结 论
本文利用BP神经网络设计了陀螺信号源的恒流源模型,并以该模型为基础设计恒流源控制指令的实时修正策略,利用模型估计出恒流源输出偏差量,进而对恒流源控制指令按比例进行补偿.在实物在回路仿真试验中,通过与传统采用线性分段标定方法对比,体现了本文方法在恒流控制方面的有效性及优越性,并且由于设计方法的通用性,本文方法在其他领域的高精度恒流源设计中也具有很好的应用前景.
[1] 张洪川,滕召胜,林海军,等. 低功耗单电源压控精密恒流源设计[J]. 仪器仪表学报,2008,29(12):2678-2682. ZHANG H C, TENG Z S, LIN H J, et al. Design of precision voltage-controlled constant current source with low power dissipation single-supply[J]. Chinese Journal of Scientific Instrument, 2008, 29(12): 2678-2682.
[2] 秦玲,赖青贵,张良,等. 基于运算放大器的压控恒流源[J].强激光与粒子束,2010,22(3):553-556. QIN L, LAI Q G, ZHANG L, et al. Voltage controlled constant current source with operational amplifiers[J]. High Power Laser and Particle Beams, 2010,22(3):553-556.
[3] 王乐. 基于恒流源变送的应变测试系统研究[D]. 北京:北京科技大学,2009.
[4] 鲍玉军,钱显毅,何一鸣,等. 采用PID算法的高稳定恒流源设计[J]. 南京航空航天大学学报,2013,45(4):570-574. BAO Y J, QIAN X Y, HE Y M, et al. High-reliable constant-current source based on PID algorithm[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013,45(4):570-574.
[5] 王万峰,鲁浩,徐剑芸. 开环光纤陀螺信号处理[J]. 航空兵器,2008(6):20-22. WANG W F, LU H, XU J Y. Preliminary signal processing of the open-loop fiber optic gyroscope unit[J]. Aero Weaponry, 2008(6):20-22.
[6] 贾苹,李志宏.一种新型的光纤陀螺仪信号采集方法[J].中国惯性技术学报,2003,11(2):57-60. JIA P, LI Z H. A new method of data acquisition for FOG[J]. Journal of Chinese Inertial Technology, 2003,11(2):57-60.
[7] 吴简彤,王建华.神经网络技术及其应用[M].哈尔滨:哈尔滨工业大学出版社,1998.
[8] 黄喜元,王青,董朝阳. 基于归一化神经网络的航天器自适应姿态跟踪控制[J]. 宇航学报,2010,31(11):2542-2549. HUANG X Y, WANG Q, DONG C Y. Adaptive attitude tracking control for spacecraft based on input normalized neural network[J]. Journal of Astronautics, 2010,31(11):2542-2549.
The Design of Precise Gyro Constant-Current SourceBased on BP Neural Network Compensation
WANG Jiankang, WANG Xuetao, YAN Rong, CHEN Bin, WANG Chunyuan
(Beijing Institute of Control Engineering, Beijing 100190, China)
In order to improve the accuracy of gyro constant-current source, a compensation method of gyro constant-current source is proposed based on back propagation (BP) neural network. Firstly, with BP neural network, a nonlinear steady-state model that represents the relationship between the control input and the output of gyro constant-current source is trained. The model is used to estimate the output deviation of constant-current source. Secondly, a compensation criterion is confirmed, which is used to determine whether or not to modify the control command. Once the constant-current output deviation exceeds the margin, a certain proportion deviation is added up to the control command. Finally, the HIL(hardware-in-the-loop) simulation is carried out. The results show that the proposed method improves the output accuracy of the gyro constant-current greatly compared with the conventional piecewise linear correction method.
gyro; constant-current source; BP neural network; nonlinear model; correction method
*国家自然科学基金资助项目(61403030).
2014-10-21
TP3
A
1674-1579(2015)06-0047-05
10.3969/j.issn.1674-1579.2015.06.009
王健康(1986—),男,工程师,研究方向为卫星控制系统设计与测试;王雪涛(1972—),男,高级工程师,研究方向为卫星控制系统总体设计;严 嵘(1974—),男,高级工程师,研究方向为卫星控制系统总体设计;陈 斌(1986—),男,工程师,研究方向为卫星控制系统设计与测试;王春元(1982—),男,工程师,研究方向为卫星控制系统设计与测试.

