多刚体卫星转动惯量在轨辨识
许 莹,吕 旺,李云端,张大伟
(上海卫星工程研究所,上海 200240)
多刚体卫星转动惯量在轨辨识
许 莹,吕 旺,李云端,张大伟
(上海卫星工程研究所,上海 200240)
惯量辨识需要精确的动力学特性,针对动力学特性不可忽略太阳电池阵转动这一状况,提出一种惯量辨识方法,用于卫星本体惯量和太阳电池阵惯量的联合辨识.在建立多刚体姿态动力学基础上,针对辨识变量的耦合特性,推导带约束的优化辨识模型,再利用约束最小二乘算法求解.最后通过仿真计算验证了辨识方法的可行性.
多刚体姿态动力学;转动惯量辨识;约束最小二乘
0 引 言
卫星高精度姿态控制需要精确已知的惯量信息.地面人员在卫星发射前通过仿真计算和试验测量等方式获得卫星惯量信息.然而计算机辅助设计(CAD)软件(例如ProE)所建的模型与实际装配的卫星并不完全一致,使得惯量值存在计算误差;地面试验时由于重力以及测试设备本身的影响,所测惯量值不可避免地存在测量误差;在轨运行时活动部件转动、展开等动作以及推进剂消耗等因素都会引起惯量变化.因此,如何获得惯量的精确值是航天领域值得研究的技术之一.
目前国内外许多学者都开展了对于卫星转动惯量辨识的研究.Bergmann等[1-8]分别提出了基于递推最小二乘的在线辨识算法,以辨识惯量矩阵逆的各个分量;荆武兴等[9]提出了航天器转动惯量和质心位置的辨识方法,首次提出了参数可辨识性的分析方法;徐文福等[10]分别提出基于参数解耦的线性辨识算法和基于粒子群优化算法的非线性辨识算法.上述研究尽管都能够精确辨识惯量,但辨识模型大都是基于单刚体动力学,对于稳态运行的卫星而言,当太阳阵转速较大时,即使星体主轴惯量大于太阳阵主轴惯量,单刚体姿态动力学特性已不能准确描述星体的动力学特性.以中国已发射的风云三号气象卫星为例,太阳阵采用步进电机驱动控制,转速幅值最小为0.059(°)/s,而星体角速度约为0.006(°)/s,若仍根据单刚体动力学推导辨识方程,则不能精确辨识卫星惯量.因此,辨识模型中有必要考虑太阳阵转动的影响.
本文建立多刚体姿态动力学模型,针对卫星惯量时变特性,将太阳阵惯量从整星惯量中分离,推导线性定常系统的惯量联合辨识模型,再对模型可辨识分析,针对辨识模型非完整特性,提出应用约束最小二乘算法对惯量进行辨识的方法,并通过仿真计算验证算法的有效性.
1 卫星姿态动力学
将整星系统简化为包括本体、飞轮和太阳阵在内的多刚体模型,基于角动量定理建立多刚体姿态动力学方程.
1.1 坐标系定义
定义地心惯性坐标系Oi-XiYiZi,星体质心系Ob-XbYbZb,附件系Op-XpYpZp,太阳阵质心系Oa-XaYaZa,具体含义详见参考文献[12].太阳阵绕+Yc轴旋转,转角为+180°的卫星构型,如图1所示.
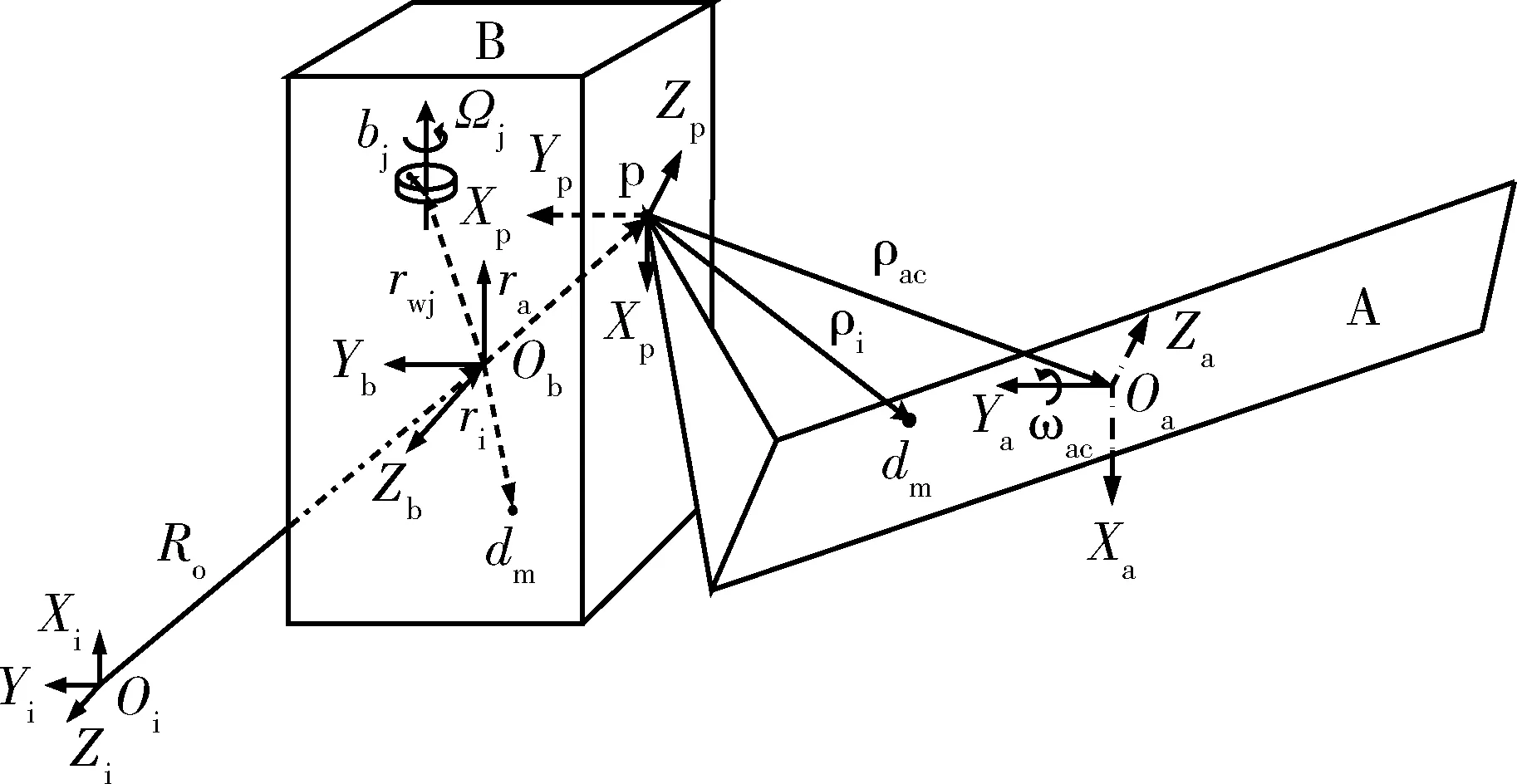
图1 多刚体模型卫星构型Fig.1 Multi-rigid body model of satellite
图1各矢量含义如表1所示.

表1 矢量定义
1.2 多刚体姿态动力学
多刚体姿态动力学模型[13-16]如下所示:
(1)
式中,Tde为环境干扰力矩项,Tdx为未知干扰力矩项.定义太阳电池阵相对本体转角为α,t时间转角为α=ωat,则太阳电池阵到本体系转换矩阵Cba为
(2)
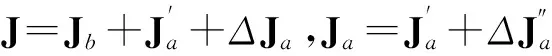
(3)
代入式(1),得
(4)
2 惯量辨识
惯量辨识方法是在建立辨识模型的基础上,根据辨识输入输出数据,利用辨识算法求解变量.
2.1 辨识模型
若辨识变量为本体惯量,则辨识问题就可以简化单刚体惯量辨识,在此不再赘述.若辨识变量为整星惯量矩阵的各个分量,则无法得到变量独立的线性辨识模型.因为方程含有太阳电池阵转动相关项,在太阳电池阵转动不可忽略情况下,整星惯量具有时变特性,因此无法辨识.为解决这一难题,本文针对本体惯量和太阳电池阵惯量的联合辨识问题进行研究.将太阳电池阵惯量从整星惯量中分离,基于动力学模型推导线性定常的辨识模型.假设辨识变量X由本体惯量和太阳电池阵惯量的12个分量构成,即
X=[JbxxJbyyJbzzJbxyJbxzJbyzJaxx
JayyJazzJaxyJaxzJayz]T
含义如下:
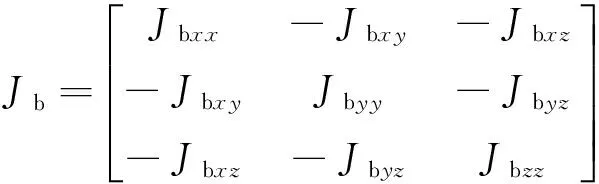
(5)
式(1)恒等变形为
(6)

X=[JaxxJayyJazzJaxyJaxzJayz]T≜
[j1j2j3j4j5j6]T
(7)
(8)
辨识输入输出等辨识已知信息如表2所示.

表2 辨识已知信息
2.2 可辨识性分析
上述联合辨识模型带入一次采样数据只能得到3个方程,无法直接求解12个变量的问题.考虑多次测量构成超定方程组,基于最小二乘原理求解.假设变量X维数为M×1,一次测量方程如下:
bi=aiX+υi
(9)
式中下标i记为第i次测量(i=1,2,3,…,N).bi维数为3×1,ai维数为3×M,υi为测量噪声,维数为3×1.利用N个采样点的数据构建超定方程组:
B=AX+V
(10)
式中各矢量表达式如下:
(11)
最小二乘原理简化表达如下:
minJ(X)=(B-AX)T(B-AX)
(12)
针对多刚体模型仿真,秩的结果如下:
rank(A)=11,rank([A,B])=12
(13)
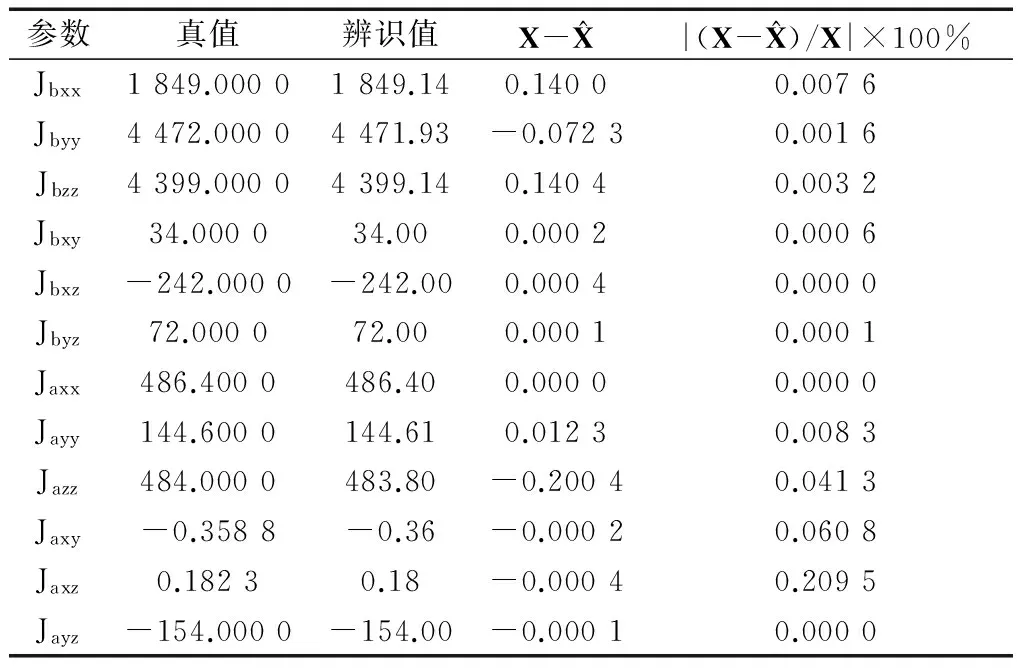
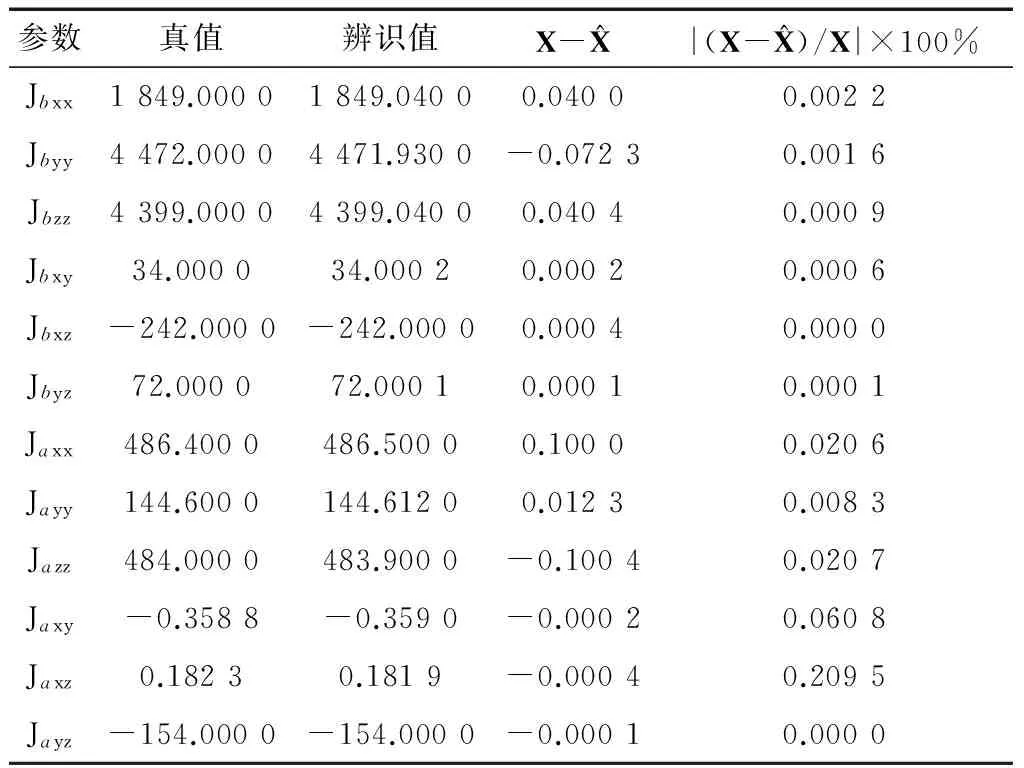
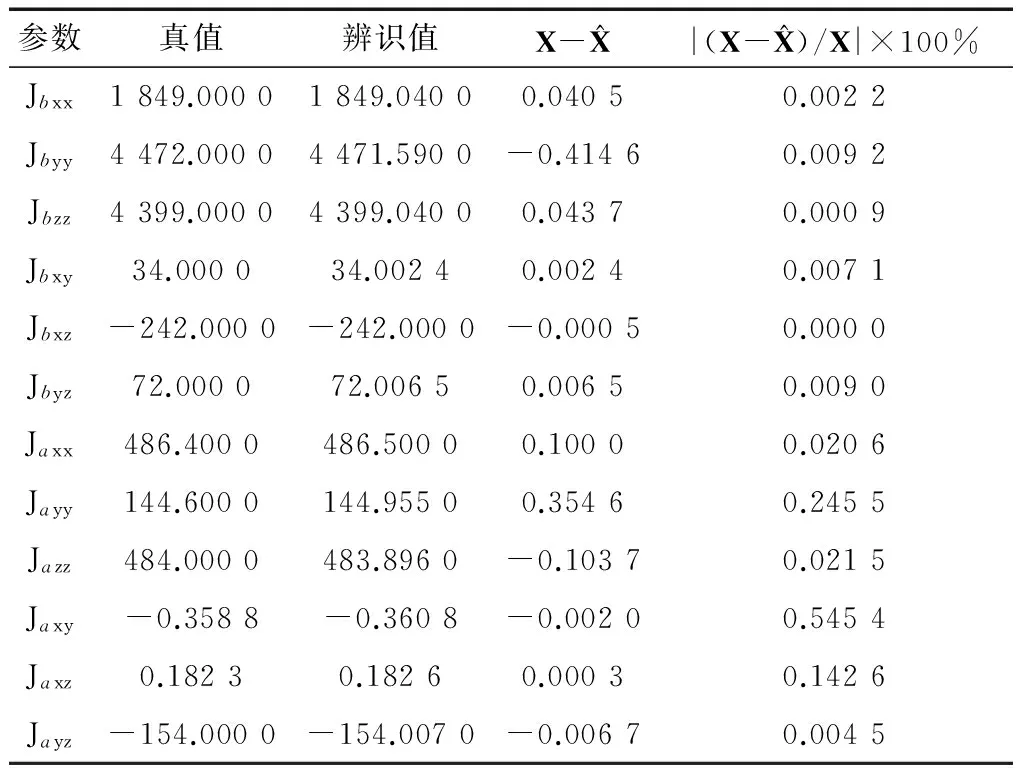
此时rank(A) A(:,1)-A(:,7)+A(:,3)-A(:,9)=0 A(:,1)-A(:,7)≠0,A(:,3)-A(:,9)≠0 A(:,1)-A(:,3)≠0,A(:,7)-A(:,9)≠0 (14) 系数矩阵第1、3、7、9列分别对应辨识变量Jbxx,Jbzz,Jaxx,Jazz,第一式特点表明这4个变量中存在耦合变量.若Jaxx已知,通过上式中的第二式和第三式提供的辨识信息可以辨识出Jbxx,Jbzz,Jazz.为解除上述变量的耦合关系,考虑增加辨识约束,提出一种带约束的优化辨识模型. 首先构造目标函数 f(X)=AX-B (15) 其次确定约束条件.若太阳电池阵X轴方向惯量Jaxx精确已知,则目标函数和等式约束分别如下: (16) Aeq=[0 0 0 0 0 0 1 0 0 0 0 0], Beq=Jaxx (17) 若Jaxx已知某一范围l≤Jaxx≤u,则约束为: Aieq=[0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0], (18) 2.3 辨识算法 将不满秩线性系统的参数辨识问题转化为带约束的优化问题,在自变量满足约束条件的情况下实现目标函数的最小化.考虑如下的约束优化问题: minf(x),x∈S (19) xk+1=Gk(xk,xk-1,…xk-p+1),k=p,p+1,… (20) 式中,Gk为迭代函数,x1,x2,…xp为初始点,由于有p个点,上式称为p步迭代算法,p=1则称为一步迭代算法,如下所示: xk+1=Gk(xk) (21) 在构造迭代格式时,首先需要构造评价函数M(x)来比较迭代点xk和xk+1的优劣,在每一步迭代中满足以下条件: M(xk+1)≤M(xk) (22) 因此这种迭代算法为下降算法,通常M(x)=f(x).实际应用中的迭代格式如下所示: xk+1=xk+αkdk (23) 式中dk为搜索方向,αk为步长. 本文采用上述解决带约束的最小二乘问题,目标函数和约束分别如下: (24) (25) 式中Aieq,Bieq皆为不等式约束系数,Aeq,Beq皆为等式约束系数,lb,ub分别为变量上界和下界. 考虑四种辨识工况,前两种假设太阳电池阵惯量精确已知,根据是否考虑测量噪声,得到两组辨识结果;后两种假设太阳电池阵惯量已知某一范围,根据是否考虑测量噪声,得到另外两组辨识结果. 假设太阳电池阵惯量Jaxx为486.4kg·m2,不考虑陀螺测量噪声,辨识结果与分析见表3. 表3 等式约束时不考虑测量噪声辨识分析 由表3数据可知,在Jaxx精确已知条件下,本体惯量辨识结果中绝对误差最大为0.2 kg·m2. 假设太阳电池阵惯量Jaxx为486.4 kg·m2,考虑速率陀螺测量随机噪声0.2(°)/h,辨识结果与分析见表4. 表4 等式约束时考虑测量噪声辨识分析 表4分析结果表明在考虑测量噪声情况下辨识误差也非常小,但辨识精度有所下降. 假设太阳电池阵惯量Jaxx已知范围为486.3≤Jaxx≤486.5,不考虑测量噪声的情况下,辨识结果与分析如表5所示. 表5 不等式约束时不考虑测量噪声辨识分析 由上表数据可知,在Jaxx已知某一范围条件下,本体惯量辨识结果中绝对误差最大为0.1 kg·m2.与已知某一精确值条件下的辨识结果相比,Jaxx已知某一小范围得到的辨识结果更为精确. 假设太阳电池阵惯量Jaxx已知范围为486.3≤Jaxx≤486.5,即辨识时太阳阵主轴惯量Jaxx偏差范围为±0.1 kg·m2,考虑速率陀螺测量随机噪声0.2(°)/h,辨识结果与分析如表6所示. 表6 不等式约束时考虑测量噪声辨识分析 上表分析结果表明在考虑测量噪声情况下辨识误差也非常小.本体惯量辨识结果中绝对误差最大为0.21 kg·m2.若辨识约束改为Jxx,Jzz,Jazz其中任意一个已知精确值或者已知某一范围,同样能够精确辨识.由于篇幅所限,在此不再赘述. 以考虑噪声的辨识工况为例,仿真120 s的辨识数据分别如下所示: 图2 本体惯性角速度变化Fig.2 Angular velocity n of body 图3 本体惯性角加速度变化Fig.3 Angular acceleration of body 图4 飞轮力矩变化Fig.4 Torque of wheels 图5 飞轮其角动量变化Fig.5 Momentum of wheels 本文研究带太阳电池阵的卫星惯量辨识方法,在建立带约束条件的优化辨识模型的基础上,基于约束最小二乘算法精确求解本体惯量和太阳电池阵惯量在内的12个变量值.所有辨识工况下得到的辨识结果中,绝对误差最大约为0.2 kg·m2,和真值相差3个数量级以上,辨识精度较高,说明辨识方法可行.尽管如此,后续研究仍有许多工作要做,例如对于多刚体模型假设的合理性有待进一步研究. [1] BERGMANN E V, WALKER B K, LEVY D R. Mass property estimation for control asymmetrical satellite[J]. Journal of Guidance, Control and Dynamics, 1987, 10(2): 483-492. [2] EDWARD W, CHRIS L, ROBERT W M. On-line gyro-based mass property identification for thruster controlled spacecraft using recursive least squares[C]//Proceedings of the 45thIEEE International Midwest Symposium on Circuits and systems. New York:IEEE, 2002: 1-4. [3] EDWARD W, SUTTER D W, MAH R W. Motion based on mass and thruster property identification for thruster controlled spacecraft[C]//Proceedings of the AIAA Infotech@Aerospace Conference. Washington D.C.: AIAA, 2005: 1-40. [4] TANYGIN S, WILLIAMS T. Mass property estimation using coasting maneuvers[J]. Journal of Guidance, Control and Dynamics. 1997, 20(4): 625-632. [5] WILSON E. Multiple concurrent recursive least squares identification with application to on-line spacecraft mass-property identification[P]. Redwood City, US 7110915B2. 2006. [6] 王书廷,曹喜滨.卫星质量特性的在线辨识算法研究[C]//第25届中国控制会议论文集.北京:中国自动化学会,2006: 519-524. WANG S T, CAO X B. On-line mass-property identification algorithm research for satellite[C]//Proceedings of the 25thChinese Control Conference. Beijing: CAA, 2006: 519-524. [7] 黄河, 周军, 刘莹莹. 航天器转动惯量在线辨识[J]. 系统仿真学报, 2010, 22(5): 1117-1120. HUANG H, ZHOU J, LIU Y Y. On-line Identification of Spacecraft Moment of Inertia[J]. Journal of System Simulation, 2010, 22(5): 1117-1120. [8] 荆武兴,韦文书,高长胜.基于陀螺测量信息的航天器突变参数识别方法[J].系统工程与电子技术,2013,35(9):1928-1932. XING W X, WEI W S, GAO CS. Identification of the mutation parameters for the spacecraft based on gyros[J]. Systems Engineering and Electronics 2013, 35(9): 1928-1932. [9] 徐文福,何勇,王学谦等. 航天器质量特性参数的在轨辨识方法[J].宇航学报,2010,31(8):1907-1914. XU W F, HE Y, WANG X Q, et al. On Orbit identification of mass characteristic parameters for spacecraft[J]. Journal of Astronautics, 2010, 31(8): 1907-1914. [10] 章仁为.卫星轨道姿态动力学与控制[M]. 北京航空航天大学出版社. 1998 [11] GILL P E, MURRAY W, WRIGHT M H. Practical optimization[M]. London: Academic Press, 1981. Identification of Rotary Inertia for Multi-Body Satellite XU Ying, LV Wang, LI Yunduan, ZHANG Dawei (Shanghai Institute of Satellite Engineering, Shanghai 200240, China) Accurate dynamics characteristics are important for rotary inertia identification. Considering the effect of solar cell array rotation in dynamics, a method of inertia identification is proposed, which is applied to identify the body inertia and solar cell array inertia simultaneously. Thinking of the coupling between the variables, the optimized identification model with constraint is deduced based on the modeled multi-body attitude dynamics. The precise solution is achieved via the algorithm of constraint least squares. Finally, the feasibility of the identification method is verified by simulation and calculation. multi-body attitude dynamics; rotary inertia identification; constraint least squares 2015-07-19 V44 A 1674-1579(2015)06-0031-06 10.3969/j.issn.1674-1579.2015.06.007 许 莹(1990—),女,硕士研究生,研究方向为航天器姿态动力学与控制;吕 旺(1983—),男,高级工程师,研究方向为卫星总体设计;李云端(1976—),男研究员,研究方向为卫星总体设计;张大伟(1980—),男,高级工程师,研究方向为卫星轨道、姿态动力学与控制、卫星总体设计.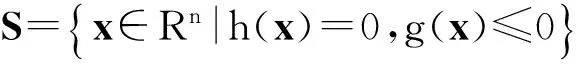

3 仿真分析
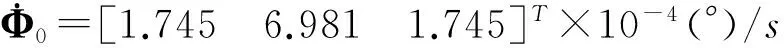



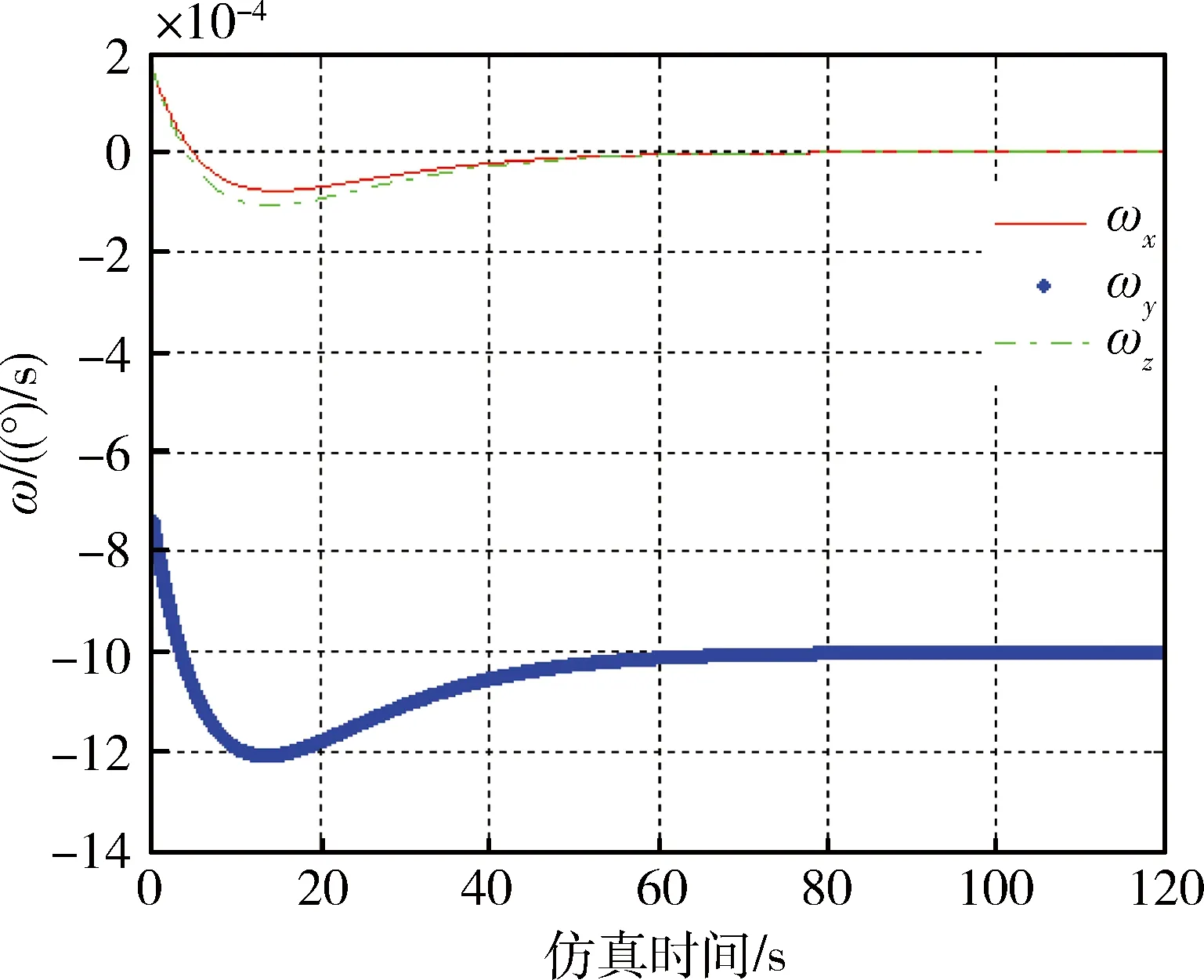
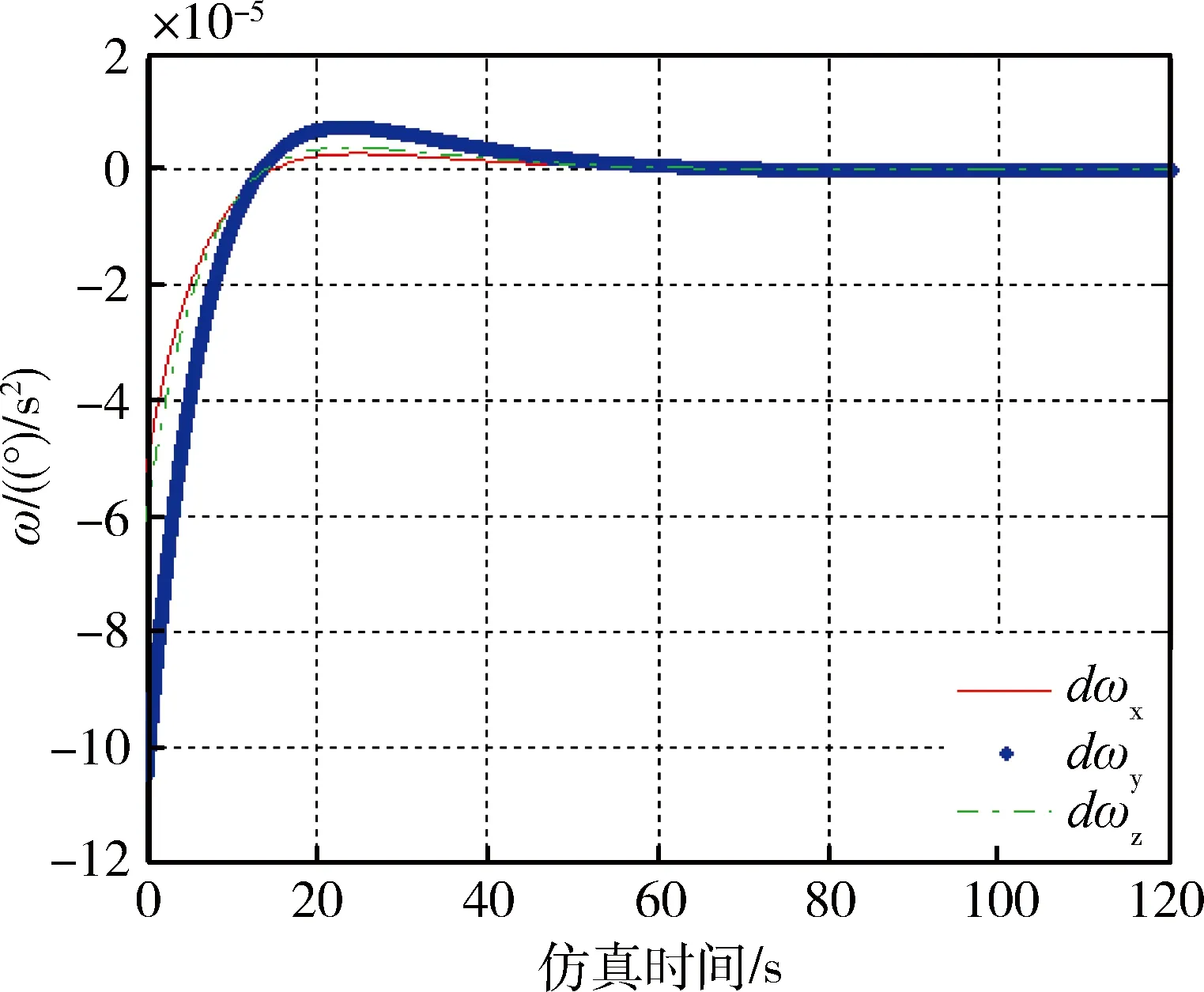
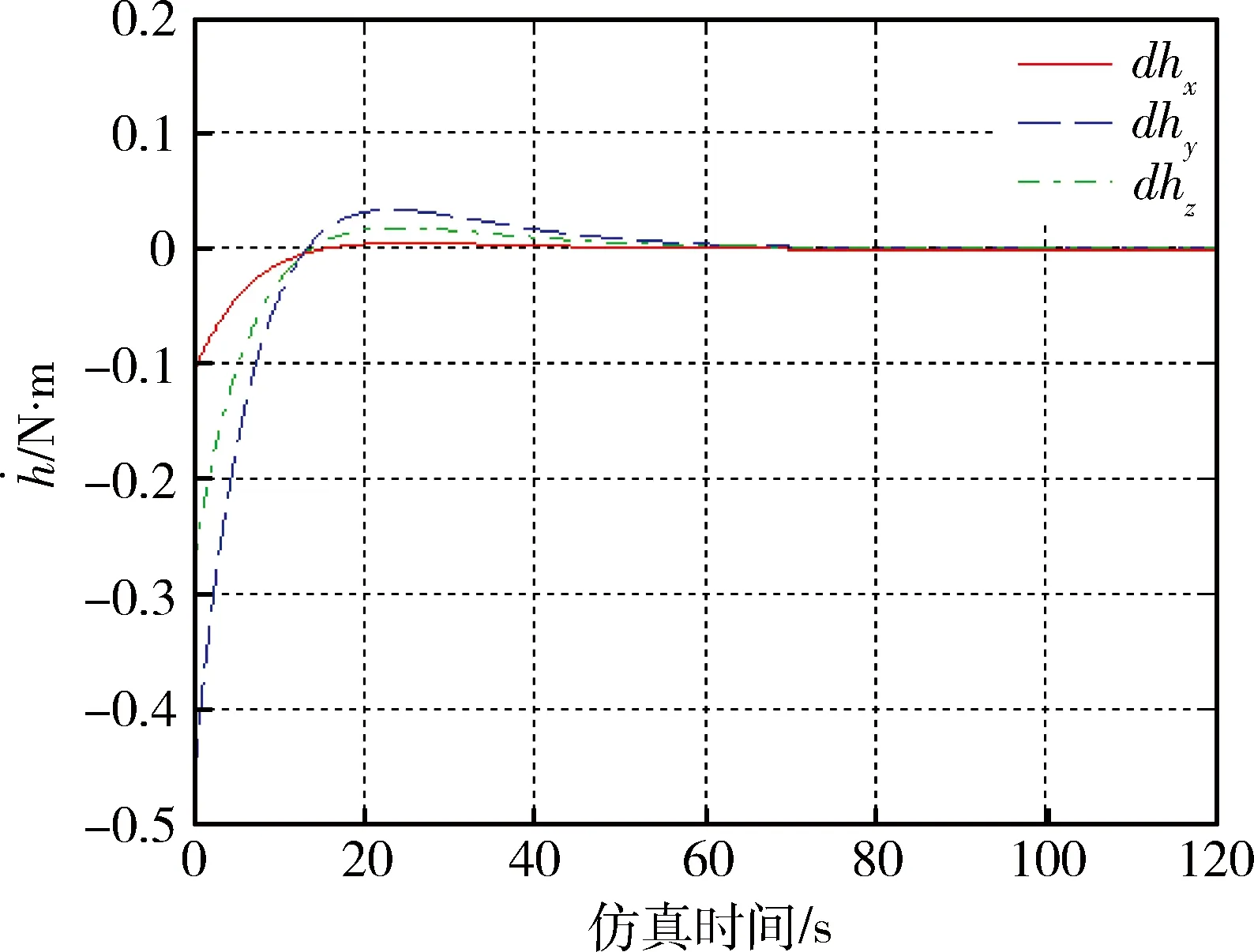
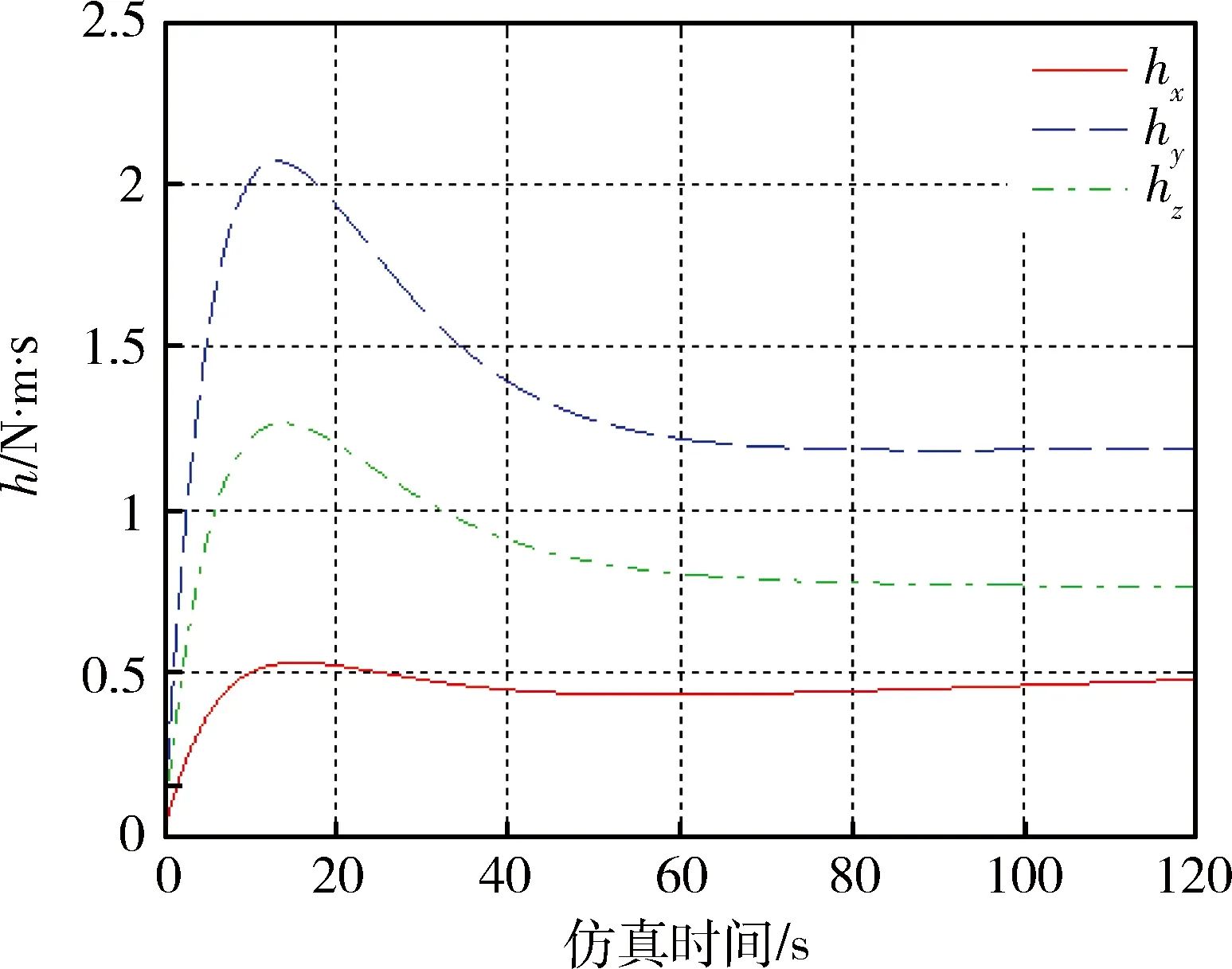
4 结 论

