基于自适应滤波的脉冲星导航方法研究*

褚永辉，李茂登，黄翔宇，王大轶

(1.北京控制工程研究所，北京 100190； 2.空间智能控制技术重点实验室，北京 100190)



基于自适应滤波的脉冲星导航方法研究*

褚永辉1,2，李茂登1,2，黄翔宇1,2，王大轶1,2

(1.北京控制工程研究所，北京 100190； 2.空间智能控制技术重点实验室，北京 100190)

基于X射线脉冲星的自主导航技术能够为深空探测航天器提供高精度导航信息.脉冲星星表误差对导航性能存在不利影响，特别是方差不确定的星表误差，会引起较大定位误差.建立不确定项的导航模型，提出一种基于方差匹配的自适应滤波方法，通过估计不确定观测模型中的待估参数减小不确定项对观测的影响.通过数学仿真对比了自适应滤波方法和传统扩展卡尔曼滤波方法(EKF)，验证了所提方法的有效性.

脉冲星导航；自适应卡尔曼滤波；自主导航

0 引 言

基于X射线的脉冲星导航技术是近些年来自主导航领域研究的热点方向，特别是对于深空探测领域，脉冲星导航具有高精度高自主等优点.脉冲星距离太阳系几万光年，且相对太阳系位置固定，可以为行星际乃至恒星际深空探测航天器提供导航信息.脉冲信号到达探测器的时间称为脉冲到达时间(TOA，time of arrival)，是脉冲星导航的基本观测量.利用X射线脉冲星导航的基本原理是：通过测量同一脉冲信号到达航天器和太阳系质心的时间之差可以确定航天器的位置、速度和时间等导航信息.

脉冲星导航依靠观测遥远的X射线脉冲信号获取观测量，因此不可避免地受到脉冲星星表误差影响.脉冲星角位置误差称为星表误差，主要指赤经赤纬误差，是影响脉冲星导航精度的重要因素.

文献[1]将星表误差看做常值偏差进行估计从而达到提高导航精度的目的，但是估计精度受导航精度制约；事实上，星表误差并不是常值，很多情况下表现为方差大小未知的不确定项.将星表误差看作是观测模型不确定项，利用先进滤波方法可以消除其不利影响.文献[2]使用鲁棒滤波方法对有界的方差进行了估计，提高了导航精度.但是在误差方差范围不确定时，一般采用基于方差匹配的自适应滤波方法[3-4].本文尝试采用自适应滤波方法克服星表误差的影响，特别是针对同时存在赤经赤纬两种星表误差时，提出一种基于方差匹配的自适应滤波方法(AKF，adaptive kalman filter).

首先介绍利用脉冲星(TOA)观测量实现航天器导航的方法，以及星表误差对导航精度的影响，并建立包含星表误差的观测模型；然后给出用于非线性不确定系统的自适应滤波方法；最后通过数学仿真比较了AKF与传统EKF算法，验证了所提方法的有效性.

1 基于脉冲星的航天器导航方法

1.1 轨道动力学模型

建立地外天体探测器的轨道动力学模型如下：

(1)

式中：rc为探测器在目标天体质心惯性系中位置矢量，rc=|rc|；vc为探测器在惯性系中速度矢量；μm为中心天体引力常数；F为除引力外作用于探测器的合推力；m为探测器质量；aε为天体非球形引力和第三体引力等引起的摄动加速度.

1.2 基于脉冲星测量的观测模型

脉冲星导航的原始观测量是X射线脉冲光子.当探测器检测到X射线波段能量范围的光子时，记录下光子的数量、能量和到达航天器的时间，然后将星钟记录的原子时转移到太阳系质心(SSB，solar system barycenter )处，得到太阳系质心坐标系下的光子到达时间序列.当观测一颗脉冲星时，该时间序列为标量.在太阳系质心坐标系下，考虑到相对论效应的影响和采用X射线探测器测量光子TOA的局限性，光子到达时间转换方程可以写成如下形式：

(2)

式中：tb表示脉冲光子到达SSB的时间；tsc表示同一光子到达航天器的时间；n表示SSB指向脉冲星的单位矢量，称为视线矢量；r表示航天器相对于SSB的位置；c表示光速；D0表示脉冲星到SSB的距离；b是SSB相对于太阳质心的位置矢量；μs是太阳引力常数；表示星钟漂移产生的偏差；vt表示测量噪声.本文暂不考虑星钟偏差δt影响.

(3)

通过长期天文观测得到的星历均存在误差，设赤经赤纬的误差分别为Δα和Δδ，则真实的星历可以写为

(4)

视线矢量n计算公式为

(5)

(6)

(7)

(8)

(9)

其中o[·]表示误差的高次项.忽略该高次项，将式(5)展开有

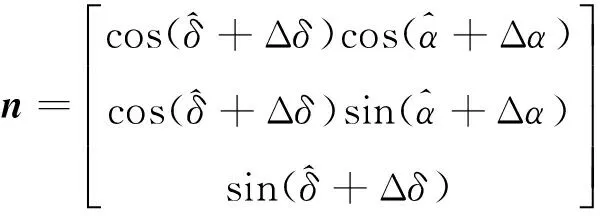
(10)

其中，Δn1和Δn2分别表示赤经误差Δα和赤纬误差Δδ对脉冲星方向矢量n的影响.具体可以表示为

(11)

(12)

这里，定义了变量矢量

(13)

星历误差对观测量的影响可以写为

(14)

该值大小与航天器位置成正比.对于太阳系中深空探测航天器，如果位置长度在1011m量级(地球附近)，那么对于0.001″的星表误差将大约造成10km量级的位置误差.而且该误差随航天器与SSB的距离增大而增大，因此必须设法消除其影响.

将式(12)和(13)代入到观测方程(3)即为

(15)

星表误差的值Δα和Δδ属于未知项，可以假设为方差未知的白噪声序列，并写为如下形式：

Δα=μvc，Δδ=λvc

(16)

其中μ>0，λ>0，表示方差调节参数；vc表示方差归一化后的白噪声序列，与测量噪声序列vt不相关，且有

(17)

因此观测方程(3)可以写为

(18)

式(18)即为含有不确定项的观测模型.对于确定的星历，ζ1和ζ2均为确定值，不确定项为μ和λ.可以将(ζ1μ+ζ2λ)·r看作整体作为待估参数设计相应的滤波算法进行估计.

2 基于方差匹配的自适应滤波方法

本文使用基于方差匹配的自适应滤波方法克服星表误差的不利影响.具体思路是利用时变参数描述带有不确定项的观测模型系统，根据该模型建立相应准则使得测量残差相互匹配，形成相应的自适应滤波方程.

考虑如下非线性系统：

(19)

离散形式的测量方程可以写为

z(k+1)=h(x(k+1))+v(k+1)

=h(x(k+1))+v1(k+1)+αv2(k+1)

(20)

其中，噪声v1为白噪声序列，有固定方差；v2为时变噪声序列，无固定方差，α≥0为可调节参数.假设两种噪声的方差不相关.

式(20)所示系统的测量残差可以写为

δz(k+1)=h(x(k+1))+

(21)

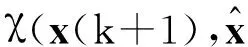
v1(k+1)+αv2(k+1)

(22)

因此式(22)所示的测量残差的协方差可以写为

H(k+1)P(k+1|k)HT(k+1)+

R1(k+1)+βR2(k+1)

(23)

其中

(24)

其中误差协方差矩阵P(k+1|k)可以表示为：

P(k+1|k)=

Φ(k+1,k)P(k|k)ΦT(k+1,k)+Qd

(25)

将式(25)代入式(23)有

S(k+1|k)=

H(k+1)P(k+1|k)HT(k+1)+

R1(k+1)+βR2(k+1)=

L1+βL2

(26)

式(26)中包含了测量残差信息，这里有定义

L2=R2(k+1)

(27)

通过N步测量可以求取测量残差的协方差均值

(28)

设计如下准则

(29)

(30)

结合传统的EKF滤波算法，得到自适应卡尔曼滤波器为

(31)

P(k+1|k)=

Φ(k+1,k)P(k|k)ΦT(k+1,k)+Qd

(32)

HT(k+1)+R1(k+1)

(33)

L2=R2(k+1)

(34)

(35)

(36)

S(k+1|k)=H(k+1)P(k+1|k)HT(k+1)+

R1(k+1)+βR2(k+1)

(37)

K(k+1)=P(k+1|k)HT(k+1)S-1(k+1|k)

(38)

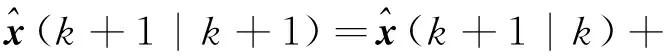
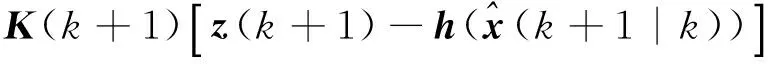
(39)

P(k+1|k+1)=

P(k+1|k)-K(k+1)H(k+1)P(k+1|k)

(40)

对于含有不确定模型的脉冲星导航系统，可以将(ζ1μ+ζ2λ)·r作为整体看作待估参数α利用以上公式进行估计.

3 数学仿真

图1 EKF估计误差Fig.1 Position error of EKF filter

图2 AKF估计误差Fig.2 Position error of AKF filter

图3 AKF和EKF估计误差比较Fig.3 Compare of AKF and EKF filter

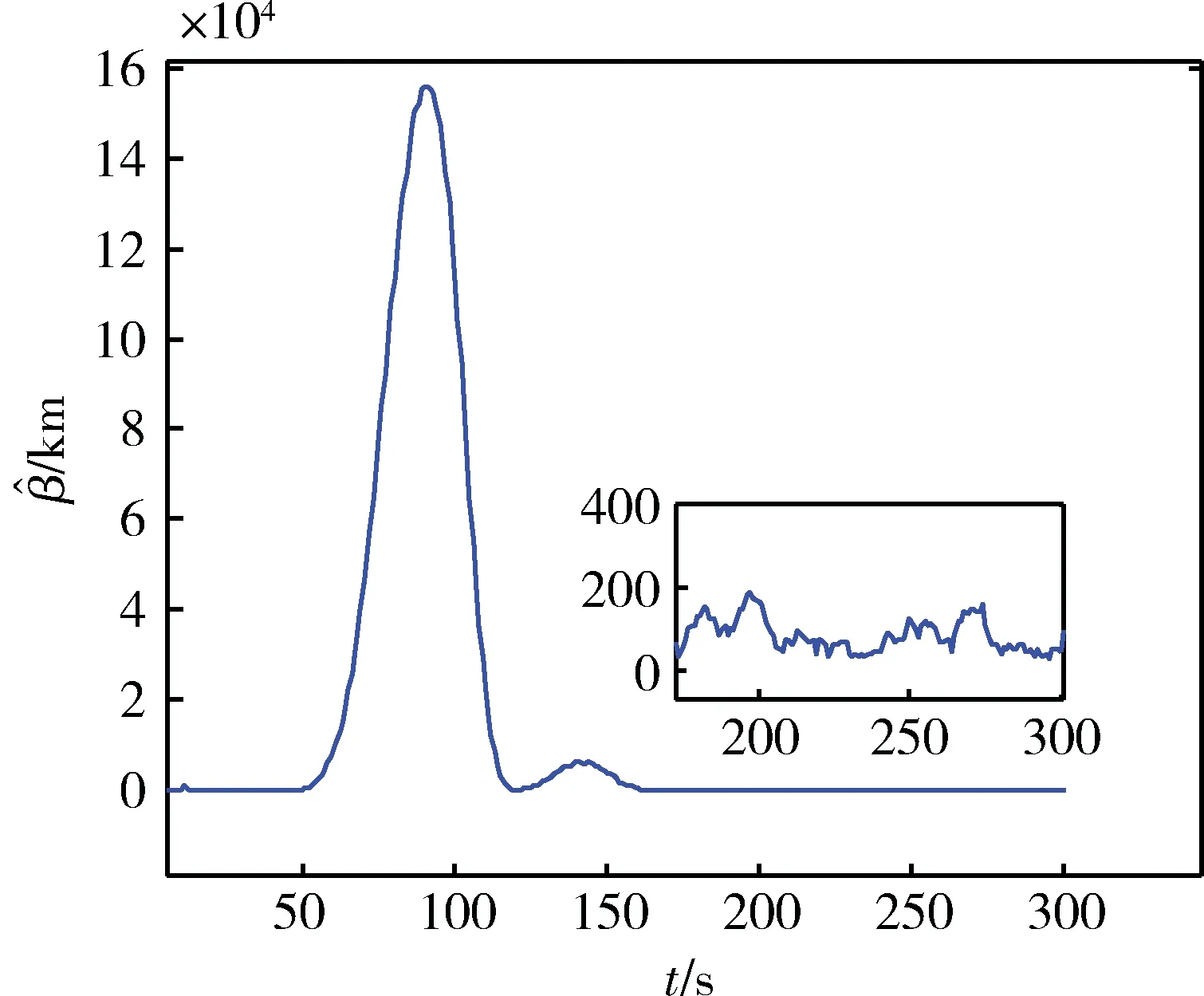
图估计值Fig.

4 结 论

本文研究了基于方差匹配自适应滤波的脉冲星导航方法，建立了带有星历误差影响的不确定观测模型，研究了可以用于脉冲星导航的自适应参数估计方法.仿真结果表明，基于方差匹配的自适应滤波方法是克服星表误差不确定性影响的有效手段，提高了导航精度.

[1] 孙守明, 郑伟, 汤国建. X射线脉冲星星表方位误差估计算法研究[J]. 飞行器测控学报, 2010, 29(2): 129. SUN S M, ZHENG W, TANG G J. A new estimation algorithm of the X-ray pulsar position error[J]. Journal of Spacecraft TT & C Technology, 2010, 29(2): 129.

[2] 熊凯, 魏春岭, 刘良栋. 鲁棒滤波技术在脉冲星导航中的应用[J]. 空间控制技术与应用, 2008, 34(6): 8-11. XIONG K, WEI C L, LIU L D. Application of robust filtering in pulsars-based navigation[J]. Aerospace Control and Application, 2008, 34(6): 8-11.

[3] MOHAMED A H, SCHWARZ K P. Adaptive Kalman filtering for INS/GPS[J]. Journal of Geodesy, 1999: 193-203.

[4] MYEONG J Y. INS/GPS integration system using adaptive filter for estimating measurement noise variance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1786-1792.

[5] HANSON J E. Principles of X-ray Navigation [D]. Stanford University： 450 Serra Mall, Stanford, CA, 1996.

Adaptive Filter of X-Ray Pulsar-Based Navigation

CHU Yonghui1,2, LI Maodeng1,2, HUANG Xiangyu1,2, WANG Dayi1,2

(1.Beijing Institute of Control Engineering， Beijing 100190， China； 2.Science and Technology on Space Intelligent Control Laboratory， Beijing 100190， China)

High-accuracy autonomous navigation information can be obtained autonomously by pulsar navigation, including the position, velocity, attitude and time. The precision of the pulsar navigation can be mainly affected by the pulsar’s position error system, especially the uncertainty variance affect. Firstly, the uncertainty model of the pulsar navigation is presented. Secondly, the adaptive filter can reduce the unacceptable effect uncertainty variance. Numerical simulation demonstrates the effectiveness of the proposed approach.

pulsar navigation； adaptive filter； autonomous navigation

*青年自然科学基金(61503023)和国家杰出青年科学基金项目资助(61525301)、民用航天项目资助项目.

2015-08-22

V488

A

1674-1579(2015)06-0008-05

10.3969/j.issn.1674-1579.2015.06.002

褚永辉(1983—)，男，工程师，研究方向为深空探测自主导航、制导与控制；李茂登(1985—)，男，高级工程师，研究方向为航天器导航、制导与控制；黄翔宇(1976—)，男，高级工程师，研究方向为航天器自主导航与制导；王大轶(1973—)，男，研究员，研究方向为深空探测航天器自主控制.