基于新的定位方法的空投技术研究*

魏 民，李小波，黄中瑞，唐文龙（电子工程学院，合肥 230037）

基于新的定位方法的空投技术研究*

魏 民，李小波，黄中瑞，唐文龙
（电子工程学院，合肥 230037）

针对空投技术的定位问题，提出了一种新的定位方法。首先，在空投目标区域放置发射机，发射天线在3个方向形成彼此相交的波束，发射机与3个波束的交点构成中心线，3个波束关于中心线对称。其次，发射天线在3个方向发射相同功率，不同频率的信号。最后，载荷上的接收机实时接收信号，经傅里叶变换得到信号频谱图。3个信号功率相等时载荷位于中心线上，保持现有飞行方向；3个信号功率不等时，根据偏离中心线的位置对飞行方向进行调整，确保载荷能够准确到达目标区域。该方法具有较高的定位精度，能够适应复杂电磁环境。

精确空投，中心线，重合度，航迹调整

0 引言

空投是指利用降落伞将人员和物资等投送到指定区域的一种技术，快捷和便于跨越复杂地形是其最突出的优点。在常规战争中空投技术经常被用作部队投送及弹药装备物资补给及部署的手段［1］；在冰雪灾害和“5·12”地震的救援中空投技术也发挥了重要的作用［2］。在传统的空投过程中，载荷离开运输机后无法对其运动进行操控只能使其在外力作用下自由降落，这导致其具有以下缺点。①空投系统受气象环境影响大，使得空投实际着陆点与预计目标点可能存在较大的偏差；②投放精度受空投高度和空投区域风场的影响比较大，载荷的落地点散布较大；③空投运输机不得不飞临空投区域很近的地方进行空投，这增加了空投飞机自身的危险性。

针对传统空投的不足，文献［3］提出了精确空投的概念，精确空投将导航制导和先进控制技术融入空投系统，即载荷离开运输机后可控制运动轨迹，实现高精度空投。文献［4-5］介绍了精确空投系统的优势，并对系统上装置的发展趋势进行了研究。文献［6-10］介绍了国外先进的精确空投技术，包括AGAS可承受制导空投系统，GDS普通投送系统，“尖叫者”快递投送系统等等，这些精确空投系统都采用了GPS定位系统进行导航，精度较高，但存在两点不足。1）在比较复杂的电磁环境下，接收不到足够的GPS信号以实现精确定位；2）由于GPS完全由美国政府控制和运营，一旦国家出现紧急情况，美国政府可以关闭GPS，仅供美国军方使用。

针对使用GPS精确空投系统存在的不足，本文提出了一种新的定位方法并应用到空投技术。该方法在保持较高精度的同时，克服基于GPS定位的不足，能够在复杂的电磁环境下工作，应用范围较广。

1 基本原理

1.1 新的定位方法的模型

基本思想:首先，在空投目标区域放置一个发射机，发射天线在3个不同方向形成彼此相交的波束，发射机与3个波束的交点构成中心线，3个波束关于中心线对称。其次，发射天线在3个方向发射相同功率，不同频率的信号。最后，载荷上的接收机实时接收信号，经傅里叶变换得到信号频谱图。3个信号功率相等时载荷位于中心线上，保持现有飞行方向；3个信号功率不等时，根据偏离中心线的位置对飞行方向进行调整，确保载荷能够准确到达目标区域。

建立模型:假设发射天线方向图函数为高斯函数，3个方向上的增益函数分别为G1（θ，φ），G2（θ，φ），G3（θ，φ）。θ，φ分别表示俯仰角和方位角，合理选择3个波束的指向使它们彼此相交，并且关于中心线对称。3个基带信号发射功率Pt，频率分别为f1、f2和f3，调制载频为fc。载荷上宽接收波束增益为固定值G2，R是载荷接收机与发射机的距离。接收机实时接收信号，经解调、滤波后得到

式（1）中y1（t）、y2（t）、y3（t）表示最终接收到的混合信号，s1（t）、s2（t）、s3（t）为接收的纯净信号，n1（t）、n2（t）、n3（t）表示接收机噪声。

根据式（2）求得信号功率为Pr1，Pr2，Pr3。混合信号的功率分别为P1，P2，P3，由式（3）求解得到。

其中式（3）中的NN是时间上的离散点个数。Pr1，Pr2，Pr3，P1，P2，P3是M×N维矩阵，M和N分别是方位角和俯仰角的离散点个数。

若某一方位角φ0，俯仰角θ0使得P1（θ0，φ0），P2（θ0，φ0），P3（θ0，φ0）相等，（θ0，φ0）就是中心线的方向。下面给出一种循环算法求解中心线位置，模型为:

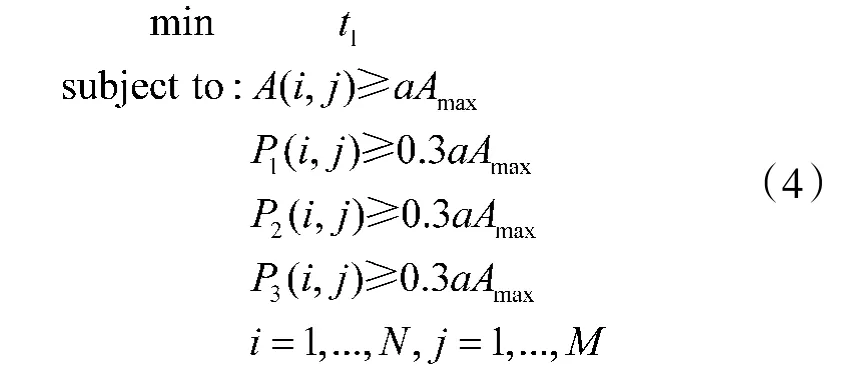
其中，A=P1+P2+P3是将方位和俯仰离散后得到总的功率矩阵。a是门限倍数，a的取值小于1，Amax表示矩阵A中的最大值，将aAmax作为检测门限，目标函数t由式（5）求得

基本思想是:当3个混合信号功率越接近，目标函数的值就越小，当目标函数最小时对应的方位和俯仰就是要求解的中心线位置。如果在空间某些位置接收到的信号功率小于噪声功率，噪声对算法影响非常大，约束条件A（i，j）≥aAmax可解决这个问题，只有满足条件的值，才可以用于目标函数的求解。其余的约束条件可避免3个混合信号功率相差太大，造成较大的计算误差。

如果经过上面的计算结果并不唯一，在满足式（5）的前提下，将多个计算值代入式（6），使其最小的计算值就是最终的结果。

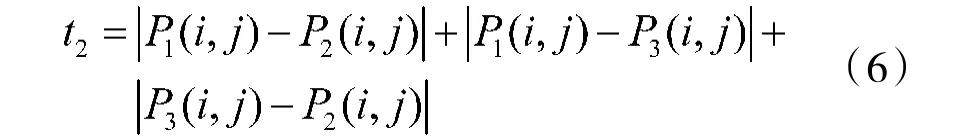
1.2 精确空投的工作过程

精确空投作业工作流程图如图1所示。

图1 精确空投工作流程图

运输机在起飞之前，根据所要投放目标区域及其周围的环境，运用计算机建模的方式初步计算投放点的位置，并将数据传递给飞行员。当飞机抵达计算空投点之后，在投放前将规划轨道（即标准轨道）、当前位置信息和环境等信息上传到精确空投系统单元上。投放之后，飞机与精确空投系统不再进行通信，由于环境因素可能导致载荷偏离理想路径。利用文中所给出的定位算法，3个信号功率相等时载荷位于中心线上，保持现有飞行方向；3个信号功率不等时，根据偏离中心线的位置对飞行方向进行调整，确保载荷能够准确到达目标区域。

2 仿真实验

2.1 发射波束的形成

图2 3个波束在空间上的方向图

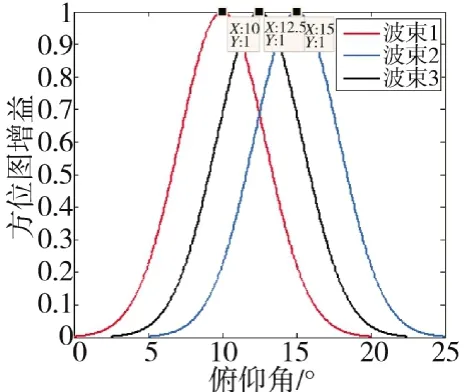
图3 3个波束在俯仰上的方向图

图2和图3分别给出了波束在空间和俯仰上的方向图，仿真结果表明了设计方案的正确性。该方法的优点是能够改变增益最大值的俯仰角和方位角，得到不同指向的3个波束。

在这里对波束的重合度进行定义，重合度是指中心线位置的功率与最大功率的比值，即归一化方向图中心线位置数值，将代入方向图函数，得到此时的重合度为0.606 5。

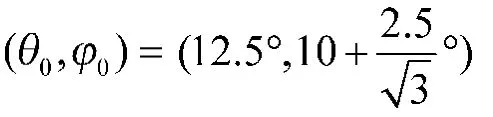
2.2 定位精度随信噪比的变化

首先，对信噪比和误差进行定义。由于载荷上接收机接收的3个信号的功率不同，如果采用传统的定义方法，同一位置将出现3个不同的信噪比。因此，定义信噪比为接收机能够接收到的最大信号功率与噪声功率的比值。

仿真条件:假设雷达发射信号为线性调频信号，发射功率Pt=0.32 mW，调制频率fc=3 GHz，基带信号中心频率f1=10 MHz，f2=15 MHz，f3=20 MHz，信号带宽B=25 MHz，接收机通频带宽Bn=25 MHz，方位角度为0∶360°，俯仰角度0∶180°，方位离散点数M=5 000，俯仰离散点数N=5 000，时间离散点数NN=200，3个波束参数设置与2.1节相同，发射天线增益最大值Gmax=20 dB，接收天线增益G2=20 dB，目标点与载荷之间的距离R为0∶1 km，实验次数MM=200，采用第2节给出的模型，并定义误差为，得到平均误差与信噪比关系如图4所示。

图4 精度随信噪比变化图

图4给出了门限倍数为0.5，重合度0.606 5时，测量误差随信噪比变化的关系，从图可以看出随着信噪比的逐渐增大，误差逐渐减小，并且在信噪比为17 dB时，测量误差处于稳定状态，不再随信噪比增大而减小。这是因为信噪比较大时，接收机通道噪声功率相对于信号功率非常小，基本可以忽略不计。当信噪比较大时，该方法精度较高，可以将误差控制在0.1°以下。

2.3 门限倍数与信噪比的关系

本节将简要分析利用第2节提出的模型进行计算时，在不同的信噪比下，对门限倍数的最低要求。最低要求表示如果门限倍数再降低，模型将失效。仿真条件与2.2节一样，最低门限倍数仿真结果如下页图5所示。

图5给出了重合度为0.606 5时，最小门限倍数随信噪比的变化关系，从图可知，随着信噪比逐渐增大，最小门限倍数逐渐减小，即对门限倍数的要求变松。这是因为信噪比较小时，接收机噪声对混合信号功率的影响较大，此时必须提高门限倍数以降低噪声的影响，随着信噪比的增大，接收机噪声对混合信号功率的影响变小，门限倍数降低并不影响最终结果。因此，可以使用较大的门限，使得在载荷飞行的整个过程，模型都不会失效，在本文中取门限倍数a=0.5。

图5 最小门限倍数随信噪比变化图

图6 精度随重合度变化图

2.4 定位精度随重合度的变化

本节将在门限倍数为和信噪比为确定情况下，讨论重合度对计算精度的影响。通过改变（θ1，φ1），（θ2，φ2），（θ3，φ3），改变重合度大小，但始终保持中心线的位置为

图6给出了门限倍数为0.5，信噪比分别为5.23 dB，6.99 dB，10 dB情况下，计算精度随重合度变化曲线。从图中可以看出，在信噪比一定的情况下，当重合度较小时，随着重合度的逐渐增大，精度也逐渐提高；当重合度增加到一定大小时，随着重合度的增加，精度反而变差。这是因为重合度较小时，接收机在中心线位置接收到的信号较弱，噪声对精度影响较大；当重合度太大时，接收机在中心线位置接收到的信号较强，稍微偏离中心线，接收到的3个信号功率相差很小，导致精度也不高。仿真结果表示，重合度不能太大，也不能太小。从图中可以看出，不同的信噪比下，精度随重合度的变化曲线也不相同，信噪比越大，最佳重合度越小，这是因为信噪比较大时，噪声影响较小，较小的重合度就可以满足精度要求。从上述分析可知，当载荷距离目标区域较远时，选取较大的重合度，随着载荷离目标区域越来越近，可以逐渐降低重合度，始终保证较高的精度。

3 结论

本文提出了一种新的定位方法，并将其应用到空投技术。该方法克服GPS方法的不足，适用范围较广。在空投目标区域放置发射机，发射天线在3个方向形成彼此相交的波束，发射机与3个波束的交点构成中心线，3个波束关于中心线对称。发射天线在3个方向发射相同功率，不同频率的信号。载荷上的接收机实时接收信号，经傅里叶变换得到信号频谱图。3个信号功率相等时载荷位于中心线上，保持现有飞行方向；3个信号功率不等时，根据偏离中心线的位置对飞行方向进行调整，确保载荷能够准确到达目标区域。文中给出了计算模型，通过分析信噪比对精度的影响，可以看出该方法在信噪比较低的情况下，精度依然较高，具有较强的实用价值；通过对门限倍数的分析，选取了合适的门限倍数确保计算方法不失效；通过分析重合度对精度的影响，可知通过改变重合度大小，使得载荷飞行过程中计算方法始终保持较高的精度。该方法不仅可以用于空投技术，还可以用于联合寻敌，装备对接等多个领域。

［1］于成果，李良春.精确空投系统分析［J］.兵工自动化，2007，26（4）:L06-L07.

［2］蒲志刚，李良春，唐波.基于应急突发事件的精确空投保障［J］.科技广场，2009，22（9）:53-56.

［3］BENNEY R，BARBER J，MCGRATH J，et al.The joint precision airdrop system advanced concept technology demonstration［C］//AIAA 2005-1601 Aerodynamic Decelerators Conference，Munich，Germany，2005.

［4］于成果.精确空投系统轨迹的预测与规划［D］.石家庄:军械工程学院，2008.

［5］韩雅慧，杨春信，肖华军，等.翼伞精确空投系统关键技术和发展趋势［J］.兵工自动化，2012，31（7）:1-7.

［6］赵福英.从“天女散花”到“定点投送”——高空精确空投技术的最新发展［J］.现代兵器，2005（5）:18-21.

［7］BROWN G，HAGGARD R.The affordable guided airdrop system （AGAS）［C］//CEAS/AIAA 15th Aerodynamic Decelerator Systems Technology Conference，AIAA Reston，VA，1999.

［8］邹辉.精确空投系统的发展［J］.现代军事，2006，32（11）: 90-92.

［9］JENNY M S，CHRIS M M，ALAN L S.An overview of the guided parafoil system derived form X-38 Experience［J］. 2005.

［10］HATTIS P，FILL T，RUBENSTEIN D，et al.An advanced on-board airdrop planner to facilitate precision payload delivery［J］.AIAA Paper，2000，43（7）:52-54.

A Study on Airdrop Technology Based on New Positioning Method

WEI Min，LI Xiao-bo，HUANG Zhong-rui，TANG Wen-long
（Electronic Engineering Institution，Hefei 230037，China）

Aiming at the positioning problem of airdrop technology，this paper proposes a new positioning method.Firstly，a transmitter is placed in airdrop target area，and transmitting antenna forms three beams intersecting with each other in three directions.The transmitter and three beams intersection forms the center line and three beams is symmetric.Further，transmitting antenna launches signals with the same power and different frequency in three directions.Finally，receiver on the load receives the signals and we can get the signal spectrum by Fouier transformation.When the power of three signal is equal，the load is located at the center line and keeping the current flight direction. When the power of three signal is unequal，the flight direction is adjusted according to the position of the center line and the load can reach to the target area accurately.This method has higher accuracy and can be adapted to complex electromagnetic environment.

precise airdrop，center line，coincidence degree，track adjustment

TN966

A

1002-0640（2017）03-0041-04

2016-01-17

2016-02-25

国家自然科学基金（61272333）； 安徽省自然科学基金资助项目（1308085QF99）

魏 民（1993- ），男，河南驻马店人，硕士研究生。研究方向：空时自适应处理，雷达信号处理。