强降雨作用下软弱夹下卧层边坡稳定分析
王 立 刚
(中铁二十四局集团轨道交通分公司,上海 200070)
强降雨作用下软弱夹下卧层边坡稳定分析
王 立 刚
(中铁二十四局集团轨道交通分公司,上海 200070)
采用大型非线性有限元软件ABAQUS,基于饱和—非饱和渗流理论,建立了强降雨条件下非饱和夹软弱土层土坡稳定性分析有限元模型,并结合实例,研究了雨水入渗的瞬态渗流对应力与位移的影响,并分析了边坡的稳定性,可以为强降雨条件下夹软弱土层边坡稳定性评价及工程预防提供参考。
软弱土层,边坡,强降雨,稳定性
0 引言
软土在我国分布很广,具有抗剪强度低、孔隙比大、渗透系数很小以及压缩性高等特点,特别是在我国东南沿海一带,加之特大暴雨、强台风等极端天气频繁,各种滑坡灾害屡见不鲜,从而促使国内外很多专家学者对强降雨条件下边坡稳定性分析和安全性评价进行了研究[1-10]。降雨入渗是引发边坡失稳破坏的主要因素,沈水进等[11-13]对雨水冲刷—渗透过程对非饱和边坡作用机制做了进一步探究,并建立了降雨入渗物理模型试验;对于非饱和软土渗流问题中的材料模型,王立忠等[14]在室内试验基础上得到了结构性软土切线泊松比的计算式,初步解决了在应用非线弹性模型时的泊松比取值问题,吕卫清等[15]从固结系数定义出发,利用试验数据提出了渗透系数与固结应力关系式;在数值模拟分析方面,毛畅熙等[16]基于饱和—非饱和渗流理论,采用极限平衡和强度折减有限元方法探讨了降雨入渗对边坡稳定性的影响。然而,实际工程中的边坡不同于自然边坡,不仅常年暴露于自然环境中,承受自然条件和人类活动的影响,而且其经过多层压实,边坡失稳原因极其复杂,对于下夹软弱土层边坡更是如此。目前针对夹软弱土层边坡稳定性分析的文献还较少,如何综合考虑含有两种材料参数建立模型,以及土体含水量增加和抗剪强度减弱对边坡稳定性的影响是本文的研究重点。
降雨入渗是一种典型的非饱和流固耦合现象,因此本文基于饱和—非饱和渗流理论,采用弹塑性有限元模型,并考虑降雨入渗过程中含水量增加、强度软化和渗透力增大等因素的影响,建立强降雨作用下夹软弱土层边坡有限元模型。结合经典实例,考虑渗流场和应力场之间的耦合作用对土坡进行稳定性分析,验证所建模型的可靠性,以期为强降雨条件下夹软弱层土边坡稳定分析和采取工程预警措施提供设计理论基础。
1 降雨入渗非饱和土坡模型建立
1.1 渗流基本方程
非饱和非稳定渗流土坡稳定性分析关键是土坡内非稳定渗流场的计算,考虑一个非饱和土体单元,基于非饱和土Darcy定律和质量守恒原理,得到饱和—非饱和渗流基本方程[3]为:
(1)
其中,n为孔隙率;Sr为饱和度;ευ为土骨架体应变;kwij为渗透系数;ρw为水密度;uw,j为孔压;bj为单位体积力。
(2)
(3)
对式(3)采用伽辽金加权余量法求解可得到有限元方程。
1.2 入渗边界条件
降雨入渗过程十分复杂,入渗量与降雨强度q、土壤允许入渗的容量fp、土壤饱和时水力传导系数kws以及降雨持续时间等因素有关。可采用Mein-Larson模型考虑降雨入渗边界条件:
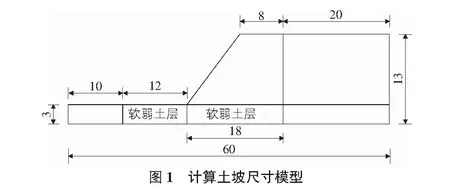
1)q 2)fp>q>kws:降雨全部入渗,但降雨量还未达到fp,且fp逐渐降低; 3)q>fp:部分降雨不入渗,形成地表径流,坡面土体基本处于饱和。 本文采用第2)种情况。 1.3 非饱和渗流水力特性 非饱和非稳定渗流水力特性很难通过理论方法求出,目前主要通过试验手段来确定。常用模型很多,本文采用1977年弗雷德隆提出的Van Genuchten[17]模型: 1.4 饱和—非饱和渗流有限元解法 假设单元体基函数Ni由M个结点坐标构成,则单元体内任意一点水头函数为: (4) 根据有限元和变分原理,渗流有限元计算式可表示成: [H]{h}={F} (5) 其中,[H]为渗流矩阵;{h}为结点水头矩阵;{F}为结点流量矩阵。 根据边界条件,结合式(4)和式(5)可求得各结点水头值,从而完成整个渗流场的求解。 2.1 计算模型与参数 为了研究非饱和非稳定渗流对夹软弱土层边坡稳定性的影响,引用费康等[18]给出的如图1所示的夹软弱土层土坡作为算例。该土坡坡高10 m,基地厚3 m,坡角β=45°,软弱土层如图1中所示,初始水位位于坡脚水平面。采用四节点平面应变双线性孔压四边形单元划分计算网格见图2,底部水平边界约束水平、竖向位移,左右两侧竖向边界约束水平位移,共883个节点,791个单元。采用Mohr-Coulomb弹塑性本构模型,平均降雨强度设为18 mm/h,计算连续降雨96 h后边坡在任意时刻任意结点应力、位移以及瞬态渗流场,计算参数见表1,降雨强度随时间变化幅值见表2。 材料名称弹性模量MPa泊松比干密度kg/m3粘聚力kPa摩擦角(°)饱和渗透系数mm/h坡体100.31300203018软土5.70.457507.219.10.019 表2 时间和幅值大小关系 2.2 边坡降雨入渗分析 初始水头边界设为坡脚水平面处,孔压等值线分布云图见图3。降雨24 h,48 h,72 h和96 h后的降雨入渗后的孔压分布图与初始状态差别很大,随着降雨时间增加,边坡上部土层含水量上升,基质吸力有所减小。若将孔压等于零处在云图中显示出来,还可清晰地看到任意时刻浸润面的位置,从而判断水流入渗情况。在到72 h降雨减小或停止后,孔隙水压力也将有所减小,饱和度减小,土体浅层基质吸力逐渐增加。 2.3 边坡降雨稳定性分析 在降雨入渗分析之前,需要知道初始应力、初始饱和度等初始条件。本文首先采用线弹性模型进行了一个静水位分析,得到了一系列初始状态,其中,初始竖向有效应力分布如图4所示。由图4可见,在土坡顶部竖向有效应力不为零,这是因为在ABAQUS中,有效应力: σ′=σ-(χuw+(1-χ)ua)。 该式反映了基质吸力的影响,将χ取为饱和度Sr,ua取为0,则σ′=σ-Sruw。 降雨24 h,48 h,72 h和96 h后的有效应力:土坡体中竖向有效应力成层分布,且随深度逐渐增加。在到72 h降雨强度未减弱之前,有效应力随时间增加逐渐减小,72 h之后,伴随着降雨强度减弱甚至停止时,竖向有效应力随时间呈增长趋势。 本例中初始时刻应变量为零,降雨24 h,48 h,72 h和96 h后的有效应变:随时间增加有效应变逐渐减小。降雨一开始,软土层区应变比较剧烈,直到降雨72 h后和其他层区具有相同有效应变。在降雨72 h强度减弱或停止后可以看到,有效应变有增加趋势,这是因为降雨强度减小,孔隙水压力逐渐减小,基质吸力又逐渐增加,土体内有效应力增加。 从数值模拟结果中可以看出,降雨入渗作用下塑性区首先出现在坡脚浅层,沿着坡面向上发展,与实际工程中滑塌现象一致。该实例较好的验证了强降雨条件下夹软弱土层边坡稳定性分析有限元模型的可靠性,可以为该工况下土坡稳定性评价及工程预防提供技术思路与参考。 本文重点研究了强降雨条件下非饱和非稳定渗流对夹软弱土层边坡的入渗及稳定性分析,基于饱和—非饱和理论,考虑软土材料特性,建立了有限元分析模型。通过算例分析,得出了一些结论:1)降雨入渗之前,坡体基本处于稳定状态;2)持续降雨一段时间,降雨强度未减弱之前,土坡上部土层含水量增加,饱和度增大,基质吸力减小或消失,坡脚处开始出现塑性应变;3)降雨强度减小或停止后,坡体内孔隙水压力又逐渐减小,饱和度减小,基质吸力逐渐回升,有效应力和有效应变有增加趋势。 软土具有渗透系数小、抗剪强度低和压缩性高等特点,其材料参数随土层不同变化很大,所以软土边坡稳定性分析应该是进一步研究的方向,本文仅为强降雨条件下夹软弱土层边坡稳定分析提供一般思路和参考。 [1] 魏 宁,茜平一,傅旭东.降雨和蒸发对土质边坡稳定性的影响[J].岩土力学,2006,27(5):778-782. [2] 吴李泉,张 锋,凌贤长,等.强降雨条件下浙江武义平头村山体高边坡稳定性分析[J].岩石力学与工程学报,2009,28(6):1193-1199. [3] 贾苍琴,黄茂松,王贵和.非饱和非稳定渗流作用下土坡稳定分析的强度折减有限元方法[J].岩石力学与工程学报,2007,26(6):1290-1296. [4] 祝小靓.流固耦合下的土石坝稳定性分析研究[D].南昌:南昌大学硕士学位论文,2011:16-26. [5] 黄茂松,贾苍琴.考虑非饱和非稳定渗流的土坡稳定分析[J].岩土工程学报,2006,28(2):202-206. [6] 王 栋,年廷凯,陈煜淼.边坡稳定有限元分析中的三个问题[J].岩土力学,2007,28(11):2309-2318. [7] CHEN H,LEE C F,LAW K T.Causative mechanisms of rainfall-induced fill slope failures[J].Journal of Geotechnical and Geoenvironmental Engineering,2004,130(6):593-602. [8] ZHAN T L T,NG C W W.Analytical analysis of rainfall infiltration mechanism in unsaturated soils[J].International Journal of Geomechanics,2004,4(4):273-284. [9] 徐 晗,朱以文,蔡元奇,等.降雨入渗条件下非饱和土边坡稳定分析[J].岩土力学,2005,26(12):1957-1962. [10] 李兆平,张 弥.考虑降雨入渗影响的非饱和土边坡瞬态安全系数研究[J].土木工程学报,2001,34(5):57-61. [11] 沈水进,孙红月,尚岳全,等.降雨作用下路堤边坡的冲刷—渗透耦合分析[J].岩石力学与工程学报,2011,30(12):2456-2462. [12] TOHARI A,NISHIGAKI M,KOMATSU M.Laboratory rainfall-induced slope failure with moisture content measurement[J].Journal of Geotechnical and Geoenvironmental Engineering,2007,133(5):575-587. [13] ZHANG J,JIAO J J,YANG J.In-situ rainfall infiltration studies at a hillside in Hubei Province,China[J].Engineering Geology,2000,57(1/2):31-38. [14] 王立忠,李玲玲.结构性软土非线弹性模型中泊松比取的值[J].水力学报,2006,37(2):150-159. [15] 吕卫清,董志良,陈平山,等.正常固结软土渗透系数与固结应力关系研究[J].岩土力学,2009,30(3):769-773. [16] 毛畅熙,段祥宝,李祖贻,等.渗流数值计算与程序应用[M].南京:河海大学出版社,1999. [17] Forsyth P.A.Comparison of the single-phase and two-phase numerical model formulation for saturated-unsaturated groundwater flow[J].Computer Methods APPI,Mech,Engrg,1988(5):243-259. [18] 费 康,张建伟.ABAQUS在岩土工程中的应用[M].北京:中国水利水电出版社,2010. 文章编号:1009-6825(2017)05-0095-02 Stability analysis of slope with soft underlying layer under heavy rainfall action Wang Ligang (RailTransportationBranch,ChinaRailway24thBureauGroupCo.,Ltd,Shanghai200070,China) Using large-scale non-linear finite element software ABAQUS, based on the theore of saturated-unsaturated seepage, the finite element model of stability of unsaturated slope with soft soil layer under the condition of heavy rainfall is established. Combined with example, the transient seepage of the rain infiltration influence on stress and displacement are simulated, and the stability of this slope is analyzed, and can be placed for reference under the condition of heavy rainfall of the soft soil slope stability evaluation and engineering prevention are provided. soft soil layer, slope, heavy rainfall, stability 1009-6825(2017)05-0092-03 2016-12-04 王立刚(1983- ),男,工程师 TU413.62 A
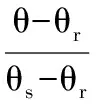
2 算例及分析




3 结语

