明框式铝合金玻璃幕墙动力响应分析★
傅蜀燕 黄海燕 杨立凡
(云南农业大学水利学院,云南 昆明 650201)
明框式铝合金玻璃幕墙动力响应分析★
傅蜀燕 黄海燕 杨立凡
(云南农业大学水利学院,云南 昆明 650201)
采用Davenport风速谱,编制了MATLAB计算程序模拟脉动风速时程,并根据规范转换为脉动风荷载,据此建立了时程分析流程,通过分块Lanczos方法进行了模态分析,同时计算了玻璃幕墙的瞬态响应,计算结果可为实际工程设计提供参考。
玻璃幕墙,风荷载,模态分析,时程分析
0 引言
铝合金玻璃幕墙作为一种新型轻围护构件,被广泛应用于各种建筑中。幕墙属于建筑上非承重的外围结构,风荷载是其最主要承受的荷载,且玻璃幕墙在大风中破坏时,极易对人造成伤害。在迎风面,气流遇到建筑物的阻挡,就形成高压气幕作用在玻璃幕墙上。在背风面,建筑物两侧产生涡旋会对建筑物产生吸力,该吸力作用在玻璃幕墙上。由于风随建筑物的体形、高度、面积的变化,风速和风向也不断改变,因此玻璃幕墙在风载作用下的问题属于动力学问题。
1 工程概况
某玻璃幕墙结构属于单元明框式铝合金玻璃幕墙,结构高度为10 m,宽4.1 m,受力体系是由铝合金横框和竖框组合而成,恒载主要为结构构件的自重,铝合金型材截面为100 mm×25 mm,壁厚1 mm。玻璃为4 mm厚钢化玻璃,尺寸为1 400 mm×1 000 mm。
在计算过程中,假定玻璃与铝合金框架为一个整体,墙体对铝合金玻璃幕墙四周边框的约束近似认为固定约束。
2 脉动风速时程
自然界的风由平动风和脉动风构成,脉动风的强度随时间按随机规律变化。幕墙的抗风受力可认为是在脉动风沿顺风向作用。国内外学者通常采用风洞试验的风压时程或计算机模拟的风压时程作用于结构计算模型上,通过动力计算得到结构的位移、应力与时间的关系[1,2]。在没有风洞实验的条件下,采用数值模拟获得风荷载风速时程是行之有效的办法。
2.1 脉动风速功率谱
风的模拟在实际工程中使用最广泛的方法大体分为两类:谐波叠加法和线性滤波法。本文采用湍流尺度沿高度不变的Davenport风速谱[3],其表达式为:
(1)
(2)
式中:n——脉动风频率;v*——流动剪切速度;v10——10 m高度处的平均风速;K——与地貌有关的常系数。
2.2 脉动风的空间相关性
由于空间各位置的风速、风向并不是完全同步,甚至可能是完全无关的,因此对于迎风面尺度较大的结构须考虑脉动风的空间相关性。相干系数采用Davenport给出的经验公式[5]:

(3)
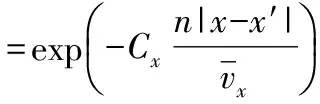
(4)
其中,ρz,ρx分别为垂直和水平方向脉动风压的相干函数;z-z′,x-x′分别为垂直和水平方向两点间的距离;Cz和Cx的值Davenport建议取Cz=7,Cx=8。
2.3 线性滤波法风速时程
线性滤波法中的AR模型[6,7]和ARMA模型能输出为具有指定谱特征的随机过程。在进行风速时程模拟时,各个参数的选取常决定着模拟精度、计算速度及程序能否运行等情况,因此参数的合理选择尤为重要。时间步长建议不小于0.1 s。通常采用低阶的自回归模型即可较好的模拟随机过程,一般取5阶即可得到较精确的结果,模拟参数如表1所示。

表1 脉动风速模拟主要参数
采用Davenport风速谱,以10 m高的平均风速为参考风速,编制MATLAB程序模拟脉动风速时程,如图1所示。并对脉动风速时程样本的功率谱进行检验,如图2所示。

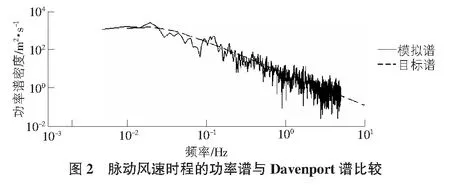
从图2可以看出,模拟得到的功率谱密度函数图形与目标功率谱具有良好的吻合性,说明本文中使用的线性滤波法编制的MATLAB程序可以较好地反映实际风速的脉动特性,且具有相当高的精度。
3 玻璃幕墙的动力分析
3.1 有限元模型
横、竖铝合金框采用Beam189单元,该单元考虑了剪切变形效应。玻璃幕墙采用Shell63单元。材料主要参数如表2所示。如图3所示的有限元模型共有3 247个节点和1 846个单元。

表2 材料性能参数
3.2 模态分析
采用分块Lanczos法进行模态分析,并提取前3阶振型。其固有频率和振动特性如表3所示,前3阶模态如图4所示。

表3 铝合金玻璃幕墙结构的前3阶固有频率和振动特性

阶数固有频率振型特性10.541E-02弯曲振动20.148E-01扭转振动30.15E-01弯曲振动
从图4中可以看出,第1阶模态振型是幕墙在Z轴振动,表现为绕X轴的弯曲振动;第2阶模态振型是幕墙绕Y轴扭转振动,表现为幕墙两侧竖框带动幕墙绕Y轴的扭转振动;第3阶模态振型是幕墙在Z轴振动,表现为上下两侧绕X轴的弯曲振动。
3.3 时间历程分析
大气的湍流使风速具有明显的紊乱性和随机性。因此,分析类型为瞬态分析,求解方法采用模态叠加法。根据规范[8,9],将数值模拟的风荷载时程转换为结构上的脉动风荷载,并利用APDL语言将脉动风荷载数据导入时程分析的循环计算中,具体流程如图5所示。在进行风荷载模拟时,按照建筑结构荷载规范取体形系数μz=1;C类地貌风压高度变化系数μs=0.65;海拔高度Z=1 890。
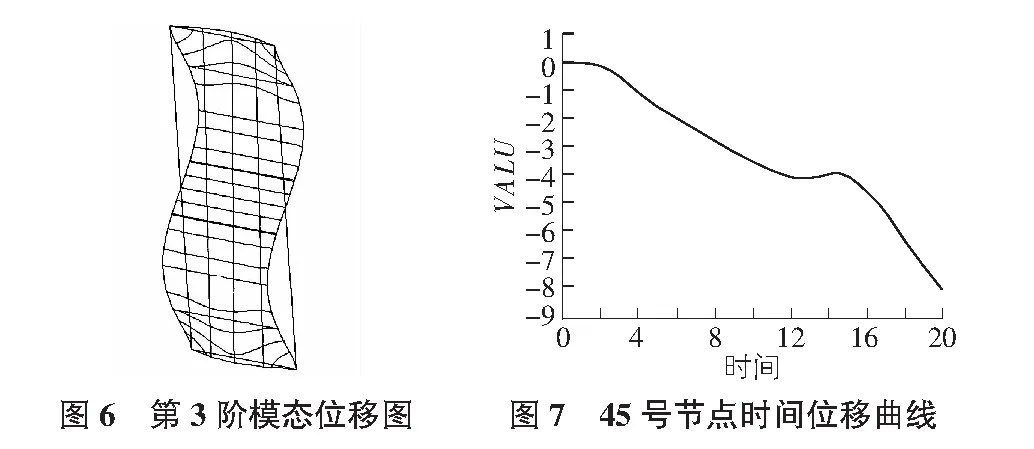
提取第3阶模态振型位移云图,如图6所示。从图6中可以看出位移最大值出现在上下两部分的中间位置,达到了0.067 mm。位移最大点45号节点的时间位移曲线如图7所示。
4 结语
针对工程结构中广泛使用的玻璃幕墙,首先采用Davenport风速谱使用MATLAB编制了计算程序模拟脉动风速时程。随后根据规范转换为脉动风荷载。据此建立了时程分析流程,并采用分块Lanczos方法进行模态分析,同时计算了玻璃幕墙的瞬态响应。分析表明结构前3阶振型以弯曲振动和扭转振动为主,在结构设计过程中要注意提高结构的抗剪刚度和抗扭转刚度。
[1] 王莺歌,李正农.索桁式玻璃幕墙风荷载时程模拟及风振响应[J].昆明理工大学学报(自然科学版),2011,36(2):26-31.
[2] 尹晓江.玻璃幕墙结构动力学分析与数值模拟[D].济南:山东建筑大学,2006.
[3] 刘锡良,周 颖.风荷载的几种模拟方法[J].工业建筑,2005,35(5):81-84.
[4] Davenport A G.The relationship of wind structure to wind loading[A].Proc.of the symposium on wind effect on building and structures,London[C].1965:54-102.
[5] 周 云.结构风振控制的设计方法与应用[M].北京:科学出版社,2009:43-44.
[6] Chen L,Letchford C W.A deterministic-stochastic hybrid model of downbursts and its impact on a cantilevered structure[J].Engineering structures,2004,26(5):619-629.
[7] Chen Lizhong,Chris W.Letchford.Simulation of multivariate stationary Gsussian stochastic processes:hybrid spectral representation and POD approach[J].Journal of engineering mechanics,2005,131(8):801-808.
[8] JGJ 102—2003,玻璃幕墙工程技术规范[S].
[9] GB 50009—2012,建筑结构荷载规范[S].
Dynamic response analysis of frame aluminum alloy glass screen wall★
Fu Shuyan Huang Haiyan Yang Lifan
(CollegeofWaterConservancy,YunnanAgriculturalUniversity,Kunming650201,China)
The simulation program with MATLAB is used to simulate the fluctuating wind based on the Davenport wind velocity spectrum. The fluctuating wind load can be gotten according to the standard. The time history analysis process is established. And then the modal analysis and the time history analysis are done. The results can provide design reference for practical engineering.
glass screen wall, wind load, modal analysis, time history analysis
1009-6825(2017)05-0029-02
2016-12-04★:云南省教育厅基金(2016ZZX109)
傅蜀燕(1976- ),女,博士,讲师; 黄海燕(1975- ),男,博士,教授; 杨立凡(1993- ),男,在读硕士
TU311
A

