基于突变理论的岩质边坡失稳预警模型

郭朝旭

(1．福建省建筑科学研究院 福建省绿色建筑重点实验室 福建福州 350025;2.福州大学 福建福州 350108)

基于突变理论的岩质边坡失稳预警模型

郭朝旭1,2

(1．福建省建筑科学研究院 福建省绿色建筑重点实验室 福建福州 350025;2.福州大学 福建福州 350108)

以某岩质边坡为例，利用FLAC有限差分软件分析不同折减系数下位移变形特征，然后利用尖点突变理论分析岩质边坡的临界折减系数，从而建立岩质边坡失稳判断新的预警模型。

岩质边坡；预警模型；突变理论

0 引言

边坡的稳定性评判是一个艰难而复杂的过程，因为边坡的稳定性是边坡地质环境和人为因素共同作用的结果，且这些因素很大程度上又具有可变性、不确定性和随机性等特点。当前，关于边坡的稳定性评价方法大致可分为以下两种：确定性分析方法和不确定性分析法[1～6]。由于边坡稳定性的影响因素较多，且各个因素之间的关系又具有不确定性，因此在边坡稳定性评价过程中就带有一定的模糊性和不确定性。边坡破坏必然会伴随着一些比较直观或者潜在的变化，如裂缝及位移的产生。这些变化与边坡的稳定性之间存在一定的内在联系。如果能够准确地掌握这些变形与边坡稳定性之间的关系，便能迅速地对边坡的稳定状态加以判断，从而减少由此带来的一些不必要的损失。

本文以FLAC有限差分软件为基础，对比分析不同强度折减系数条件下边坡的最大位移变化趋势，然后利用突变理论对该位移变化情况进行对比分析，得到位移突变条件下的强度折减系数，从而判断该边坡的稳定状态。

1 位移预警模型

边坡发生变形是一个连续的过程，但边坡的破坏往往是在一瞬间完成的，在这个过程中，边坡的位移会有突变现象产生，以点的位移突变作为评判边坡稳定性的依据具有非常明显的物理意义，而且直观可靠，为了减少主观因素的影响，本文选择边坡的最大竖直位移作为分析研究的基础，根据突变理论，以尖点突变模型为原型建立评判标准。

(1)突变理论简介

1972年法国数学家Thom创立了突变理论，该理论建立在拓扑动力学、微积分、奇点理论以及结构稳定性等数学理论之上，用来描述自然界中大量存在的不连续的突然变化现象，其特点是，根据一个系统的势函数将它的临界点进行分类，研究各类临界点附近非连续变化处的特征，从而归纳出突变模型[1～2]。

(2)评判标准的建立

本文以Flac3D软件为基础对边坡的位移变形进行计算分析，在岩土体材料强度不同折减系数下分别进行计算，以往往往利用数值计算的收敛性、特征部位位移的突变性及塑性区的贯通性作为边坡失稳的判断依据[5]。然而，以上各种方法未能建立统一标准，根据突变理论，釆用尖点突变模型，对Flac3D下的边坡强度折减法计算过程中得到的边坡最大位移进行分析，构建边坡位移失稳破坏的突变模型，从而构建边坡位移发生突变时的强度折减系数即稳定性系数，反映边坡在各工况条件下的状态。建立边坡各强度折减工况下最大位移与折减系数的突变模型如式(1)所示：

δ=F(k)

(1)

折减系数的分级取值，可得到相应级数下的最大竖直位移，对每级的折减系数和最大竖直位移进行多项式拟合，就构建出下式的表达式，经分析，取5次式时，可满足精度要求如式(2)所示：

δ=a0+a1k+a2k2+a3k3+a4k4+a5k5

(2)

对上式求导得势函数如式(3)所示：

V=a1+2a2k+3a3k2+4a4k3+5a5k4

(3)

令q=a4/5a5,k=p-q，并带入上式可以得到如式(4)～(8)所示：

V=b0+b1p+b2p2+b4p4

(4)

b0=5a5q4-4a4q3+3a3q2-2a2q+a1

(5)

b1=8a4q2-6a3q+2a2

(6)

b2=30a5q2-12a4q+3a3

(7)

b4=5a5

(8)

(9)

式(9)为以u,v为控制变量的正则尖点突变模型和对偶尖点突变模型的标准势函数。对式(9)求导，令导数为0，如式(10)所示：

r3+ur+v=0(正则),-r3+ur+v=0(对偶)

(10)

把上式决定的临界点集称为平衡曲面，其在(r,u,v)空间中的图形，上下叶稳定，中叶不稳定，无论u,v沿什么途径变化，相点(r,u,v)只在上叶或者下叶平衡的变化，当相点(r,u,v)到达上下叶边缘时发生突跳跃过中叶，因此，在平衡曲面竖直切线的点构成状态的突变点集，其方程为如式(11)所示：

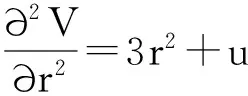
(11)

联立上述两式，消去r，得到所以对于边坡稳定有如下判据，Δ>0稳定，Δ<0不稳定，即判断上述二次方程的实数根是否存在，通过对比可以得到式(12)～(13)：

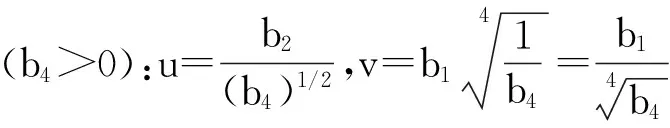
(12)

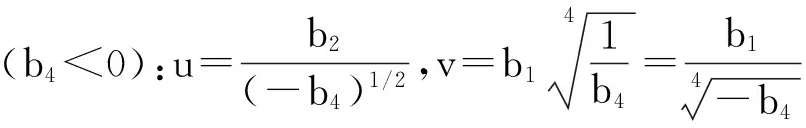
(13)

2 工程边坡概况

以马尾沿山公路边坡B段中BK0+580-BK0+740段，边坡最大高度约50m，属高陡岩质边坡。坡顶为马尾区委党校，边坡北侧为马尾中学。该边坡表层覆盖层较薄，坡面基本为中微风化岩，坡面节理裂隙发育，边坡整体稳定主要受结构面控制，如图1所示。2015年8月开始坡面修正开挖施工，2015年11月完成开挖。支护方式：从上向下四级坡体，第一、二级锚杆长度为15m，用32mm的精轧螺纹管，锚固力200KN；第三、四级放坡，锚杆支护长度为12m，用两根20mm的三级钢钢筋，锚杆与水平夹角为20°，锚固力100kN。

图1 破碎岩体坡面

2.1 地层岩性

地貌单元主要为剥蚀残山地貌单元，场地自上而下土层主要有：

(1)粉质粘土：灰黄色，硬塑，湿。以粘粒、粉粒为主。

(2)凝灰熔岩坡积粘性土：局部表现为残积粘性土，为凝灰熔岩(J3n)风化残积而成。褐黄、灰黄色、可塑、湿等特征，为凝灰熔岩(J3n)坡积而成。可见原岩残余结构，具有遇水易软化特征，主要由粘、粉粒组成，坡积成因。

(3)全风化凝灰熔岩(J3n)：浅黄色、灰白色，凝灰结构，散体状构造，岩体裂隙极发育，岩芯呈土状，手捏易散，遇水易软化、崩解，岩石坚硬程度属极软岩，岩体完整程度属极破碎。

(4)砂土状强风化凝灰熔岩(J3n)：浅黄色、灰白色，凝灰结构，散体状构造，岩体裂隙极发育，岩芯呈砂土状，手捏易散，遇水易软化、崩解，岩体完整程度属破碎，岩体基本质量等级为Ⅴ级。

(5)碎块状强风化凝灰熔岩(J3n)：灰黄色，凝灰结构，碎裂状构造，岩体隙裂极发育，岩芯呈碎块状，岩石坚硬程度属较软岩，岩体完整程度属破碎，岩体基本质量等级为Ⅴ级。

(6)中～微风化凝灰熔岩(J3n)：局部表现为变粒岩和浅粒岩。浅灰色、褐紫色，凝灰质结构，块状构造，岩石裂隙较发育，岩石坚硬程度属较硬岩，岩体完整程度属较完整-较破碎，岩体基本质量等级为Ⅲ-Ⅳ级。

2.2 水文地质条件

地下水类型主要包括：

(1)上层滞水：主要赋存于杂填土中，地下水量一般，补给主要为大气降水及地表径流入渗，排泄方式主要向地势低处侧向排泄，部分为蒸发和下渗。

(2)基岩孔隙-裂隙水：主要为赋存于风化岩中的裂隙水，由于风化程度不同，风化裂隙率和连通性差异较大，其透水性不均匀，总体透水性较弱，富水性也较弱。

3 位移预测结果与坡体稳定状态

为了对该模型进行验证和分析，采用FLAC快速有限差分软件对马尾区沿山通道二期边坡工程19-19’剖面进行分析，观察在不同折减系数条件下岩土体的最大位移情况，利用本文提出的基于尖点突变模型的边坡失稳机制判别模型对该边坡进行安全稳定性评价。计算参数如表1所示，模型及结果详见图2～图4。

表1 计算参数

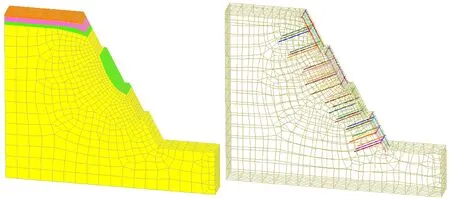
图2 Flac模型简图(左侧为岩土体模型，右侧为支护模型)

图3 不同强度折减系数条件下x方向位移分布

图4 不同强度折减系数条件下剪应变增量分布

图5为竖直方向最大位移和折减系数图，根据上文讨论，由式(对折减系数和最大位移进行多项式进行拟合，由图5可知，突变在1.4左右，所以，列出各级拟合的计算过程，详细说明尖点突变模型的计算方法。

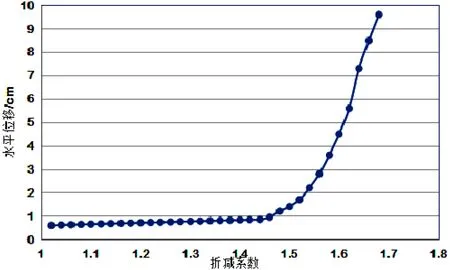
图5 最大位移和折减系数图

拟合级数和△的值如表2、图6所示。由图6可见，随着拟合级数的增加，逐渐减小，据前面分析可知时当△>0时边坡为稳定，当△≤0时，边坡就处于不稳定状态了，因此通过上图的分析可以看出，在折减系数为1.42时，边坡处于稳定状态，而1.44时边坡就失稳了，这时虽然位移突变模型有解，但得到的无意义的物理值，因此此时边坡的稳定系数可确定为1.42，而此折减系数条件下的位移最大发生在坡面中部位置，水平位移为8.45mm(此边坡变形预警值为边坡支护完成后的位移数值)，因此可以通过检测该部位的位移，结合位移监控预测模型，可以对边坡进行风险评估和预测。

表2 拟合级数、对应折减系数与△的值 个

图6 拟合级数和△的值

因此，可以通过降低结构面的参数，从而得到坡体的位移；而该位移与边坡稳定性的关系是通过尖点突变理论建立的联系，这样在今后可以对位移进行监测或者结构面控制的岩质边坡位移进行神经网络训练分析，从而得到不同折减系数下边坡的最大位移，根据尖点突变模型获取边坡的稳定性，从而实现可以评判由结构面控制的岩质边坡的稳定性，避免现有安全系数评判的不合理和不确定性。判别流程如图7所示。

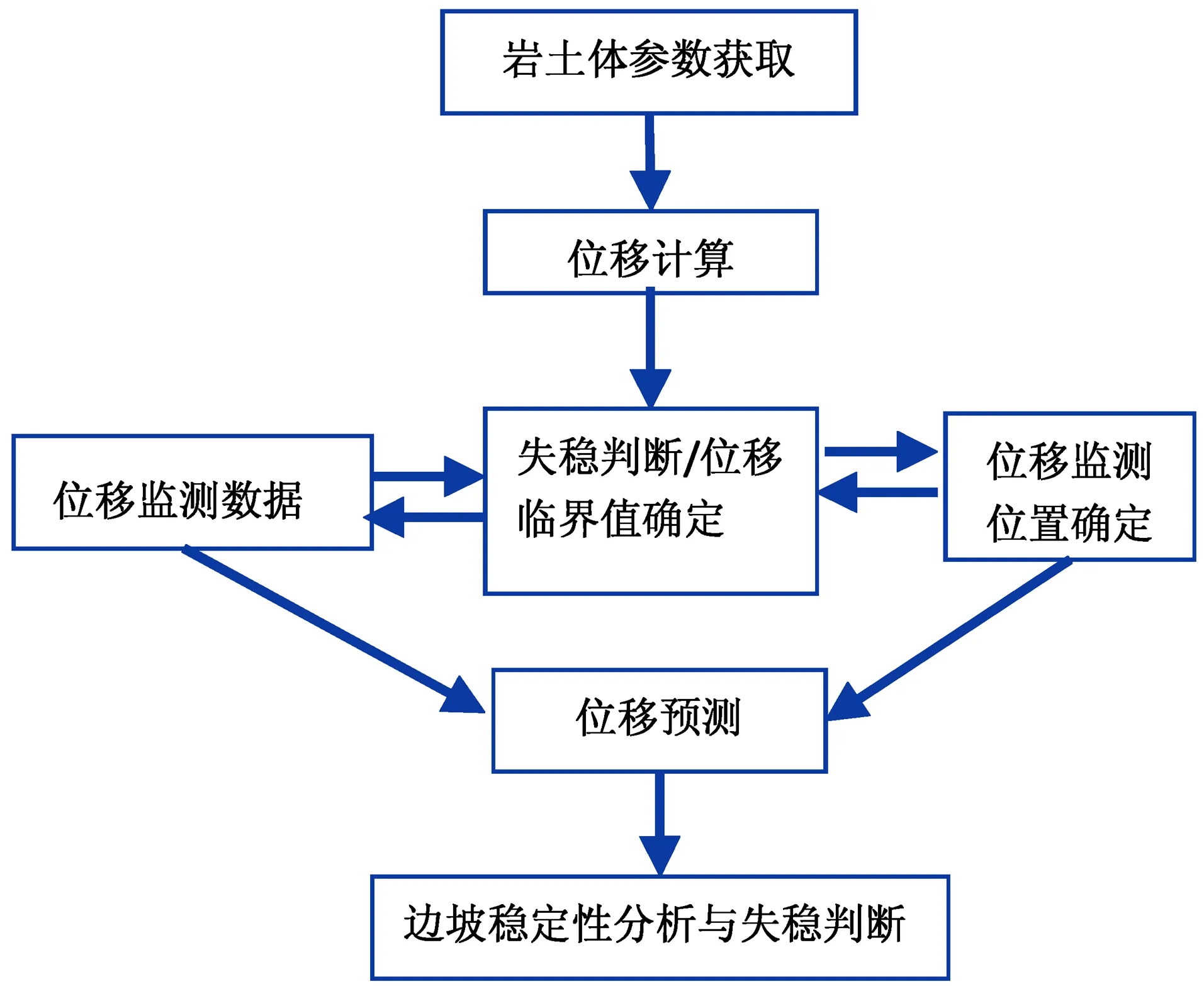
图7 边坡位移预警模型分析流程

4 结语

通过对岩质边坡安全监控模型的研究，总结并建立了岩质边坡监控预测模型，并根据岩质边坡失稳破坏机理，建立了基于尖点突变理论的边坡稳定性评价模型，可以为岩质边坡监测——预警——评估体系提供另一种思路和解决方法，具体如下：

利用快速拉格朗日有限差分软件FLAC对边坡进行位移计算，这里通过强度折减法折减结构面或坡体材料参数获取不同折减系数条件下边坡的最大位移以及所处的位置；建立不同条件系数与最大位移的关系，利用尖点突变模型分析边坡的失稳临界状态，即失稳临界位移值，从而建立边坡临界最大位移，位移所处的位置与位移监测量的关系；同时可以利用监控量预测模型(神经网络与灰色模型)对边坡的稳定性进行预测分析。

[1] 黄昌乾,丁恩保.边坡工程常用稳定性分析方法[J].水电站设计,1999,15(1):53-58.

[2] 李世海,刘天苹,刘晓宇.论滑坡稳定性分析方法[J].岩石力学与工程学报,2009,28(2).

[3] 魏丽敏,何群,林镇洪.考虑地下水影响的滑坡稳定性分析[J].岩土力学,2004,25(3):422-426.

[4] 莫伟伟,徐平,丁秀丽.库水位涨落对滑坡稳定性影响研究进展[J].地下空间与工程学报,2006,2(6):997-1002.

[5] 程杰.基于变形数据的边坡稳定性评判方法研究[D].重庆：重庆交通大学,2014.

[6] Carrara A, Cardinali M, Detti R, et al. GIS techniques and statistical models in evaluating landslide hazard[J].Earth surface processes and landforms,1991,16(5):427-445.

A Instability Prediction Model for Rocky Slope Based on Catastrophe Theory

GUOChaoxu1,2

(1.Fujian Academy of Building Research, Fujian Key Laboratory of Green Building Technology,Fuzhou 350025; 2.Fuzhou University, Fuzhou 350108)

Taking a rock slope as an example, its stability had been predicted by using Flac 3D software under different on reduction factors. Then the critical safety coefficient was analyzed by catastrophe theory. This method is different from the common strength reduction method, and verified to be suitable for rock slope.

Rock slope; Forewarning model; Catastrophe theory

郭朝旭(1987.8- )，男，工程师。

E-mail:guochaoxu177@163.com

2016-12-19

TU472

A

1004-6135(2017)03-0068-04