基于SMO-SVM的丝杠表面磨削质量预测

王蓝博，李郝林，迟玉伦

(上海理工大学 机械工程学院，上海 200093)

基于SMO-SVM的丝杠表面磨削质量预测

王蓝博，李郝林，迟玉伦

(上海理工大学 机械工程学院，上海 200093)

针对滚珠丝杠磨削过程在线监测困难的问题，使用支持向量机建立智能模型。模型本身针对颤振分类和粗糙度预测的不同问题，选用基于串行优化算法的支持向量分类机和支持向量回归机，并使用交叉验证法对模型参数进行优化。基于滚珠丝杠表面波纹度理论和粗糙度理论，对磨削过程中的振动信号进行特征提取，结合加工参数作为模型输入，先进行颤振的判别，在判断未颤振的情况下对表面质量进行预测。实验结果表明，该模型可以对颤振分类及粗糙度预测进行较好的在线监测。

滚珠丝杠；支持向量机；串行优化算法；振动信号

滚珠丝杠被广泛应用于各种工业设备和精密仪器，其加工精度直接影响设备和仪器的传动精度。磨削是加工高精度滚珠丝杠的关键环节。在磨削加工中，如何更好的监测丝杠磨削过程并预测工件表面质量是整个工艺中的重点和难点。监测问题作为表面质量控制的手段之一，有着重要的研究意义。

丝杠的表面质量包括波纹度和粗糙度。为了解决丝杠磨削加工中各种因素高度耦合的问题，选择使用智能模型对丝杠磨削的加工进行预测，以达到在线评估丝杠质量的目的。对于常见的智能模型，一般的统计过程法或实验回归法对训练样本本身分类较准确，对未知样本则误差较大[1-2]；隐马尔可夫模型法分类准确率较高，但模型较为复杂且鲁棒性差[3]；贝叶斯网络模型易于构造和使用，但分类精度相对较低[4]；人工神经网络在处理状态监测的非线性问题中效果较好，但由于其算法本身研究的是样本数趋于无穷大时的渐进理论，在处理样本数有限的实际问题中，会有分类精度差、易陷于局部最优等诸多问题[5]。支持向量机[6]是在传统神经网络算法的原理上发来而来的机器学习方法，它在处理小样本非线性问题上有着明显的优越性。在丝杠表面质量监测中，支持向量机以结构风险最小化原理为基础，兼顾训练误差最小化和置信范围最小化的原理的特点使得它可以在更少的样本中提取出有效模型。而它应用凸二次规划的特点则保证了极值解的全局最优性。此外还有着模型参数简单、结构清晰的优点。因此选择支持向量机作为丝杠磨削表面质量监测的智能模型。本文将使用支持向量机对波纹度和粗糙度预测问题进行研究。

1 理论基础

1.1 丝杠表面波纹度理论

颤振的主要来源是自激振动。由磨削自激振动的动力学模型[7]可知，砂轮转速、工件转速以及磨削深度和颤振的发生最为相关，因而和工件波纹度也最为相关。此外，振动是颤振的最为直观的反映。由图1所示，在相同的传感器位置和振动方向监测相同参数的工件，在控制其他工艺参数不变的情况下，略微增大磨削深度使得工件颤振。不难看出，颤振前后的振动信号在时域和频域的幅值上都有着明显的变化。因此提取振动信号的峭度、砂轮转速、工件转速及磨削深度作为模型输入。

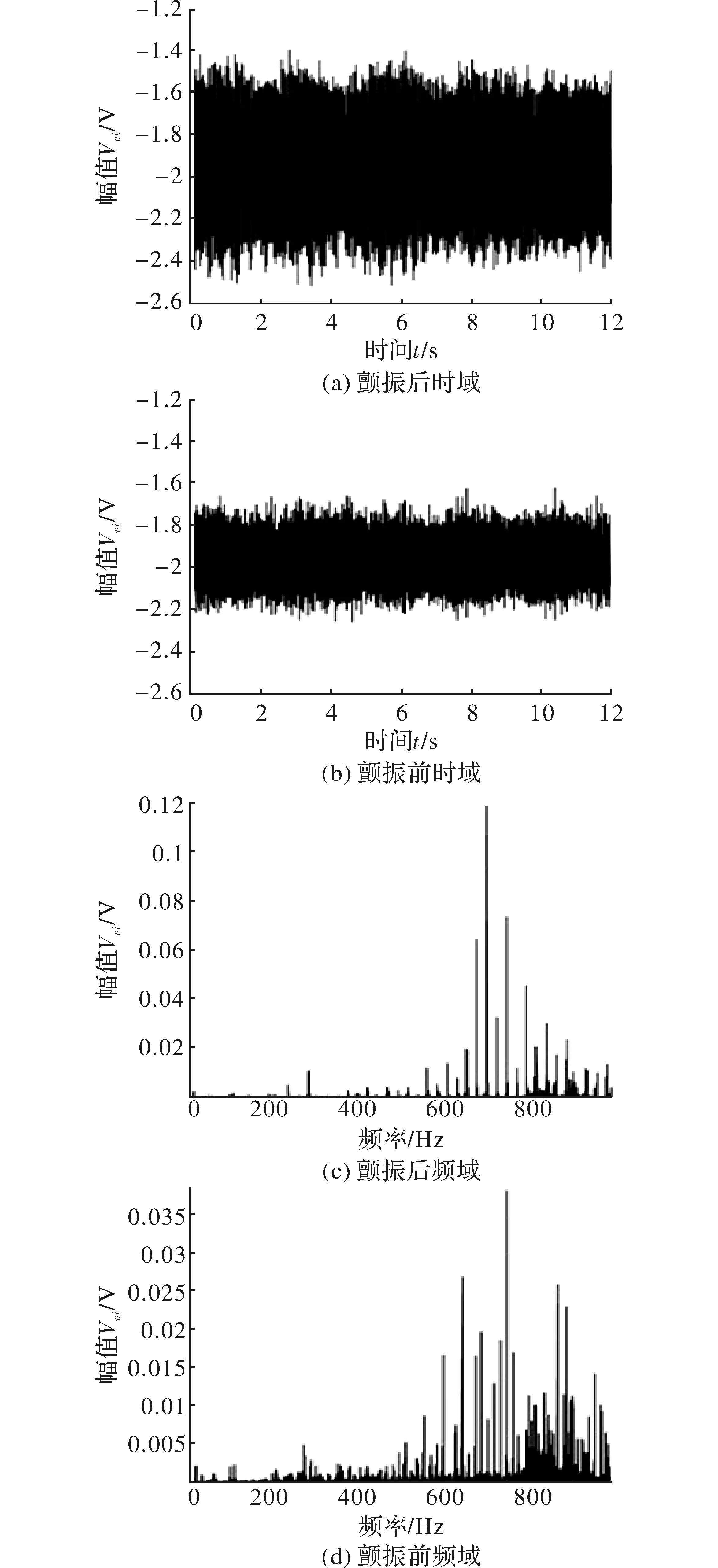
图1 颤振与非颤振的振动信号对比图

1.2 丝杠表面粗糙度理论

Shaw在1996年定义了等效磨屑厚度，并发现这一参数可以很好地表征粗糙度、磨削能量以及磨削钝化，且可以应用于任何一种磨削方式中。在此基础上，引入总磨削能量，得到表面粗糙度的表达式

(1)

其中，Rt代表在轮廓评价长度内峰和谷的最大距离；hcu为等效磨屑厚度；ae为磨削深度；vg为工件转速；vw为砂轮转速；ρ表示磨粒形状系数；Ce为砂轮单位面积上切削刃数目，砂轮等效直径为砂轮等效直径成反比，和磨粒形状参数成反比。此外,Tawakoli于2008年的研究表明[8]，在砂轮转速不变的情况下，磨削能量和振动信号的峭度值有着成正比的关系。因此可得

(2)

其中，ec为磨削必能；bw为砂轮宽度；Vvi为振动信号的均方根值。可见，在磨削深度和工件转速不变的情况下，振动信号的峭度值和工件的表面粗糙度成反比。因此，振动信号的峭度值可作为工件表面粗糙度的一个反馈信息。

此外为了进一步讨论其他影响因素，引入修整工艺参数。本文中的修整为切入式修整，在整个过程中没有纵向的进给，不涉及重叠率等参数。在砂轮转速固定的情况下，修整的横向进给速度直接决定磨粒形状参数，而磨粒密度则保持不变。因此，修整进给速度也是决定表面粗糙度的重要因素。磨削深度则是影响应变和亚表面状态最主要的工艺因素。因此，粗糙度预测模型应该将磨削深度纳入考虑范围。

因此，使用振动信号的峭度值、工件速度、砂轮转速、修整进给速度以及磨削深度作为丝杠表面粗糙度评价的输入向量。

2 总体结构与流程

2.1 硬件部分

丝杠的加工磨削和砂轮修整统一在一个坐标系中，通过数控系统循环进行工作。试验平台基于SK7432×4000精密丝杠磨床；使用粒度为60目,直径为500 mm的白刚玉异型丝杠砂轮磨削材料为GCR15钢的淬硬丝杠工件(40.5×5R-P3/500×400)；砂轮通过异型非转动的修整器进行切入型修整；通过对修整进给速度、工件转速、砂轮转速以及磨削深度进行调整，从而得到泛化性较强的试验样本。在此基础上，设计L9(34)正交试验。

信号采集系统主要包括传感器、数据采集卡、计算机以及辅助器件(包括直流电源、信号传输电缆、前置放大器等)。

2.2 软件部分

由于丝杠的波纹变化的是由颤振产生的，且颤振与振动信号息息相关，因此使用振动信号配合支持向量分类机对颤振进行判断；由于丝杠的粗糙度值和振动信号的均方根直接相关，所以使用支持向量回归机对粗糙度值得大小进行回归拟合。此外，颤振引起的波纹度变化会在很大程度上影响粗糙度的评估，且颤振后的丝杠已可被判定为报废，再进行粗糙度评价已没有意义。因此应优先考虑颤振的判断，再进行粗糙度的拟合。

3 实验数据处理

3.1 滚珠丝杠表面磨削质量的测量

丝杠表面质量的测量通过多功能轮廓仪实现。由图2可知，波纹度的评估使用颤振与否来衡量，而粗糙度的评估则通过具体数值来表征。测量后，将采样线段拉直，可见颤振工件的轮廓呈明显的叶瓣形分布，且Ra等评价指标都很大，如图3所示，而非颤振则没有明显的分布规律，且评价指标相对较小，如图4所示。在此基础上，设定图3和图4中相同采样距离的表面轮廓线和y=0的交点数目为颤振系数，当此数目>10时设为非颤振，反之为颤振。因此，可以得到丝杠颤振与否的判断。

粗糙度方面，选择使用轮廓评价长度内的最大峰谷间高度Rt作为指标。

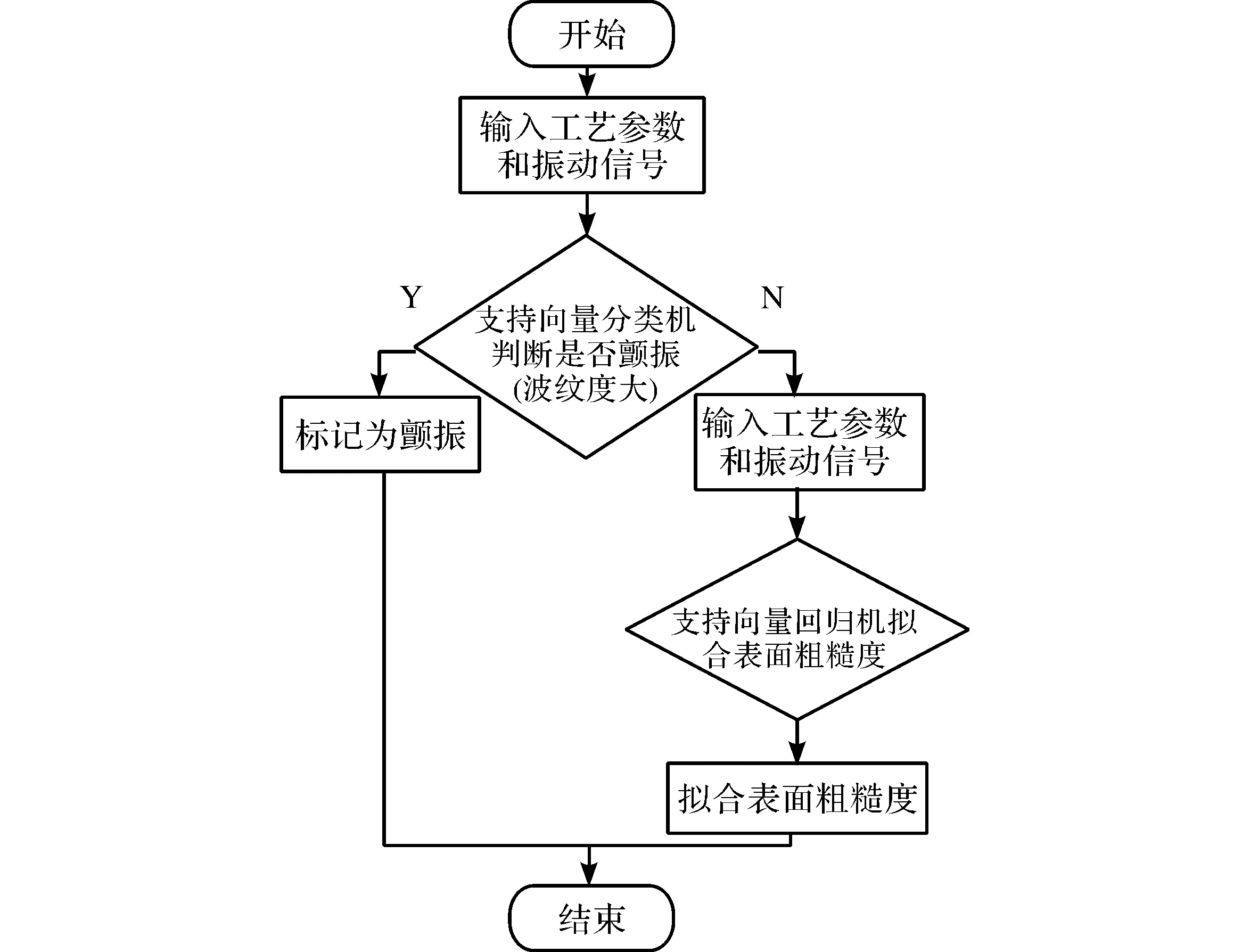
图2 滚珠丝杠表面质量智能监测流程图

3.2 振动信号的处理和提取

支持向量机的输入样本由磨削工艺参数和传感信号特征参数构成。其中，传感信号则需要一定的处理，可以分为以下两个步骤：分段处理和特征提取。

首先使用幅值筛选法将整个丝杠磨削的信号提取出来。之后根据测量丝杠表面质量时固定的轴向位置，对应得到信号的位置，再上下各取6 s的信号，从而得到长度为12 s的信号段，且能对应粗糙度值和颤振状态。

在此基础上对振动信号进行表征。根据式(2)的结论，选择使用峭度作为振动信号的特征参数，其数学形式为

(3)其中，Vvi为振动信号的峭度；VIraw(λ)为原始振动信号；N为时间段内的采样点数，取值为24 000。至此，已将采集的声发射信号和振动信号转化为参数样本，结合工艺参数即可构成支持向量机的输入样本集。得到了可以用于支持向量机训练和验证的样本库。为使数据可以直接被支持向量机使用，在训练模型之前应用前处理方法：归一化处理和主成分分析处理。

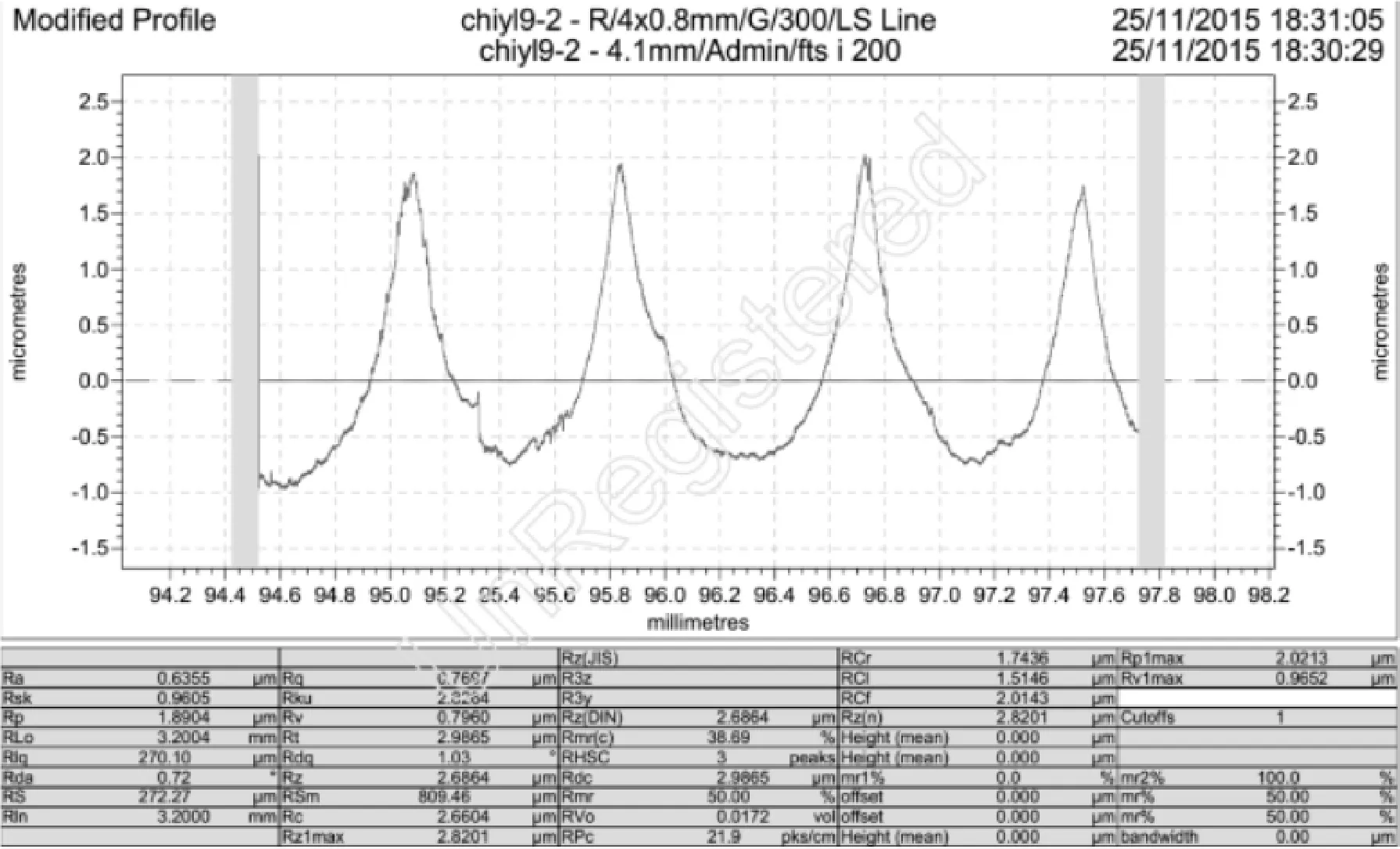
图3 颤振工件的波纹度测量结果

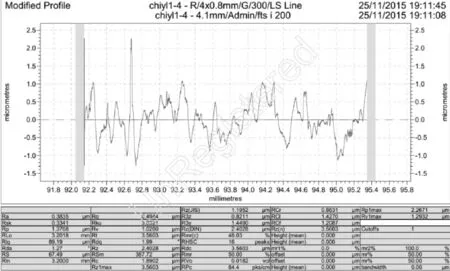
图4 非颤振工件的波纹度测量结果

4 支持向量机模型的建立和验证

4.1 支持向量机模型

支持向量机是建立在VC维理论和结构风险最小化理论基础上，专门针对小样本问题的数据挖掘方法。支持向量机的回归和分类相比，增加了一个控制回归精确度的误差系数ε，用来定义目标值和预测值得差值满足要求的程度。此外，定义软边界损失函数，使得在ε带以外的预测值被惩罚，以增加系统鲁棒性。在此基础上，可把回归问题等效为分类问题。

4.2 凸二次规划转化

分类和回归问题引入松弛变量和惩罚系数可以转化为二次规划问题

(4)

其中，使用函数Ø将输入向量映射至高维的特征空间以满足非线性分类的需要。C表示错误分类或预测误差的惩罚系数，xi代表用于提高模型容错率的松弛变量。

引入核函数的定义

K(xi,xj)=φ(xi)Tφ(xj)

(5)

本实验选择使用结构简单、性能优越的径向基函数作为模型的核函数，避免因升维导致的维数灾难[9]。在此基础上，引入拉格朗日函数对模型进行处理，得到了模型的凸二次对偶问题

(6)

至此，可将支持向量机的求解等效为一个凸二次规划问题。凸二次规划问题的转化模型保证了满足KKT条件[10]的局部最优解一定是全局最优，大幅提高了支持向量机的稳定性和可靠性。

4.3 串行优化算法求解凸二次规划

由上述讨论可得，支持向量机的训练即是求解凸二次规划问题。为减少运算量和内存，实验选择使用串行优化算法优化此运算。即每次只选取两个拉格朗日乘子进行优化，再更新模型。

简化KKT条件并得到SMO算法的停机准则

(7)

当Pi为零时，表示所有样本满足KKT条件，算法停止，从而得到解析解。

4.4 交叉验证法优化模型参数

在选择支持向量机时，针对颤振的在线判断问题使用了C-SVC；针对丝杠表面粗糙度的监测则使用了ε-SVR。应用过程中发现，支持向量机的全局优化和神经网络不同，不能自适应的优化模型参数，参数的选择对分类的精度和效率有着极大影响。针对这个问题，使用交叉验证法对模型参数进行优化[11-13]。

本实验采用的交叉验证使用以下步骤：首先将训练样本n等分，用每一份样本作为验证集，其他n-1样本作为训练集。所以，会得到n个模型，使用这n个模型的分类准确率或回归均方差作为评价指标，以得到最佳的模型参数。

交叉验证法只是一种载体，需要搭配一个确切的最优化方法才能实现。实验验证表明，针对本文使用的核函数和损失函数，支持向量分类的两个模型参数C和γ应使用网络搜索法最为合适；而对于支持向量机回归的3个模型参数C、γ和ε应选用遗传算法效果最佳。

4.5 结果验证和对比

按照图2的总体流程，先对颤振进行分类。为了提高所训练模型的泛化能力，不失一般性的从样本库中随机选取33组样本作为训练集，33组为测试集。训练时，设置交叉验证系数为5(样本分为5份)，使用双参数网络搜索法，设置C和γ范围为[-8，8]，步长均为0.5。得到C=0.353 55，γ=0.176 78，训练时间为2.267 4 s，训练集分类精度为100%，测试集分类精度为100%。

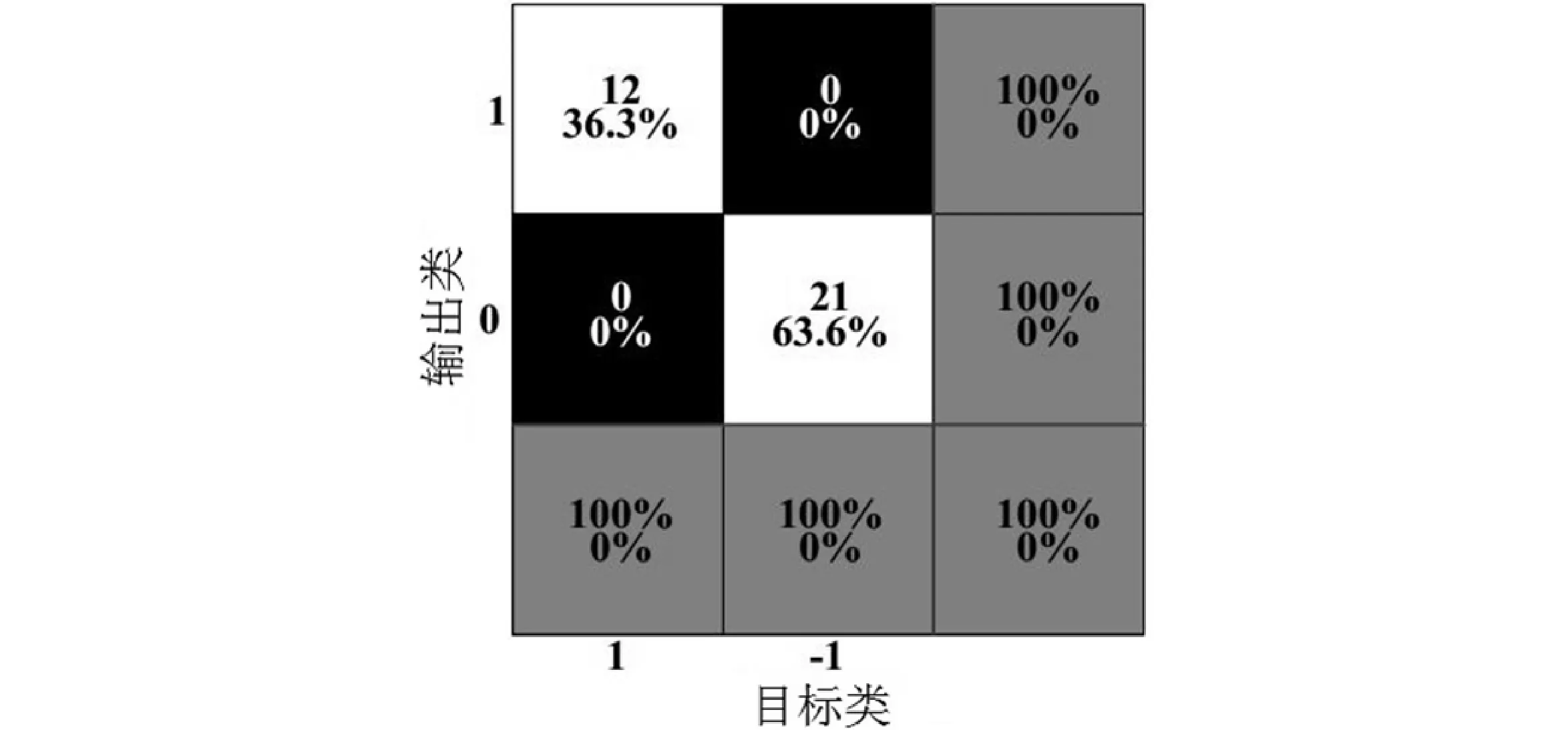
图5 训练集颤振分类的混淆矩阵

图6 测试集颤振分类的混淆矩阵

接着对颤振进行分类。筛选出非颤振的48组样本，从样本库中随机选取24组样本作为训练集，24组作为测试集。训练时，设置交叉验证系数为5(样本分为5份)，使用3参数遗传算法，设置进化代数为100，初始种群数量为20，C和γ范围为 ，步长为0.5，ε范围为 ，步长为0.5，得到C=1.245 7，γ=7.958 2，ε=0.184 97，训练时间为5.342 2 s，训练集的均方误差为0.284 6，测试集分类的均方误差为0.604 5。

由图5～图8的结果可以看出，本实验所建立的支持向量模型可以对颤振分类以及粗糙度回归的预测进行较好的在线监测。其中，颤振分类模型的预测分类精度达到了100%，有着较好的效果，可以用于滚珠丝杠磨削的工艺指导以防止颤振；表面粗糙度的预测模型也表现良好。

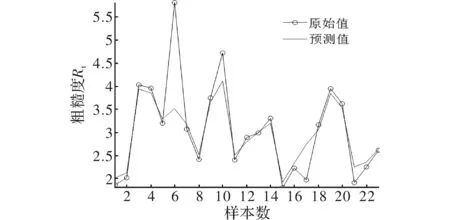
图7 训练集粗糙度拟合的对比图

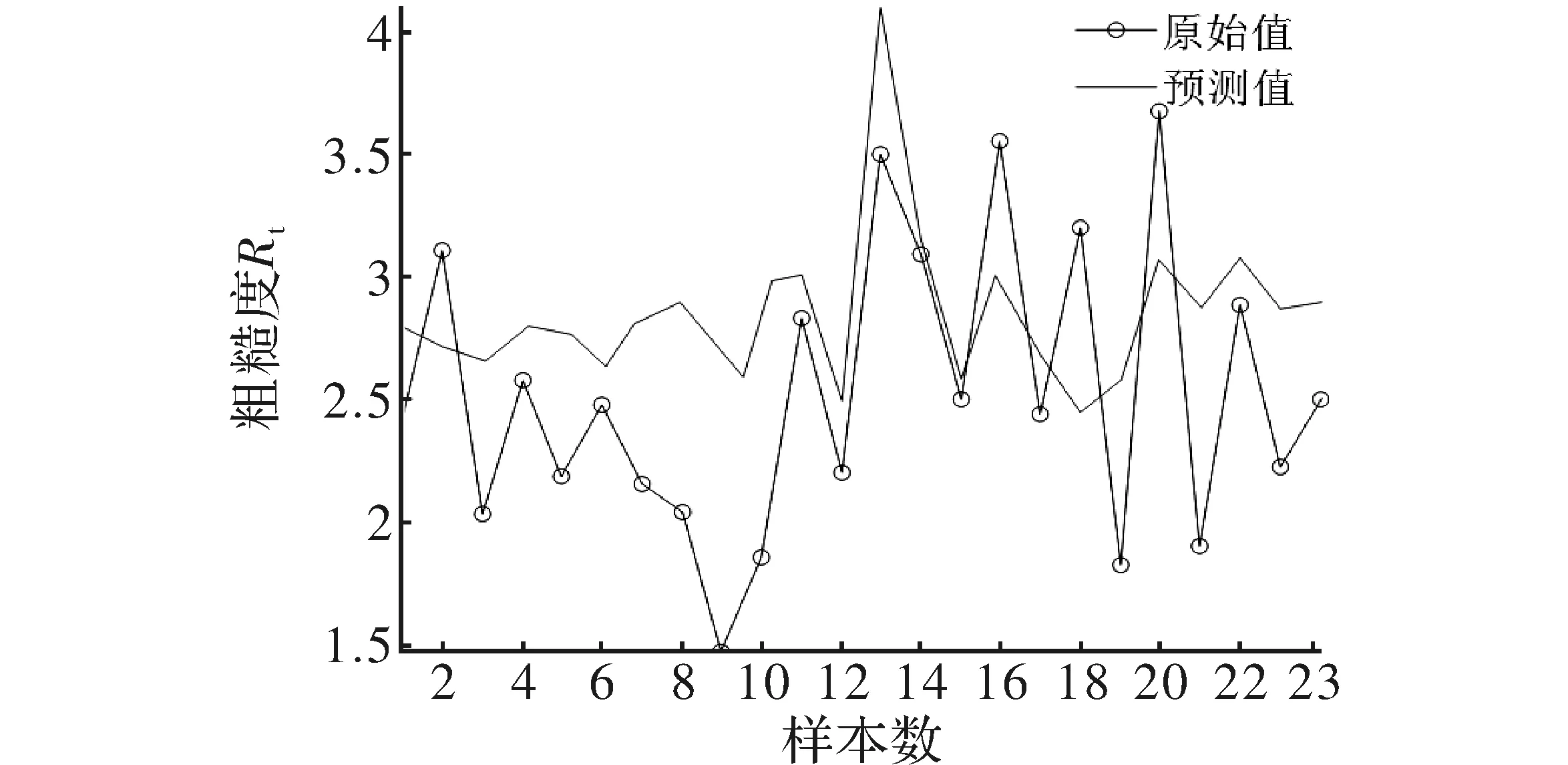
图8 测试集粗糙度拟合的对比图

5 结束语

总体来说，本文较为完整地对丝杠表面质量进行了监测，将表面波纹度和表面粗糙度分别进行了评估，并在颤振监测方面有着较高的监测效率和预测精度。在实验设计方面选用了易于操作的监测方法，搭建时间较短。此外，本文所建立的监测模型可以随着滚珠丝杠的磨削达到在线在位预测丝杠表面质量的效果，比传统的离线停机测量更方便，比单独通过视觉对比的方法更可靠。

[1] Shi D,Axinte D A,Gindy N N.Online machining process

monitoring using wavelet transform and SPC[C].CA,USA:IEEE Instrumentation and Measurement Technology Conference Proceedings,IEEE,2006.

[2] Karpuschewski B,Wehmeier M,Inasaki I.Grinding monitoring system based on power and acoustic emission sensors[J].CIRP Annals-Manufacturing Technology,2000,49(1):235-240.

[3] Liao T W,Hua G,Qu J,et al.Grinding wheel condition monitoring with hidden Markov model-based clustering methods[J].Machining Science and Technology,2006,10(4):511-538.

[4] 林峰,焦慧锋,傅建中.基于贝叶斯网络的平面磨削状态智能监测技术研究[J].中国机械工程,2011,22(11):1269-1273.

[5] Martins C H R,Aguiar P R,Frech A,et al.Tool condition monitoring of single-point dresser using acoustic emission and neural networks models[J]. IEEE Transactions on Instrumentation and Measurement,2014,63(3):667-679.

[6] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-42.

[7] 任庆心,华定安.磨削原理[M].西安:西北工业大学出版社,1988.

[8] Tawakoli T,Rasifard A.Dressing of grinding wheels[M].NY,USA:Springer US,Machining with Abrasives,2011.

[9] Keerthi S S,Lin C J.Asymptotic behaviors of support vector machines with Gaussian kernel[J]. Neural Computation, 2003,15(7):1667-1689.

[10] Keerthi S S,Shevade S K,Bhattacharyya C,et al. Improvements to Platt’s SMO algorithm for SVM classifier design[J].Neural Computation,2001,13(3):637-649.

[11] 于艳美.丝杠磨削加工质量因素分析及实验研究[D].南京:南京理工大学,2011.

[12] 于艳美,李春梅,冯虎田.滚珠丝杠磨削加工中的振动测试与分析[J].机床与液压,2011,39(3):17-21.

[13] 丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1):2-10.

[14] 张永.基于模糊支持向量机的多类分类算法研究 [D].大连:大连理工大学,2008.

[15] 茅嫣蕾,魏贇,贾佳.一种基于KKT条件和壳向量的SVM增量学习算法[J].电子科技,2016,29(2):38-40.

Prediction of Surface Grinding Quality Based on SMO-SVM

WANG Lanbo，LI Haolin，CHI Yulun

(School of Mechanical Engineering，University of Shanghai for Science and Technology，Shanghai 200093,China)

Aiming at the difficulty of on - line monitoring of the grinding process, the support vector machine was used to build the intelligent model. Based on the surface waviness and roughness theory of ball screw, extracted the vibration signal in the grinding process combining with machining parameter are taken as the model input. The support vector machine and support vector regression machine based on serial optimization algorithm are selected for the different problems of flutter classification and roughness prediction. In addition the model parameters are optimized by cross validation. Judge the flutter at first, predicted surface quality in judging the case of non-flutter. The experimental results show that the model can better monitor the flutter classification and roughness prediction.

ball screw;support vector machine;serial optimization algorithm;vibration signal

2016- 10- 20

上海市科学技术委员会科研基金资助项目(15110502300)

王蓝博(1991-)，男，硕士研究生。研究方向：精密加工技术。李郝林(1961-)，男，博士，教授，博士生导师。研究方向：数控技术精密检测与智能控制。

10.16180/j.cnki.issn1007-7820.2017.04.028

TG 333；TP391

A

1007-7820(2017)04-110-05