基于Matlab的S曲线加减速控制算法研究

胡永安，陈彩凤，杨 萌

(上海理工大学 机械工程学院，上海 200093)

基于Matlab的S曲线加减速控制算法研究

胡永安，陈彩凤，杨 萌

(上海理工大学 机械工程学院，上海 200093)

当数控加工型线为折线，路径段与路径段之间存在的夹角使得必须在拐点处进行加减速控制，以保证轨迹精度。目前，数控加工对单个坐标运动的控制方法有多种，其中较有代表性的是基于S型曲线的加减速控制方法，文中在S型加减速控制曲线基础上建立S曲线加减速控制新算法，利用该算法给出路径段几何元素转接矢量夹角数学模型，并在此基础上给出许用速度与夹角的关系式，并得出第i路径段的转接速度Vi的大小不仅受到转接矢量夹角αi的影响，还与第i-1路径段和i+1路径段的转接速度以及第i路径段和第i+1路径段的路径长度有关。利用此算法经Matlab编程仿真得出当相邻两折线段夹角为90°和135°时，通过折线交点时对应各坐标运动速度的变化。

S曲线；转接速度；夹角；Matlab

高速加工要求机床各运动轴均能够在极短的时间内达到高速运行状态，并实现高速准停，研究开发数控加工刀具运动满足高速、高精度要求的、有效柔性加减速控制方法[1]，已成为现代高性能数控系统研究的重点。

当数控机床加工中加工型线为折线时，在指定加工误差(指在加工型线的法线方向上加工型线与刀具实际轨迹的差值的最大值)的条件下，遇到折线交点时机床的运动速度就要发生变化，发生变化后自然就会影响加工效率，为了提高加工效率，就要使运动速度的变化时间变得更短[2]，当然这是在不影响加工精度条件下进行的。现在建立一种速度变化模型来描述运动速度在折线交点处的变化，本文的目标是优化速度。以相邻两折线段夹角为90°和135°时为例，进行讨论通过折线交点时对应各坐标运动速度的变化。

1 S曲线加减速模型和基本公式

目前，数控加工对单个坐标运动的控制方法有多种，其中较有代表性的是基于S型曲线的加减速控制方法。其特点是将加减速过程分为7个阶段[3-7](每一段对应的加加速度为常量)：加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段、减减速段，从而渐变地控制各段的加速度使机床运动速度按S型曲线形式平滑变化，以保证速度光顺，加速度连续，在一定程度上增强机床运行的平稳性[7-8]。S型加减速控制曲线如图1所示。

在基于S型曲线的运动过程中，对于速度和加速度都有一定的限制性要求，速度v不大于机床最大速度vmax，加速度a不大于机床最大加速度amax，加加速度为常量Iconst。

图1中各个阶段的速度、加速度、加加速度随时间的变化规律如下所示。

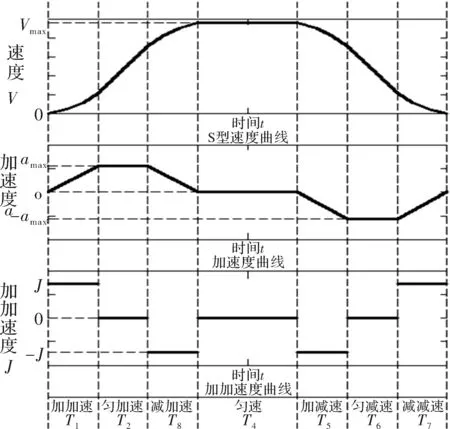
图1 S型加减速控制曲线的速度、加速度、加加速度随时间变化规律

(1)加加速段

(1)

其中，T1=amax/Jconst，这个过程中加速度达到最大amax，加速度和速度均在增加。

(2)匀加速段

(2)

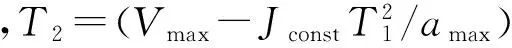
(3)减加速段

(3)

这个过程中加速度在减小，速度在增加，一直增加到Vmax，当t=2T1+T2时，V=Vmax。

(4)匀速段

(4)

这个过程中加速度为0，速度保持Vmax不变，T3的长短由路径长度决定。

(5)加减速段

(5)

这个过程中加速度在增加，速度在减小，这段其实与减加速段是对称的。

(6)匀减速段

(6)

这个过程中加速度保持-amax不变，速度在减小，这段其实与匀加速段是对称的。

(7)减减速段

(7)

这个过程中加速度在减小直到为0，速度也在减小直到为0，当t=4T1+2T2+T3时，V=0。这段其实与加加速段是对称的。

2 S曲线新算法的建立

S型曲线的加减速控制方法中，其特点是将加减速过程分为7个阶段[9-11]：加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段、减减速段，第i路径段的转接速度vi的大小不仅受到转接矢量夹角αi的影响，还与第i-1路径段和i+1路径段的转接速度以及第i路径段和第i+1路径段的路径长度有关，针对折线加工型线，建立以下实时加工优化控制算法。该算法在多段路径加工过程中能有效缩短加工时间。

假设B是拐点，BC为从B点起始指向C点的线段；AB为从A点起始指向B点的线段。Li为初始点为B点所在的路径段长度，(xi,yi)表示B点在平面中的坐标,αi表示AB与BC的偏移角，βi表示BC与X轴正方向的夹角,Vi是B点的速度矢量。

图2 折线图

下面建立B点速度受拐角αi限制的模型。在多路径段加工中，AB与BC为连续路径段,当cosβi、sinβi之中有一个发生符号变化[12-14]，则表明有一轴要发生换向, 在拐角处必须把速度降为0。这种情况就不作讨论了。当已知点A、B和C坐标时，可得

(8)

设AB段的末速度为Vie,BC段的初速度为Vis。假设Vie与Vis大小相等, 其值为Vi, 而Vie与Vis的夹角为αi。根据速度合成关系求得点B的加速度大小为

(9)

设amax为加工过程中最大加速度, 则需满足关系

ai≤amax

其中,T为插补周期。在一个插补周期中,X轴速度的变化为

ΔVX=Vicosβi-Vicosαicosβi+Visinαisinβi

(10)

而Y轴速度的变化为

ΔVY=Visinβi-Visinαicosβi-Vicosαisinβi

(11)

设在一个插补周期内X轴最大允许速度变化为ΔVXmax,Y轴最大允许速度变化为ΔVYmax, 则有

(12)

设定

ΔVXmax=ΔVYmax=amaxT

(13)

其中，amax代表最大加速度值。

由式(8)和式(9)可得速度值限制有如下不等式组

(14)

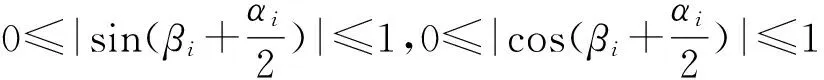
则式(10)可简化为

(15)

式(11)可以当作αi对B点的速度限制，记

(16)

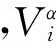
3 S曲线新算法的举例

(17)

其中，amax=0.6 m/s2，T=0.36 ms，αi=90°，0≤βi≤180°。

根据上述条件通过Matlab编程计算得到如图3所示在折点处对应X轴方向运动速度随βi的变化过程。

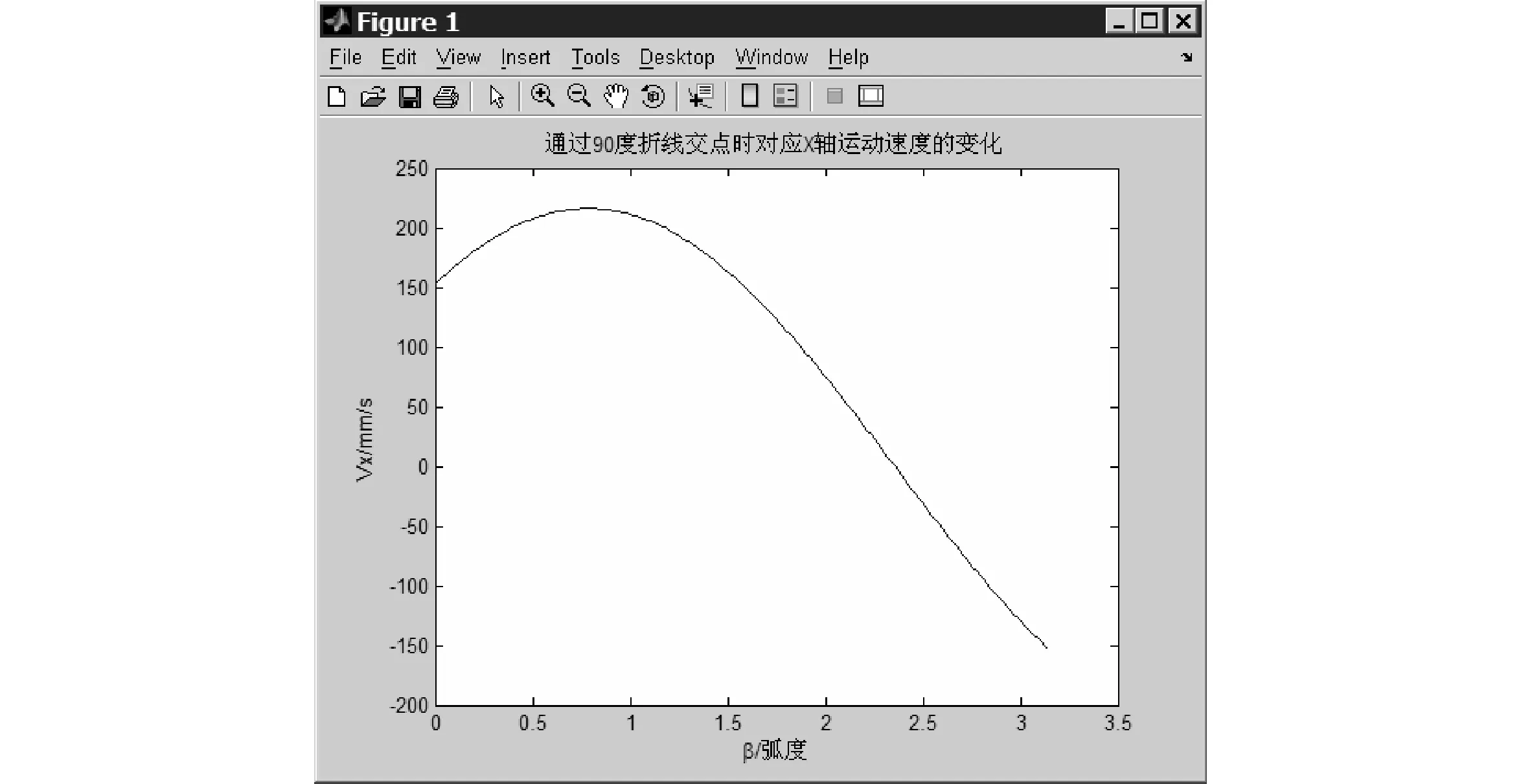
图3 通过αi=90°折点处对应X轴方向运动速度随βi的变化

通过折线交点时对应Y轴方向运动速度的变化函数为

(18)

其中，amax=0.6 m/s2，T=0.36 ms，αi=90°， 0≤βi≤180°。

根据上述条件通过Matlab编程计算得到图4所示在折点处Y轴速度随βi的变化过程。

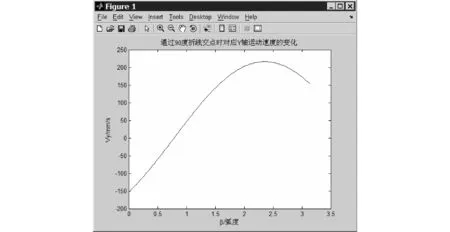
图4 通过αi=90°折点处对应Y轴方向运动速度随βi的变化

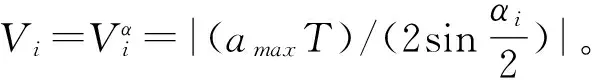
(19)

其中，amax=0.6 m/s2，T=0.36 ms，αi=135°， 0≤βi≤180°。

根据上述条件通过Matlab编程计算得到图5所示在折点处X轴速度随βi的变化过程。

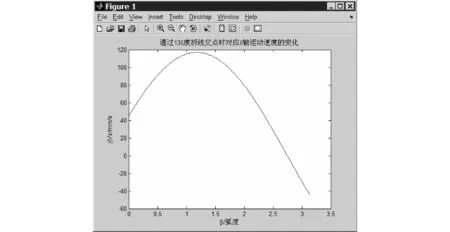
图5 通过αi=135°折点处对应X轴方向运动速度随βi的变化

通过折线交点时对应Y轴方向运动速度的变化函数为

(20)

其中，amax=0.6 m/s2，T=0.36 ms，αi=135°， 0≤βi≤180°。

根据上述条件通过Matlab编程计算得到图6所示在折点处Y轴速度随βi的变化过程。

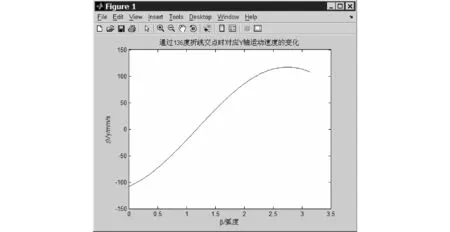
图6 通过αi=135°折点处对应Y轴方向运动速度随βi的变化

4 结束语

本文建立了基于S曲线的拐角过渡模型，该模型满足曲率连续的条件，能显著减小速度波动和机床振动，保证速度平滑转接，实用性强。基于该模型，提出了一种实时加工优化控制算法。该算法在满足加工精度和机床动力学的限制下，能够获得最优转接速度，并举例说明，利用Matlab进行仿真，得出各个方向速度虽角度的变化过程。本算法仅考虑了运动速度与折线夹角的关系，没有考虑机床本身的加工误差，所以需要进一步的探索研究。

[1] 许良元.数控加工中加减速控制曲线的研究[J]. 机械工程师,2006(9):65-67.

[2] 吴宇燕,彭志牛,王宇晗.NURBS曲线数控插补方法及误差控制[J].机械设计与研究,2006,22(4):75-78.

[3] 卜凡,樊留群,齐党进.数控加工速度前瞻及插补算法的研究[J].机械与电子,2013(8):44-47.

[4] 胡磊,林示麟,徐建明,等.S曲线加减速速度控制新方法[J].组合机床与自动化加工技术,2010(1):22-26,34.

[5] 郭新贵,李从心.S曲线加减速算法研究[J].机床与液压,2002(5):60-62.

[6] 李加文,陈宗雨,李从心.基于函数逼近的三角函数加减速方法[J].机床与液压,2006(3):66-67,8.

[7] 叶佩青,赵慎良.微小直线段的连续插补控制算法研究[J].中国机械工程,2004(15):1354-1356.

[8] 张得礼,周来水.数控加工运动的平滑处理[J].航空学报,2006,27(1):125-130.

[9] Erkorkmaz K,Altintas Y.High speed CNC system design. Part I:jerk li mited trajectory generation and quantic spline interpolation[J].International Journal of Machine Tools & Manufacture, 2001, 41(9):1323-1345.

[10] Jeon J W. A generalized approach for the acceleration and deceleration of CNC machine tools[C].CA,USA:IEEE IECON, International Conference on Industrial Electronics, Control and Instrumentation,1996.

[11] 尹涓,罗福源.插补前加减速运动时间周期化等效变换算法[J].中国机械工程,2014(24):3320-3325.

[12] 马永超.一种五段S曲线加减速算法的研究[J]. 工业控制计算机,2014(12):60-61.

[13] 田军锋,林浒,姚壮,等.数控系统S型曲线加减速快速规划研究[J].小型微型计算机系统,2013,34(1):168-172.

[14] 罗钧,汪俊,刘学明,等.基于S型加减速的自适应前瞻NURBS曲线插补算法[J].计算机集成制造系统,2013,19(1):55-60.

Research of S Curve Acceleration and Deceleration Control Algorithm Based on Matlab

HU Yongan，CHEN Caifeng，YANG Meng

(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai200093, China)

When the profile line of numerical control machining is broken line, the angle between the two path sections makes that it is necessary to take acceleration and deceleration control on the inflection point so as to make sure the trajectory precision. At present, we have many control methods of single coordinate motion by numerical control machining, among which the acceleration and deceleration control method based on S curve is the representative one. This thesis, on the basis of S-type acceleration and deceleration control curve, develops a new algorithm of S curve acceleration and deceleration control. With this new algorithm, we get a mathematical model of path sections geometric elements and the relation between allowable velocity and angle. We also draw that the transition velocityViofipath section is affected by turning vector angle ai, turning velocity ofi-1 andi+1 path sections, and path lengths ofiandi+1 path sections. Simulation of programming on the basis of Matlab leads to the changes of the corresponding coordinate velocity passing the point of broken lines, when the angles of the two adjacent broken lines are 90° and 135°.

S curve; transition velocity; angle; Matlab

2016- 05- 05

胡永安(1991-)，男，硕士研究生。研究方向：机械制造及其自动化。

10.16180/j.cnki.issn1007-7820.2017.04.015

TP273

A

1007-7820(2017)04-060-05