借你一双慧眼辨错

借你一双慧眼辨错

李胜军

幂的运算有：（1）同底数幂的乘法；（2）幂的乘方；（3）积的乘方；（4）同底数幂的除法.这些运算的数学式子及法则“相似度”较高，同学们极易出错.另外，整式加法运算中的项如果是幂的形式，也容易与幂的运算发生混淆.现将幂的运算中一些常见的错误加以剖析，希望同学们能拥有一双“慧眼”.

一、忽视指数1

例1计算：x5∙x4∙x.

错解：x5∙x4∙x=x5+4=x9.

剖析：错解认为算式x5∙x4∙x中的因式x的指数是0而出错.

正解：x5∙x4∙x=x5+4+1=x10.

说明：字母的指数为1时可省略不写，但在进行幂的运算时，必须还原出指数1参与计算.

二、运算法则“张冠李戴”

例2计算：y2∙y4.

错解：y2∙y4=y2×4=y8.

剖析：算式y2∙y4表示同底数幂的乘法，运算法则是“底数不变，指数相加”，错解误认为是“指数相乘”而出错.

正解：y2∙y4=y2+4=y6.

说明：进行幂的运算，先要弄清楚算式表示的运算，然后再根据相应的法则进行计算.本题错解将同底数幂的乘法法则与幂的乘方法则混淆了.

例3计算：m9÷m3.

错解：m9÷m3=m9÷3=m3.

剖析：算式m9÷m3表示同底数幂的除法，运算法则是“底数不变，指数相减”.错解误认为是“指数相除”而出错.

正解：m9÷m3=m9-3=m6.

说明：幂的运算要比相应法则中指数运算高一级.例如：同底数幂的乘法法则中“指数相加”（幂乘法→指数加法）；同底数幂的除法法则中“指数相减”（幂除法→指数减法），幂的乘方法则中“指数相乘”（幂乘方→指数乘法）.

例4计算：（a3）4.

错解：（a3）4=a3+4=a7.

剖析：算式（a3）4表示幂的乘方，运算法则是“底数不变，指数相乘”，错解错在误用了同底数幂的乘法法则进行计算.

正解：（a3）4=a3×4=a12.

说明：同底数幂的乘法与幂的乘方极易混淆，同学们要注意区分.

三、同底数幂的乘法与整式加法混淆

例5计算：a3∙a3.

错解：a3∙a3=2a3.

剖析：错解将同底数幂的乘法运算与整式加法运算混淆了，错用了整式加法的运算法则（合并同类项）.

正解：a3∙a3=a3+3=a6.

说明：如果不清楚算式表示的运算，有时也会将底数相同的整式加法运算误用同底数幂的乘法法则进行计算.例如：将x4+x4计算为x8就是错的.事实上，这里的x4+x4应进行合并同类项，即x4+x4=2x4.

四、积的乘方出现遗漏

例6计算：（-3xy4）3.

错解：（-3xy4）3=-3x3（y4）3=-3x3y12.

剖析：算式（-3xy4）3表示积的乘方，运算法则是“把积中的每一个因式分别乘方，再把所得的幂相乘”，错解只将积中字母部分进行了乘方，漏掉了积中系数的乘方.

正解：（-3xy4）3=（-3）3x3（y4）3=-27x3y12.

说明：积的乘方运算中，如果底数含有的因式较多，一定要注意将每个因式进行乘方，防止遗漏.

五、积的乘方系数出错

例7计算：（3a2b）2.

错解：（3a2b）2=32（a2）2b2=6a4b2.

剖析：错解中将系数与指数相乘而出错.

正解：（3a2b）2=32（a2）2b2=9a4b2.

说明：幂的指数与底数之间不存在任何运算关系，幂的指数表示乘方运算中底数的个数.例如：32中指数2表示乘方运算中底数3有两个，即32=3×3.

六、运算顺序出错

例8计算：210÷24÷24.

错解：210÷24÷24=210÷1=210.

剖析：算式210÷24÷24应按从左到右的顺序依次进行计算，错解运算顺序出错.

正解：210÷24÷24=210-4÷24=26÷24=26-4=22=4.

说明：同级运算，要按照从左到右的顺序依次进行计算.

七、符号出错

例9化简（-a2）3的结果是（）.

A.-a5B.a5C.-a6D.a6

错解：选D.

剖析：（-a2）3=［（-1）∙a2］3=（-1）3∙（a2）3

=-a6.错解中误认为-a2=（-a）2=a2导致出错.事实上-a2=（-1）∙a2.

正解：选C.

说明：防范幂的运算中符号出错的关键是正确判断底数中是否含有负号“-”.

八、分不清底数

例10计算：-x3∙（-x4）∙（-x）5.

错解：-x3∙（-x4）∙（-x）5=（-x）3+4+5=（-x）12=x12.

剖析：错解没有分清算式中各个因式的底数，误把三个因式的底数都认为是-x而出错.实际上，因式-x3表示x3的相反数，它的底数是x；因式-x4表示x4的相反数，它的底数是x；因式（-x）5表示-x的5次方，它的底数是-x.

正解：-x3∙（-x4）∙（-x）5=-x3∙（-x4）∙（-x5）=-x3∙x4∙x5=-x3+4+5=-x12.

说明：对于形如-xm、（-x）n（m、n都为整数）的幂的运算，常将底数统一为x再计算.计算时先确定结果的符号，然后再进行同底数幂的运算.

九、错用负整数指数幂

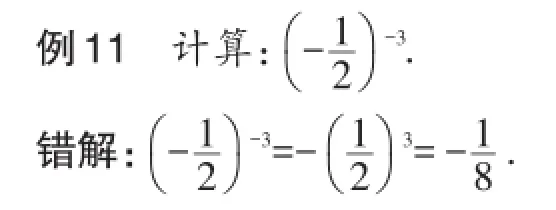
剖析：错解误用了负整数指数幂的性质，没有将底数取倒数.

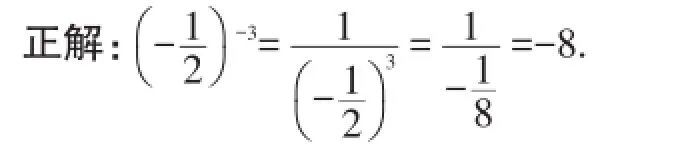
说明：运用负整数指数幂法则时，可按“底倒指反”进行，即底数取原底数的倒数，指数为原指数的相反数.

十、综合计算出错

例12计算：-x2∙（-x2）2-（-2x2）3.

剖析：错解在计算（-2x2）3时，字母部分的乘方是正确的，错在系数的乘方，误认为（-2）3=-6.

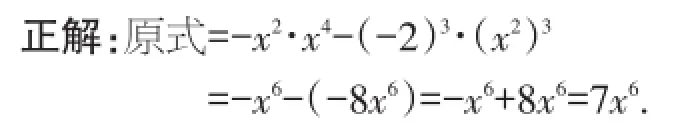
说明：本题综合了同底数幂的乘法、幂的乘方、积的乘方、整式的加减等多种运算，计算时要分清每一种运算，运用相应的法则进行计算.

江苏省盐城市北蒋实验学校）