带有斜撑的钢桁架数值简化分析及抗震性能*

王占飞， 陈小军， 金霞宇， 姜 丹

(沈阳建筑大学 a.交通工程学院， b.土木工程学院， 沈阳 110168)

带有斜撑的钢桁架数值简化分析及抗震性能*

王占飞a， 陈小军a， 金霞宇a， 姜 丹b

(沈阳建筑大学 a.交通工程学院， b.土木工程学院， 沈阳 110168)

为了探究带有斜撑的钢桁架结构简化分析及抗震性能，基于有限元软件ABAQUS6.10平台，对以往试验中的试件进行模型简化分析.利用位移延性系数和等效粘滞阻尼系数来评价该结构的抗震性能，数值分析中普通支撑采用B31梁单元，屈曲约束支撑采用T3D2桁架单元.结果表明，采用T3D2桁架单元模拟屈曲约束支撑，采用B31梁单元模拟普通支撑是合理的.通过考察结构的滞回性能、延性系数及等效粘滞阻尼系数，表明带有屈曲约束支撑的钢桁架结构具有良好的抗震性能.

桁架结构；屈曲约束支撑；模型简化；数值模拟；抗震性能；滞回曲线；屈曲；延性

在现代建筑及桥梁结构中支撑被广泛地用于提高结构的抗侧刚度和整体稳定性.然而普通支撑在地震作用下存在着受压屈曲的缺陷[1]，当支撑屈曲后，刚度和承载能力急剧下降，耗能能力较差[2].1994年的北岭地震和1995年的阪神地震震害调查表明，由于普通支撑的反复受压屈曲从而导致震害的加剧.防屈曲支撑(bucking restrained brace，简称BRB)是对普通支撑性能的改善，通过在芯材的外部设置套筒，解决了普通支撑受压屈曲以及滞回性能差的问题，使支撑无论受拉还是受压都能够达到屈服，表现出良好的力学性能.通过合理的设计，在罕遇地震发生时，BRB能够首先达到屈服，利用其滞回消耗地震能量，保护主体结构不被破坏.

目前，对屈曲约束支撑的研究多基于试验方面.顾炉忠、赵俊贤、严红和吴徽等通过拟静力试验来验证屈曲约束支撑具有良好的滞回性能和抗震性能[3-6]；李帼昌等对布置屈曲约束支撑的框架结构进行静力弹塑性分析，所得结果具有良好的抗震性能[7]；万金国、尹绕章等采用ABAQUS中的实体单元模拟屈曲约束支撑来研究其受力机理[8-9].由于缺少对屈曲约束支撑合理简化方面的研究，造成分析模型的单元数量过多，相互作用复杂，对计算机性能有较高的要求，不适用于整体结构的分析及结构设计.

因此，本文基于大型通用有限元软件ABAQUS6.10对试验中的结构进行简化建模，通过数值模拟结果与试验结果进行分析比较，验证此种简化方式的合理性，并提出一种简化建模的方法，在此基础上探究桁架结构的抗震性能.

1 试验概况

试验试件如图1所示(单位：mm).平面钢桁架的长度为1 600 mm，高度为800 mm.桁架结构左右两端为销栓连接，中间为滚轴连接的2次超静定结构.3根竖杆上分别作用有竖直方向轴力V，V为固定值，在上弦杆的右端部施加有往复作用的水平力H，用来模拟地震作用时的惯性力.3个试件的参数如表1所示.试件名称的第一段A、B、BRB表示支撑的类型，A、B支撑端部通过10 mm厚的连接板与上下弦杆和竖杆相连，支撑截面宽度分别为50、30 mm，支撑截面如图2a、b所示(单位：mm)；BRB是由芯材和外部套筒加上填充材料组成，如图2c所示(单位：mm).

图1 试验试件Fig.1 Specimen for test

表1 试件几何参数Tab.1 Geometric parameters for specimens

注：b为支撑截面宽度；As为支撑截面面积；PL为平面钢板；cy为往返加载.

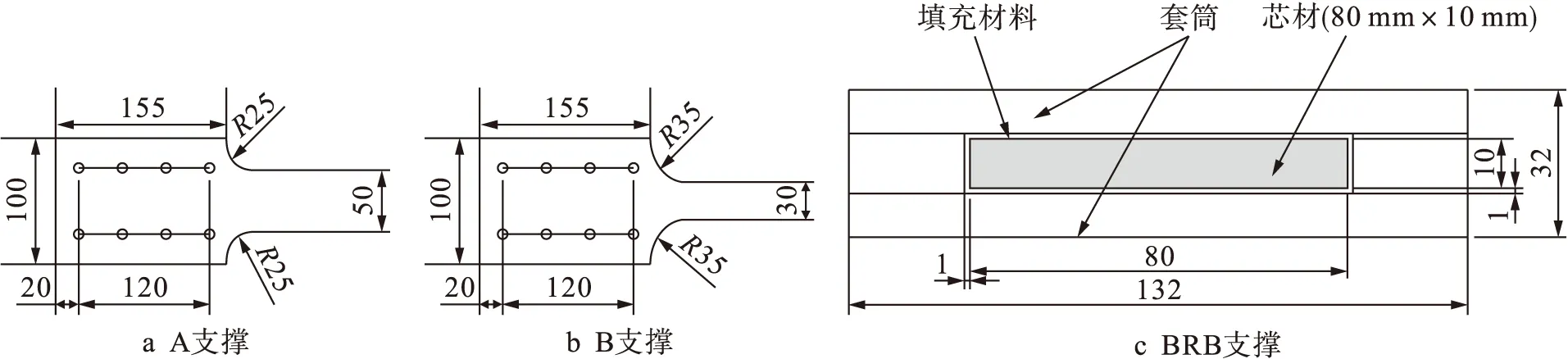
图2 支撑截面Fig.2 Sections of braces

2 有限元分析

2.1 分析模型

有限元分析模型的立面图如图3所示.除BRB外，3个试件的所有弦杆均采用B31单元，上下弦杆及竖杆均划分为10个单元，节点区域划分为4个单元，A、B支撑划分为8个单元，BRB采用T3D2单元进行模拟，划分为1个单元.考虑支座的影响，在节点F、D下端分别设置210 mm的刚体.图3中各个节点均为刚接，采用位移控制在C点施加水平往复荷载H，边界条件如表2所示.

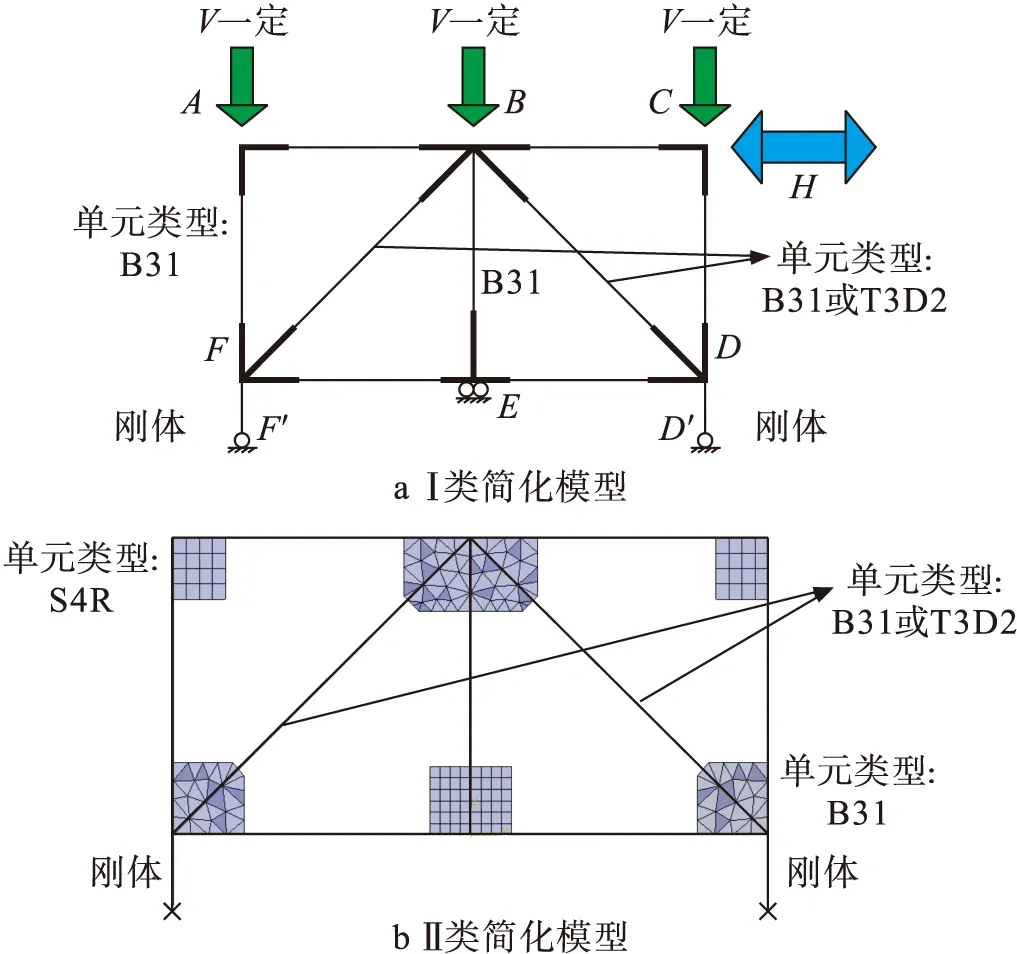
图3 有限元分析模型Fig.3 Finite element analysis model

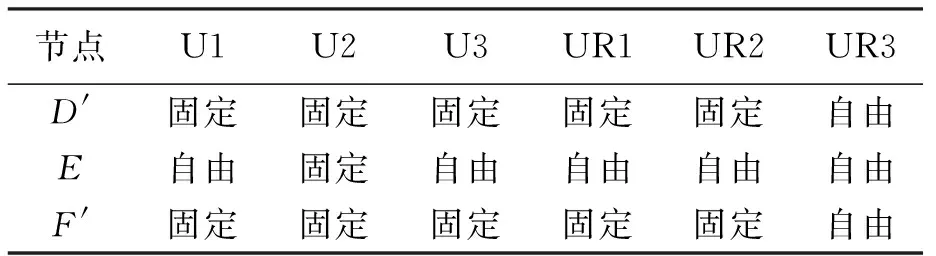
表2 有限元模型的边界条件Tab.2 Boundary conditions for finite element model

注：U1、U2、U3分别为x、y、z方向的平动；UR1、UR2、UR3分别为x、y、z方向的转动.

节点区域采用以下两类简化方式：Ⅰ类简化采用B31梁单元，通过加大梁截面翼缘厚度(图3a中黑色粗实线，厚度为17.6 mm)，考虑节点区域的强化，如图3a所示；Ⅱ类简化采用B31梁单元和S4R壳单元(壳单元的厚度为10 mm)，壳单元与梁单元之间采用绑定约束，如图3b所示.

2.2 材料属性

本文模型中用到两种型号的钢材，即SS400和SM400.SM400型号钢材用于BRB，其余部件的材料属性均为SS400.材料的力学性能如表3所示.钢材的本构关系为考虑包辛格效应的二折线随动强化的本构关系模型，二期刚度为初期刚度的1/100.

表3 材料的力学性能参数Tab.3 Mechanical performance parameters of materials

注：E为弹性模量；σy为屈服应力；σu为极限应力；υ为泊松比.

3 有限元分析与试验结果对比

3.1 有限元分析与试验滞回曲线

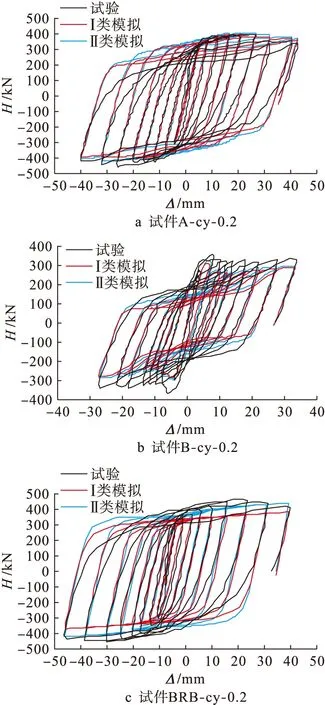
图4 桁架结构水平力水平位移滞回曲线Fig.4 Horizontal force-horizontal displacement hysteresis curves for steel truss structure

3.2 支撑的轴力与变形滞回性能

由于结构为对称结构，外部荷载也为对称荷载，左右支撑的受力反对称，模拟结果与理论结果一致，取左边支撑的轴力变形曲线进行分析.斜撑轴力N与轴向位移U的滞回曲线如图5所示.

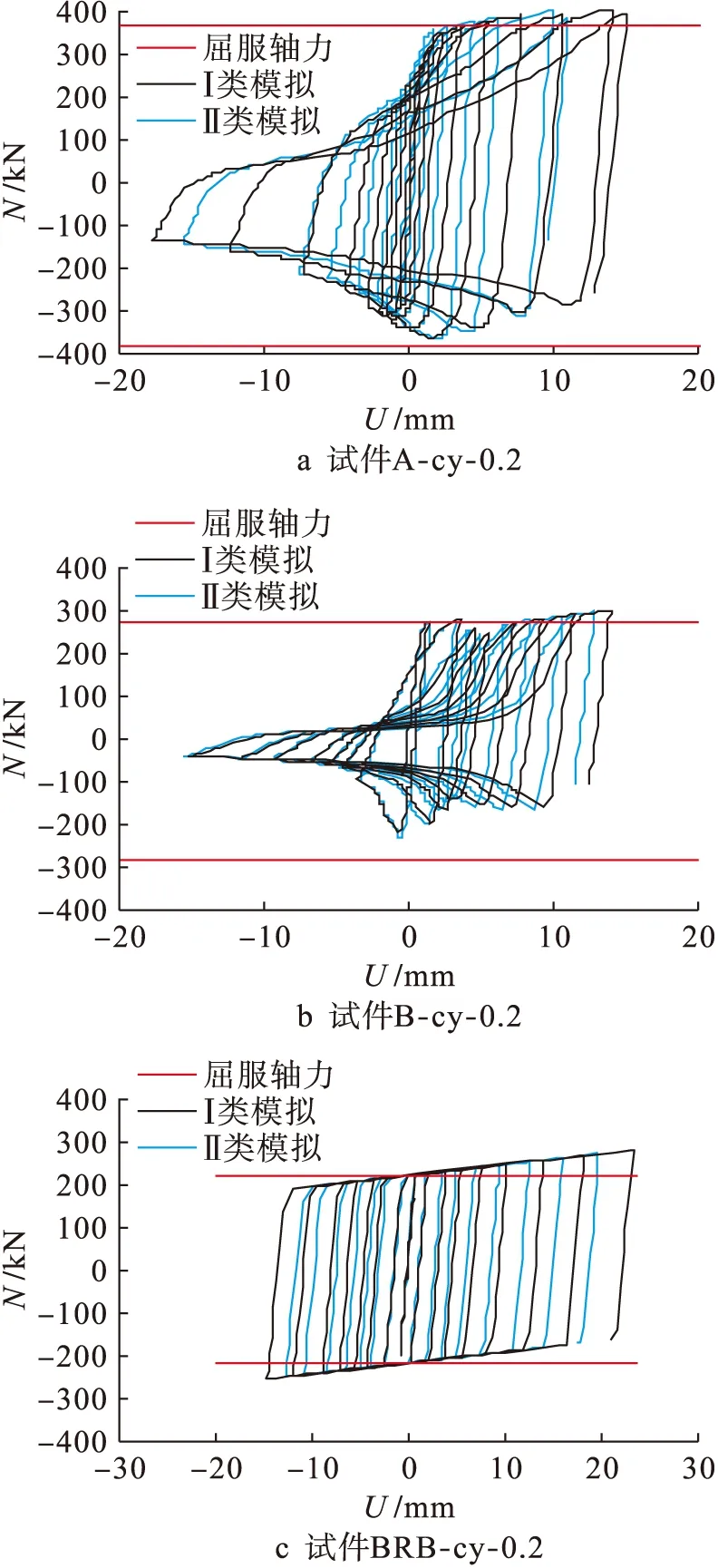
图5 斜撑轴力轴向位移滞回曲线Fig.5 Axial force-axial displacement hysteresis curves for diagonal braces

从图5中可以看出，支撑A和B的支撑轴力与变形滞回曲线不对称，支撑受拉时可以达到材料的屈服强度，受压时未能达到屈服强度，且支撑B受压时的力学性能很差.当支撑的轴力远未达到屈服轴力时，支撑受压屈曲，刚度和承载能力急剧下降，延性和耗能能力差.通过对支撑A和B的滞回曲线进行比较可以得出，支撑A通过增加截面面积延缓了其屈曲的发生.试件BRB-cy-0.2的轴力与变形滞回曲线呈现对称性，受拉、受压时材料均能达到屈服强度，充分利用材料的力学性能，具有很好的延性和耗能能力.在Ⅱ类简化方式情况下，支撑的轴向变形小于Ⅰ类简化方式，这是由于壳单元增加了对支撑的约束作用.3个试件的轴力和变形的有限元分析结果与实际构件的滞回性能一致，结果表明，用B31梁单元来模拟普通支撑，用T3D2桁架单元模拟屈曲约束支撑，可以较好地体现支撑在实际结构中的作用.

3.3 试件的变形

在最后一级循环加载过程中，以试件B-cy-0.2的变形为例，如图6a所示.在相同条件下有限元分析中试件B-cy-0.2的变形如图6b、c所示.从图6中可以看出，有限元分析结果与试验结果的形态相一致，说明用B31梁单元可以较好地模拟支撑受压屈曲的行为，同时也表明节点区域采用的两种简化模型对支撑屈曲变形的扩展影响较小.综上可知，模型简化及有限元分析模型设置是合理有效的.

4 抗震性能分析

本文采用位移延性系数和等效粘滞阻尼系数来评价结构的抗震性能，具体参数如表4所示.表4中位移延性系数等于极限承载力与屈服承载力的比值.屈服位移为钢材第一次进入塑性变形时的加载位移，极限位移取最大承载力所对应的位移.等效粘滞阻尼系数等于能量耗散系数除以2π.以Ⅱ类简化模型的有限元分析结果为例，从表4可以看出，试件BRB-cy-0.2的位移延性系数和等效粘滞阻尼系数均大于另外两个试件，这是由于屈曲约束支撑克服了普通支撑受压屈曲的问题，使构件在受拉和受压时都可以达到材料的屈服强度，充分利用了材料的力学性能，具有良好的延性和耗能能力，体现了采用屈曲约束支撑的结构具有良好的抗震性能.同时，试件A-cy-0.2的延性系数和等效粘滞阻尼系数大于试件B-cy-0.2是由于试件A-cy-0.2通过增加支撑截面面积增大了支撑受压时的临界荷载.

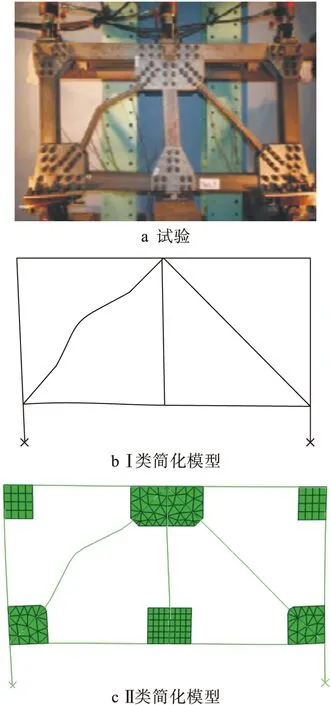
图6 试件B-cy-0.2的变形Fig.6 Deformation of specimen B-cy-0.2

表4 试件结构参数Tab.4 Parameters for specimens structure

5 结 论

本文通过分析得出以下结论：

1) 在对结构进行有限元分析时，用ABAQUS中T3D2桁架单元和B31梁单元分别模拟屈曲约束支撑和普通支撑可以较好地体现支撑在结构中的受力行为.

2) 节点区域用B31梁单元和S4R壳单元简化，均可以较好地体现支撑的受力行为.S4R壳单元较B31梁单元对结构的承载能力有所改善，在模型不复杂的情况下，建议用S4R壳单元来简化节点区域.

3) 带有屈曲约束支撑的钢桁架结构具有良好的塑性变形能力和耗能能力，抗震性能优越.

[1]汪家铭，中岛正爱.屈曲约束支撑体系的应用与研究进展(Ⅰ) [J].建筑钢结构进展，2005，7(1)：1-12.

(WANG Jia-ming，NAKASHIMA Masayoshi.The practice and research development of buckling restrained braced frames (Ⅰ) [J].Progress in Steel Building Structures，2005，7(1)：1-12.)

[2]郭彦林，刘建彬，蔡益燕，等.结构的耗能减震与防屈曲支撑 [J].建筑结构，2005，35(8)：18-23.

(GUO Yan-lin，LIU Jian-bin，CAI Yi-yan，et al.Structural energy dissipation and seismic mitigation method and buckling-restrained brace [J].Building Structure，2005，35(8)：18-23.)

[3]顾炉忠，高向宇，徐建伟，等.防屈曲支撑混凝土框架结构抗震性能试验研究 [J].建筑结构学报，2011，32(7)：101-111.

(GU Lu-zhong，GAO Xiang-yu，XU Jian-wei，et al.Experimental research on seismic performance of BRB concrete frames [J].Journal of Building Structures，2011，32(7)：101-111.)

[4]赵俊贤，吴斌，欧进萍.新型全钢防屈曲支撑的拟静力滞回性能试验 [J].土木工程学报，2011，44(4)：60-70.

(ZHAO Jun-xian，WU Bin，OU Jin-ping.Uniaxial quasi-static cyclic tests on the hysteretic behavior of a novel type of all-steel buckling-restrained brace [J].China Civil Engineering Journal，2011，44(4)：60-70.)

[5]严红，潘鹏，王元清，等.一字形全钢防屈曲支撑耗能性能试验研究 [J].建筑结构学报，2012，33(11)：142-149.

(YAN Hong，PAN Peng，WANG Yuan-qing，et al.Experimental study of buckling-restrained braces with in-line steel core plate encased in double web wide flange steel outer unit [J].Journal of Building Structures，2012，33(11)：142-149.)

[6]吴徽，张艳霞，张国伟，等.防屈曲支撑作为可替换耗能元件抗震性能试验研究 [J].土木工程学报，2013，46(11)：29-36.

(WU Hui，ZHANG Yan-xia，ZHANG Guo-wei，et al.Experimental study on seismic performance of replaceable buckling-restrained braces in reinforced concrete frame [J].China Civil Engineering Journal，2013，46(11)：29-36.)

[7]李帼昌，张迎，高成富，等.BRB-钢管高强混凝土结构的抗震性能分析 [J].沈阳工业大学学报，2012，34(5)：591-595.

(LI Guo-chang，ZHANG Ying，GAO Cheng-fu，et al.Seismic resistance analysis on BRB-high strength concrete-filled steel tube structure [J].Journal of Shen-yang University of Technalogy，2012，34(5)：591-595.)

[8]万金国，杨凡，李文峰，等.双屈服点免断裂屈曲约束支撑性能试验与数值模拟 [J].建筑结构，2013，43(17)：105-108.

(WAN Jin-guo，YANG Fan，LI Wen-feng，et al.Experiment research and mechanical simulation of BRB with double yield points and non-fracture [J].Building Structure，2013，43(17)：105-108.)

[9]尹绕章，邓雪松，周云.新型钢板装配式屈曲约束支撑有限元分析 [J].地震研究，2014，37(2)：288-292.

(YIN Rao-zhang，DENG Xue-song，ZHOU Yun.Finite element analysis of novel steel-plate assembled buckling-restrained brace [J].Journal of Seismological Research，2014，37(2)：288-292.)

(责任编辑：钟 媛 英文审校：尹淑英)

Numerical simplified analysis and seismic performance of steel truss with diagonal braces

WANG Zhan-feia,CHEN Xiao-juna,JIN Xia-yua,JIANG Danb

(a.School of Traffic Engineering,b.School of Civil Engineering,Shenyang Jianzhu University,Shenyang 110168,China)

In order to explore the simplified analysis and seismic performance of steel truss with diagonal braces,the simplified analysis for the samples from the previous experiments was carried out based on the finite element software ABAQUS6.10 platform.The seismic performance of the structure was evaluated with the displacement ductility coefficient and equivalent viscous damping coefficient.In the numerical analysis,the B31 beam element was used for the ordinary braces,and the T3D2 truss element was used for the buckling restrained braces.The results show that it is reasonable to simulate the buckling restrained braces with the T3D2 truss element and to simulate the ordinary braces with the B31 beam element.Through studying the hysteretic behavior,ductility coefficient and equivalent viscous damping coefficient of the structure,it is noted that the steel truss structure with the buckling restrained braces has good seismic performance.

truss structure;buckling restrained brace;model simplification;numerical simulation;seismic performance;hysteresis curve;buckling;ductility

2016-03-30.

辽宁省高等学校杰出青年学者成长计划项目(LJK2014060).

王占飞(1976-)，男，辽宁法库人，副教授，博士，主要从事桥梁抗震等方面的研究.

22 17∶40在中国知网优先数字出版.

http：∥www.cnki.net/kcms/detail/21.1189.T.20161222.1740.036.html

10.7688/j.issn.1000-1646.2017.02.17

TU 391

A

1000-1646(2017)02-0213-06