考虑损失规避与产品质量水平的供应链协调契约模型
刘云志,樊治平
(1. 南京大学工程管理学院,江苏 南京 210093;2. 东北大学工商管理学院,辽宁 沈阳 110167)
考虑损失规避与产品质量水平的供应链协调契约模型
刘云志1,2,樊治平2
(1. 南京大学工程管理学院,江苏 南京 210093;2. 东北大学工商管理学院,辽宁 沈阳 110167)
供应链的整体协调和产品质量水平是取得供应链竞争优势的关键,因此关于考虑产品质量水平的供应链协调问题的研究是值得关注的。本文着重研究了考虑损失规避与产品质量水平的二级供应链协调问题,在零售商存在损失规避行为的假设下,依据Wang和Webster给出的损失规避效用函数刻画了零售商的损失规避行为,通过分析分别得到了分散式决策下供应商与损失规避型零售商的最优策略和集中式决策下供应链的最优策略,同时分析了二级供应链在批发价格契约下的协调情况,并构建了批发价格-质量成本分担契约下的供应链协调契约模型,且论证了该供应链协调契约模型的有效性。通过分析得到的主要结论是:在分散式决策下,供应商的产品质量水平为损失规避型零售商的订货量的严格递增函数,损失规避型零售商的订货量为供应商的产品质量水平的严格递增函数;在集中式决策下,供应商的产品质量水平为零售商的订货量的严格递增函数,零售商的订货量为供应商的产品质量水平的严格递增函数;批发价格契约不能协调此二级供应链;一定条件下批发价格-质量成本分担契约能够协调此二级供应链。此外,在分散和集中式决策下,通过数值实验分析了模型参数变化对最优产品质量水平与最优订货量的影响。所得研究结论对于相关供应链管理者或成员具有一定的参考价值。
供应链协调;损失规避;质量水平;契约模型
1 引言
实现供应链的整体协调是取得供应链竞争优势的关键,因此供应链协调已成为运作管理领域的热点研究问题之一。供应链契约主要包括批发价格契约、收益共享契约、数量折扣契约、回扣契约、回购契约、期权契约等[1-5]。通过合理的契约设计,有助于减少双重边际化和信息不对称等不利因素所带来的影响,从而提高供应链的整体利润,以致使供应链达到协调,并实现供应链竞争优势。同时,产品质量水平是实现供应链竞争优势的一个重要因素[6-7]。在一些特定的市场环境中,一些企业正将简单的价格竞争策略转向质量竞争策略[8,9],即这些企业采用相同的价格策略,但是提供不同质量水平的产品来进行合理的竞争,例如,在电信行业中,中国移动运营商与中国电信有限公司通过提供不同的增值功能服务和服务质量来吸引潜在的用户;在餐饮行业中,肯德基与麦当劳通过为顾客提供不同品种或口味的食品来进行竞争,故针对供应链中产品质量水平问题的研究受到了一些相关学者的关注[10-17]。综上所述,关于考虑产品质量水平的供应链协调契约模型的探索和理论分析是有必要的。
目前,可以看到一些国内外学者针对考虑产品质量水平的供应链协调契约模型的研究成果[18-23],例如,Gurnani和Erkoc[18]针对市场需求受产品质量水平与零售商促销努力水平共同影响的分销渠道协调问题,分析和比较了三种不同的供应链契约,并指出批发价格契约为一般特许经营契约的特殊形式,且当零售商保留效用与信息不对称程度过高时制造商更倾向于选择个人固定税费契约而不是一般特许经营契约;Ma Peng等[19]考虑了市场需求受零售商促销努力水平与产品质量水平共同影响的情形,针对由单一制造商与单一零售商组成的二级供应链协调问题,提出了一种新型契约来协调此二级供应链,并通过分析给出了最优销售努力水平、最优质量改进努力水平及最优供应链利润;Liu Weihua等[20]针对一个二级物流服务供应链,基于单周期质量协调模型,提出了一个多周期质量协调模型,并构建了一个三级物流服务供应链下的新型模型,最后通过仿真分析说明了多周期合作模式下当缺货惩罚低于确定临界值时物流集成商更倾向于做出快速的决策,在三级物流服务供应链下子服务集成商与终端物流服务提供商的均衡解与缺货惩罚成本无关;但斌等[21]考虑了产品的生产质量水平和销售质量水平同时影响顾客需求的情形,建立了制造商处于领导地位的二级供应链决策模型,分析了在分散式和集中式决策下制造商和零售商关于产品质量的决策,设计了一个成本分摊和收入共享契约来协调此二级供应链,并证明了这种契约可使制造商和零售商获得比分散式决策下更多的利润;胡军等[22]基于线性需求函数,针对四种不同的契约,比较了企业质量控制和供应链协调兼达时各契约模型的决策选择和收益,并证明了各种不同契约类型在供应链协调中的有效性,即传统批发价格契约不能实现供应链的协调,而收益共享契约、奖励惩罚契约和特许经营契约均能实现供应链协调;肖迪等[23]针对由两个供应商与一个制造商所构成的供应链系统,研究了质量竞争和价格竞争同时作用下的供应链成员的协调运作策略,并通过论证得到供应商合作有助于提升供应商的质量努力程度,但会导致供应链整体利润的下降,而质量竞争越激烈,在多数情景中供应商的质量努力程度就越高,但价格竞争的激烈程度对供应商努力程度的影响较为有限。上述研究成果的共同点是均假定供应链成员是风险中性的,但一些学者通过研究发现供应链成员有时并非按照这一原则进行决策[24,25]。此后,非风险中性假设条件下的供应链协调问题得到了一些学者的关注[26-28],并且Kahneman和Tversky[29]提出的前景理论常常被用来描述供应链成员的决策行为,前景理论中的一个重要结论是决策者是损失规避的。近年来,一些学者开始从供应链成员具有损失规避行为特征的视角,针对供应链协调问题展开研究[30-39]。但需要指出的是,同时考虑供应链成员的损失规避行为与产品质量水平的供应链协调契约模型的研究成果所见甚少。为此,本文则是在假定随机市场需求受供应商的产品质量水平影响的前提下,针对由一个风险中性的供应商与一个损失规避型零售商组成的二级供应链协调问题,分别讨论分散式决策下供应商与损失规避型零售商的最优策略和集中式决策下供应链的最优策略,同时分析二级供应链在批发价格契约下的协调情况,并构建批发价格-质量成本分担契约下的供应链协调契约模型,且论证该供应链协调契约模型的有效性,最后通过数值实验,分别分析模型参数变化对分散和集中式决策下最优产品质量水平与最优订货量的影响。
2 基本模型
2.1 问题描述与基本假设
考虑一个经营单一时令性产品的二级供应链,同Wang和Webster[31,40]的基本假设,与供应商的企业规模相比,零售商的企业规模往往较小,故供应商应是风险中性的,而零售商则是损失规避的,这里假设此二级供应链由一个风险中性的供应商与一个损失规避型零售商构成。进一步地,假设此二级供应链的所有信息是完全共享的,且供应商与零售商签订批发价格契约合同。
在销售季前,供应商依据批发价格契约以单位产品生产成本c生产相应的产品,并以单位产品批发价格w将此产品出售给零售商,且零售商的采购量为q;在销售季中,零售商以单位产品销售价格p销售产品给顾客,该产品的市场需求量D为一个随机变量,若在销售季中出现缺货情形,则零售商所承担的单位产品缺货成本为gr,供应商所承担的单位产品缺货成本为gs;在销售季末,若零售商仍有剩余的产品未被销售,则剩余产品将被统一进行季末处理,且单位剩余产品的净残值为v,不失一般性,假设在供应商方面处理的单位剩余产品的净残值不高于v,则剩余产品会由零售商进行季末处理。依据客观现实的合理性,则有p>w>c>v>0,gr,gs>0。
为了提高产品的销售量,供应商会通过一系列措施来提高产品的质量水平,这里假定产品质量水平为θ,θ∈[0,+∞),且供应商需要付出相应的努力成本来达到此产品质量水平,其中努力成本为产品质量水平θ的函数,记努力成本函数为f(θ)。在现实中,若产品质量水平越高,则供应商所付出的努力成本也就越高,故努力成本函数f(θ)是关于产品质量水平θ的严格递增函数,即f′(θ)>0,此外努力成本函数f(θ)应为关于产品质量水平θ的严格凸函数,即f″(θ)>0,表明努力成本函数f(θ)关于产品质量水平θ是边际递增的。特殊地,若供应商未对提高产品质量水平付出任何成本,则f(θ)=0。
2.2 模型构建
风险中性的供应商的利润为:
πs(q,θ)=wq-cq-gsmax{D-q,0}-f(θ)
(1)
依据式(1),可得到风险中性的供应商的期望利润为:
(2)
风险中性的零售商的利润为:
πr(q,θ)=pmin{D,q}+vmax{q-D,0}-wq-grmax{D-q,0}
(3)
依据式(3),可得到风险中性的零售商的期望利润为:
E(πr(q,θ))=(p+gr-w)q-(p+gr-v)
(4)
风险中性的零售商的利润为:
(5)
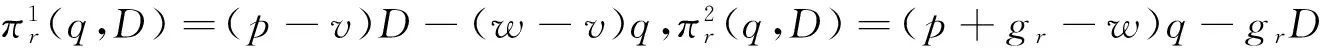
依据文献[40]的分析思想,通过分析可得到如下性质。
证明 设k为市场的实际需求值,则:
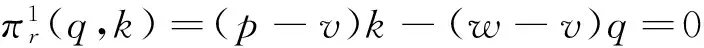
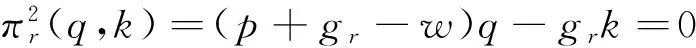
综上,若D
考虑如下形式的损失规避效用函数[40-41],即:
(6)
其中,W0为零售商的初始财富值,参数λ∈[1,+∞]表示零售商的损失规避程度。若λ=1,则表明零售商是风险中性的;若λ>1,则表明零售商是损失规避的,即此零售商为损失规避型零售商,且随着λ的增加,零售商损失规避的程度亦增加。为了讨论简便且不失一般性,这里假定W0=0,即零售商的初始财富值为0。
依据式(5)和(6),可得到损失规避型零售商的期望效用为:
E(μ(πr(q,θ)))=E(πr(q,θ))+(λ-1)
(7)
式(7)的经济学意义可被解释为:损失规避型零售商的期望效用为零售商在风险中性条件下所获得的期望利润与零售商在具有损失规避行为特征下的超订和缺货所遭受的期望损失之和。
3 供应链协调契约模型
本节分别讨论分散式决策下供应商与损失规避型零售商的最优策略和集中式决策下供应链的最优策略,同时分析二级供应链在批发价格契约下的协调情况,并在此基础上构建批发价格-质量成本分担契约下的供应链协调契约模型,且进一步论证该供应链协调契约模型的有效性。
3.1 分散式决策下供应商与损失规避型零售商的最优策略
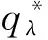
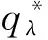
证明 对于∀θ∈(0,+∞),针对式(7)求关于q的一阶与二阶导数,即:
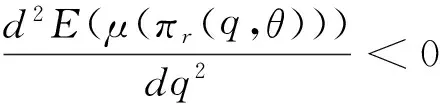
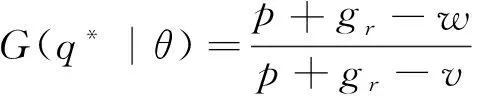
定理2 对于∀θ∈[0,+∞),有3种情况:
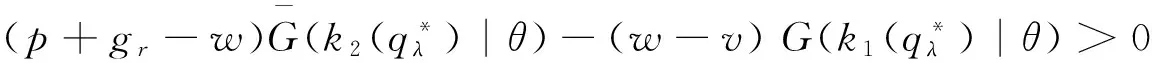
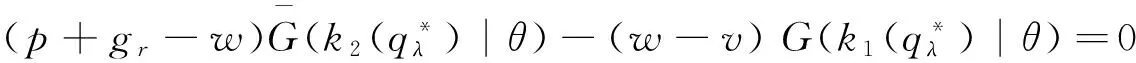
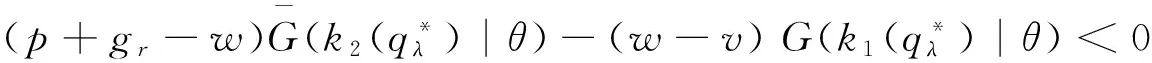
证明 对于∀θ∈(0,+∞),由定理1可知:
进一步整理得到:
即:
依据隐函数定理,则有:
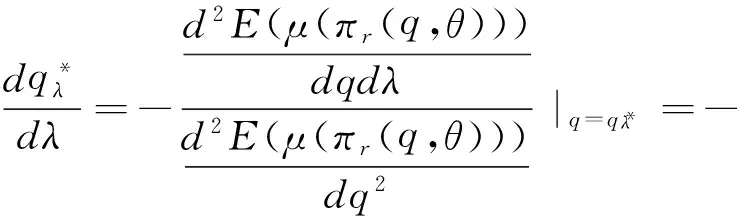
由于p-v>0,gr>0,λ>1,则:
进一步地可得到如下结论:
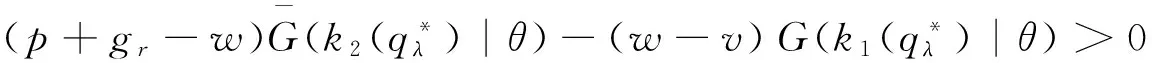
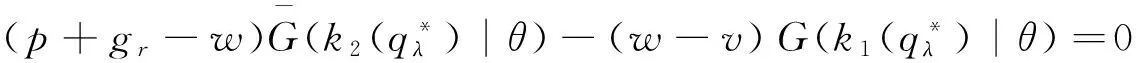
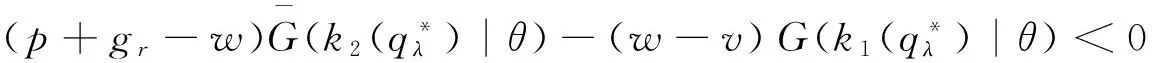
定理2揭示了在供应商的产品质量水平一定的情形下,损失规避型零售商的最优订货量与风险中性零售商的最优订货量之间的关系,同时也说明了在供应商的产品质量水平一定的情形下,损失规避型零售商的最优订货量与损失规避系数之间的关系。
依据式(2)和(7),供应商的产品质量水平的最优反应函数θ(q)与损失规避型零售商订货量的最优反应函数q(θ)应分别满足式(8)和(9),即:
(8)
(9)
定理3 在分散式决策下,供应商的产品质量水平的最优反应函数θ(q)是关于损失规避型零售商订货量q的严格递增函数,损失规避型零售商订货量的最优反应函数q(θ)是关于供应商的产品质量水平θ的严格递增函数。
证明 供应商的产品质量水平与损失规避型零售商订货量的最优反应函数θ(q)和q(θ)分别满足式(8)和(9),依据隐函数定理,则有:
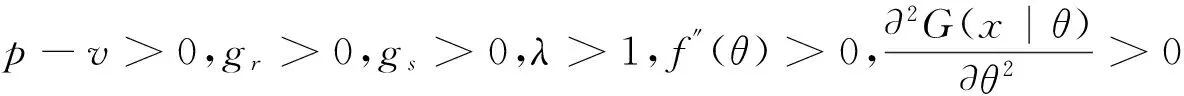
综上,供应商的产品质量水平的最优反应函数θ(q)是关于损失规避型零售商订货量q的严格递增函数;损失规避型零售商订货量的最优反应函数q(θ)是关于供应商的产品质量水平θ的严格递增函数。证毕。
定理3表明:在分散式决策下,损失规避型零售商订货量的提高能够促使相应供应商的产品质量水平的提高,供应商的产品质量水平的提高有助于损失规避型零售商订货量的提高。
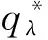
(10)
3.2 集中式决策下供应链的最优策略
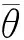
集中式决策下供应链的利润为:
π(q,θ)=pmin{D,q}+vmax{q-D,0}-(gr+gs)mas{D-q,0)-cq-f(θ)
(11)
依据式(11),可得到集中式决策下供应链的期望利润为:
(12)
(13)
(14)
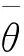
定理4的证明过程与定理3的证明过程类似,这里不再赘述。
定理4表明:在集中式决策下,零售商订货量的提高能够促使相应供应商的产品质量水平的提高,供应商的产品质量水平的提高有助于零售商订货量的提高。
(15)
定理5 考虑损失规避型零售商与产品质量水平的二级供应链在批发价格契约下无法达到协调。

即:
p+gr-v=0
由于p>v,gr>0,则p+gr-v≠0恒成立,故考虑损失规避型零售商与产品质量水平的二级供应链在批发价格契约下无法达到协调。证毕。
3.3 批发价格-质量成本分担契约下的供应链协调契约模型
基于上述分析可知,考虑损失规避型零售商与产品质量水平的二级供应链在批发价格契约下无法达到协调,故需要设计新的契约来协调此二级供应链,这里通过设计一种损失规避型零售商分担供应商部分努力成本的批发价格-质量成本分担契约来协调此二级供应链,即在批发价格契约下,损失规避型零售商分担一部分供应商为提高产品质量水平所付出的努力成本,且不妨假定成本分担系数为α,α∈(0,1),供应商分担的努力成本为αf(θ),损失规避型零售商分担的努力成本为(1-α)f(θ)。
在批发价格-质量成本分担契约下,供应商的期望利润和损失规避型零售商的期望效用分别为:
(16)
(17)
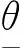
(18)
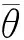
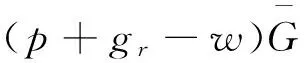
w=
w∈(c,p)
其中θ**和q**同时满足式(15)和(18)。
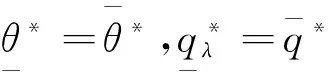

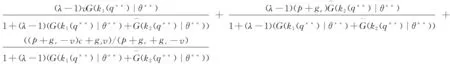
w∈(c,p) 证毕。
定理6的实际含义是:当考虑损失规避型零售商与产品质量水平的二级供应链达到协调时,成本分担系数与单位产品批发价格应满足的条件,且成本分担系数与单位产品的批发价格、生产成本以及损失规避系数无关,而单位产品批发价格不仅与模型中涉及的参数相关,而且还与供应商和损失规避型零售商的策略相关。定理6的管理启示是:从供应商的立场来看,供应商在拟定批发价格-质量成本分担契约合同时,可不必考虑单位产品的批发价格、生产成本以及损失规避系数对成本分担系数设计的影响,但要考虑模型中涉及的参数以及供应链成员的策略对单位产品批发价格设计的影响。定理6表明:在批发价格-质量成本分担契约下,考虑损失规避型零售商与产品质量水平的二级供应链可达到协调,这就说明了在批发价格-质量成本分担契约下供应链的整体利润可实现帕累托改进并达到协调,即说明了供应商与损失规避型零售商中至少有一方的利润是增加的。定理6的另一管理启示是:无论从供应商还是损失规避型零售商的立场来看,二者均更具意愿来签订批发价格-质量成本分担契约合同,且通过协商可实现供应链成员的双赢。
4 数值实验
为了说明上文提及模型的参数对分散和集中式决策下最优产品质量水平与最优订货量的影响,本文针对批发价格-质量成本分担契约下的供应链协调契约模型进行了相应的数值实验。
为了简化分析,这里假定市场需求函数D=θ1/2+δ,其中δ为随机变量且其概率分布函数与概率密度函数分别为H(x)和h(x),从而可以得到随机需求D的条件分布函数与条件概率密度函数分别为G(x|θ)=H(x-θ1/2)和g(x|θ)=h(x-θ1/2)。进一步地,假定随机需求D服从[0,100]上的均匀分布,则μ=50,努力成本函数f(θ)=μθ2/2=25θ2。依据客观现实的合理性,即p>w>c>v>0,gr,gs>0,在批发价格-质量成本分担契约下,供应链协调契约模型中涉及的一些参数取值为:p=30,w=25,c=15,gr=gs=5,v=10,λ=2,α=0.1。
本文的参数实验分析涉及8个方面,下面简要给出参数实验分析的有关说明及相关结论。
1)将单位产品销售价格p视为变量,进行相关的数值实验。考察参数p的变化(如考虑p从25变化到50)对分散和集中式决策下最优产品质量水平与最优订货量的影响,且参数实验分析结果如图1和2所示。由图1和2可知,随着单位产品销售价格的增加,最优产品质量水平与最优订货量在分散式决策下均是先增加后减少的,而在集中式决策下均是增加的。
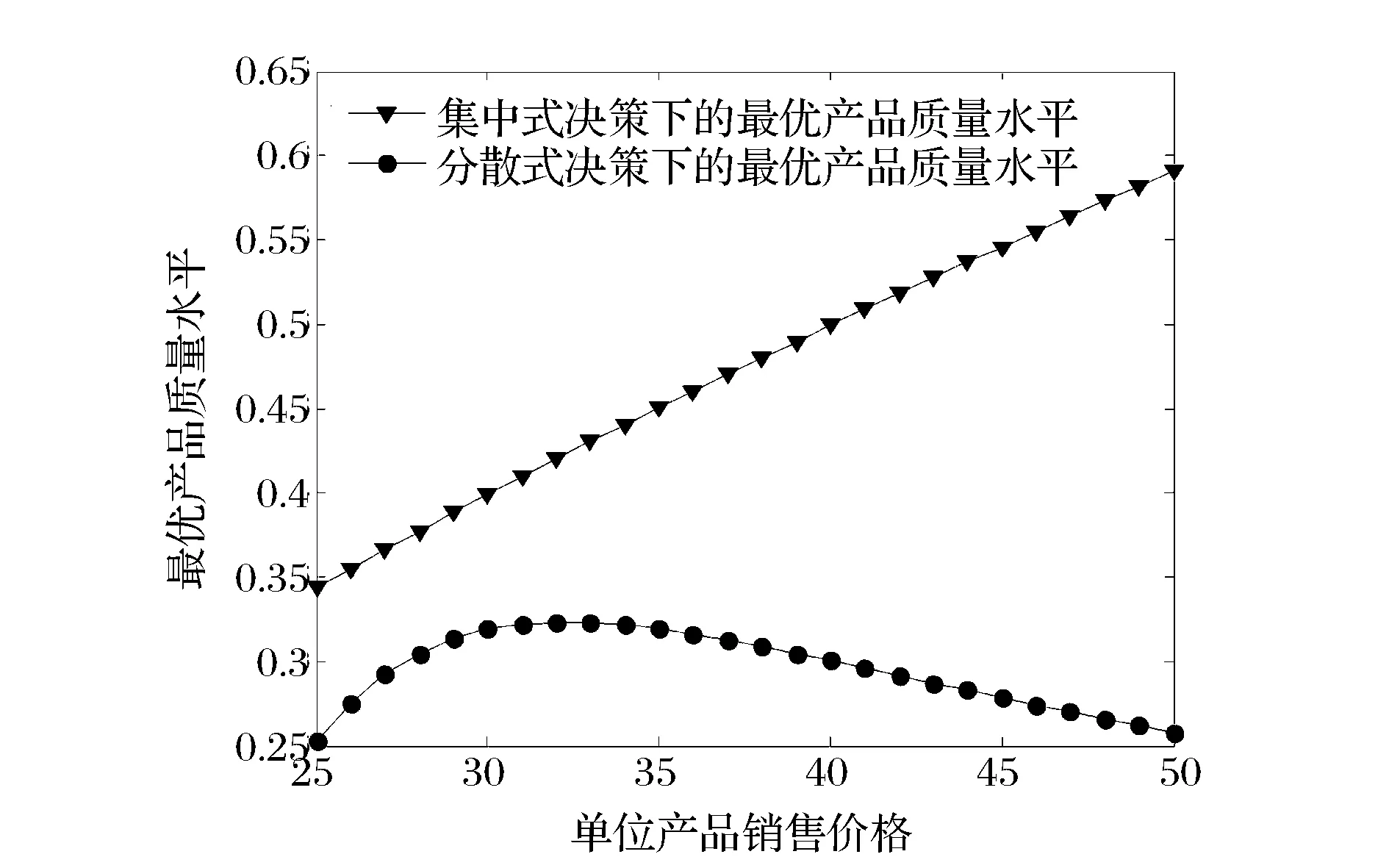
图1 单位产品销售价格对最优产品质量水平的影响
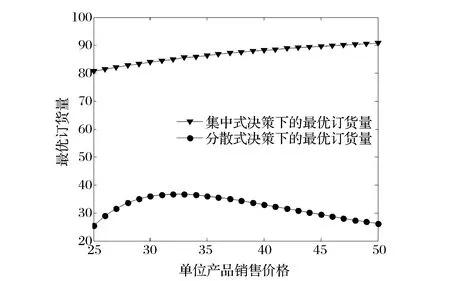
图2 单位产品销售价格对最优订货量的影响
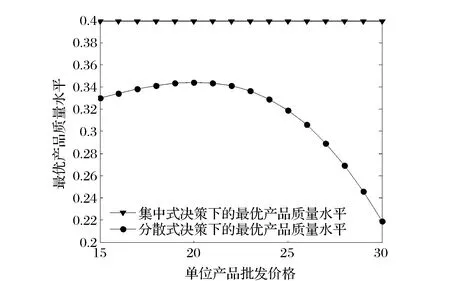
图3 单位产品批发价格对最优产品质量水平的影响
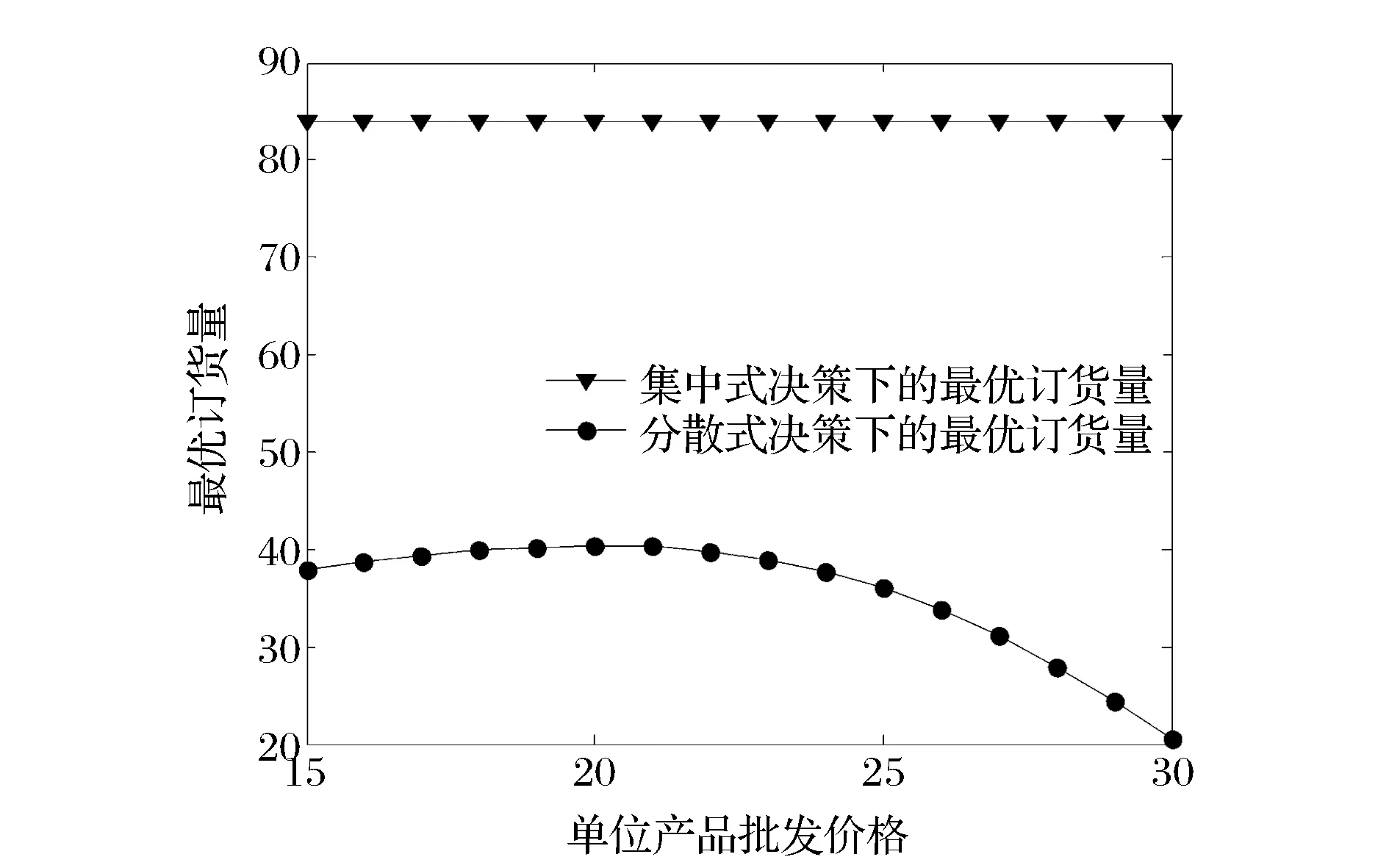
图4 单位产品批发价格对最优订货量的影响
2)将单位产品批发价格w视为变量,进行相关的数值实验。考察参数w的变化(如考虑w从15变化到30)对分散和集中式决策下最优产品质量水平与最优订货量的影响,且参数实验分析结果如图3和4所示。由图3和4可知,随着单位产品批发价格的增加,最优产品质量水平与最优订货量在分散式决策下均是先增加后减少的,而在集中式决策下均是不变的(式(15)不含参数w)。
3)将单位产品生产成本c视为变量,进行相关的数值实验。考察参数c的变化(如考虑c从10变化到25)对分散和集中式决策下最优产品质量水平与最优订货量的影响,且参数实验分析结果如图5和6所示。由图5和6可知,随着单位产品生产成本的增加,最优产品质量水平与最优订货量在分散式决策下均是不变的(式(18)不含参数c),而在集中式决策下均是减少的。
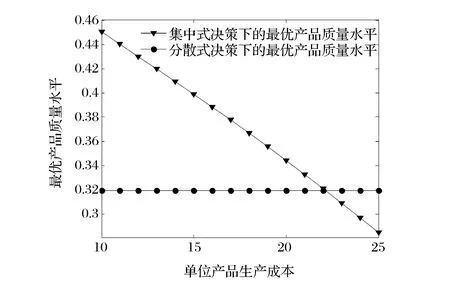
图5 单位产品生产成本对最优产品质量水平的影响
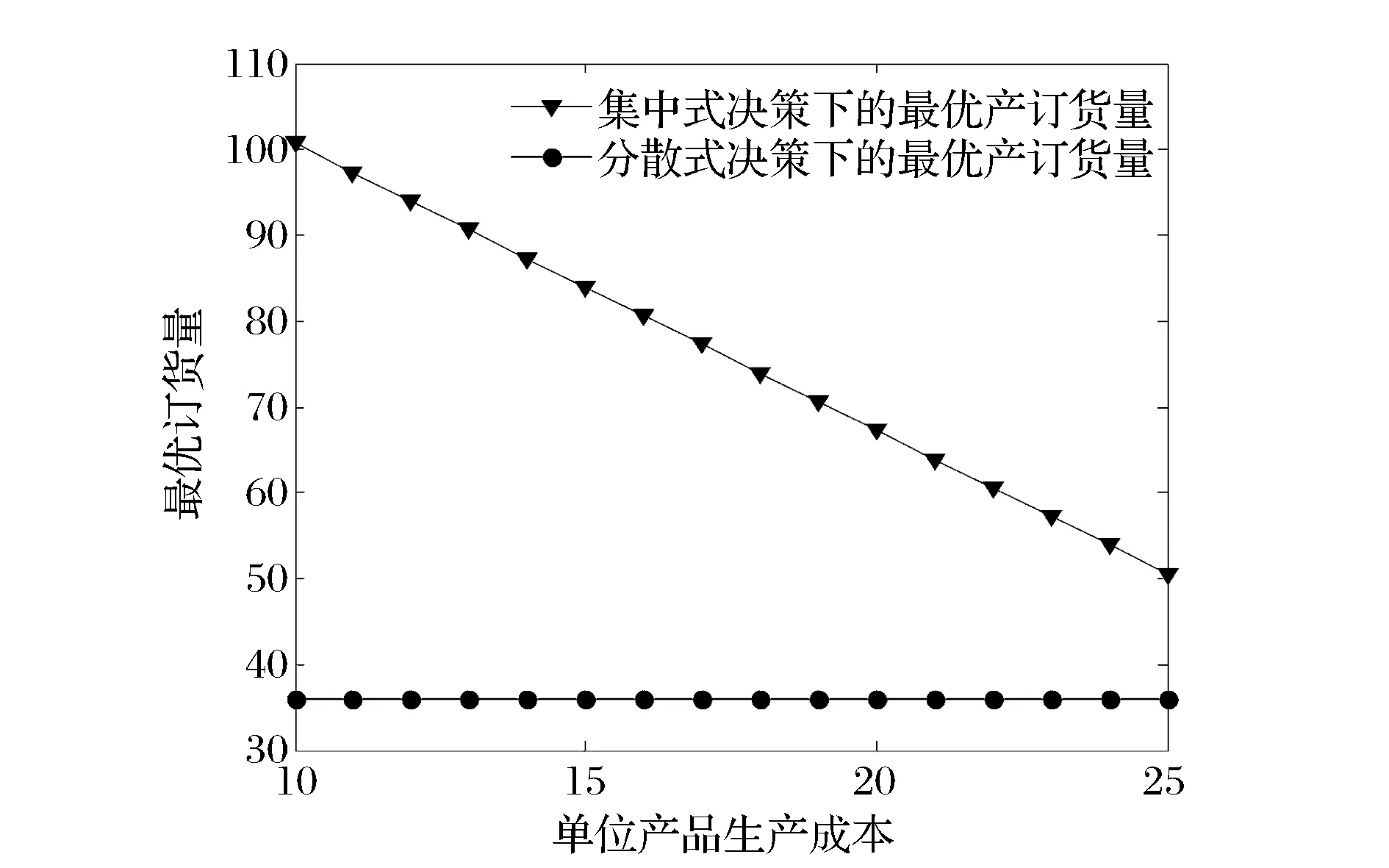
图6 单位产品生产成本对最优订货量的影响
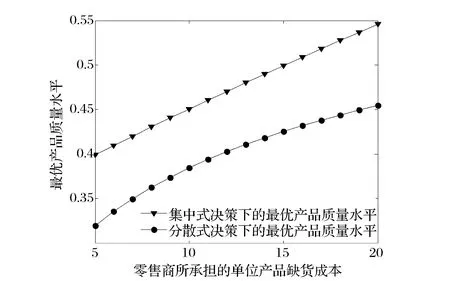
图7 零售商所承担的单位产品缺货成本对最优产品质量水平的影响
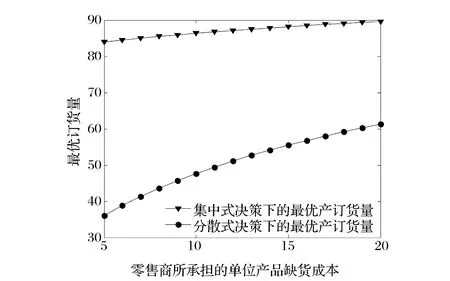
图8 零售商所承担的单位产品缺货成本对最优订货量的影响
4)将零售商所承担的单位产品缺货成本gr视为变量,进行相关的数值实验。考察参数gr的变化(如考虑gr从5变化到20)对分散和集中式决策下最优产品质量水平与最优订货量的影响,且参数实验分析结果如图7和8所示。由图7和8可知,随着零售商所承担的单位产品缺货成本的增加,最优产品质量水平与最优订货量在分散与集中式决策下均是增加的。
5)将供应商所承担的单位产品缺货成本gs视为变量,进行相关的数值实验。考察参数gs的变化(如考虑gs从5变化到20)对分散和集中式决策下最优产品质量水平与最优订货量的影响,且参数实验分析结果如图9和10所示。由图9和10可知,随着供应商所承担的单位产品缺货成本的增加,最优产品质量水平与最优订货量在分散与集中式决策下均是增加的,且在分散式决策下的最优订货量的变化相对不敏感。

图9 供应商所承担的单位产品缺货成本对最优产品质量水平的影响
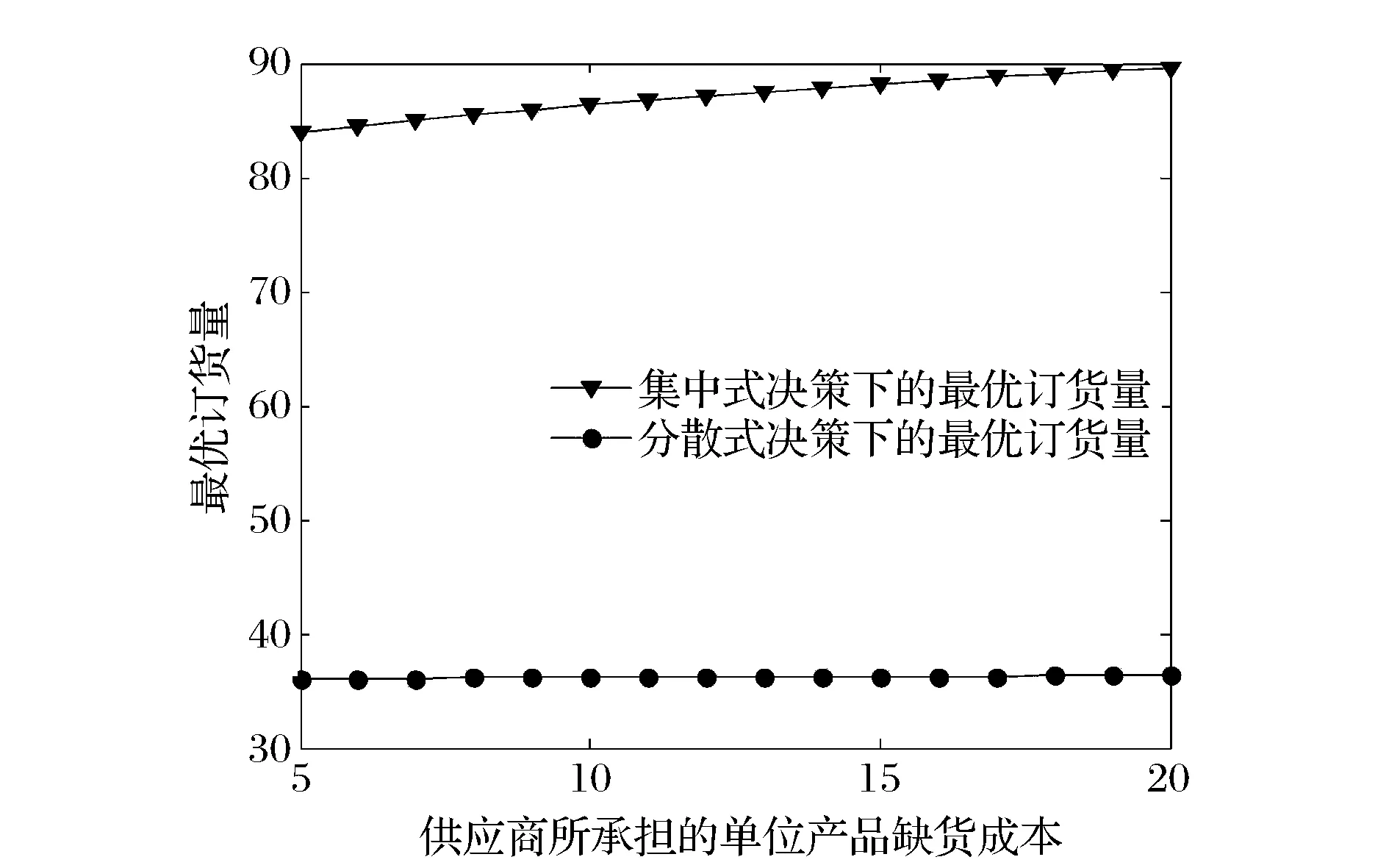
图10 供应商所承担的单位产品缺货成本对最优订货量的影响
6)将单位剩余产品的净残值v视为变量,进行相关的数值实验。考察参数v的变化(如考虑v从0变化到15)对分散和集中式决策下最优产品质量水平与最优订货量的影响,且参数实验分析结果如图11和12所示。由图11和12可知,随着单位剩余产品的净残值的增加,最优产品质量水平在分散式决策下是增加的,在集中式决策下则是减少的且变化相对不敏感,而最优订货量在分散与集中式决策下均是增加的。
7)将损失规避系数λ视为变量,进行相关的数值实验。考察参数λ的变化(如考虑λ从2变化到20)对分散和集中式决策下最优产品质量水平与最优订货量的影响,且参数实验分析结果如图13和14所示。由图13和14可知,随着损失规避系数的增加,最优产品质量水平与最优订货量在分散式决策下均是减少的且变化相对不敏感,而在集中式决策下均是不变的(式(15)不含参数λ)。
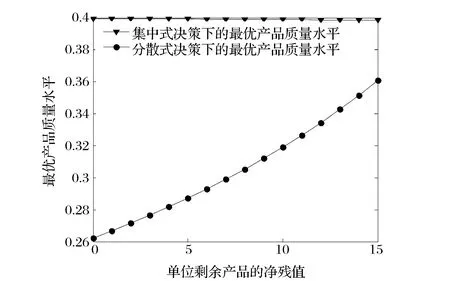
图11 单位剩余产品的净残值对最优产品质量水平的影响
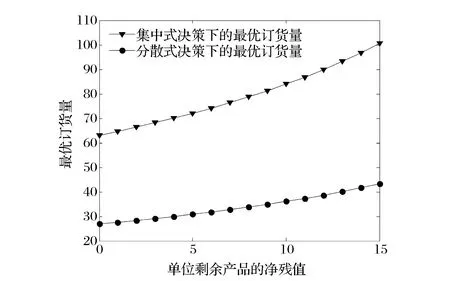
图12 单位剩余产品的净残值对最优订货量的影响
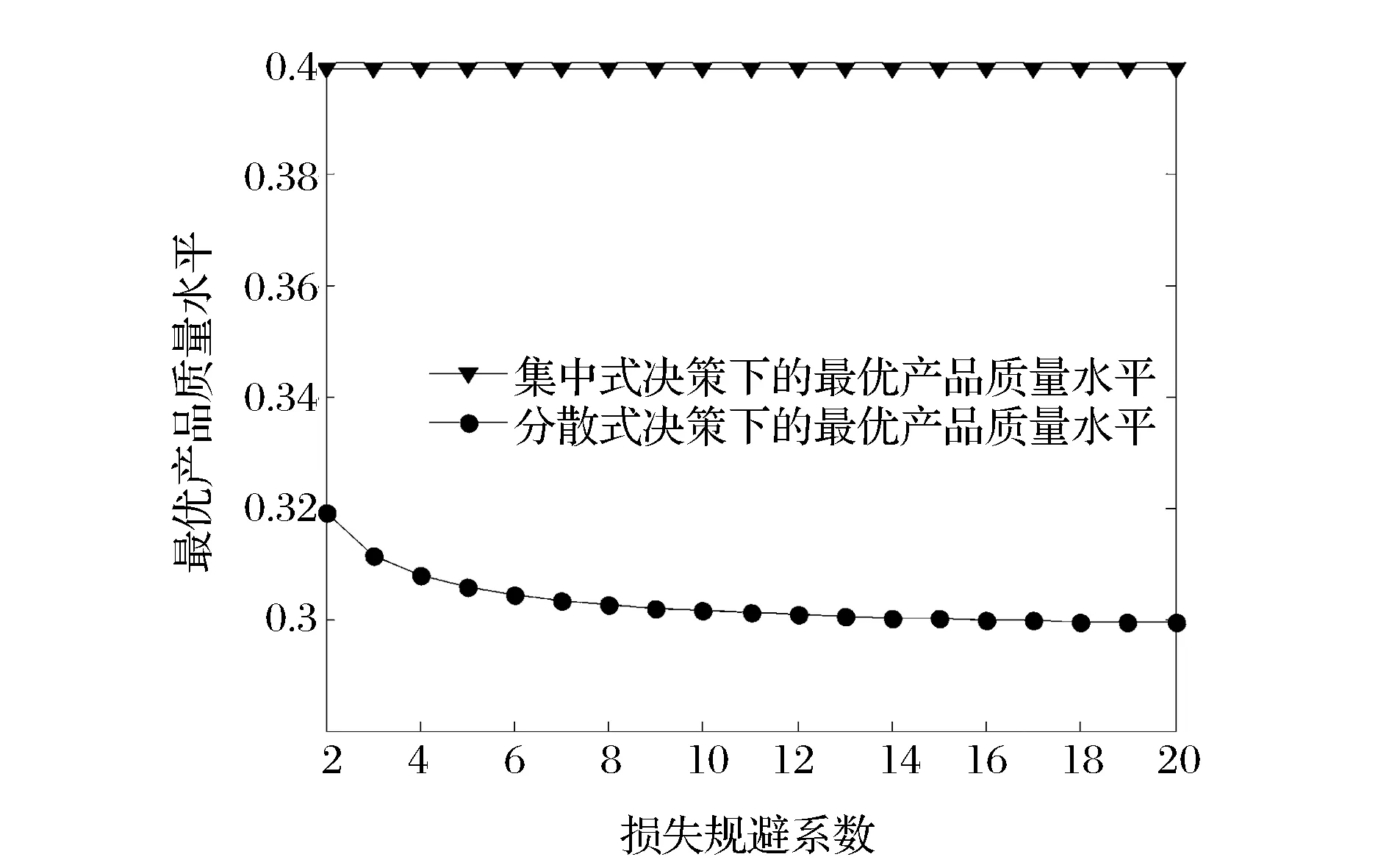
图13 损失规避系数对最优产品质量水平的影响
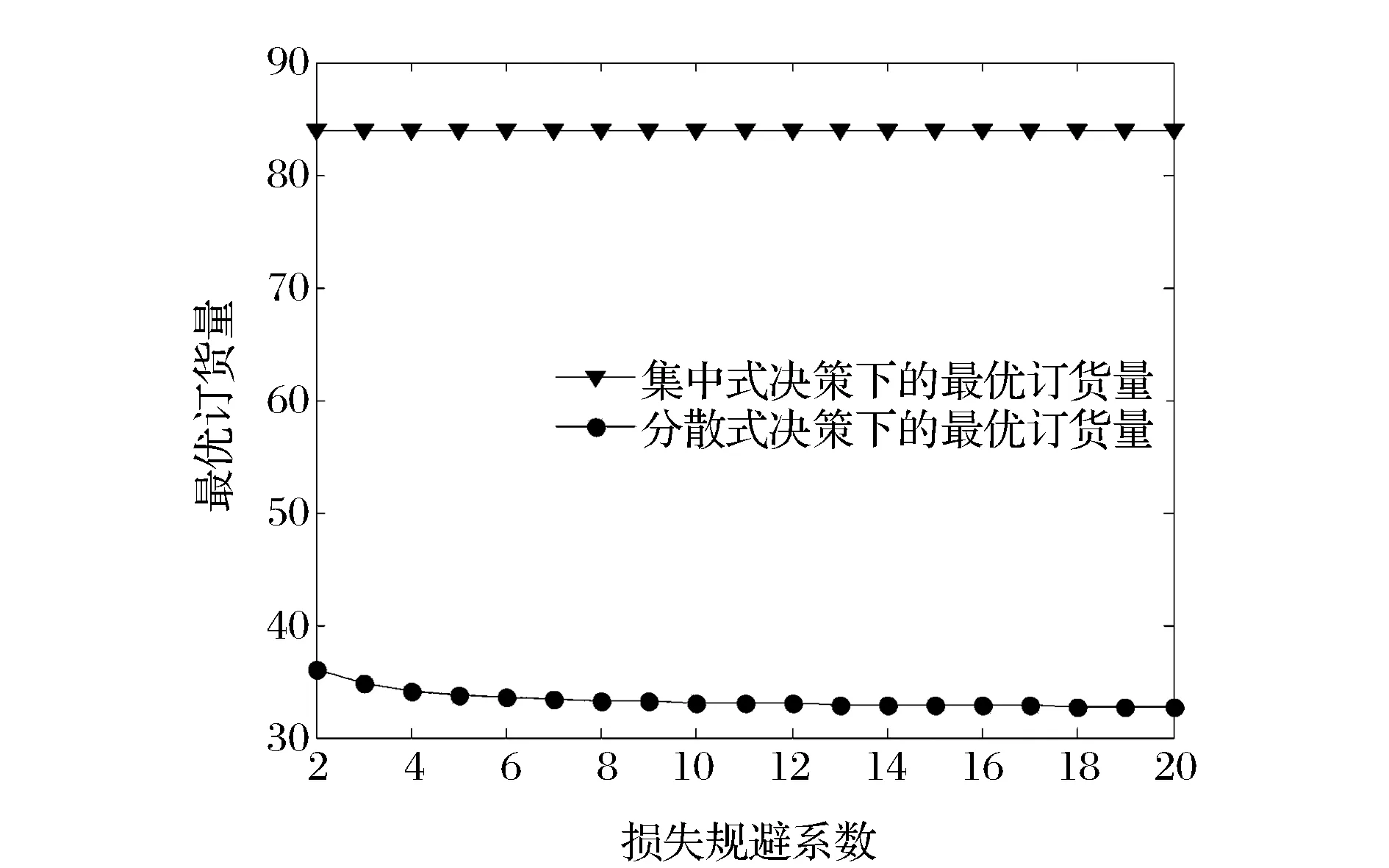
图14 损失规避系数对最优订货量的影响
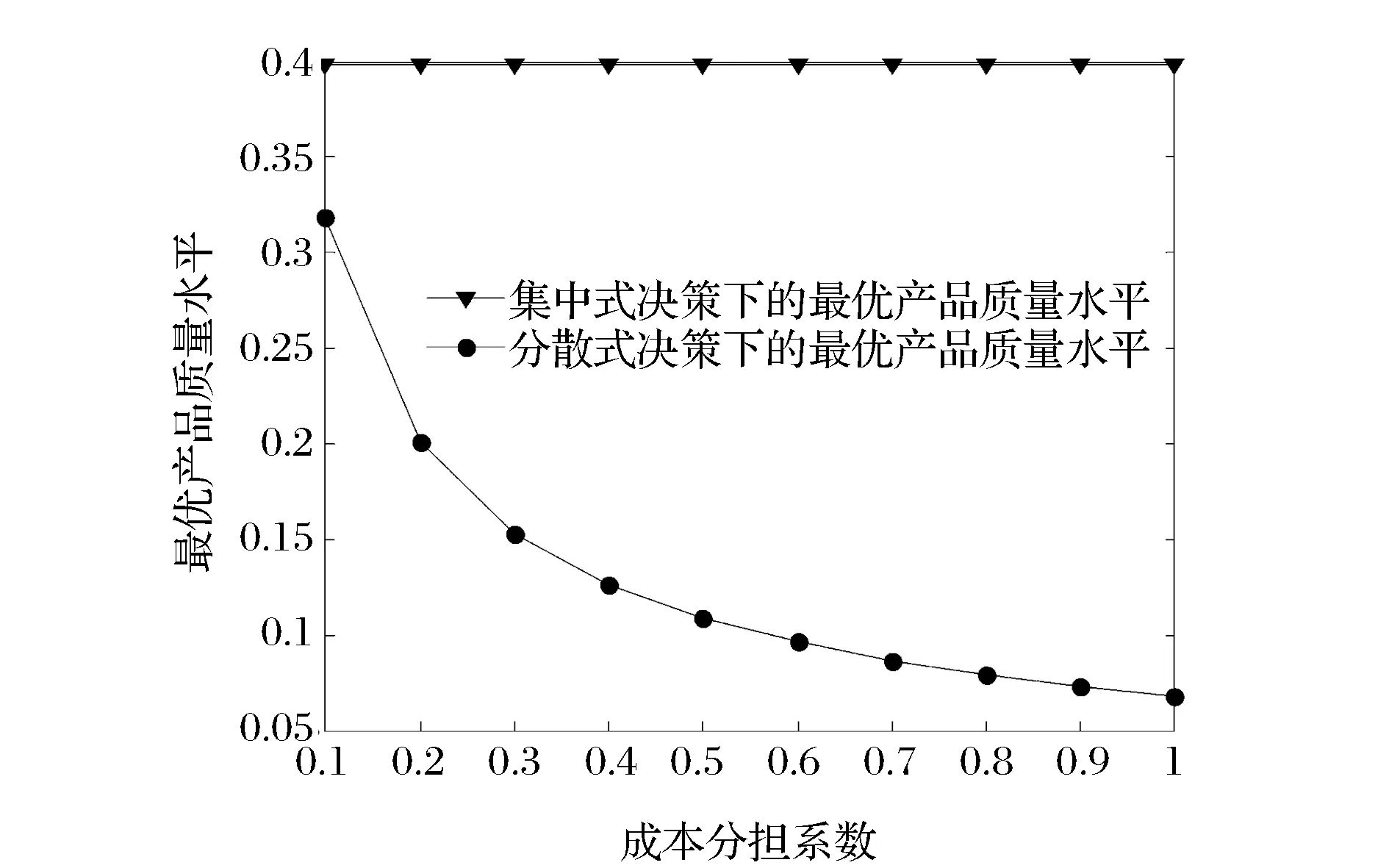
图15 成本分担系数对最优产品质量水平的影响
8)将成本分担系数α视为变量,进行相关的数值实验。考察参数α的变化(如考虑α从0.1变化到1)对分散和集中式决策下最优产品质量水平与最优订货量的影响,且参数实验分析结果如图15和16所示。由图15和16可知,随着成本分担系数的增加,最优产品质量水平与最优订货量在分散式决策下均是减少的且最优订货量的变化相对不敏感,而在集中式决策下均是不变的(式(15)不含参数α)。
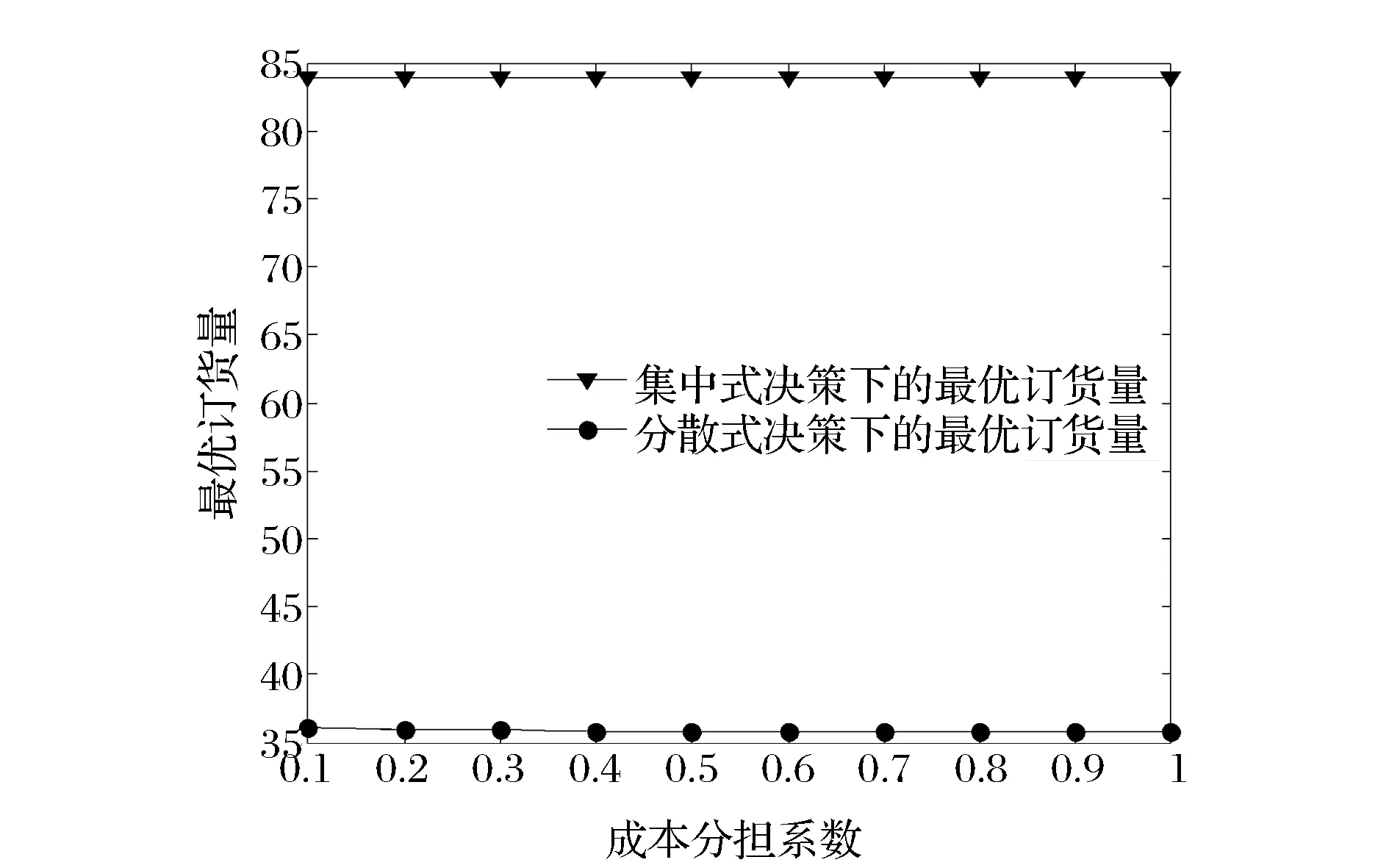
图16 成本分担系数对最优订货量的影响
5 结语
本文在随机市场需求受供应商的产品质量水平影响的前提下,针对由一个风险中性的供应商与一个损失规避型零售商组成的二级供应链协调问题,分别讨论了分散和集中式决策下的最优策略,同时分析了二级供应链在批发价格契约下的协调情况,进一步地构建了批发价格-质量成本分担契约下的供应链协调契约模型,并证明了该供应链协调契约模型的有效性,最后通过数值实验分析了模型参数变动对分散和集中式决策下最优策略的影响。通过本文的研究,得到如下主要结论:1) 在分散式决策下,供应商的产品质量水平为损失规避型零售商的订货量的严格递增函数,损失规避型零售商的订货量为供应商的产品质量水平的严格递增函数;2) 在集中式决策下,供应商的产品质量水平为零售商的订货量的严格递增函数,零售商的订货量为供应商的产品质量水平的严格递增函数;3) 批发价格契约不能协调此二级供应链;4) 一定条件下批发价格-质量成本分担契约能够协调此二级供应链。与已有相关研究不同的是,本文同时考虑了零售商的损失规避行为与市场需求受供应商的产品质量水平影响的情形,得出的研究结论具有实际意义。今后需要进一步开展的研究工作为:考虑损失规避型供应商与促销努力水平的供应链协调契约模型研究;考虑供应链成员具有损失规避行为且市场需求受产品质量水平、促销努力水平等因素影响情形下的供应链协调契约模型研究等。
[1]LariviereMA,PorteusEL.Sellingtothenewsvendor:Ananalysisofprice-onlycontracts[J].Manufacturing&ServiceOperationsManagement, 2001, 3(4): 293-305.
[2]CachonGP,LariviereMA.Supplychaincoordinationwithrevenue-sharingcontracts:Strengthsandlimitations[J].ManagementScience, 2005, 51(1): 30-44.
[3]TaylorTA.Supplychaincoordinationunderchannelrebateswithsalesefforteffects[J].ManagementScience, 2002, 48(8): 992-1007.
[4]KrishnanH,KapuscinskiR,ButzDA.Coordinatingcontractsfordecentralizedsupplychainswithretailerpromotionaleffort[J].ManagementScience, 2004, 50(1): 48-63.
[5]RajuJ,ZhangZJ.Channelcoordinationinthepresenceofadominantretailer[J].MarketingScience, 2005, 24(2): 254-262.
[6]ForkerLB.Factorsaffectingsupplierqualityperformance[J].JournalofOperationsManagement, 1997, 15(4): 243-269.
[7]XieGang,YueWuyi,WangShouyang,etal.Qualityinvestmentandpricedecisioninarisk-aversesupplychain[J].EuropeanJournalofOperationalResearch, 2011, 214(2): 403-410.
[8]GansN.Customerloyaltyandsupplierqualitycompetition[J].ManagementScience, 2002, 48(2): 207-221.
[9]RenZJ,ZhouYongpin.Callcenteroutsourcing:Coordinatingstaffinglevelandservicequality[J].ManagementScience, 2008, 54(2): 369-383.
[10]BaimanS,FischerPE,RajanMV.Information,contracting,andqualitycosts[J].ManagementScience, 2000, 46(6): 776-789.
[11]LinC,ChowWS,MaduCN,etal.Astructuralequationmodelofsupplychainqualitymanagementandorganizationalperformance[J].InternationalJournalofProductionEconomics, 2005, 96(3): 355-365.
[12]FrancaRB,JonesEC,RichardsCN,etal.Multi-objectivestochasticsupplychainmodelingtoevaluatetradeoffsbetweenprofitandquality[J].InternationalJournalofProductionEconomics, 2010, 127(2): 292-299.
[13]RongA,AkkermanR,GrunowM.Anoptimizationapproachformanagingfreshfoodqualitythroughoutthesupplychain[J].InternationalJournalofProductionEconomics, 2011, 131(1): 421-429.
[14] 朱立龙, 于涛, 夏同水. 创新驱动下三级供应链分销渠道产品质量控制策略研究[J]. 系统工程理论与实践, 2014, 34(8): 1986-1997.
[15] 李永飞, 苏秦, 刘强. 合作环境及Shapley讨价还价下的供应链质量双边谈判[J]. 系统管理学报, 2014, 23(2): 159-165.
[16] 陈瑞义, 琚春华, 盛昭瀚, 等. 基于零售商自有品牌供应链质量协同控制研究[J]. 中国管理科学, 2015, 23(8): 63-74.
[17] 陈章跃, 王勇, 刘华明. 考虑顾客策略行为和产品质量的闭环供应链决策模型[J]. 中国管理科学, 2016, 24(3): 109-116.
[18]GurnaniH,ErkocM.Supplycontractsinmanufacturer-retailerinteractionswithmanufacturer-qualityandretailereffort-induceddemand[J].NavalResearchLogistics, 2008, 55(3): 200-217.
[19]MaPeng,WangHaiyan,ShangJ.Contractdesignfortwo-stagesupplychaincoordination:Integratingmanufacturer-qualityandretailer-marketingefforts[J].InternationalJournalofProductionEconomics, 2013, 146(2): 745-755.
[20]LiuWeihua,XieDong,XuXuecai.Qualitysupervisionandcoordinationoflogisticservicesupplychainundermulti-periodconditions[J].InternationalJournalofProductionEconomics, 2013, 142(2): 353-361.
[21] 但斌, 任连春, 张旭梅. 质量影响需求下的二级供应链协调模型研究[J]. 工业工程与管理, 2010, 15(4): 1-4.
[22] 胡军, 张镓, 芮明杰. 线性需求条件下考虑质量控制的供应链协调契约模型[J]. 系统工程理论与实践, 2013, 33(3): 601-609.
[23] 肖迪, 袁敬霞, 包兴. 质量与价格双重竞争情景下的供应链协调策略分析[J]. 中国管理科学, 2013, 21(4): 82-88.
[24]KahnJA.Whyisproductionmorevolatilethansales?Theoryandevidenceonthestockout-avoidancemotiveforinventory-holding[J].TheQuarterlyJournalofEconomics, 1992, 107(2): 481-510.
[25]FisherM,RamanA.Reducingthecostofdemanduncertaintythroughaccurateresponsetoearlysales[J].OperationsResearch, 1996, 44(1): 87-99.
[26]AnupindiR,BassokY.Supplycontractswithquantitycommitmentsandstochasticdemand[M]//QuantitativeModelsforSupplyChainManagement.Boston:KluwerAcademic, 1999: 197-232.
[27]TsayAA,NahmiasS,AgrawalN.Modelingsupplychaincontracts:Areview[M]//TayurS,GaneshanR,MagazineM.Quantitativemodelsforsupplychainmanagement.Boston:KluwerAcademic, 1999: 299-336.
[28]WuSD,RoundyRO,StorerRH,etal.Manufacturinglogisticsresearch:Taxonomyanddirections[R].TechnicalReport,CornellUniversity, 1997.
[29]KahnemanD,TverskyA.Prospecttheory:Ananalysisofdecisionunderrisk[J].Econometrica, 1979, 47(2): 263-291.
[30]ZhangLong,SongShiji,WuCheng.Supplychaincoordinationofloss-aversenewsvendorwithcontract[J].TsinghuaScience&Technology, 2005, 10(2): 133-140.
[31]WangCX,WebsterS.Channelcoordinationforasupplychainwitharisk-neutralmanufacturerandaloss-averseretailer[J].DecisionSciences, 2007, 38(3): 361-389.
[32]ShiKuiran,XiaoTianjun.Coordinationofasupplychainwithaloss-averseretailerundertwotypesofcontracts[J].InternationalJournalofInformationandDecisionSciences, 2008, 1(1): 5-25.
[33]DengXiaoxue,XieJinxing,XiongHuachun.Manufacturer-retailercontractingwithasymmetricinformationonretailer’sdegreeoflossaversion[J].InternationalJournalofProductionEconomics, 2013, 142(2): 372-380.
[34]ChenXu,HaoGang,LiLing.Channelcoordinationwithaloss-averseretailerandoptioncontracts[J].InternationalJournalofProductionEconomics, 2014, 150: 52-57.
[35] 周永务, 肖旦, 李绩才. 损失规避零售商订货量与广告费用的联合决策[J]. 系统工程理论与实践, 2012, 32(8): 1727-1738.
[36] 李绩才, 周永务, 肖旦, 等. 考虑损失厌恶一对多型供应链的收益共享契约[J]. 管理科学学报, 2013, 16(2): 72-82.
[37] 史成东, 闫秀霞, 闫厚强, 等.Loss-averse测度下考虑政府补贴的双第三方回收再制造闭环供应链[J]. 中国管理科学, 2015, 23(7): 152-158.
[38] 顾波军, 张祥. 风险中性供应商与损失规避零售商基于收益共享契约的供应链协调[J]. 系统管理学报, 2016, 25(1): 67-74.
[39] 刘云志, 樊治平. 考虑损失规避与促销行为的VMI供应链协调契约模型[J]. 工业工程与管理, 2016, 21(2): 22-31.
[40]WangCX,WebsterS.Theloss-aversenewsvendorproblem[J].Omega, 2009, 37(1): 93-105.
[41]SchweitzerME,CachonGP.Decisionbiasinthenewsvendorproblemwithaknowndemanddistribution:Experimentalevidence[J].ManagementScience, 2000, 46(3): 404-420.
[42]CachonGP.Supplychaincoordinationwithcontracts[J].HandbooksinOperationsResearchandManagementScience,SupplyChainManagement:Design,CoordinationandOperation, 2003,11: 227-339.
SupplyChainCoordinationContractModelConsideringLossAversionandQualityLevel
LIU Yun-zhi1,2, FAN Zhi-ping2
(1. School of Management Science and Engineering, Nanjing University, Nanjing 210093, China;2. School of Business Administration, Northeastern University, Shenyang 110167, China)
Supply chain coordination and quality level are two crucial facts for supply chain to obtain a competitive advantage. Therefore, it is necessary to explore and analyze the supply chain coordination problem considering the quality level. In this paper, the two-stage supply chain coordination problem considering loss aversion and quality level is investigated. Based on loss-averse retailer assumption, the loss aversion of retailer is portrayed by the loss-averse utility given by Wang and Webster[31]. Then, the optimal strategies of the supplier and the loss-averse retailer are analyzed at the decentralized supply chian respectively. And the optimal strategies of the supplier and the retailer are analyzed at the centralized supply chain respectively. Meanwhile, the two-stage supply chain coordination problem with the wholesale price contract is studied. Further, a supply chain coordination contract model is constructed by combining the wholesale price contract and the quality cost sharing contract, and the validity of the model is proven. Through the analysis, the several conclusions are obtained as follows: under the decentralized supply chain, the supplier’s quality level strictly increases with the loss-averse retailer’s order quantity, and the loss-averse retailer’s order quantity strictly increases with the supplier’s quality level; under the centralized supply chain, the supplier’s quality level strictly increases with the retailer’s order quantity, and the retailer’s order quantity strictly increases with the supplier’s quality level; the wholesale price contract cannot coordinate the two-stage supply chain; the contract combined the wholesale price contract and the quality cost sharing contract can coordinate the two-stage supply chain under certain conditions. Furthermore, under the decentralized and centralized supply chain, the impacts of the changes of the parameters in the model on the optimal quality level and order quantity are presented through the sensitivity analysis of the parameters. The research results provide theoretical guidance for the supply chain managers or members.
supply chain coordination;loss aversion;quality level;contract model
1003-207(2017)01-0065-13
10.16381/j.cnki.issn1003-207x.2017.01.008
2014-06-08;
2016-05-31
国家自然科学基金资助项目(71271051);中央高校基本科研业务经费资助项目(N140607001, N130606001)
樊治平(1961-),男(汉族),江苏镇江人,东北大学工商管理学院,教授,博士生导师,研究方向:运作管理与决策分析等,E-mail:zpfan@mail.neu.edu.cn.
F274; C931
A

