资源约束下的应急预案重构方法研究
石 彪,池 宏,祁明亮,李加莲
(中国科学院科技政策与管理科学研究所,北京 100190)
资源约束下的应急预案重构方法研究
石 彪,池 宏,祁明亮,李加莲
(中国科学院科技政策与管理科学研究所,北京 100190)
在引入预案的网络计划表达的基础上,为应急处置工序加入了所用资源种类、数量以及完成时间的约束,从提升应急管理的处置效率和处置效果出发,研究了多类突发事件并发或次生时,通过在线重构方式生成应急预案资源调度方案的方法。对制定应急预案资源调度方案的步骤、目标和考虑因素做了分析,并针对并行和互斥两类典型的情景组合问题构建了模型,设计了符合应急管理实际情况的启发式算法,通过一个航空公司的应急预案重构的示例对重构方法的应用过程做了阐述。
应急预案;重构;资源约束
1 引言
从应急预案的编制和使用情况来看,目前的大多数预案仍然是通过对特定类型突发事件的应对经验进行总结得出的应急处置工作流程,这为应急管理者提供了基本的决策支持,但由于在生产领域的应急处置中,应急资源存在总量和关联约束的情形非常普遍,而缺乏资源约束的预案在实际操作层将面临许多障碍。此外,由于突发事件发展演变的复杂性和不确定性,当突发事件爆发后,相对突发的、不确定的需求,应急资源在一定时间窗口内的种类和数量也往往是有限和存在关联的,因此,在突发事件爆发初期,需要根据突发事件的特点,及我们所能获取的来自事件本身和资源状态的信息,将已有的多个针对单一事件的预案通过重构的方式生成新的能够满足复杂突发事件处置需求的应急预案,包括对应急资源的调度方案和处置工序的安排。
应急预案领域的研究最初主要集中在对预案类型、结构和组成内容进行研究[1-2],随着项目管理技术和数学优化等方法逐渐被引入,对预案评估问题,以及应急决策中的预案优化选择与快速生成新预案等问题的研究则逐渐成为新热点。于瑛英等[3-4]提出了基于网络计划表达的可操作预案编制方法和预案评估指标体系。Geldermann等[5]采用多指标决策支持系统(RODOS)对核辐射应急预案的实际处置效果进行了评估。刘吉夫等[6]探讨了预案的完备性评估问题。荣莉莉和杨永俊[7]从知识供需匹配的角度提出了一种评价及诊断预案的方法。李永海等[8]提出了一种基于相似历史案例分析的突发事件应急方案生成方法。温志强[9]提出了构建基于应急预案与案例库的“两案三制”突发事件应急决策模式,强调了案例库建设对于应急决策体制建设的重要性。池宏等[10]结合项目管理理论,提出了动态博弈网络技术的概念和模型,将应急处置看做决策者与突发事件间的动态博弈过程,提出了应急预案在应对过程中动态调整的概念模型。姚杰等[11]分析了事件与应对者之间的动态博弈过程,提出了以满足应急资源需求最大化和应急处置期望成本最小化为目标的预案选择思路。祁明亮等[12]研究了不确定情况下的未来调整的期望成本最小化的预案优化选择问题。在快速生成新预案的问题上,Bryson等[13]建立了0-1规划模型,在满足资源约束条件下,以最大化消除灾害影响为目标,对形成灾害恢复预案(DRP)中的子预案进行选择,但其生成的预案仅是子预案的集合,并没有涉及子预案之间的逻辑关系问题。王庆全等[14]从范畴论的关系复合约束角度,将现有的文本型应急预案转换为由概念及其之间的关系定义的语义信息,从而便于提取相关信息为新的应急情境提供决策辅助,实现了在现有指导性预案基础上快速形成新预案的功能。应急操作预案与指导性预案同属于应急预案范畴,其主要内容可以表示为应急处置动作按照逻辑关系有序组合的工作流程。祁明亮等[15]基于网络计划建立了可操作预案编制方法,根据此方法编制的操作预案包含了事件自身发展的逻辑关系与处置工作之间的逻辑关系,同时为预案的非文本化表达提供了一种可行的思路。刘磊等[16]在将预案表达为网络计划图的基础上,建立了将已有预案分解为多个功能独立的模块,然后根据突发事件发展阶段的应急需求,按照功能与需求匹配的原则重新将模块搭接,从而形成新预案的思路,而未能给出模块如何重新组合的具体算法。
在线重构的概念起源于软件设计领域,是通过调整设计模式或架构来实现软件功能的动态切换,从而提升软件的可扩展性和维护性[17],Estrin在1963年提出了可重构计算的初步设想[18],Xilinx公司在 2001 年发布了一种系统设计理念,即在线可重构技术(Internet Reconfigurable Logic),其核心是通过互联网对远程系统的硬件和软件进行远程更新升级。重构的概念后来被越来越广泛的应用到了制造业和组织设计领域,如可重构制造系统和业务流程重组等。在应急管理领域,近年已有将在线重构的思想应用于应急预案管理的研究[16,19],但主要集中在预案的模块化或形式化表达方面,在通过在线重构方式快速生成应急预案方面仍有很多难点有待解决。
资源约束下的项目调度问题(Resource Constraint Project Scheduling Problem,RCPSP)的研究已经有50多年的历史,是运筹学及运营管理中的重要研究方向,其应用领域涉及交通、建筑、工业生产、软件开发、机场与铁路调度、物流等,近年来,有学者开始将RCPSP模型应用于应急救援领域[20],成为RCPSP应用的一个新领域。
经典的RCPSP是考虑序关系约束、多种资源的总量限制,以最小化项目工期为目标的项目计划问题。随着应用领域的拓展,RCPSP问题的研究从最开始的经典模型发展扩充了许多新问题,包括时间/成本均衡问题[21,22]、时间/资源均衡问题[23]、多模式项目计划问题[24]。另外RCPSP是强NP难问题,对解决RCPSP问题的精确算法和近似算法也出现了大量研究,基于优先级规则的启发式算法较有代表性,其是运用一种或两种调度生成机制[25],并在选择工序时按照一定的优先级选择工序,最后生成一个可行的调度方案的算法。调度生成机制是通过逐步扩展局部进度计划来生成一个完整的可行调度计划,包括以工序为阶段变量的串行调度机制和以时间为阶段变量的并行调度机制;优先规则是在生成调度时给每个工序赋予一个优先值,决定了该工序被选择的顺序和安排的时间,按照计算优先值的对象可以分为网络、时间、资源规则等。
本文将在上述研究基础上,将多个针对单一突发事件的应急预案表达为利于计算机识别和计算的形式,在经典RCPSP问题基础上,增加工序的工期关联约束,将优化目标设定为工期和成本均衡的多目标问题,从提升应急管理的处置效率和处置效果出发,针对预案重构中涉及的两类典型问题,构建基于资源限制的预案重构资源调度模型,为提升应急管理者的应急处置水平提供决策支持。
2 问题描述
在编制应急处置流程方面,动态博弈网络技术是一种讨论较为深入的方法,其认为应急管理在某个时刻后的后续任务是随着前一阶段子任务的完成效果和所处环境的变化而变化的,而应急处置是突发事件的管理者应对阶段性处置结果和突发事件发展趋势的一个动态博弈过程[16]。本文的预案重构思想正是基于此展开的。
2.1 在线重构的思路
应急预案是针对突发事件的所有可能情形,依据应急管理者的历史经验和合理推理得出的应对方案,其中包括具体措施的工作流程和总体的应急资源调度方案。资源调度方案取决于突发事件发生时的资源状态和实际应急需求,具有非常强的动态调整特征,脱离突发事件现场实际情况的预案资源调度方案将缺乏实战价值,这就要求应急预案相关的资源调度方案需要具备实时生成、动态调整的功能。在通过计算机在线重构形式生成预案时,需要根据突发事件实时的应急需求和资源状态来制定相应的资源调度方案,思路见图1。
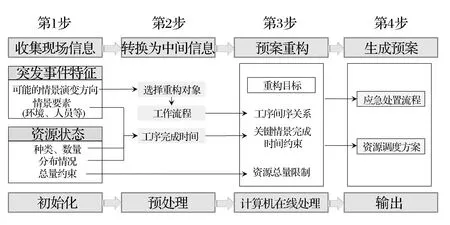
图1 应急预案在线重构的思路
(1)收集现场信息
突发事件爆发初期,首先要收集该事件的特征信息以及相关的资源状态信息。突发事件本身的特征是影响应急救援的关键因素,初期需要收集的突发事件特征信息包括:突发事件可能的场景演变方向、涉及事件发生时间、地点、环境、人员、物资等情况的实时信息、应急处置的特殊需求等;突发事件发生后的可用救援资源是保障应急响应效率的重要因素,初期需要收集的资源状态信息包括:所需应急资源的种类、数量、分布情况和总量约束情况。
(2)转换为中间信息
在第一步收集了突发事件本身特征的基础上,根据分析突发事件可能的场景演变方向,选出需要参与重构的并发或次生突发事件应急预案作为重构对象,并根据突发事件的实时发生时间顺序,对应急处置的工作流程做初步梳理,为下一步计算机在线重构提供工序间的基本序关系信息;此外,还需要根据事件的场景要素以及部分工序调用资源的实时分布情况,对工序的完成时间估计做出调整。
(3)在线重构
预案重构的资源调度问题是在以上两步给出基本工作流程以及工序完成时间估计的基础上,以最大化应急处置效率以及最小化突发事件造成的损失为目标,将工序间基本序关系、关键场景点的最晚完成时间和资源总量限制作为最终约束的优化问题,通过计算机在线处理的方式实现预案资源的最优化配置。
(4)生成预案
作为预案重构的结果,计算机将在线输出满足工序间逻辑关系约束和资源总量约束的应急预案,这包括每个工序执行顺序的应急处置流程和经过优化的实时资源调度方案。
2.2 在线重构的目标
从提升突发事件应急管理水平的角度来看,应急处置的效率和效果是应急管理者最为关注的两个方面,预案重构的建模也将从最大化应急处置效率和最小化突发事件的损失两个维度构造目标函数。
(1)最大化应急处置效率
突发事件对公共秩序、人身财产安全等方面造成的危害常常因为其突然爆发和持续时间过长而被不断放大,因此,突发事件应急处置的基本目标都是为了尽快控制突发事件造成的危害,使一切尽快恢复常态。衡量突发事件应急处置的效率需要重点关注以应急处置持续时间为代表的时间效率。按照应急处置的阶段划分,应急处置被划分为资源准备阶段、应急处置阶段和应急善后阶段,从每个阶段的处置目标来看,由于突发事件爆发突然,要求应急处置尽快开始,因此资源准备阶段的处置目标需要以处置时间最小化为首要目标,其次才是考虑资源准备带来的额外成本因素;在应急处置和善后阶段,由于应急救援已经开始,这时考虑的处置目标应以最大化处置效果为主要目标,而以处置持续时间为代表的处置效率将作为次要目标,但是,考虑到突发事件的基本目标是使事件尽快得到控制,因此,在应急处置和善后阶段的处置效果又与处置效率密切相关,本文以下将不再区分不同阶段的应急处置目标区别,以最大化应急处置效率,即最小化各阶段总体应急处置持续时间为首要目标。
(2)最小化突发事件造成的损失
突发事件造成的直接损失大小受突发事件类型、规模、发生时间、地点的影响,受应急处置的影响非常小,但在突发事件应急处置过程中可能的一些间接损失却是可以控制的。比如资源准备阶段调运特定种类的物资,如果不加规划,往往是有多少调运多少,当突发事件的危害低于预期时势必造成物资闲置的额外损失,当突发事件的危害高于预期时又会造成物资准备不足带来的更大规模的额外损失。因此,从应急管理的角度最小化突发事件造成的间接损失,尽可能降低由于资源调运和使用带来的额外损失,将成为制定预案资源调度方案需要考虑的另一个目标。
2.3 在线重构的关键问题
编制应急预案需要考虑突发事件发生发展过程中各种可能出现的情景,本文将情景界定为突发事件演变场景的集合,而场景是指由处置主体要素、影响处置的周边环境要素以及设备等资源要素共同构成的随时间不断变化的一系列要素状态取值的集合。由于突发事件的应急处置过程具有明显的阶段性特征,当突发事件性质发生变化、处置空间或对象发生改变、处置任务目标发生变动时,都会伴随着场景的某些关键状态取值发生变化,对应着同一预案中可能包含有多个可能发生的情景,这些情景之间存在并行和互斥两种关系,并行是指多个情景可以同时并行发生,如停水和停电两种情景;互斥是指多个情景在实际情形中只有一种能够发生,如发生火情和未发生火情两种情景。
在存在资源约束的预案重构问题中,这两类问题的处理除了需要考虑工序之间的序关系,还需要考虑工序之间的并行或互斥关系对资源调度的影响,以下将从资源约束的角度对这两类典型的重构问题分别加以研究。
(1)并行情景之间的组合问题
在对并发或次生情形下的多个预案进行重构时,每个预案中都可能存在多个情景,将每个预案中的情景与其他预案的情景进行组合之后,才能形成多类突发事件并发或次生时的各种可能情景,这种组合问题是在最优化处置效率和处置成本的目标下,为多个并行的工序安排资源调度方案。问题可以描述为:已知应急预案中工序持续时间和调用资源数量的关系;工序间的基本序关系;资源总量限制的时间窗口;关键场景点的完成时间约束等。在最小化应急处置持续时间和资源调用的成本的目标下,确定各个工序的结束时间和资源调用量。考虑约束如下:
1)资源与工期的关联性约束。应急响应分为应急准备和处置、善后三个阶段,由于准备阶段的工序工期主要取决于资源调运的运输时间,而处置和善后阶段工序的工期主要取决于资源的使用时间。因此,假设准备阶段的工期与调运资源的数量呈正相关,而处置和善后阶段的工期与使用资源的数量呈负相关。
2)工序间资源的关联性约束。部分准备阶段的工序准备的资源是供后续处置和善后阶段工序使用的,其资源量之间存在关联。
3)资源总量的约束。应急处置对资源的需求往往是针对人员、物资或设备而言的,这些都属于可再生资源范畴,其数量会得到不断补充,但调用总量受储备水平和调用时间等影响,在某个时刻会有上限约束,这些存在上限约束的时刻集合就是该资源的总量限制时间窗口。如航空公司突发事件预案中对运行控制人员的调用受值班人数和抽调时间的约束,在突发事件刚发生的一段时间内会存在人数调用上限。
4)工序间的序关系约束。每个情景都有定义部分工序的序关系,当多个并行情景合并时,部分工序之间的序关系约束可能会出现矛盾(短路,环路,断路),需要根据实际情况进行修正后形成组合情景中工序之间的基本序关系。
5)工序的唯一性约束。工序的唯一性是指任何工序在同一情景中只能被执行一次。在进行组合的多个并行情景中,都包含有大量的工序,大部分工序具有不同的名称和工期参数,其在执行过程中只用执行一次,但也有部分工序是多个情景的公共工序,在将多个并行情景组合为一个情景时,当某个公共工序在组合情景中的执行时间存在重叠或搭接关系时,可以合并为一次执行;而当其在组合情景中的执行时间不存在重叠或搭接关系时(如某个预案必须在中途启动时,部分公共工序则可能必须重新执行),则需要将该公共工序标记为不同的工序,在组合后生成的情景中执行多次。
6)关键场景点的完成时间约束。在并发的多个情景进行组合时,需要根据突发事件应急处置的具体需求,为部分关键情景点的完成时间设置最迟完成时间。
(2)互斥情景之间的组合问题
由并行情景之间组合得出的只是多类突发事件并发或次生情形下的可能情景,需要将这些相对独立的情景进行再次组合,最终形成包含所有可能情景的整体应急预案。由于并行情景之间组合得到的情景中可能包含单个预案中的多个互斥情景,因此,这些情景之间的再次组合可能涉及多个互斥情景之间的组合问题,其与并行情景之间的组合问题的不同之处在于对资源准备阶段的公共工序进行资源调度时需要综合考虑后续互斥工序的资源需求,由于多个互斥分支工序之间只有一种能够实际发生,其资源需求具有不确定性,因此组合情景中公共工序的资源调度方案应综合考虑所有可能情景出现时对方案进行调整的灵活性。当公共工序的资源准备数量不足时,会产生额外的资源补充成本(紧缺成本);当资源准备过剩时,会产生额外的闲置成本。公共工序的鲁棒资源调用量可以描述为在期望额外成本最小(紧缺成本+闲置成本)目标下的资源调用量,在组合后的情景中按照这一方案实施,将使得当任何一种互斥情景实际发生时,资源准备的数量与实际需求的偏差都不会过大。该组合问题可以描述为如下问题:已知应急预案中工序持续时间和调用资源数量的关系;互斥情景的发生概率;工序间的基本序关系;资源总量限制的时间窗口;关键场景点的完成时间约束等。在最小化应急处置持续时间和资源调用成本的目标下,确定各个工序的结束时间和资源调用量。
3 模型构建
3.1 变量定义
S:情景集合,s∈S;
Ia:应急准备阶段工序集合;
Ib:应急处置阶段工序集合;
Ic:应急善后阶段工序集合;
I:工序集合,i,j∈I={1,2,…n},n代表所有工序中的末尾工序,I=Ia+Ib+Ic;
EFi:工序i的最早完成时间;
LFi:工序i的最晚完成时间;
K:资源种类集合,k∈K={1,2,3,4}={人员、工具、设备、物资};
Q:序关系集合,(i,j)∈Q;
Θ:关键工序集合,θ∈Θ;
B(θ):能够确定关键工序θ时间的工序集合,B(θ)⊆I;
tθ:关键工序θ的目标时间;
xsit:0-1变量,如果情景s中的工序i在时刻t完成则为1,否则为0;
rsik:情景s中工序i调用资源k的数量;
Nsik:情景s中工序i对资源k的需求量;
psi:情景s中工序i的工期;
psi_:表示情景s中工序i的工期下限;
psi-:表示情景s中工序i的工期上限。
准备阶段工序的工期主要取决于资源调集的时间。对于所需资源储备数量较少,需要多次调运的,其工期取决于需要调配资源的数量,如果存在多种资源需要调集时,其工期取决于关键资源的需求数量;对于所需资源储备数量充足,可以采取一次或并行调集的,其工期受资源量的影响不大。假设以上两种模式的工序具有如下关系:
usi:表示准备单位关键资源k*所用的工期,usi≥0:vsi为常数;
处置和善后阶段的工序都是在既定资源准备基础上完成的工作。有些工序的工期主要取决于所用关键资源数量的大小,所能调用的资源越多,其工期越短。比如处置阶段的客货安置,地服人员越多,其安置所需时间越短;但也有部分工序的工期与所用资源量的多少无关,如残损航空器搬移,并非拖车越多越快,其处置时间基本不受拖车数量的影响。假设以上两种工序的工期有如下关系:
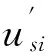
vsi为常数;
Tk:资源k被有总量约束的时间段集合;
Rkt:资源k在时刻t内的总量约束;
ck:单位资源k在准备阶段的准备成本;
gk:单位资源k在处置阶段的调用成本;
ηs:情景s的发生概率;
Φk:资源k的单位临时调用成本(紧缺成本);
Γk:资源k的单位闲置成本;
3.2 并行的多个情景之间的组合问题
(1)
(2)
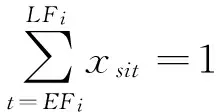
(3)
(4)
psi_≤psi≤psi-
(5)
(6)
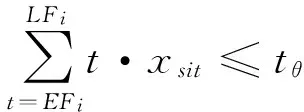
(7)
xsik∈{0,1}
(8)
(1)表示最小化应急处置的持续时间;(2)表示资源准备和调用的总成本最小;(3)表示工序的唯一性约束;(4)表示工序之间的序关系约束;(5)表示工序的工期上下限约束;(6)表示资源总量限制窗口内的资源总量限制;(7)表示关键场景的完成时间约束。
3.3 互斥的多个情景之间的组合问题
(1)公共工序的最优决策问题
(9)
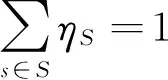
(10)
Nsik≥0;Φk≥0;Γk≥0;rsik≥0
(11)
(9)表示最小化各种互斥情景发生时,由于资源紧缺或闲置造成的期望损失;(10)表示情景集合S包含了所有可能发生的情景。
(2)公共工序确定情形下的后续工序安排问题
针对每个情景分支,计算后续工序最优开工时间和资源调用量,情景分支后的工序之间互不影响。只需要在并行情景组合优化模型的基础上增加公共工序的执行约束即可。
4 算法设计
4.1 并行情景组合问题求解
此问题为多目标0-1整数规划问题,目标1是最小化预案总的执行时间,目标2是最小化应急处置成本。从应急管理的实际背景考虑,应对突发事件的时间要求更为迫切,而资源调用产生的成本只要在可接受的范围内就可以了。应急处置和善后阶段使用的资源有的是在应急准备阶段准备的,其资源的准备和使用数量之间存在关联,资源量的增加会导致准备阶段工序的工期增加,而处置和善后阶段的工序工期则会相应减少(见图2)。因此,从目标1来看,需要对处在关键路径上的这部分工序进行资源量的最优配置;从目标2来看,需要尽可能减少工序对资源的调用数量,但这必须是在保证目标1实现的前提下实现的。以下设计的启发式规则是以最小化预案总的执行时间为首要目标,在此基础上考虑是否可以尽可能减少资源准备和使用产生的成本。
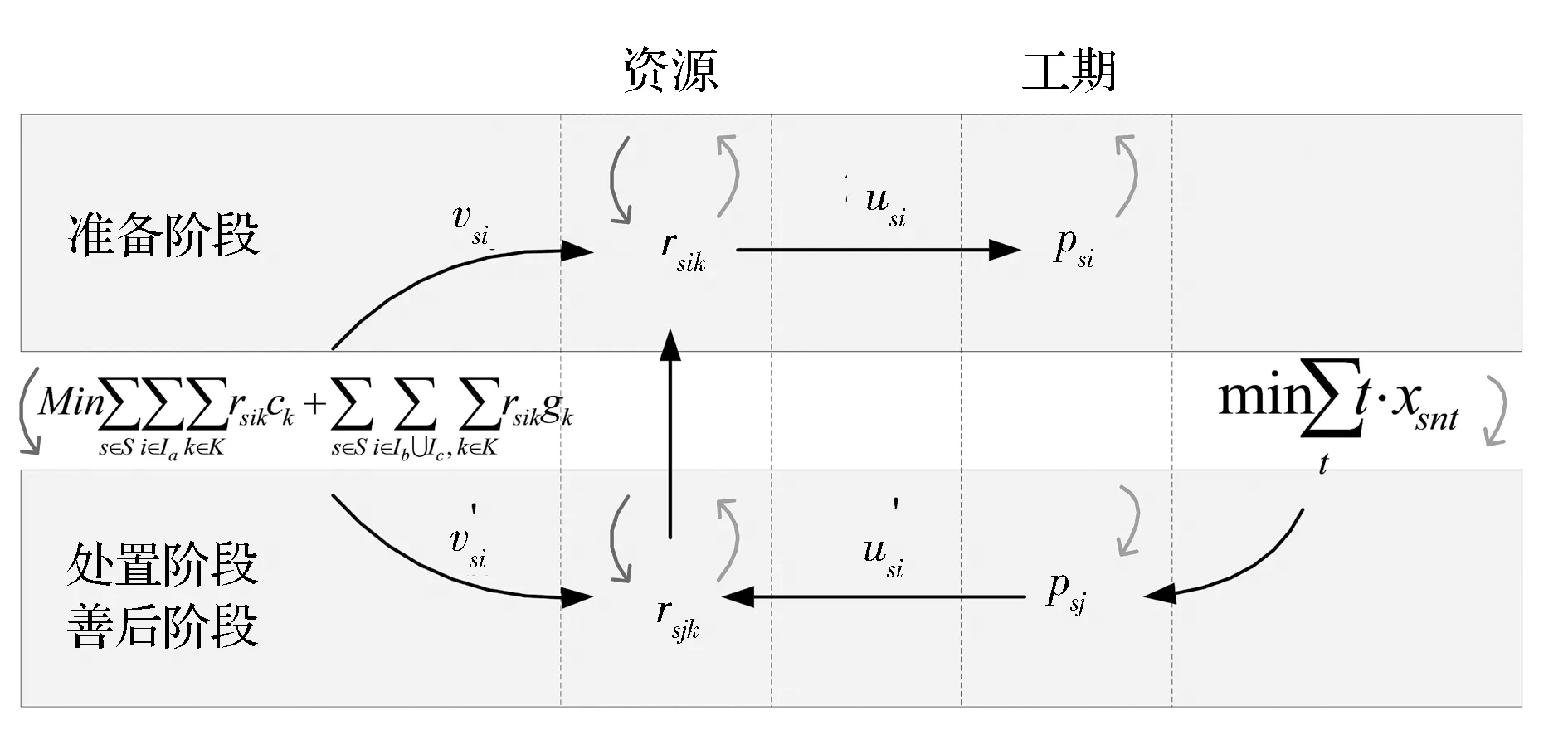
图2 并行情景组合问题的数学模型
预案中的工序按照其工期之间的影响关系可以分为三类:
Ⅰ类工序集:在准备阶段和处置善后阶段都涉及同种资源调用的工序,其处置善后阶段使用的资源需要在准备阶段提前准备,这部分工序的资源准备量和资源使用量相等,当处于不同阶段的这些工序的工期都与资源量有关时,这些工序组成的工序集合被定义为I类工序集,当这些工序处在预案的关键路径上时,需要综合考虑同一资源量调整时对多个工序工期造成的影响;
Ⅱ类工序集:同样针对在准备阶段和处置善后阶段都涉及同种资源调用的工序,当处于某个阶段或两个阶段的工序工期都与资源量无关时,这些工序组成的集合被定义为Ⅱ类工序集,当这些工序处在预案的关键路径上时,只需要考虑压缩工期与资源量有关的那些工序的工期即可;
Ⅲ类工序集:除了Ⅰ类和Ⅱ类工序集之外,预案还有一些工序是仅在准备阶段或处置(善后)阶段单独出现调用某种资源,这些工序的工期之间相互独立,其组成的集合定义为Ⅲ类工序集,当这类工序处在预案的关键路径上时,只需将其尽量压缩至工期下限即可。
启发式规则如下:
1)在满足序关系和资源总量约束的前提下,优先安排有目标完成时间限制的关键工序,以保障处置善后阶段的资源需求为主,生成初始调度方案;
2)针对Ⅰ、Ⅱ、Ⅲ类工序集分别设计调度算法,压缩关键路径工期;
3)针对非关键路径上的工序,压缩其资源调用数量,以最小化资源调用成本。
算法具体步骤:
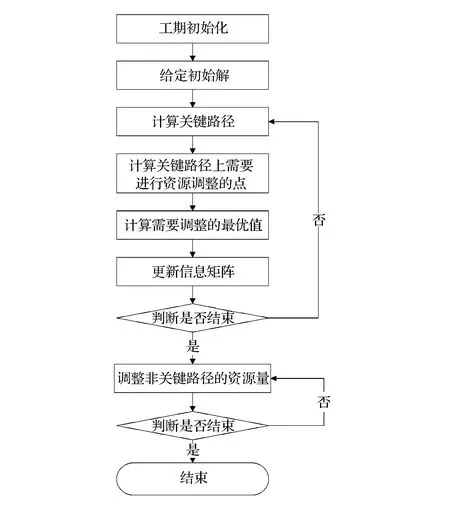
图3 并行情景组合问题的算法流程图
步骤1:按照优先安排关键工序和保障处置和善后阶段的资源需求规则进行工期初始化。
构造Ⅰ类工序集
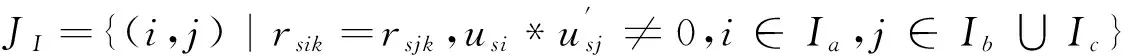
psj=psj-,psi=usi·rsjk+vsi;
构造II类工序集
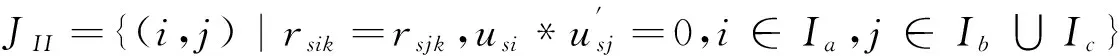
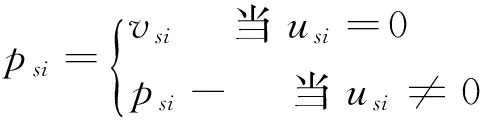
构造III类工序集JIII=I-JI-JII,令
步骤2:生成初始解。
采用串行调度生成机制,一共进行g=1,…,n次迭代,每次迭代选取一个工序g,计算其前序工序集合中所有工序的最晚开始时间,每次选择最晚开始时间最早的工序进行安排。选定工序后,按照初始化工期生成该工序调度方案,g=g+1,直至所有工序安排完毕;
步骤3:压缩关键路径工期。
计算初始关键路径CP0的总工期P0,构建关键路径集合CP={CPn|Pn=min{P0,…Pn}},t=0;
步骤3.1:将关键路径上的工序区分I,II,III类形成集合JI,JII,JIII,针对JI,JII,JIII中的工序,分别执行 步骤3.2~3.4;
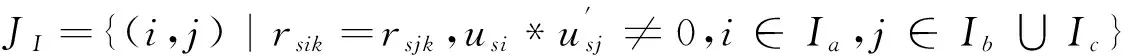
步骤3.2.1:判断如果使用同种资源的m个工序{jm}之间存在序关系,则令
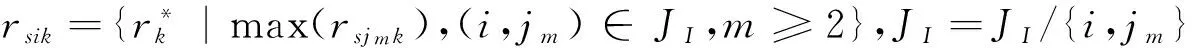
步骤3.2.2:令
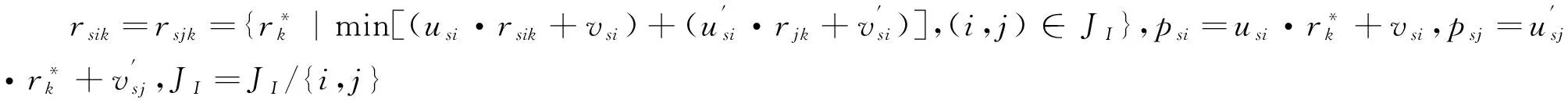
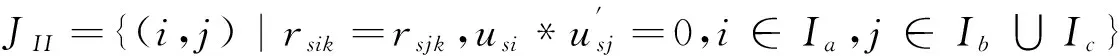
步骤3.3.1:令rsik=rsik-1,JII=JII/{i,j},转步骤3.3;
步骤3.3.2:令rsjk=rsjk+1,JII=JII/{i,j},转步骤3.3;
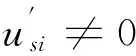
步骤3.4.1:令rsik=rsik-1,JIII=JIII/{i,j},转步骤3.4;
步骤3.4.2:令rsik=rsik+1,JIII=JIII/{i,j},转步骤3.4;
步骤3.4.3:令JIII=JIII/{i,j},转步骤3.4;
步骤3.5:计算关键路径CPt的总工期Pt,判断:如果CPt和CPt-1完全相同,则转步骤4.1;如果CPt和CPt-1存在不同工序,且Pt=Pt-1,则转步骤4.2;其他,转步骤3.1;
步骤4:压缩非关键路径上的资源量。
步骤4.1:在不改变CPt的前提下,减少非关键路径上的资源量;
步骤4.2:在不改变CPt或CPt-1的前提下,分别减少非关键路径上的资源量,根据资源总调用成本最小,确定关键路径及资源用量。
4.2 互斥情景组合问题求解
问题分解为情景分支之前的公共工序决策问题,和公共工序确定情形下的各分支后续工序安排问题,前者可以通过求解单目标的优化模型求解;后者可以通过增加公共工序工期和完成时间约束,结合并行情景组合模型求解。
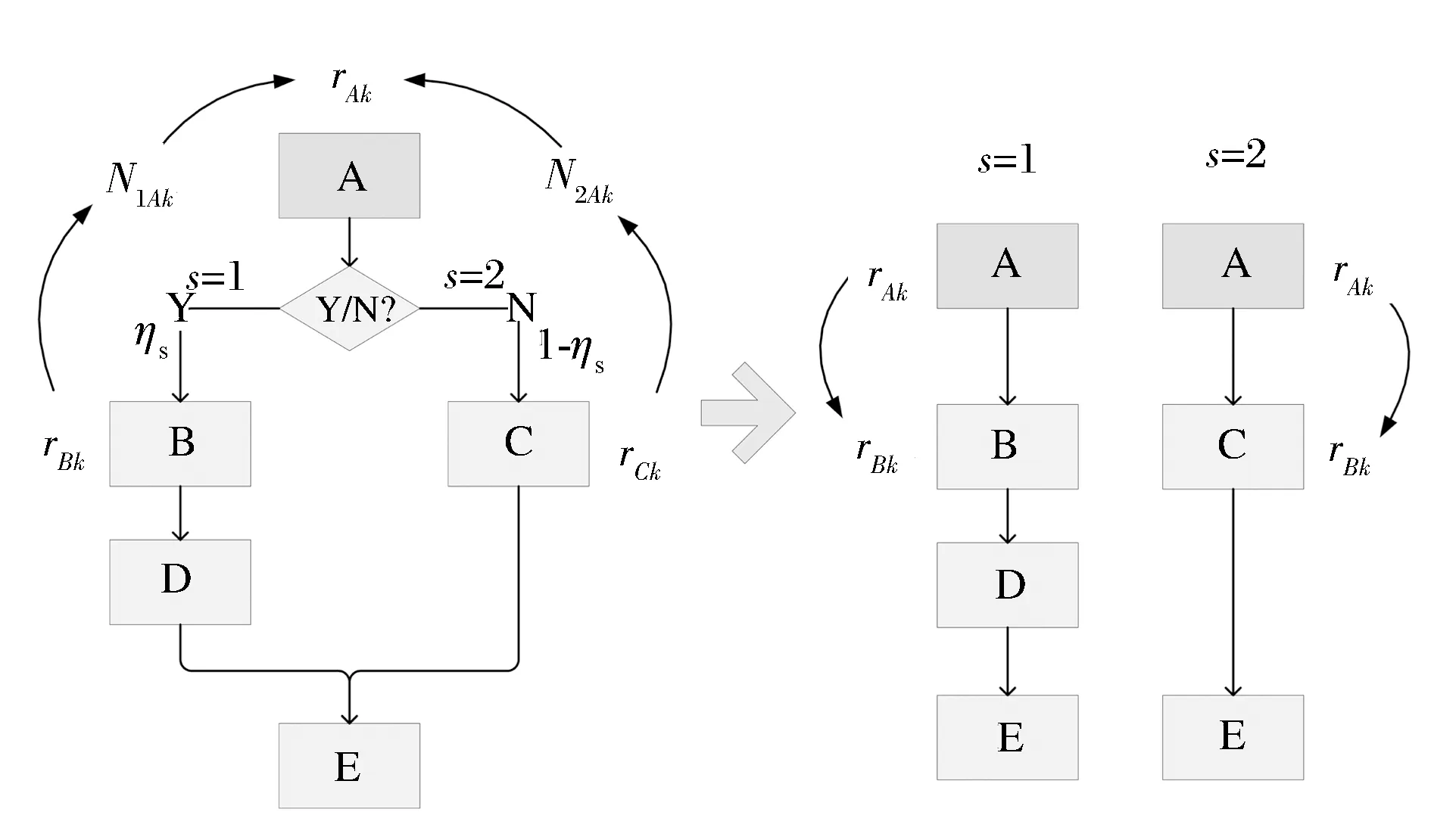
图4 互斥情景组合问题的数学模型
5 算例分析
5.1 案例场景假设
(1)在t=0时刻,AOC接到某航班飞机空中颠簸信息后,启动空中颠簸应急预案;
(2)在t=30时刻,AOC接到该航班起落架故障信息,随即启动起落架故障应急预案;
(3)飞机燃油将在85分钟后耗尽,在此时刻将执行紧急迫降;
(4)由于航班信息收集、航班运行监控和运控支持都需要运控中心的临时人员支持,其在接受任务后30分钟内的人员调用总量上限为6人;
(5)飞机载有乘客和机组共200人。
5.2 预案及工序参数
航空公司空中颠簸和起落架故障应急预案的处置流程图见图5、图6,工序参数见附表1和附表2。
5.3 并行情景之间的组合
以Sij表示事件i中的情景j;以Gi表示情景组合i;以G表示情景组合构成的集合。此处i=1表示空中颠簸,i=2表示起落架故障;G1=S11+S21为例,执行如下处理:
(1)合并为一次执行的工序(见表1)。
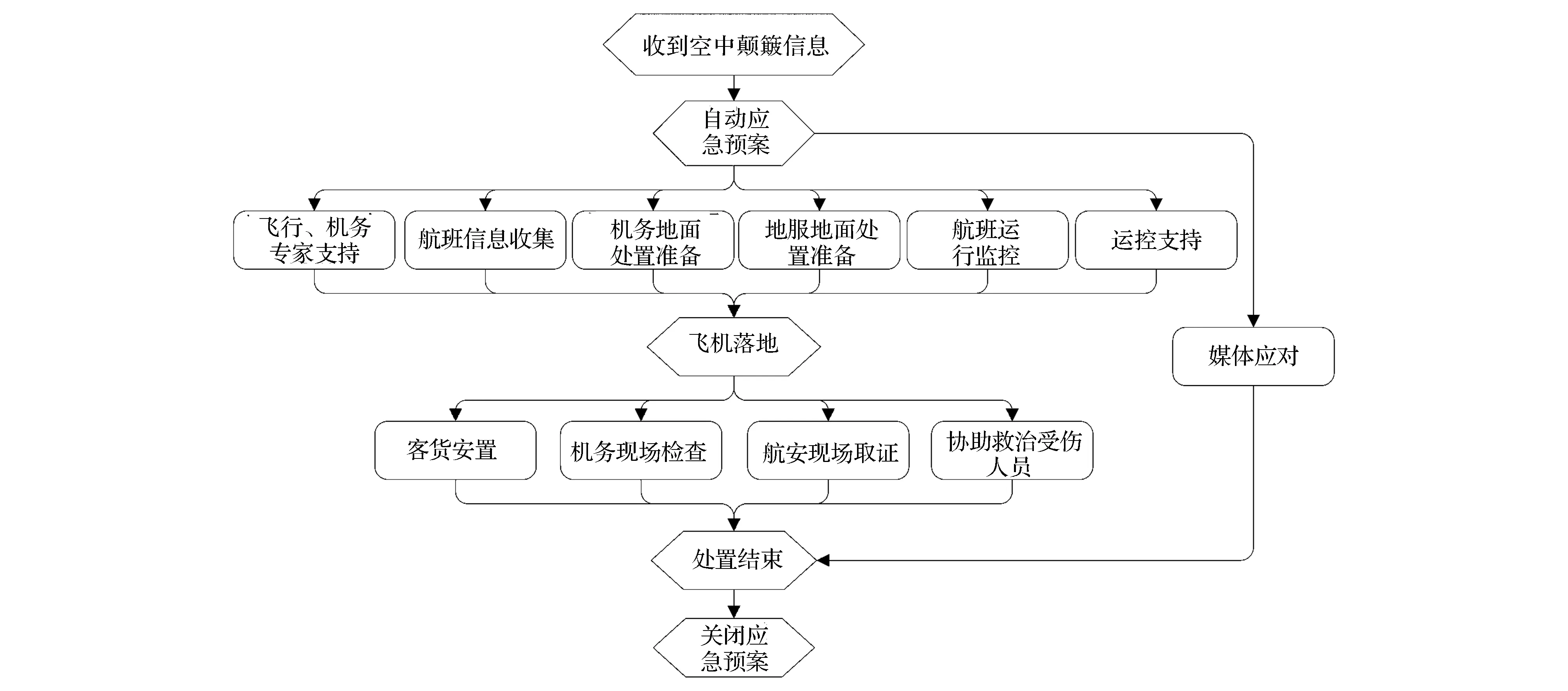
图5 航空公司空中颠簸应急处置流程
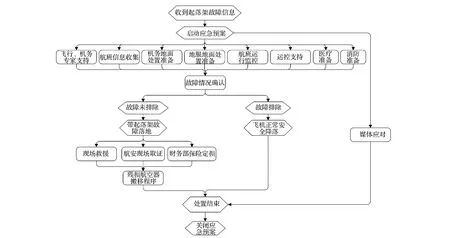
图6 航空公司起落架故障应急处置流程
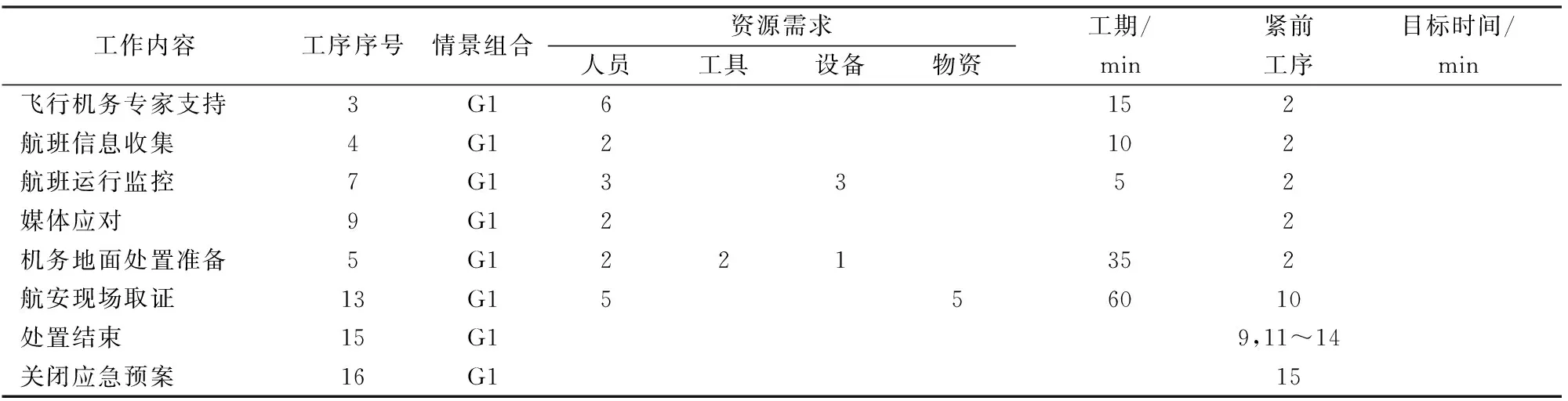
表1 合并为一次执行的工序及其参数
(2)需要多次执行的工序(见表2)

表2 需要多次执行的工序及其参数
(3)G1包含的工序和参数见附表3,G1组合后的结果如下:
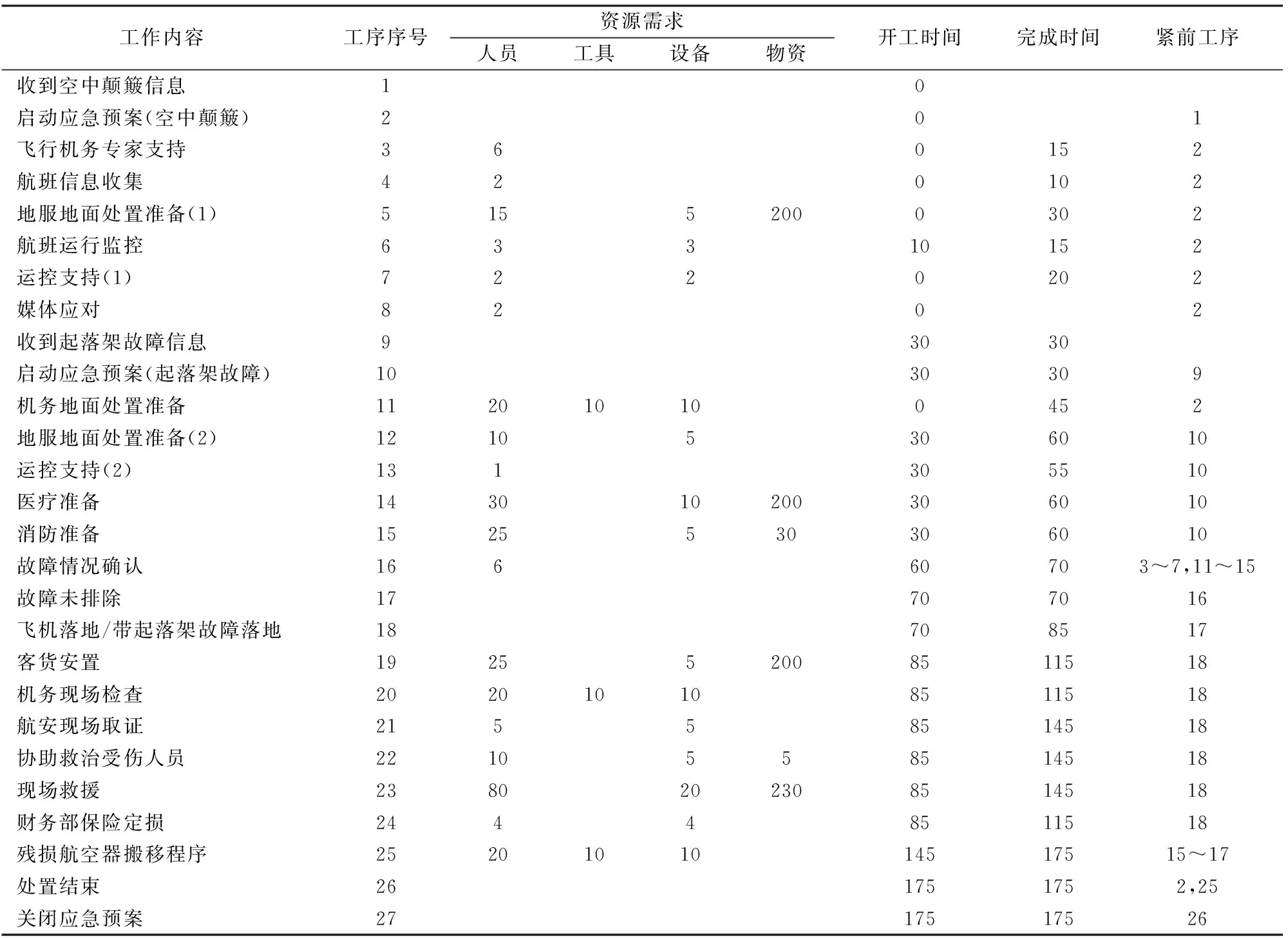
表3 情景组合G1的合并结果
同上,对G2=S11+S22进行合并,得结果如下:
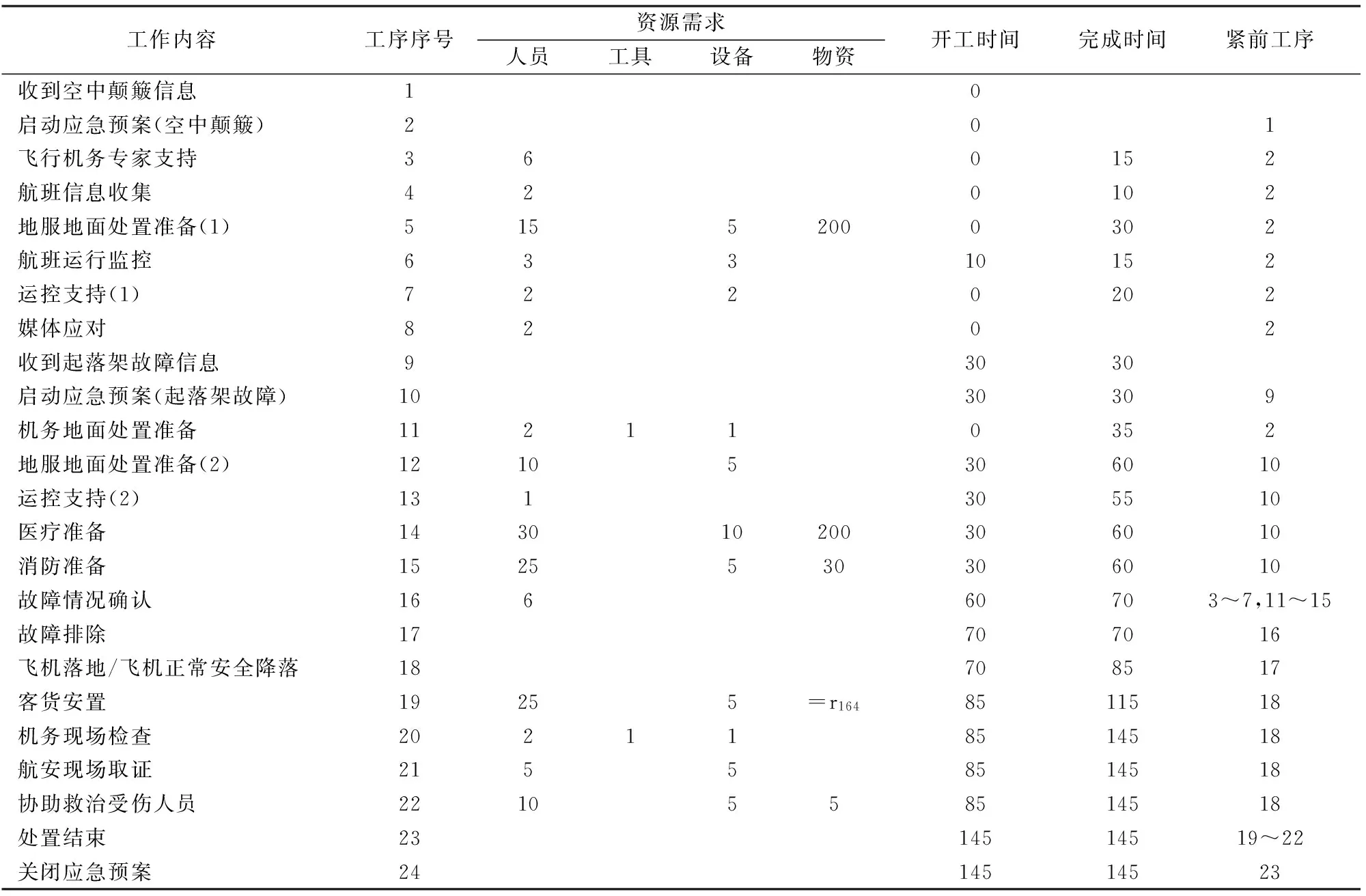
表4 情景组合G2的合并结果
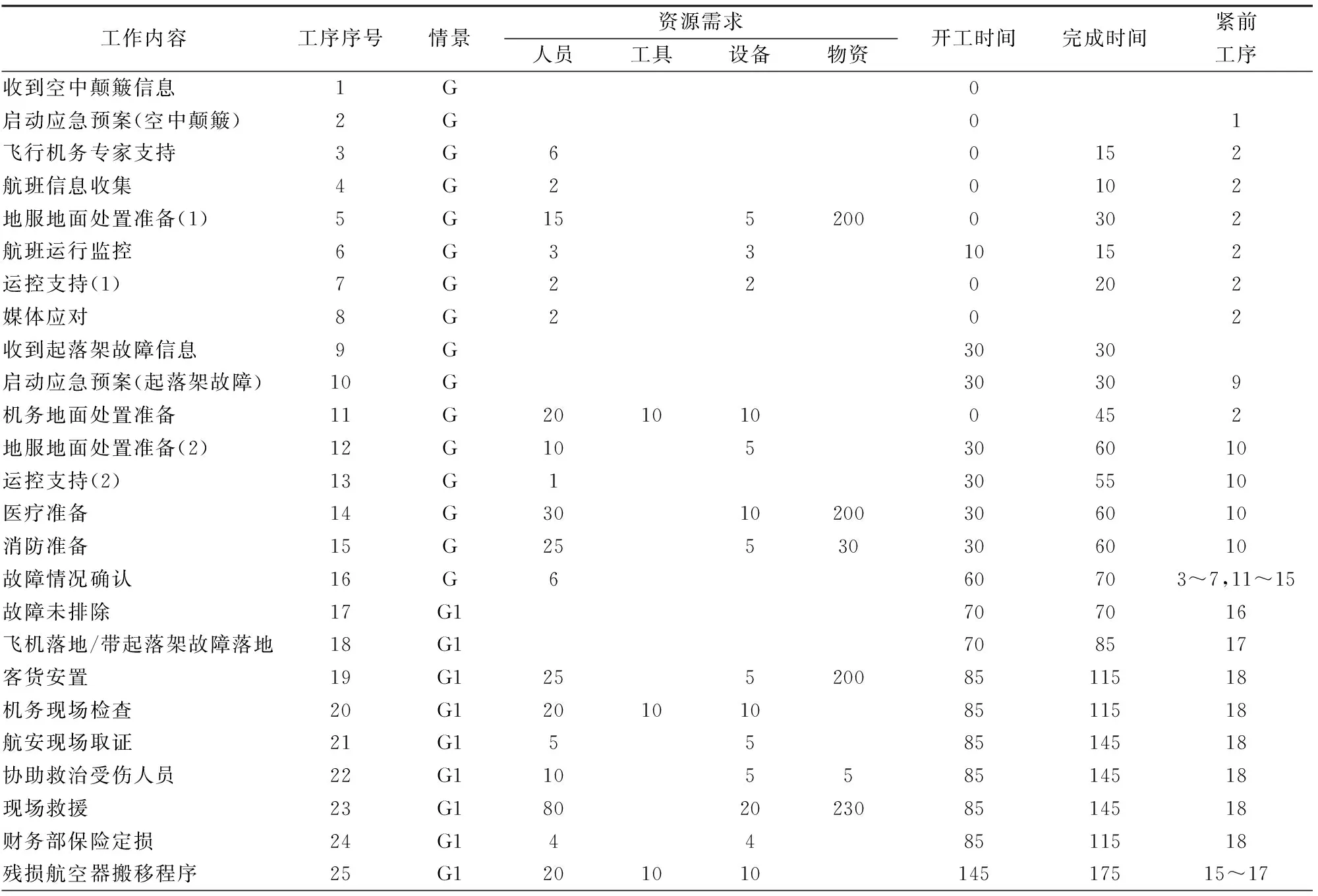
表5 G1+G2的合并结果
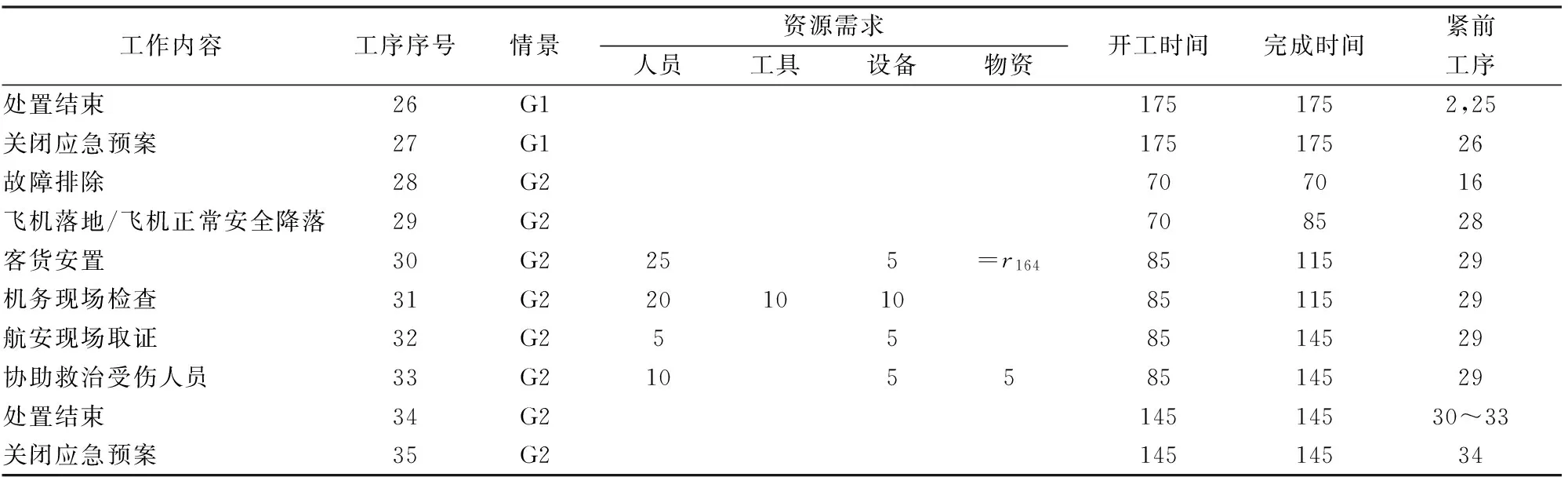
续表5
5.4 互斥情景之间的组合(G=G1+G2)
涉及的公共工序为“机务地面处置准备”。其他参数:ηG1=0.2,ηG2=0.8,k*=1,NG1,11,1=20,NG2,11,1=2;Φ1=0.9,Γ1=0.1。
由互斥情景组合的决策模型求解得出:rG,11,1*=20,rG,11,2=10,rG,11,3=10。
由并行情景组合的求解算法可以求解得出后续工序的安排如表5。在当前工序规模(小于100)下,求解过程用时平均仅数秒,与禁忌搜索等其他邻域搜索算法相比,搜索效率略高,解的质量基本一致。在工序规模超过1000时,本算法求解效率优势明显,在可接受求解时间内所得解的质量更优。
6 结语
本文研究设计了一种基于当前针对单灾种应急预案,通过计算机在线重构形式形成应对多灾种突发事件并发或次生时应急预案的方法。通过分析多类突发事件并发或次生时应急预案重构的主要问题和难点,针对并发和互斥两类典型情景组合问题构建了数学模型,并从应急管理的实际背景出发,在经典RCPSP问题基础上,增加了工序工期关联约束,将优化目标设定为工期和成本均衡的多目标问题,在传统串行调度算法的基础上,设计了基于工序关联分类的启发式算法,最后通过一个航空公司两类突发事件应急预案进行重构的示例对方法的应用做了说明。本文中将在线重构过程中部分存在搭接关系的工序进行合并、单独多次执行的预处理操作对应急管理者的在线操作能力提出了较高要求,在搭接关系复杂且工序内容边界不够清晰的情况下难于落地操作,未来将继续结合特定领域的应急管理实际,在现有序关系假设的基础上引入广义优先关系的网络计划,分析由于存在搭接关系带来的关键路径意义变化和新的求解算法。从而提升应急预案在线重构方式的效率和可行性。
[1] 祁明亮, 池宏,等. 突发事件应急管理专项报告[M]//中国科学技术协会.2007-2008管理科学与工程学科发展报告, 北京:中国科学技术出版社,2008:104-123.
[2] 吴宗之, 刘茂. 重大事故应急预案分级、分类体系及其基本内容[M]. 中国安全科学学, 2003,13(1):15-18.
[3] 于瑛英,池宏. 基于网络计划的应急预案的可操作性研究[J]. 公共管理学报, 2007, 4(2): 100-107.
[4] 于瑛英,池宏,高敏刚. 应急预案的综合评估研究[J]. 中国科技论坛, 2009,(02): 88-92.
[5]GeldermanJ,BertschV,TreitzM,etal.Multi-criteriadecisionsupportandevaluationofstrategiesfornuclearremediationmanagement[J].Omega, 2009, 37(1): 238-251.
[6] 刘吉夫, 张盼娟, 陈志芬, 等. 我国自然灾害类应急预案评价方法研究(Ⅰ):完备性评价[J]. 中国安全科学学报, 2008, 18(2): 5-11.
[7] 荣莉莉, 杨永俊. 一种基于知识供需匹配的预案应急能力评价方法[J]. 管理学报, 2009, 6(12): 1643-1647, 1686.
[8] 李永海,樊治平,袁媛. 基于相似历史案例分析的突发事件应急方案生成方法[J]. 系统工程,2014,(4):76-81.
[9] 温志强.政府职能转变视域下的突发事件应急决策模式创新研究[J]. 管理世界,2016,(5):176-177.
[10] 池宏, 计雷, 谌爱群. 由突发事件引发的 "动态博弈网络技术"的探讨[J],项目管理技术,2003,(1):12-14.
[11] 姚杰,计雷,池宏. 突发事件应急管理中大的动态博弈分析[J].管理评论,2005,17(3):46-50.
[12]QiMingliang,ChiHong,XuJGet.al.Astudyonselectingemergencycounterplaninuncertaintysituation[C]//Proceedingsof2008InternationalConferenceonManagementScienceandEngineeringManagement,Chongqing,China,2008: 711-716.
[13]BrysonKM,MillarbH,JosephcA,etal.UsingformalMS/ORmodelingtosupportdisasterrecoveryplanning[J].EuropeanJournalofOperationalResearch, 2002,141(3):679-688.
[14] 王庆全,荣莉莉,于凯. 一种基于范畴论的应急决策概念建模方法[J],情报学报,2009,28(6):929-938.
[15]QiMingliang,ChiHong,JiLei,etal.Astudyonthemethodforconstitutinganoperableemergencyplan[C]//ProceedingsofThe3rdInternationalConferenceonManagementandServiceScience,Beijing,September10-18,2009.
[16] 刘磊,池宏,邵雪焱,等. 预案管理中的重构问题研究[C]. 第四届国际应急管理论坛暨中国(双法)应急管理专业委员会第五届年会(ISEM’09), 北京, 2009-12-12.
[17]CormackAM,RusnakJ,BaldwinCY.Exploringthestructureofcomplexsoftwaredesign:AnempiricalstudyofopensourceandproprietaryCode[J].ManagementScience,2006,52 (7):1015-1030.
[18]EstrinG,BussellB,TurnR,etal.Parallelprocessinginarestructurablecomputersystem[J].IEEETransationsonElectronicComputers,1963,12(6): 747-755.
[19] 田军,李莉芳,白剑,等. 基于DSM的应急任务流程模块化设计研究[J],中国管理科学,2014,22(8):100-107.
[20]LiangYan,BaoJinsong,HuXiaofeng,etal.Aheuristicprojectschedulingapproachforquickresponsetomaritimedisasterrescue[J].InternationalJournalofProjectManagement,2009,27(6):620-628.
[21]SprecherA,HartmannS,DrexlA.Anexactalgorithmforprojectschedulingwithmultiplemodes[J].ORSpektrum,1997,19 (3):195-203.
[22]AkkanC,DrexlA,KimmsA.Networkdecomposition-basedbenchmarkresultsforthediscretetime-costtrade-offproblem[J].EuropeanJournalofOperationalResearch,2005,165 (2): 339-358.
[23]DeReyckB,DemeulemeesterE,HerroelenW.Localsearchmethodsforthediscretetime/resourcetrade-offprobleminprojectnetworks[J].NavalResearchLogisticQuarterly,1998,45 (6): 553-578.
[24]SalewskiF,SchirmerA,DrexlA.Projectschedulingunderresourceandmodeidentityconstraints:Model,complexity,methods,andapplication[J].EuropeanJournalofOperationalResearch, 102(1):88-110.
[25]KolischR,HartmannS.Heuristicalgorithmsfortheresource-constrainedprojectschedulingproblem:Classificationandcomputationalanalysis[M]//WeglarzJ.Projectscheduling:Recentmodels,algorithms,andapplications.Boston,KluwerAcademicPublishers,1999:147-178.
AStudyonEmergencyPlanReconstructionWithResourceConstraint
SHI Biao, CHI Hong, QI Ming-liang, LI Jia-lian
(Institute of Policy and Management, Chinese Academy of Sciences, Beijing, China,100190,China)
On the basis of the expression by the introduction of the network plan technique,the emergency disposal processes are added with resource types, quantity, and completion time constraints. The way to generate resource scheduling program is explored by computer on-line reconstruction. To satisfy the disposal need of many types of emergencies concurrent or secondary contingency, the quantity limitation and time-window of total resources constraints are considered in the model. The steps, objectives and considerations of the development in resource scheduling scheme are analyzed, and the models both in parallel and mutually exclusive scenarios are constructed, a heuristic algorithm is designed, using the contingency plans for reconstruction of the sample in an airline.
emergency plan; reconstruction; resources constraints
1003-207(2017)01-0117-12
10.16381/j.cnki.issn1003-207x.2017.01.013
2014-07-30;
2016-09-01
祁明亮(1976-),男(汉族),河南焦作人,中国科学院科技政策与管理科学研究所,副研究员,研究方向:应急管理,E-mail: mlqi@casipm.ac.cn.
C931.1
A

