股票质押式回购合约的动态质押率测算
任羽菲,杨成荣
(1.吉林大学商学院,吉林 长春 130012; 2.中国社会科学院研究生院,北京 102488;3.吉林大学数量经济研究中心,吉林 长春 130012)
股票质押式回购合约的动态质押率测算
任羽菲1,2,杨成荣1,3
(1.吉林大学商学院,吉林 长春 130012; 2.中国社会科学院研究生院,北京 102488;3.吉林大学数量经济研究中心,吉林 长春 130012)
本文首先运用期权定价理论建立了股票质押式回购在不同补仓方式下的质押率、融资期限、回购利差、交易费用以及警戒线和平仓线间的动态关系,然后以沪深300和中小300成分股为例,计算样本股在不同风险窗口期和补仓方式下的理论质押率,并借鉴失败效率思想,在既定管理目标下实证比较理论与实际质押率及平仓线折价质押率的风险覆盖能力。实证结果显示:不同风险窗口期内理论质押率大部分高于实际质押率,但现金补仓下理论质押率与实际质押率有相同的风险覆盖能力,股票补仓下理论质押率的风险覆盖能力低于实际质押率,高于平仓线折价质押率。据此,本文提出基于理论和实际质押率的组合模式来设定股票质押式回购合约的质押率。计算结果显示,组合质押率的风险覆盖能力优于理论质押率,融资成本降低方面优于实际分档质押率。因此,本文认为股票质押式回购质押率的设定应根据风险管理目标采用理论与实际质押率组合的模式,这既实现金融机构风控的目的也降低了回购方的融资成本。
股票质押式回购;质押率;风险覆盖能力
1 引言
股票质押式回购自2013年6月在上海及深圳证券交易所推出以来,在拓宽企业融资渠道和缓解企业融资难等问题上发挥着重要作用,并已成为证券行业重要的创新赢利点。根据Wind数据统计,截止到2014年6月在一年内股权质押融资的市场规模达到7761亿元,其中券商的股票质押式回购已达到3034亿元。在股票质押式回购交易过程中,证券公司首要解决的问题就是合理评定该业务的质押率以规避价格风险和信用风险。我国《股票质押式回购交易及登记结算业务办法》[1]规定“股票质押式回购的质押率上限为60%”,证券公司据此与客户协商来确定最终的质押率。根据沪深交易所的信息,股票质押式回购交易的平均质押率介于40%到66%之间,且有逐渐上升的趋势。因此,质押率的合理设定对证券公司开展该业务并进行有效风险管理至关重要。
关于质押融资业务的质押率,国内外学者从度量信用风险和违约损失视角进行了一系列探索。在信用风险度量方面,基于Merton[2]提出的结构化方法,Stulz和Johnson[3],Cossin和Hricko[4],王志诚[5], 沈传河、王胜文[6]等研究了质押物对质押担保债务定价的影响,且测算了质押物的质押率。基于Jarrow和Turnbull[7],Jarrow等[8],Duffie和Singleton[9]的简约式方法,Cossin和Huang Zhijiang[10]等在企业违约概率给定时,得到与银行风险承受能力相一致的质押率。在违约损失方面,李毅学、徐渝和陈志刚[11]通过损失的联合概率分布来确定股票质押贷款的质押率。王志诚等[12-13],范英和魏一鸣[14],黄中文等[15]给出我国股票质押贷款质押率评定的VaR方法,并实证分析其方法的可操作性。当质押物为存货时,张燃等[16]利用期权定价方法研究了库存质押贷款的质押率确定问题,并分析了质押率与贷款期限和贷款利率的关系。刘妍和安智宇[17]基于变现时间的VaR模型,研究流动性风险下存货质押贷款质押率的设定问题。孙喜梅和赵国坤[18]研究了简单二级供应链中存货质押融资的最优质押率问题,给出供应链信用水平下银行的最优质押率。陈云等[19]在延迟清算风险和内生流动性风险下,建立存货质押的多周期动态质押率模型。李富昌和王桦[20]在违约概率外生给定的假设下,建立存货质押率模型,并分析最优质押率和最大期望利润的影响因素。此外,Xia Jianming和Zhou Xunyu[21],Prager和Zhang Qing[22],Cai Ning和Sun Lihua[23],Chen Wenting等[24]利用期权定价原理,建立价格风险和利率风险下股票质押贷款合约的定价模型,并分析了合约价格的影响因素。根据对相关文献进行梳理可知,质押率的测算方法主要有结构化方法、简约化方法和VaR方法。简约化方法在测算质押率时需要较多的历史违约数据,故该方法应用到我国股票质押式回购合约中有一定局限性。VaR方法在风险控制上所具有的优势使其成为实际中常采用的质押率测算方式,然而该方法在计算时不易反映出合约条款对质押率的影响,如达到警戒线后不同的补仓方式对质押率的影响等。在实际中,证券公司根据客户融资需求设计合约条款,故不同条款对质押率的影响也是其关注的问题。结构化方式适于分析合约条款对质押率的影响,但相关研究主要从信用风险度量方面进行讨论,未能结合实际建立质押率与不同条款间的动态关系并评估质押率的风险覆盖水平。
本文的主要工作体现在:(1) 给定警戒线和平仓线,建立股票质押式回购合约质押率的决定方程,该决定方程给出了质押率与回购期限、回购利率、警戒线和平仓线之间的合理关系,这为该合约的条款设计提供技术支持。(2) 以沪深300和中小300指数的成分股为例,计算不同补仓方式下的理论质押率,并与实际质押率及平仓线折价质押率进行比较,其中实际质押率是中航证券公布的信息,平仓线折价质押率是根据王志诚[12]中的方法计算得到。(3) 借鉴Kupiec[25]提出的失败效率思想,通过不同风险窗口期的模拟回购实证比较理论、实际质押率和平仓线折价质押率的风险覆盖水平,进而根据金融机构的风险管理目标,采用理论和实际质押率的组合模式设定股票质押式回购合约的质押率。
2 问题描述及理论结果
2.1 合约分析和模型假设
我国股票质押式回购均设有警戒线和平仓线:当股价达到警戒线水平l时,资金融入方需进行补仓,即补充现金或增加质押股票至警戒线水平以上;当股价达到平仓线水平L时,资金融入方将被要求回购质押股票。设股票质押式回购合约的有效期为[0,T],质押股票初始价格为S0,融资额度为K,回购利率为γ。在交易之初,资金融入方将S0质押到第三方登记结算机构,缴纳总费用为c,该费用包括质押股票所在交易所向资金融入方收取的经手费,以及登记结算机构收取的质押登记费用。然后融入方将从证券公司得到K。在合约到期前,如果质押股票价格触及警戒线,即St≤lK,那么只要融入方进行补仓,该合约就不会被终止,否则会被平仓。如果质押股票价格继续下跌并触及平仓线,即St≤LK,那么融入方将被要求平仓。若融入方在规定时间内未能赎回股票,则融出方有权出售质押股票。如果合约到期前质押股票价格均未触及警戒线和平仓线,那么融入方到期可选择是否用KeγT赎回质押股票ST。
记股票质押式回购的质押率为ω,其中ω=K/S0。显然,警戒线、平仓线、回购利率、到期日以及补仓方式等均对质押率的确定产生影响,那么这些因素如何影响该合约的质押率?为建立质押率与这些因素之间的定量关系,下面从该交易的参与者权利、补仓条款以及质押股票的价格性质等方面给出本文所需的基本假设:
(A1)只要质押股票价格未达到平仓线,那么资金融入方就不能提前赎回股票。当融入方未能履约赎回质押股票时,融出方的权利仅限于出售质押股票。
(A2)当质押股票市值St达到警戒线lK时,资金融入方可通过补充现金αKeγT或增加质押股票βSt进行补仓,其中0 <α<1,β>1。如果股价下跌至平仓线LK,那么资金融出方有权出售质押股票变现,有l>L>1。
这里假定平仓后证券公司出售质押股票是基于下面的原因:与约定式回购相比,股票质押式回购可通过不转移股东控制权而进行融资,故当股价跌至警戒线时,资金融入方为保护其股东控制权会尽可能补仓。如果融入方选择平仓,那么就说明该回购交易违约的可能性更大。
(A3) 在风险中性概率Q下,质押股票价格{St}服从几何布朗运动:
(1)
其中r是无风险利率,δ是红利率,σ是波动率,Wt是标准布朗运动。
本文暂不考虑质押股票的流动性风险。这是因为,中国证券登记结算有限公司已公开股票质押的信息,并且根据《股票质押式回购交易及登记结算业务办法》,持股5%以上的股东进行该交易需及时披露信息,这就有助于证券公司规避质押股票的流动性问题。
2.2 质押率的理论结果
在分析警戒线和平仓线对质押率的影响时,通常用平仓线折价后的质押率作为股票质押式回购合约的理论质押率 (见王志诚[12-13]),这种方法不易刻画不同补仓方式对质押率的影响。本文通过分析资金融入方在警戒线和平仓线处的补仓行为,建立股票质押式回购合约理论质押率的决定方程。
设τ1=inf{t∈[0,T],St≤lK}表示警戒线点,τ2=inf{t∈[0,T];St≤LK}表示平仓线点。由(A3)知,Sτ1=lK,Sτ2=LK,0<τ1<τ2。当质押股票价格达到警戒线时,如果融入方进行补仓,那么在测算质押率时需要区分补充现金αKeγT和增加质押股票βSτ1两种情形。下面将在补仓和不补仓两种情形下,建立股票质押式回购合约质押率的决定方程。
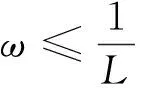
(1)
其中,N(x)是标准正态的累积概率分布函数,
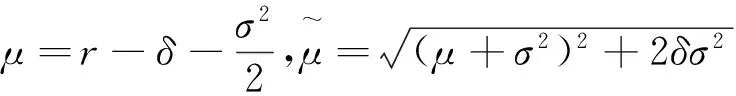
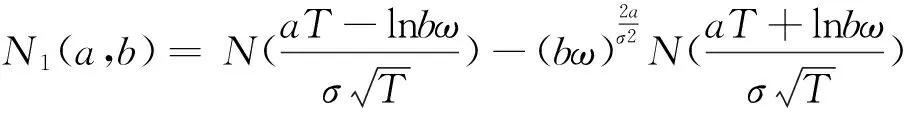
证明. 首先在初始时刻必有S0>LK,故ω V(S0,0)=e-rTEQ[(ST-KeγT)+1{τ2≥T}] +EQ[e-rτ2(Sτ2-KeγT)+1{τ2 由无套利原理知,1-ω+c/S0=V(S0,0)/S0,进而可得(1)式。 根据《股票质押式回购交易及登记结算业务办法》规定,警戒线水平不低于160%,平仓线水平不低于140%,故警戒线水平应满足l>eγT。下面两个定理分别给出现金补仓和股票补仓两种情形下质押率的理论结果。 (2) +(1-α)ωe-(r-γ)T[N1(μ,L)-N1(μ,l)] 其中Ni(a,b),i=1, 2的定义见定理2.1。 证明. 只需注意到股票质押式回购合约的初始价值为: V(S0,0)=e-rTEQ[(ST-KeγT)+1{τ1≥T}]+EQ[e-rT(ST-(1-α)KeγT)+1{τ1 然后利用无套利原理即得结论。 (3) 证明. 这时只需注意到股票质押式回购合约的初始价值为: V(S0,0)=e-rTEQ[(ST-KeγT)+1{τ1≥T}]+ EQ[e-rT((1+β)ST-KeγT)+1{τ1 EQ[e-rτ2((1+β)Sτ2-KeγT)+1{τ2 βEQ(e-rτ1Sτ11{τ1 表达式(1)-(3)分别给出了在不补仓,现金补仓和质押股票补仓三种情形下,质押率ω与回购利率、股价的波动率、回购期限、警戒线和平仓线水平之间的基准关系。根据表达式(1)-(3),证券公司可以针对不同的质押股票设计股票质押式回购合约。如,将回购期限长的合约分解为若干个期限不等的短期回购合约,每期回购质押率可以保持不变。 下面将以沪深300和中小300指数的成分股为例,根据质押率决定方程(1)-(3)计算理论质押率,再利用王志诚[13]计算平仓线折价的理论质押率,然后与中航证券公布的实际质押率[26]进行比较。为此,首先选择样本股并估计波动率。 3.1 样本选择及参数设定 根据《股票质押式回购交易及登记结算业务办法》,为确保样本股票的规模符合要求且有较好的流动性和行业代表性,本文在沪深300指数成分股和中小300指数成分股中选取样本,并采用Wind数据库中日收盘价的前复权数据计算收益率。样本区间选为2013年6月24日至2014年6月31日,并将其分为两部分:2013年6月24日至2013年12月31日作为第一部分,其数据用来参数估计;第二部分为2014年1月1日至2014年6月31日,其数据用作检验样本。在第一部分区间内,通过对样本股对数收益率的正态性检验,选出符合假设(A3)的股票,然后计算每只股票的理论质押率。第二部分区间的数据用来进行长度分别为1个月、3个月和6个月的模拟回购。由于各指数成分股不是固定不变的,故只保留本文数据区间内均入选成分股的股票,于是沪深300指数保留296只,中小300指数成分股300只全部保留。 首先,在第一部分区间内使用前复权收盘价计算日对数收益率,其公式为: ri,k=lnSi,k-lnSi,k-1 其中Si,k为第i只股票第k日的收盘价,k≤130,i表示沪深300的296只成分股和中小300的300只成分股。本文采用复权数据,故红利率δ=0。鉴于每只样本股的数据量>100,故选JB统计量在5%的显著性水平下进行正态性检验(何凤霞,马学俊[27])。根据检验结果,沪深300指数成分股中有60只股票通过正态性检验,中小300指数成分股中有87只通过正态性检验。另外,根据中航证券的信息,剔除该信息中未出现股票,其中沪深300剔除5只,中小300剔除15只。因此,本文最终确定这127只股票为样本股,且它们在第一部分区间内,股票价格均服从几何布朗运动。 为计算样本股的理论质押率,对每个样本股的对数收益率进行参数估计。本文采用极大似然(MLE)方法估计127只样本股的历史波动率,附录表A.1给出每只股票的年化波动率σ。 另外,本文设定回购期为半年,即T=0.5。根据上海银行间同业拆放利率的数据,将无风险年利率r设为5%;根据中航证券公布的信息,回购利率γ设定为8%(年复利)。根据上交所和深交所以及中国证券登记与结算有限公司的信息,每单位价值股票的费用c/S0取为0.01。 3.2 理论质押率与实际质押率的对比 在现金补仓和股票补仓两种方式下,通过Matlab软件计算样本股票动态质押率的理论值和对应的平仓线折价质押率,并与中航证券所公布的实际质押率对比。其中,平仓线折价质押率的计算公式如下: (4) 图1 不同波动率下理论质押率、平仓线折价质押率与实际分档质押率 (横轴是样本股的波动率,T=0.5,r=5%,γ=8%) 根据交易所规定,股票质押式回购交易中普通股票的质押率上限是60%,为方便比较不同计算方式下质押率对波动率的敏感性和风险覆盖水平,本文在计算理论质押率和平仓线折价质押率时未考虑该上限。 当α和β给定时,图1给出127只样本股的波动率对理论质押率和中航证券质押率的影响,其中横坐标是127只股票的波动率。注意到中航证券的质押率分为五档35%,40%,45%,50%,55%,从图1可以看出:(1) 中航证券的分档质押率对波动率不敏感,现金补仓和股票补仓的两种理论质押率都随着波动率的增加而降低,但平仓线折价的质押率随波动率没有明显的趋势变化特征,且存在较大的个股差异性。(2) 股票补仓的理论质押率高于中航证券的质押率,同时也高于现金补仓的理论质押率,但只是部分高于平仓线折价的质押率。(3) 当波动率低于48%时,现金补仓的理论质押率高于中航证券的质押率,并高于大部分平仓线折价质押率;当波动率高于48%时,现金补仓的质押率低于中航证券的质押率,且低于绝大部分平仓线折价质押率。这表明,在现金补仓情形下,对高波动率股票中航证券设定偏高的质押率,此时平仓线折价的理论质押率也偏高,这将低估股票价格风险,而对低波动率股票设定较高的质押率将导致资金融入方的融资成本升高。事实上,质押率决定方程(2)和(3)表明,样本股的波动率和补仓方式导致理论质押率间显著不同,且均与中航证券的分档质押率及平仓线折价质押率有显著偏离。 图1还显示,现金补仓的理论质押率在波动率48%处急速下降,这主要因为质押率ω是以非线性方式出现在质押率的决定方程(2)中。当回购期限为6个月时,质押率ω的速降点出现在σ=48%,当回购期限为1个月和3个月时,此点出现在σ=18%附近(见图3)。 再次根据质押率决定方程(2)和(3),对质押率产生影响的因素除波动率外,还有回购期限、回购利率以及设置的警戒线和平仓线等因素。图2和图3分别给出在现金补仓和股票补仓两种方式下,不同回购期限的理论质押率和中航证券的分档质押率随股票波动率的变化。由平仓线折价质押率的计算公式(4)可见,该质押率未能体现补仓方式对质押率的影响,故图2和图3中不包含平仓线折价质押率。 图2 现金补仓方式下不同波动率下的理论质押率 (横轴是样本股的波动率,r=5%,γ=8%) 在现金补仓方式下,图2显示合约的回购期限越长质押率越低,质押股票的波动率越高质押率越低。当回购期限在3个月以下,理论质押率均高于中航证券的质押率;当回购期限在9个月以上,理论质押率均低于中航证券的质押率。这暗示,如果按照中航证券的信息来设定质押率,那么3个月以下回购合约的资金融入方将增加融资成本;9个月以上回购合约的资金融出方可能会因低估质押股票的市场风险而遭受损失。 图3 股票补仓方式下不同波动率下的理论质押率 (横轴是样本股的波动率,r=5%,γ=8%) 在股票补仓方式下,图3显示,6个月以下回购合约的理论质押率均高于中航证券的分档质押率,并且这些理论质押率随着质押股票波动率的增加而降低,随着回购期限的增加而降低。这暗示,如果金融机构按照中航证券公布的质押率来开展股票质押式回购业务,那么在股票补仓方式下,该合约的资金融入方将大幅增加融资成本。 通过前面的对比分析可以看到,在两种补仓方式下,股票质押式回购合约的理论质押率、平仓线折价质押率与中航证券公布的质押率均有显著差异,那么在既定的风险管理目标下,金融机构选择哪种方式设定该业务的质押率呢?下面利用2014年1月到6月的检验样本数据,通过比较本文的理论动态质押率、平仓线折价质押率和实际分档质押率在这一时间区间的风险覆盖水平来对理论质押率模型进行评价。 由于股票质押式回购是通过质押股票来降低和规避该业务的信用风险,故在扣除自身的市场风险后,质押率应保证质押股票的价值在回购期限内不低于回购额的某个目标水平。基于这种风险覆盖程度的考虑,本文借鉴Kupiec提出的针对VaR的失败效率检验思想,设定金融机构的管理目标线,通过计算实际价格低于融资额的目标线水平的次数来衡量理论质押率和中航证券的质押率的风险覆盖水平。具体计算步骤如下: 第三步,在风险窗口期内,第i只股票若出现一次收盘价Pi,t 显然,当利用击穿频率刻画质押率的风险覆盖水平时,如果击穿频率高,那么该质押率的风险覆盖水平就低,反之则认为风险覆盖水平较高。 表1和表2分别给出沪深300和中小300的样本股在不同回购期限和不同目标线水平下的击穿频率和被击穿的个股数,其中l=135%表示以不击穿该平仓线水平作为金融机构的管理目标。 表1显示出在给定的风险窗口期内,股票补仓方式下质押率的击穿频率高于现金补仓下质押率和中航证券的质押率的击穿频率,但低于平仓线折价质押率。这表明,股票补仓方式下的理论质押率风险覆盖水平较低,而平仓线折价质押率的风险覆盖水平最低。同样的结论适用于中小300的样本股,这通过表2可以看到。 鉴于平仓线折价质押率风险覆盖能力欠佳,下面将主要分析理论质押率和实际分档质押率。表1和表2显示,当金融机构的管理目标线低于平仓线时,两种补仓方式下理论质押率的击穿频率与中航证券分档质押率的击穿频率相差不大。特别是,现金补仓下的理论质押率与中航证券分档质押率的击穿频率几乎相同。结合图2和图3,当理论质押率和中航证券分档质押率的风险覆盖水平相当时,金融机构完全可以适当提高股票质押式回购合约的质押率,这不但可降低资金融入方的融资成本,同时有助于金融机构开发更多的客户。 以3月期的股票质押式回购为例,当警戒线水平为150%,平仓线水平为135%,管理目标线水平为110%时,如果合约规定资金融入方以补充现金的方式补仓,那么金融机构可设定该合约质押率为现金补仓理论质押率。由于3月期现金补仓方式的质押率高于中航证券分档质押率,但两者的风险覆盖水平相同,故金融机构增加了更多该业务的客户,同时客户也降低了其融资成本。 以6月期的股票质押式回购为例,同样是以增加现金方式补仓,那么当质押股票的历史波动率低于48%时,金融机构可设定合约质押率为理论质押率;当质押股票的历史波动率高于48%时,金融机构按照中航证券分档质押率来设定。这种组合设定质押率的模式,可以保证不击穿管理目标线水平110%,同时也降低资金融入方的融资成本,同时又为金融机构带来更多该业务的客户。类似地,对于股票补仓方式下质押率的设定也可以采用这种组合设定模式。 通过观察表1和表2,在现金补仓方式下,随着回购期限的增加,该理论质押率的风险覆盖水平也逐步提高;在股票补仓方式下,随着回购期限的增加,相应理论质押率的风险覆盖水平却在降低。这样的结果主要是因为,股票补仓方式尽管增加了质押品的价值,但同时质押股票的市场风险也增加了。一旦质押股票波动率有变化,就会马上反应到质押品的价值变化上,进而就会导致质押率的风险覆盖能力降低。 由表1和表2还可以看到,如果金融机构是以平仓线为管理目标,那么1月期股票质押式回购合约的质押率适于采用中航证券的分档质押率来设定。以表2为例,中航证券分档质押率的击穿频率为0,而其他两种理论质押率的击穿频率都高于1%,特别是现金补仓方式下理论质押率的击穿频率高达5%左右。 表1 不同目标线下沪深300指数成分股模拟回购的击穿频率统计 表2 不同目标线下中小300指数成分股模拟回购的击穿频率统计 表3 组合质押率在不同目标线下的击穿频率统计 基于样本数据,在保证质押率的风险覆盖能力和降低融资成本的前提下,本文给出理论质押率和实际分档质押率的一种组合方式: (5) 其中ωc是组合质押率,ωt为理论质押率,ωp实际分档质押率,ψi>0,i=1,2是调整项,可根据金融机构风险管理的目标、补仓方式和回购期限进行调整。组合方式(5)表明:当ωt和ωp的差额适当大时,须对理论质押率进行负向调整;当差额较小时可直接采用理论质押率;当差额为负时,则须对理论质押率做正向调整。 结合前面的分析以及表1和表2的结果,在股票补仓方式下选择ψi=0.5,i=1,2;在现金补仓方式下,回购期限T小于半年,或回购期限为半年且波动率σ≤0.48时,选择ψi=0.3,i=1,2。表3给出采用该组合质押率的模拟回购在不同管理目标线下的击穿频率。由表3可见,在既定风险管理目标下,与理论质押率相比,该组合质押率的风险覆盖能力明显提高;与实际分档质押率相比,采用该组合质押率降低了资金融入方的融资成本,这将有助于金融机构拓展股票质押式回购业务的规模。 通过在不同风险窗口期对理论和实际分档质押率,以及组合质押率风险覆盖能力的对比分析,本文认为金融机构在设定股票质押式回购合约的质押率时,应以分档质押率为基础,充分考虑自身的管理目标,结合质押股票的波动率大小和回购期限的长短,采用单一质押率或组合质押率的设定模式,以便在提高风险覆盖能力的同时,降低资金融入方的融资成本。 因篇幅所限,本文仅就样本数据给出理论质押率与实际质押率的一种组合方式,后续将围绕组合质押率的优化问题开展进一步研究。 本文首先在不同补仓方式下建立股票质押式回购合约的质押率、警戒线、平仓线、回购期限、回购利率、质押股票的波动率以及股票质押手续费等之间的动态关系,即质押率的决定方程。然后,以沪深300和中小300的成分股为例,根据质押率的决定方程计算样本股在不同的回购期限和补仓方式下的理论质押率,并将其与平仓线折价质押率、中航证券的分档质押率进行了对比分析。结果表明,实际的分档质押率对波动率不敏感;两种补仓方式下理论动态质押率均随着波动率的增加而降低,随着回购期限的延长而降低,且现金补仓下理论质押率和分档质押率均低于股票补仓的理论质押率;平仓线折价的质押率随波动率没有明显的趋势变化特征,且存在较大的个股差异性。另外,本文基于失败效率思想,在不同管理目标下实证比较了股票质押式回购的理论质押率、平仓线折价质押率和实际质押率的风险覆盖能力。实证结果显示,在既定管理目标和不同回购期下,现金补仓的理论质押率大部分高于实际分档质押率,且两者风险覆盖能力相当;股票补仓的理论质押率均高于实际质押率,风险覆盖能力比实际质押率略低,但比平仓线折价质押率要高,这表明平仓线折价质押率的风险覆盖水平最低。由于实际分档质押率对质押股票的波动率和回购期限不敏感,故采用分档质押率有可能高估或低估质押股票的市场风险,进而导致增加回购方的融资成本或者增加金融机构的风控成本。对此,本文基于理论质押率和实际质押率,提出股票质押式回购合约质押率设定的一种组合模式。结果表明,该组合质押率的风险覆盖能力优于理论质押率,融资成本降低方面优于实际分档质押率。因此,本文认为金融机构在设定风险管理目标后,应采用两种补仓方式下的理论质押率与实际分档质押率组合的模式,这样既能保证质押率的风险覆盖能力,同时又能降低回购方的融资成本。 附录: 表A.1 沪深300和中小300成分股的历史波动率 [1] 深圳证券交易所, 中国证券登记结算有限责任公司. 股票质押式回购交易及登记结算业务办法(试行)[EB/OL].[2013-05-24].www.szse.cn/main/disclosure/bsgg-font/39749894.shtml. [2] Merton R C. Theory of rational option pricing[J]. Journal of Economics and Management Science, 1973, 4(1): 141-183. [3] Stulz R, Johnson H. An analysis of secured debt[J]. Journal of Financial Economics, 1985, 14(4): 501-521. [4] Cossin D, Hricko T. A structural analysis of credit risk with risky collateral:A methodology for haircut determination[J]. Economic Notes, 2003, (2): 243-282. [5] 王志诚. 用期权定价原理分析抵押贷款的信用风险[J].金融研究, 2004, (4): 95-105. [6] 沈传河, 王胜文.证券质押贷款的期权定价方法与银行风险分析[J].现代乡镇, 2005,(8): 11-13. [7] Jarrow R, Turnbull S. Pricing derivatives on financial securities subject to credit risk[J]. Journal of Finance, 1995, 50(1): 53-85. [8] Jarrow A, Lando D, Turnbull S. Markov model for the term structure of credit risk spreads[J]. Review of Financial Studies,1997,10(2):481-523. [9] Duffie D, Singleton K. Modeling term structure of default table bonds[J]. Review of Financial Studies, 1999, 12(4): 687-720. [10] Cossin D, Huang Zhijiang, Aunon-Nerin D,et al. A framework for collateral risk control determination [R]. Working Paper, European Central Bank, 2003, 1: 1-47. [11] 李毅学, 徐渝, 陈志刚.股票质押业务的贷款价值比率[J].系统工程, 2006, 24(10): 55-58. [12] 王志诚, 赵士波,田昆,等.股票质押贷款的实证研究[J].经济科学, 2002,(1): 73-84. [13] 王志诚. 股票质押贷款质押率评定的VaR方法[J].金融研究, 2003, (12): 64-71. [14] 范英, 魏一鸣.基于基差VaR的股票组合质押率评估方法[J].系统工程, 2003, 21(4): 86-89. [15] 黄中文, 刘亚娟, 朱芳芳.股票质押贷款业务及质押率探析[J].金融理论与实践, 2009, (9): 92-95. [16] 张燃, 徐爽, 王凤敏. 质押贷款质押率决定的期权定价方法[J]. 中国管理科学,2013,21(1):16-22. [17] 刘妍, 安智宇. 考虑流动性风险的存货质押融资质押率的设定[J]. 中国管理科学, 2014, 22(S1): 324-328. [18] 孙喜梅, 赵国坤. 考虑供应链信用水平的存货质押率研究[J]. 中国管理科学, 2015, 23(7): 77-84. [19] 陈云, 刘喜, 杨琴. 基于清算延迟和流动性风险的供应链存货质押率研究[J]. 管理评论, 2015, 27(4): 197-208. [20] 李富昌,王桦. 基于存货选择决策的存货质押率模型[J]. 中国流通经济,2016,30(1): 114-121. [21] Xia Jianming, Zhou Xunyu. Stock loans[J]. Mathematical Finance, 2007, 17(2): 307-317. [22] Prager D, Zhang Qing. Stock loan valuation under a regime-switching model with mean reverting and finite maturity[J]. Journal of Systems Science and Complexity, 2010, 23(3): 572-583. [23] Cai Ning, Sun Lihua. Valuation of stock loans with jump risk[J]. Journal of Economic Dynamics and Control, 2014, 40(3): 213-241. [24] Chen Wenting, Xu Liangbin, Zhu Songping. Stock loan valuation under a stochastic interest rate model[J]. Computers and Mathematics with Applications, 2015, 70(8): 1757-1771. [25] Kupiec P H. Techniques for verifying the accuracy of risk measurement models[J]. Journal of Derivatives, 1995, 3(2): 73-84. [26] 中航证券股票质押的信息公告[EB/OL]. http://www.scstock.com/main/invest/CreditTransaction/gpzy/bdzqzsl/index.shtml. [27] 何凤霞, 马学俊. 基于R软件的正态性检验的功效比较[J]. 统计与决策, 2012, (18): 17-19. Dynamic Loan-to-Value Ratios of Stock Pledged Repos REN Yu-fei1,2,YANG Cheng-rong1,3 (1. School of Business, Jilin University, Changchun 130012, China;2. Graduate School of Chinese Academy of Social Sciences, Beijing 102488, China;3. Center for Quantitative Economics of Jilin University, Changchun 130012, China) Stock pledged repos are important innovative financial products in China, and its loan-to-value (LTV) ratios are crucial for risk management of financial institutes.In this paper, dynamic relationships among key parameters of stock pledged repos, such as loan-to-value ratios, predetermined termination lines, maturity date, repos interest rate and fees are established, by using option pricing theory. Then theoretical LTV ratios of sample stocks with different maturities are given by these dynamic relationships, in which samples are chosen from constituent stocks of Shanghai-Shenzhen 300 and SZSE SME 300 Price indexes in China. Furthermore, under different target levels of risk management and different maturities, these theoretical LTV ratios are compared to practical ratios published by ZhongHang Security and the LTV ratio discounted by closing line, and empirically investigated risk coverage levels of these theoretical and practical LTV ratios based on Kupiec’s idea. Empirical results show that most theoretical LTV ratios with different positions are higher than the practical one, while theoretical LTV ratios with cash margin have the same risk coverage level with the practical one, and the risk coverage level of theoretical LTV ratios with the supplementary stocks term is lower than practical ones, but higher than LTV ratios discounted by closing line. Therefore, a kind of combined mode with theoretical and practical LTV ratios are proposed in this paper. The empirical result shows that the risk coverage level of the combined LTV ratio is higher than theoretical LTV ratios. Besides, they are quite superior to practical LTV ratios in aspect of cutting financing cost. Therefore, it is argued that, with financial institutes’ management target lines, LTV ratios of stock pledged repos should be set to combined modes with theoretical and practical LTV ratios in order to control risk and reduce financing costs. Our conclusion is helpful for financial institutes to expand the scale of stock pledged repos and control the risk of these repos. stock pledged repos; loan-to-value ratio; risk coverage level 1003-207(2017)01-0035-10 10.16381/j.cnki.issn1003-207x.2017.01.005 2014-04-24; 2016-07-15 国家自然科学基金资助项目(71201069);教育部人文社会科学重点研究基地自选项目(JLUCQE14018);吉林大学基本科研业务费项目(2016zz009) 杨成荣(1974-),女(汉族),吉林人, 吉林大学商学院副教授,研究方向:金融工程,E-mail:yangcr@jlu.edu.cn. F830.9 A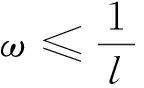
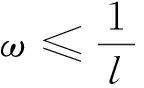
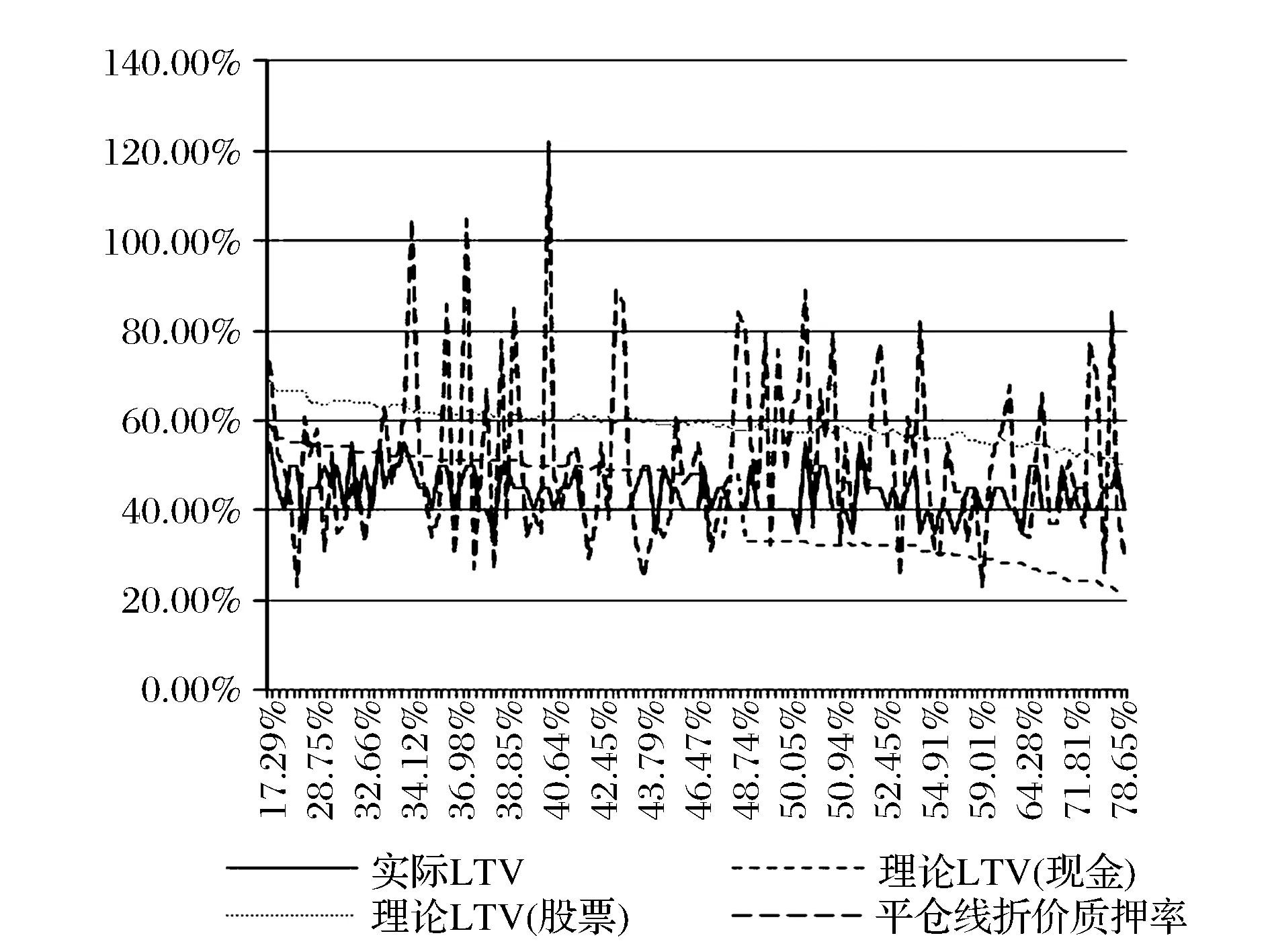
3 与实际质押率的对比分析
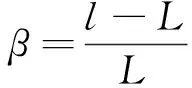
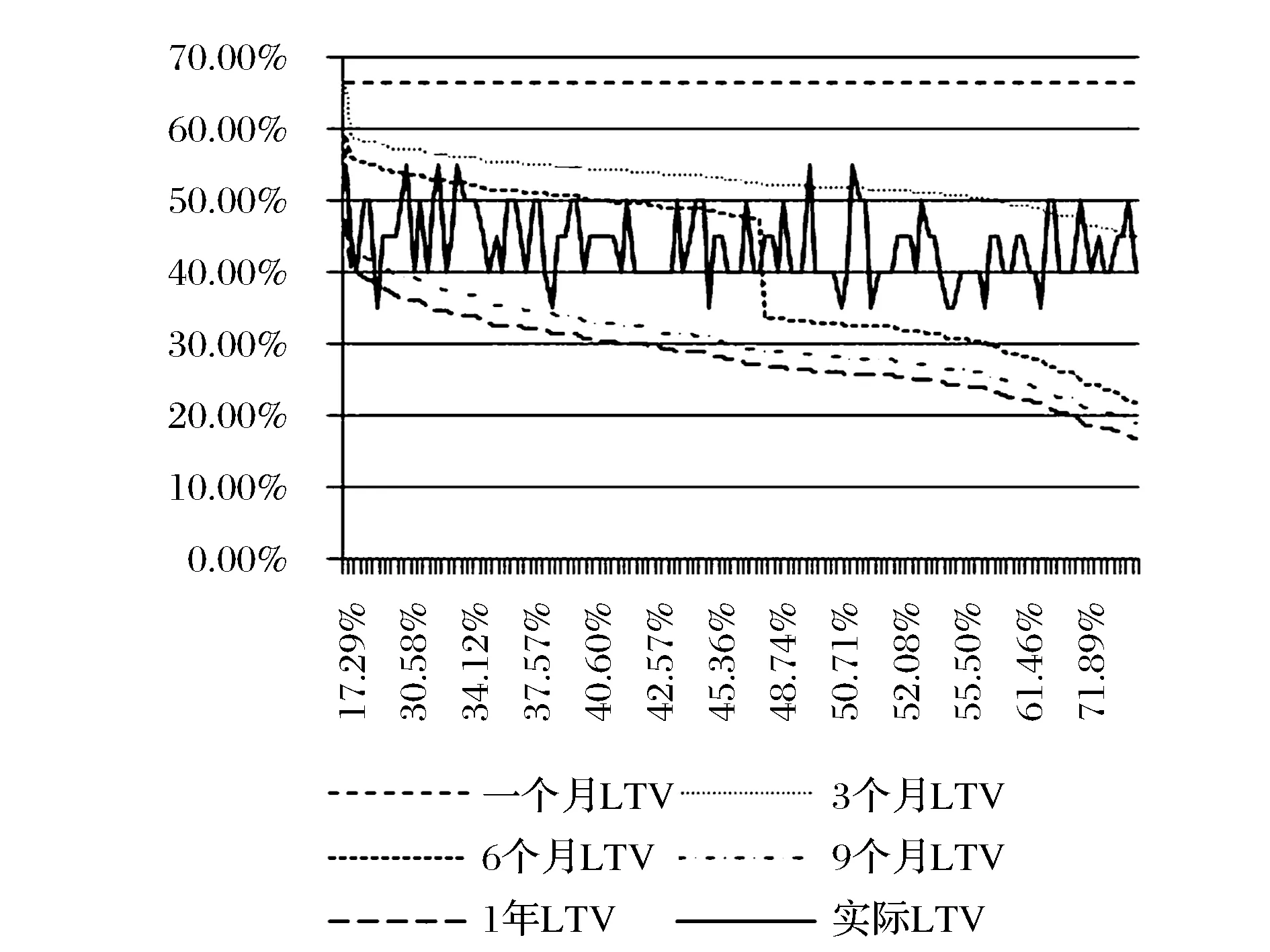

4 理论质押率模型评价
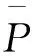
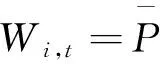



5 结语

——杭州:警示教育常抓常新

