岩溶管道径流公式研究

谢杨

摘要：如何准确计算地下水在岩溶-裂隙管道中的径流成为了岩溶含水层地下水计算和模拟的关键，虽然目前国际上使用较为广泛的岩溶管道模拟方法Conduit Flow process（CFP）相比传统的等效多孔介质渗流计算方法在计算精度上有了很大的提高，但该方法仍然忽略了岩溶管道发育形态特征，仅将管道截面概化为圆形，且计算时未分流态。针对CFP法存在的上述问题，本研究从管道形成及形态特征入手，对岩溶管道径流公式进行研究，该方法在岩溶径流计算及岩溶裂隙含水层地下水渗流计算具有广泛应用前景，为相应数值模拟软件开发提供了理论基础。

Abstract： How to accurately calculate the Karst-fractured groundwater runoff has become the key of the karst groundwater calculation and simulation. Although Conduit Flow process （CFP） widely used internationally compared with the traditional calculation method of equivalent porous media seepage in calculation precision has been greatly improved， this method still ignore the morphological feature of Karst conduits development， only defines the circular cross section of the conduits， and the calculation does not flow. Aiming at the problems of CFP， this study from the tube formation and morphological characteristics， takes a research on Karst runoff formula. This method has a broad application prospect in the Karst runoff calculation and Karst-fractured groundwater seepage， providing a theoretical basis for the corresponding numerical simulation software development.

关键词：公式推导；岩溶管道流；截面概化；流速公式

Key words： formula derivation；karst conduit flow；cross section summarizing；flow velocity formula

中图分类号：P641 文献标识码：A 文章编号：1006-4311（2017）09-0196-03

0 引言

我国有世界上最大的岩溶区，广泛分布于西南、东北地区，尤其是西南地区的岩溶区，岩溶管道广泛发育，研究岩溶管道渗流，对指导西南巖溶区生产实践具有重要的意义。

直径大于10mm的空隙称为岩溶管道[1]。国内外水文地质工作者进行了大量的研究，研究成果按时间顺序大致可以分成三个阶段：等效多孔介质法、多重叠加法、Conduit Flow process（CFP）法。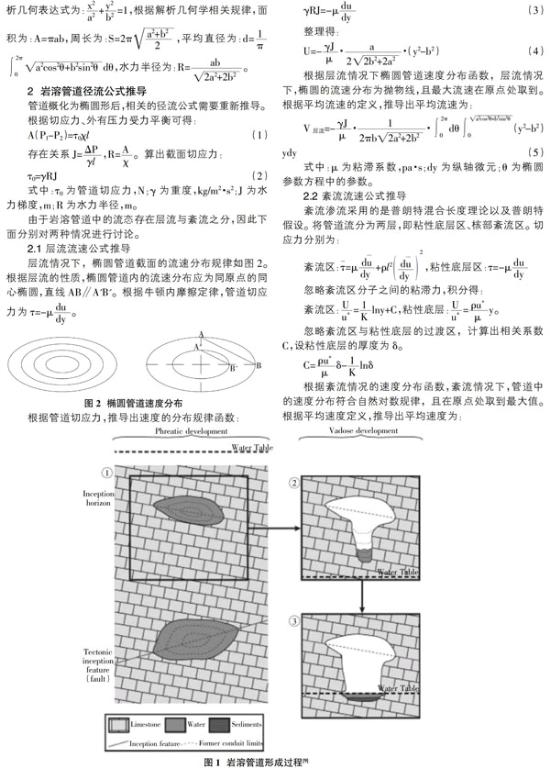

20世纪90年代初提出的多孔介质等效法[2]，将岩溶管道等效为渗透系数较大的多孔介质管道，使用达西定律求解[3]，该方法只适用于半径很小且低雷诺数径流的岩溶管道，而当雷诺数超过10后该方法的计算精度将急剧下降。同样，多重介质叠加法[4]将影响管道流的各种因素绘制成场，使用计算机叠加计算，忽略中间径流过程，只考虑起始端流速与结束端流速，该方法受人为影响因素较多。而美国地质调查局于2007年提出Conduit Flow process（CFP）法[4]，并以该方法为基础基于Modflow开发岩溶管道径流数值模拟计算模块，将管道流公式进行有限元差分计算，经水文地质工作者验证[5，6]，该方法相比之前的两种方法具有较高计算精度，因此，该方法广泛应用于岩溶管道模拟计算[7，8]。

虽然CFP法在岩溶管道径流计算上取得了一定的进步，但是管道径流公式仍然采用的是圆形截面推导且层流、紊流计算公式不分，与真实情况相差很大。本文将以岩溶管道形成的地质成因为基础，将岩溶管道截面重新概化，并推导该情况下的管道径流的层流、紊流公式。

1 岩溶管道截面的概化

CFP法中将管道截面概化为圆形，与真实岩溶发育形态特征具有较大差异，因此本文将从岩溶管道形成的水文地质条件及岩溶管道发育形态特征出发，将岩溶管道截面概化成椭圆形，使得管道截面形态更接近于自然界岩溶管道形态特征，从而提高岩溶管道径流计算精度。

大量研究及实际岩溶调查研究表明岩溶管道的发育与裂隙有关[9]（（图1），根据实地踏勘与国外水文地质工作人员的研究可以总结为三个阶段：①裂隙低于潜水水位，地下水顺着碳酸盐岩的裂隙流动，并进行溶蚀，形成一个椭圆形截面的管道；②随着地壳的抬升或者侵蚀基准面的下降，地下水开始溶蚀椭圆形截面的管道底部，形成一个底部有水，上部为空腔的，截面类似于蘑菇的空腔管道；③由于地下水溶蚀，管道中的水达到侵蚀基准面，纵向溶蚀作用变缓，开始侧向侵蚀，并发生沉积，形成一个截面类似于哑铃的空腔管道。

上述三个阶段中，由于在第二、第三阶段岩溶管道中形成了空腔，且管道一般较大，即通常所说的地下暗河，对于大管道径流，目前使用明渠径流的相关理论进行研究，不属于本文研究的岩溶管道类型。本文重点研究上述第一阶段发育的岩溶管道中的径流公式及计算。

2 岩溶管道径流公式推导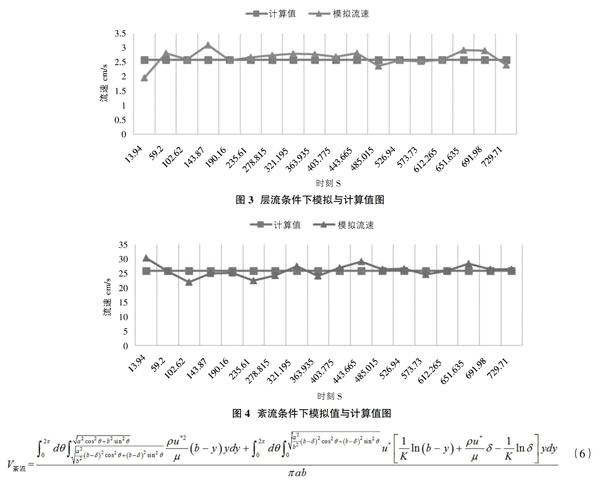

由于岩溶管道中的流态存在层流与紊流之分，因此下面分别对两种情况进行讨论。

2.1 层流流速公式推导

3 模拟结果

使用ANSYS fluent进行模拟计算，并于实验数据在Excel中进行汇总对比，见图3、图4。

4 结论

本文从岩溶-裂隙管道發育几何形态特征入手，分别推导了椭圆截面岩溶管道的层流、紊流公式。使用数值模拟软件对该公式进行验证。从图3和图4中可以发现，计算值与使用软件模拟计算值相差不大，是一种比较可靠的计算方法。综上所述，将岩溶管道截面概化为椭圆形，且层流、紊流公式分开计算，精度高于原CFP中管道流公式。

参考文献：

[1]PARDO-IG ZQUIZA E， DUR N J J， ROBLEDO P， et al. Fractal Modelling of Karst Conduits [J]. Mathematics of Planet Earth， 2013， 217-220.

[2]陈崇希.岩溶管道一裂隙一孔隙三重空隙介质地下水流模型及模拟方法研究 [J].地球科学—中国地质大学学报，1995，20（4）：361-366.

[3]洪淑娜，蓝俊康，陈丽娜.基于GMS的模拟结果绘制岩溶区地下水位等值线图 [J].中国农学通报，2013，29（29）：113-117.

[4]SHOEMAKER W B， KUNIANSKY E L， BIRK S， et al. Documentation of a Conduit Flow Process （CFP） for MODFLOW-2005 [M]. U.S Department of the Interior，U.S Geological Survey， 2007.

[5]CHANGA Y， WUA J， LIUB L. Effects of the conduit network on the spring hydrograph of the karst aquifer [J]. Journal of Hydrology， 2015， 52（7）：517-530.

[6]SALLER S P， RONAYNE M J， LONG A J. Comparison of a karst groundwater model with and without discrete conduit flow [J]. Hydrogeology Journal， 2013， 21（7）： 1555-1566.

[7]KARAY G， HAJNAL G. Modelling of Groundwater Flow in Fractured Rocks [J]. Procedia Environmental Sciences， 2015， 25：142-149.

[8]张蓉蓉，束龙仓，星闵，等.管道流对非均质岩溶含水系统水动力过程影响的模拟[J].吉林大学学报（地球科学版），2012，42（2）：386-392.

[9]RONGIER G， COLLON-DROUAILLET P， FILIPPONI M. Simulation of 3D karst conduits with an object-distance based method integrating geological knowledge [J]. Geomorphology， 2014， 217：152-164.