独立学院静电场高斯定理教学

周挽平

摘要：本文介绍在独立院校中，如何在学生数理基础差学时有限的条件下，讲授静电场高斯定理。我们建议尽量利用图示法证明，简化曲面积分的定义，以及适当增加对称性分析。

Abstract： This paper introduces how to teach the Gauss theorem of electrostatic field in the independent colleges， where the mathematica and physics of the students are weak. We propose to make use of the graphic method as far as possible， to simplify the definition of surface integrals， as well as to appropriately increase the symmetry analysis.

关键词：独立学院；静电场高斯定理；图示法

Key words： independent college；the Gauss Theorem of electrostatic field；graphic method

中图分类号：O211.4 文献标识码：A 文章编号：1006-4311（2017）09-0193-03

1 静电场高斯定理的教学要求与困难

大学物理是理工科必修的公共基础课程。但由于独立学院处于向职业教育转型过程，许多学校的大学物理课程面临课时减少的问题。另外高考人数逐渐减少，录取率逐年提高。昔日的精英教育已经变成大众教育（湖北省2016年本科录取率达到49%[1]，全国录取率（包括高职专科）预计超80%[2]）。独立学院的新生基础必然非常薄弱。如何使高考处于及格线附近的学生在较短的时间内掌握必要的物理知识，是大学物理教师必须面对的问题。本文尝试在对大学物理中一个非常重要的章节-静电的高斯定理进行分析，讨论如何实现以上目标。

静电的高斯定理的麦克斯韦四大电磁学方程之一[3]，结合麦克斯韦环路定理能唯一的确定电场的性质。该定理在电磁理论中非常重要，它揭示静电磁的基本性质-有源性。对于理解整个麦克斯韦电磁理论是不可或缺的，在2006年颁布的《非物理类理工学科大学物理课程教学基本要求》[4]中属于A类。通过对静电的高斯定理的学习，能加深学生对于场的物质性的理解，也能了解物理学对场的研究方法。对后期学习磁场的高斯定理也有所帮助。现有的教学中，静电的高斯定理一般安排2个学时。在2个学时内需要教学目标我们分为3个：①准备阶段（建立概念：电场线电通量（其中包含：匀强电通量、曲面电通量、闭合曲面电通量、单位法向量）电荷密度（球对称、面对称、柱对称））；②静电场高斯定理的证明阶段，③应用阶段（分析适用条件，对称性分析，举例）。要在规定学时内完成以上任务需要教师对教材非常熟悉，并且学生要较好的数学物理基础并精神高度集中。如果在教学中其中任意一个知识点，教师处理不当或学生没有跟上。则整节课教学效果必然大打折扣。另外该节课涉及预备的理论基础为：矢量分析，曲面积分，库仑定律。由于该知识点讲授一般在大一下的期中之前，大部分高校的矢量分析与曲面积分没有学习。这使静电的高斯定理讲授变得异常困难。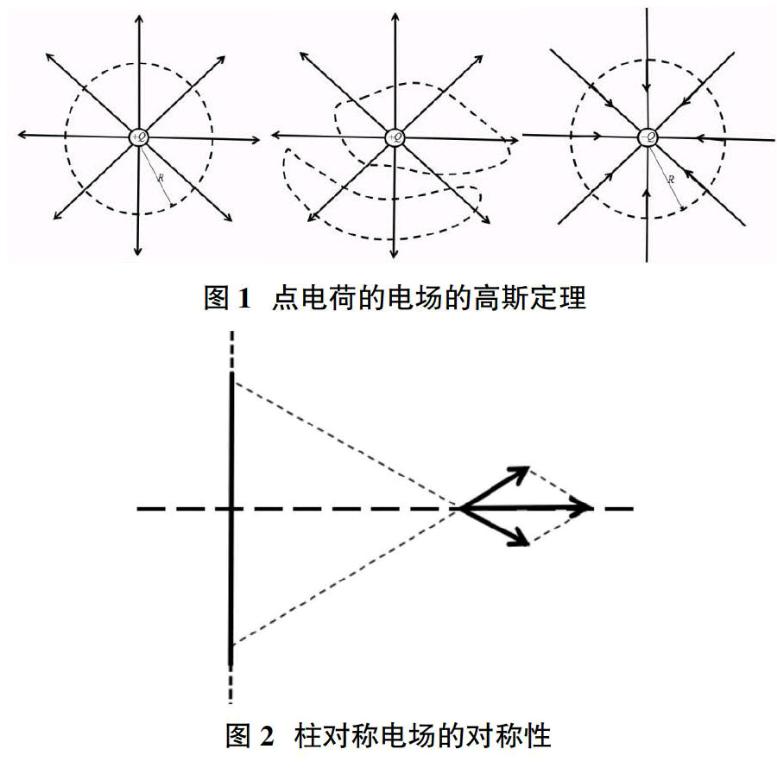

但是抛开理论上的繁琐，静电的高斯定理的几何图像特别清晰。如果适当的放弃理论的严谨性，可以使大部分基础薄弱的学生掌握高斯定理，并能提高他们的学习信心。对于基础好的学生，可以通过启发式教学引导自学更加严谨的证明。我们认为对于不需要电磁理论的专业，这样安排是合理的。对于电子通讯等专业，学生在大三要学习后继课程《电磁场与电磁波》。那时学生的理论基础也足够来学习那门新课程。本文以下分为三个部分，第2部分讨论高斯定理的预备知识讲解和证明。第3部分为讨论高斯定理应用讲解。第4部分为讨论的总结。

2 静电场高斯定理的准备和证明

静电场高斯定理证明一般从引入电场线的概念开始，而这个知识点是学生高中非常熟悉的，因此我们一般快速带过。主要是复习电场线分布与场强关系，让学生通过图片回顾下几种典型电荷分布的电场线。然后介绍电通量的几何概念-“穿过曲面的电场线的数量”。这里和最终的表述不同，我们希望通过逐步的讲解，深化学生对这个概念的理解。首先以匀强电场为例，引入电通量的定义式。当电场与平面垂直，面积越大，场强越强电场线越密，通量越多。因此定义Φe=N=E ┴ S。当电场与平面存在夹角，则引导学生通过投影法，或矢量分解法得到Φe=EScosθ。强调夹角与通量正负的关系为后面封闭曲面做准备。虽然处理方法普通，但我们一般在这个地方花较多时间，启发引导学生。这样的引入可以加深学生对通量的理解。

对于非匀强场的通量的计算，简单的介绍思想就可以了。由于通量对应电场线数量。任意曲面的通量，可以分解为无数面积元通量之和。这里的定义涉及曲面积分，对于大一的学生来说数学基础还无法处理或计算。我们通常以一个x-y平面上矩形区域为例介绍通量的计算。这是通常的2重积分，也是在大学物理课程中学生能计算比较复杂的非匀强场通量的问题。通过这个具体的例子，学生的理解会更加深刻。对于闭合曲面，我们规定傳出的通量为正，得到电通量的几何意义：穿出曲面与穿入曲面电场线的数量差。非匀强场的通量涉及数学较多，因此以教师讲解为主。对于一般的曲面积分则可以引导基础较强的学生思考通过投影法如何写成定积分的表达式。

静电场的高斯定理适用条件，可以通过选择题、判断题来得到。顺便考察学生对定理的理解。

3 静电场的高斯定理的应用

静电场的高斯定理的求解电场的局限性很大，讲解高斯定理的应用是为加深学生对高斯定理的理解。而这里的讲解也是分为①用静电场的高斯定理求解电场条件；②对称性分析；③具体计算。

首先是要给出高斯定理的求解电场的条件：只有存在某个高斯面过带求场点，满足：①电场垂直高斯面并大小不变，或者②电场与高斯面处处平行。满足这个条件高斯定理可以简化为ES┴=。电场的求解就可以由积分方程化简为简单的代数计算了。在这里要强调：S┴可以是高斯面的一部分，Qin是高斯面内的电荷。我们可以通过设问“什么样的电荷分布满足以上条件呢？”我们引入对称性分析。

通常的高斯定理的应用主要是求球对称、柱对称、面对称三种电荷分布下的电场。受到学时的限制，一般的教材在对称性的分析上用的时间很少，没有给出球对称、柱对称、面对称的定义，并且电场的分布和方向一般是直接给出的[5，6]。失去了知识的内在联系，也使学生缺少对称性这方面的锻炼。首先我们给出电荷球对称、柱对称、面对称的定义。球对称是指电荷分布相对某个球的任意直径有旋转不变性。例如：均匀带电的球体球面满足球对称。柱对称是指电荷分布相对某个轴具有旋转不变性，并且相对轴的方向有平移不变性。例如：无限长均匀带电的圆柱体圆柱面。面对称是指电荷分布沿某个平面上任意方向平移不变。例如无限大均匀带电的平面。通过这些定义提出课外思考：有没有非均匀的带电体满足以上的条件，并求出电场的表达式。

由电荷对称得到电场分布对学生来说是比较困难的。我们认为通过图像来表达会更加容易。学生的理解也更加深刻。对于柱对称的无线长均匀带电直线（图2）。由于对称点上在待求场点的垂直电场相互抵消，合场强垂直直线。电场空间分布可以绕直线旋转得到。因此电场大小只与距离有关。

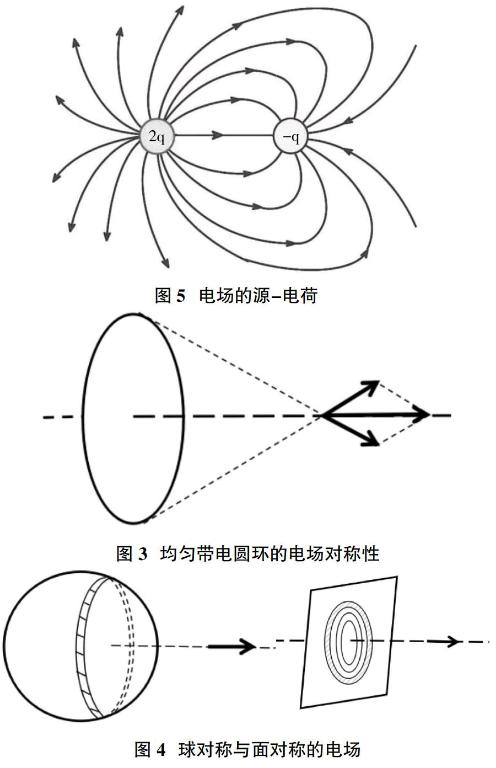
对于球对称和面对称。先分析均匀带电圆环轴线上的场强（图3），由于对称点上在待求场点的垂直电场相互抵消，合场沿着轴线。

球对称或面对称的电荷总是可以分解为无限个均匀带电同轴圆环（图4），合场沿着轴线。因此，球对称电荷电场必然沿着半径方向。电场空间分布可以通过旋转得到，因此电场大小只与距离有关。而面对称的电荷的电场必然垂直平面。

在具体计算场强时候，我们认为应该避免直接利用抽象的曲面积分求解。在推导过程中要强调的要点是曲面必须是闭合曲面。特别在柱对称和面对称中，强调高斯面应该包含柱体的底面和侧面。在具体讲解中另一个学生容易出现问题的地方就是高斯面包围电荷的计算。我们在作业和考试中经常发现学生不能正确写出球体球壳体积，因此在课堂上计算更加复杂的非均匀分布的电荷电场的求解效果也不会好。相应的问题可以留在习题课上深入讨论或者作为学有余力的同学作为课外练习。

4 讨论与总结

静电场高斯定理的几何图像非常清晰。通过我们的讲授学生基本能够掌握定理的内容。

但是提到有源场的概念，学生又会比较迷糊。这由于学生第一次接触静电场是有源场的概念，我们认为很有必要说明有源场的意义加深他们的印象。通过展示图5的电场线，我们指出有源场的概念在中学中就已经提出并要求学生给出：电场线从正电荷出发终止于负电荷，这也是静电场高斯定理定性的描述。静电场高斯定理定量的结果是给出，从正电荷产生或在负电荷终止的电场线的数量与电荷量成正比。我们再通过将正电荷-电场线-负电荷与水源-水流-出口类比，表明电荷是电场线的源和闾，这也是电场是有源场的含义。

在静电场高斯定理中我们可以补充一点近代物理的知识来提高学生的兴趣、扩大他们的视野。静电场高斯定理是由库仑定律推导而来，它们两个本质上是源于光子的静质量为零。与静電场类似，引力也是平方反比力。牛顿引力可以证明是满足高斯定理，引力的源是物质的质量。现代物理认为引力子的静质量为零。最近发现的引力波[7]波速为光速正是引力子的质量为零的要求。如果某种粒子的静质量不为零，对应场不满足高斯定理，场本身可以产生或吸收场线。例如：汤川秀树当年寓言的介子[8]。

静电场高斯定理在静电学中与许多知识点有关联。比如：①电场叠加原理；②静电平衡电荷分布，电场分布；③求电容电场；④积分法求典型带电体的电势；⑤类比建立磁通量概念。其中①是为了分析电场对称性以便用该定理求电场，所以在准备时，最好在前一节课就得到均匀带电圆环和直线的电场。对于②⑤，主要是对定理的理解，通过以上的教学，学生完全可以接受。对于③④，可以作为静电场高斯定理应用的延续。如果教学时间充足可以精讲。也可以简单的套用本节的结论来精简课堂，例如用电场叠加原理求平行板电容电场。

我们认为匀强电场通量的计算，通量的几何意义，以及静电场高斯定理的几何意义，是本节课的重点。难点是几个应用：面积元通量求和，高斯定理求电场，高斯定理求电荷。考虑到学生的专注力与数学物理基础较差，在本节课中应强调重点，既概念的建立。具体的应用是为了增加学生的理解。我们在给学生建立概念尽量结合图像，并尽量用较短的词句描述。

整个教学过程中我们用到图示法，类比法，启发式，讨论法，将难点尽可能分多步骤解决，并绕开抽象的定义和计算。最终使大部分学生能理解并能应用静电场高斯定理。

参考文献：

[1]罗欣，张晨昕.今年我省本科实际录取率约49%[N].楚天都市报，2016-8-15（2）.

[2]三晋直播.高招调查：2016年高考全国录取率预计超80%[OL].http：//mt.sohu.com/20160603/n452679670.shtml， 2016-06-3.

[3]郭硕鸿.电动力学[M].北京：高等教育出版社，1997，19-24.

[4]教育部高等学校非物理类专业物理基础课程教学指导分委员会.非物理类理工学科大学物理课程教学基本要求[J].物理与工程，2006（05）：1-8.

[5]马文蔚.物理学[M].五版. 北京：高等教育出版社，2006.

[6]屠庆铭.大学物理[M].二版.北京：高等教育出版社，2006.

[7]B. P. Abbott et al. Observation of Gravitational Waves from a Binary Black Hole Merger[J]. Phys. Rev. Lett. 2016， 116， 061102.

[8]褚圣麟.原子物理学[M].北京：人民教育出版社，1979，323-326.