采用变结构动态贝叶斯网络的交通流量预测*

王永恒，高 慧，陈炫伶

湖南大学 信息科学与工程学院，长沙 410082

采用变结构动态贝叶斯网络的交通流量预测*

王永恒+，高 慧，陈炫伶

湖南大学 信息科学与工程学院，长沙 410082

物联网和大数据流式计算的快速发展为智能交通系统的研究带来新的机遇。交通流量预测一直是智能交通系统的关键问题。针对交通流量预测中一个固定模型无法适应多种环境的问题，以及面向数据流的模型更新问题，提出了一种基于变结构动态贝叶斯网络的交通流量预测方法。该方法以复杂事件处理和事件上下文为基础，通过上下文聚类进行历史数据的划分，并通过事件流在线聚类支持聚簇的更新。面向不同聚簇的数据，采取搜索-打分的方法学习对应的贝叶斯网络结构，基于高斯混合模型实现贝叶斯网络的近似推断。在线预测时根据当前上下文选择合适的模型或模型组合进行预测。真实和仿真数据上的实验结果表明，该方法能够获得比当前常用方法更好的预测效果。

智能交通系统；交通流量预测；复杂事件处理；变结构动态贝叶斯网络

1 引言

近年来，随着物联网（Internet of things,IoT）和移动计算技术的迅速发展，人们加速跨进大数据的时代。很多应用快速产生多种多样的数据，对这些数据进行实时高效的处理能够获取更大的价值。对数据流的实时处理是大数据研究的一个关键，大数据特性中的快速性（velocity）和多样性（variety）正是对这种情况的刻画。

作为物联网中间件的核心及大数据流式处理的关键技术，复杂事件处理（complex event processing，CEP）正在受到广泛的关注。复杂事件处理是对数据流中的原始事件进行解释和组合，从而识别出更高层的复杂事件（也称复合事件）的过程[1]。复杂事件处理技术在很多领域得到了广泛应用，如基于无线传感网的环境监测、股票走势的连续分析等。近期大数据的流式计算技术也得到了快速发展，如Apache的Storm、Spark Streaming及Flink等项目，这些项目强调高效处理大规模分布式数据流，但并不直接支持复杂的操作。把这些技术和复杂事件处理配合起来使用，能够更好地支持分布式数据流的高效和智能处理。

物联网和大数据流式处理技术的发展，为智能交通系统（intelligent transportation system，ITS）带来了新的发展机遇。借助物联网技术，可以对交通信息进行全方位的感知和数据传输。机遇大数据流式处理技术，可以对产生的大量数据进行实时和智能的处理。交通流量预测作为很多交通智能决策的依据，在智能交通系统中占据重要的位置。

人们对交通流量预测问题进行了大量研究，开发了多种预测模型和方法。近年来比较成功的有基于支持向量机的方法[2-3]、基于深度学习的方法[4-5]、基于贝叶斯网络（Bayesian network，BN）的方法[6-8]和基于混合模型的方法[9]等。基于贝叶斯统计技术，贝叶斯网络能够很好地把领域知识和数据融合起来，支持不完整数据的处理及因果分析，并能够较好地解决过拟合的问题。这些特点使得贝叶斯网络在预测模型中占据重要位置，并在交流流量预测中获得广泛应用。

当前的交通流量预测方法还存在以下问题：（1）当环境变化时，一个固定的模型无法在不同的环境下都具备良好的预测能力[9]。基于混合模型的方法能够在一定程度上克服这个问题，避免在环境变化时出现很糟糕的预测结果。但模型组合方法无法保证在每种环境下能够得到最好的结果。（2）现有的方法基本都是从大量历史数据中训练模型，然后把模型用于实时的预测，而很少考虑随着新数据的产生，模型也可能需要发生相应的变化。（3）随着物联网和移动计算的发展，人们能够实时获取多种环境信息，如路况、天气等。现有的交通预测方法往往还是根据有限的信息进行预测，而没有综合利用各种实时的环境信息。

针对上述问题，本文提出了一种基于变结构贝叶斯网络（structure varying dynamic Bayesian network，SVDBN）的交通流量预测方法。本文方法以复杂事件处理和事件上下文为基础，通过上下文聚类对数据进行划分，针对不同的数据学习对应的贝叶斯网络模型，并在对事件流预测的过程中实时更新模型。在预测时针对当前上下文选择合适的模型或模型组合进行预测。贝叶斯模型的结构学习基于搜索-打分的方式实现，近似推断通过高斯混合模型（Gau-ssian mixture model，GMM）来实现。真实和仿真数据上的实验结果表明，本文方法能够获得比当前常用方法更好的预测效果。

2 相关研究

2.1 复杂事件处理

复杂事件处理技术通过对原始事件流的持续监视获取高层的复杂事件。Luckham和Etzion等人介绍了复杂事件处理的基本概念和处理结构[1,10]。复杂事件处理的核心是复杂事件处理网络（event processing network，EPN），它通过事件通道把多个复杂事件处理代理（event processing agent，EPA）、事件产生者、事件消费者等连接起来。

与本文相关的一个研究方向是上下文敏感复杂事件处理。针对上下文的表示人们研究了多种模型，一般认为本体是表示上下文的最佳模型。为了表示不确定知识，近期有人采用模糊本体来表示上下文。Zhang等人提出了一种基于模糊集的领域本体构建方法，在本体概念属性集上引入了模糊集隶属函数[11]。Cai等人在其著作中阐述了模糊本体的隶属度和典型性问题，并研究了模糊本体模型在上下文表示和推理中的应用[12]。

另一个重要的相关研究是预测式复杂事件处理（predictive complex event processing），也就是预测将来某个事件的发生。Etzion等人在其著作中指出，预测式复杂事件处理的目标主要是为了防止或减缓某个事件的发生[10]。Fülöp等人提出了一个预测式复杂事件处理框架[13]，实际上是在复杂事件处理网络中增加预测分析模块。在这个框架下，很多已有的预测分析技术可以直接应用于预测式复杂事件处理，但这些方法如何适应大规模的分布式数据流，以及如何调整模型适应数据的变化，仍然是待解决的问题。

2.2 交通流量预测

交通流量预测的相关模型和方法非常多，Eleni等人对短时交通流量预测技术进行了详细的综述[14]，对常见的模型和方法进行了分类对比，并提出了短时交通流量预测的10项挑战及对应的研究工作。

最近随着深度学习热潮的兴起，涌现出了一些基于深度学习的交通流量预测工作。Huang等人提出了一种基于深度信念网络（deep belief networks，DBN）进行交通流量预测的方法。该方法下层采用深度信念网络，最上层采用回归模型进行最终的预测[4]。同时其最上层的回归模型支持多任务学习（multitask learning）。Lv等人在其基于深度学习的交通流量预测中使用了自编码器（autoencoder）来学习交通流量的一般特征，并采用贪婪逐层融合的方式进行训练[5]。深度学习的方法能够取得较好的预测效果，但模型训练比较复杂，也容易出现过拟合的问题。

与本文直接相关的是贝叶斯网络方面的研究工作。Sun等人采用贝叶斯网络模型进行交通流量预测，在建模事实数据和待预测数据结点的联合分布时采用了高斯混合模型[6]。其中高斯混合模型的参数通过竞争性EM算法（competitive expectation maximization，CEM）实现。Castilloa等人使用贝叶斯网络进行起点-终点及链路的交通预测，采用高斯模型进行联合分布建模[7]。同时在给定起点-终点流量的情况下，采用了随机用户平衡（stochastic user equilibrium，SUE）的方式进行链路流量处理。Zhu等人也是把SUE融合到贝叶斯网络模型，把链路流量作为起点-终点流量的父结点[8]。根据先验路段流量确定所有变量的先验分布，然后通过更新一些观测的路段流量，给出后验分布，从而实现最终预测。和本文相比，这些研究都没有考虑交通数据发生大的变化时，模型无法适应的问题。同时也没有考虑面向数据流的模型更新问题。

3 系统结构

3.1 总体框架

系统总体框架如图1所示。首先定义复杂事件处理网络中的各概率事件处理代理（probability event processing agent，PEPA）的事件模式、相互连接及事件上下文的获取规则。来自传感器网络或其他系统的原始事件，经复杂事件处理网络处理后形成复杂事件流，并保存在历史数据库中。模型训练时首先对历史数据按时间片进行划分，然后以时间片为单位，根据事件上下文进行离线聚类，对每个获得的聚簇分别学习对应的贝叶斯网络结构和参数。在线预测时，对在线复杂事件流进行基于上下文的在线聚类，根据聚类的结果选择一个贝叶斯模型或多个贝叶斯模型的组合来进行预测。同时，在线聚类的结果能够实时更新聚簇的数据，在此基础上进行贝叶斯模型结构和参数的实时更新。

Fig.1 System architecture图1 系统总体框架

3.2 复杂事件处理和上下文

原始事件是指某个时刻某个事情的一次发生，例如传感器的一次数据读取产生一个原始事件。原始事件表示为＜A,T>，其中A为事件属性的集合，T为事件发生的时标。如果为不确定事件，则表示为＜A, T,P>，P为事件的概率。复杂事件是由原始事件或者复杂事件按照一定的运算规则形成的事件，表示为＜E,R>，其中E是复杂事件的组成元素，R为事件合成规则。如果是不确定事件也加上概率。具有相同特征的一类事件为一个事件类型。复杂事件有多种模式，如ALL、ANY、COUNT、SEQ等，这些在文献[10]中有详细的定义和说明。例如在交通领域可以使用COUNT模式获取一定范围内的车辆总数，用SEQ获取车辆行驶路线等。这些模式可以进一步组合和嵌套形成更复杂的模式。作为本文的基础，作者前期开发了一个分布式概率复杂事件处理系统（distributed probabilisticcomplexeventprocessingmethod，DPCEP）[15]。

事件上下文定义为一些特殊的条件，根据这些条件可以对事件实例进行划分，从而使被划分的事件能够关联在一起来处理[10]。上下文有很多类型，如“汽车旅馆M1周围2公里范围”是一个距离上下文，“公路交通状态是缓慢行驶”是一个状态上下文。通常上下文的获取有两种情况：一种是简单情况，直接通过事件的属性获取上下文，例如车辆的行驶速度。另外一种是复杂情况，需要通过定义复杂事件来帮助获取上下文。例如道路拥堵上下文的获取可以通过道路流量计数、车辆行驶速度和等待时间等多个因素结合起来进行判断。

定义2（模糊本体）在特定领域D上的模糊本体O表示为OD=(C,R,P,I)。其中C为模糊概念的集合，P为概念的模糊属性的集合，I是概念实例的集合，R是模糊角色（也就是对象及概念间的关联）的集合。

Fig.2 Apart of traffic domain ontology图2 交通领域本体的一部分

例如“红色轿车”是一个模糊概念，它是另外一个概念“轿车”的子集。“张三非常喜欢跑车”是一个模糊角色的实例，关联程度是“非常高”。模糊属性“驾驶速度”的值可以表示为{“S(慢)”，“M（中）”，“F（快）”}。本文采取手工方法建立了一个交通领域模糊本体，其中的一部分如图2所示。本体的表示基于Fuzzy OWL 2（http://gaia.isti.cnr.it/～straccia/software/ FuzzyOWL/）。关于上下文敏感复杂事件处理的详细资料参阅文献[16]。

4 基本贝叶斯网络预测

应用在交通流量预测领域，贝叶斯网络的结构如图3所示。图中有两个维度：位置（横坐标）和时间（纵坐标）。假定车辆在N个路口（或路段）中行驶，图中某个结点(i,t)的拥堵状态s(i,t)依赖于t之前的若干个结点（贝叶斯网络中称其为父结点，表示为pa(i,t)），在图3中通过有向边连接到结点(i,t)的是其父结点。pa(i,t)的状态可表示为Spa(i,t)={sj,s|(j,s)∈pa(i,t)}。根据贝叶斯理论，此贝叶斯网络结点状态的联合分布可表示为：

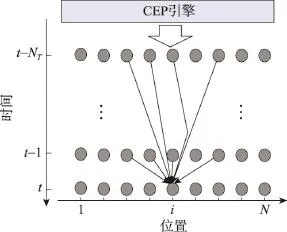
Fig.3 Bayesian network structure fortraffic flow prediction图3 用于交通流量预测的贝叶斯网络结构

其中，条件概率 p(si,t|Spa(i,t))可根据下式计算：

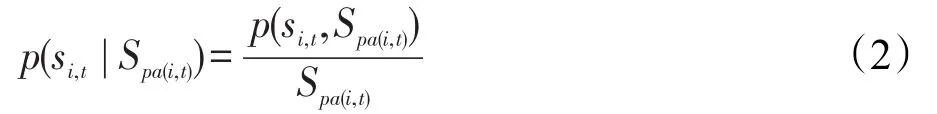
本文使用高斯混合模型[17]来近似联合分布 p(si,t, Spa(i,t))：

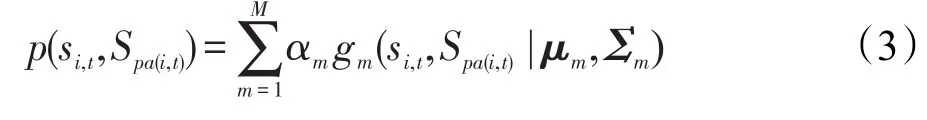
其中，M为高斯模型的数量；gm(·|μm,Σm)是第m个高斯模型的分布；μm为均值向量；Σm为协方差矩阵；αm为第m个高斯模型的系数且。采用EM算法[18]可以从样本数据中学习参数。根据获取的参数可以计算分布 p(si,t,Spa(i,t))，从而计算p(si,t|Spa(i,t))。

为了学习贝叶斯网络的结构，本文采用搜索-打分的方法，思想是最大化打分函数，从而实现贝叶斯网络结构和样本数据的最优拟合。采用的BIC（Bayesian information criterion）[19]打分函数为：

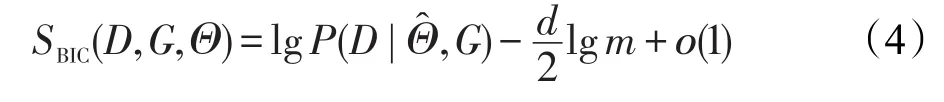
其中，D为样本数据集；G为贝叶斯网络结构；Θˆ为D的极大似然分布参数；d为边的数量；m为样本大小。学习过程分为扩张和收缩两个阶段。在扩张阶段，所有能够最大化打分函数增长的边被加入网络结构。在收缩阶段，对于那些移去以后不导致打分函数值下降的边从网络结构上移除。

5 变结构动态贝叶斯网络预测

定义4（变结构动态贝叶斯网络）变结构动态贝叶斯网络表示为，其中G(t)和Θ(t)分别表示t时刻贝叶斯网络的结构和参数，Ce(t)∊CE为t时刻的上下文类别，CE为上下文类别的集合，F为G(t)和Θ(t)到Ce(t)的映射。

尽管已经有一些动态和变结构贝叶斯网络学习和推理的研究[17,20]，但是这些方法过于复杂而难以应用到较大规模的交通流量预测中。前期的实验结果表明[21]，在交通预测领域不同的环境对应不同的贝叶斯模型。本文提出了一种基于复杂事件上下文来近似处理SVDBN的方法。由于在贝叶斯网络中结点的当前状态和一段时间内的历史状态相关，按照一个时间跨度参数δ对事件流进行划分，划分出来的每一段称为一个切片。根据事件上下文对切片数据进行聚类，并针对聚类结果的每一聚簇学习其贝叶斯网络的结构和参数。

对历史数据的聚类，本文采用减法聚类方法[22]。在聚类时使用样本数据作为候选的中心点（聚簇中心），而不是采用虚拟的中心点。对于每个数据点，基于以下公式计算其潜在值（密度）：

其中，pi(zi)为数据点zi的潜在值；N为数据点的总数；ra是一个正的常量。其原理是把某个数据点的潜在值定义为其到所有其他数据点距离的函数。选择具有最高潜在值的数据点作为第一个类的中心。然后每个数据点的潜在值都减去一个正比于其到数据中心距离的值。选择剩余潜在值最大的数据点作为下一个聚簇的中心点，以此类推。

此聚类方法的关键是计算样本之间的距离，也就是事件切片之间的距离。本文基于事件上下文来计算样本间的距离。先考虑单个上下文属性间的距离。表示事件上下文的模糊本体是一个层次化的结构。两个事件属性结点ni和nj间的距离定义如下：

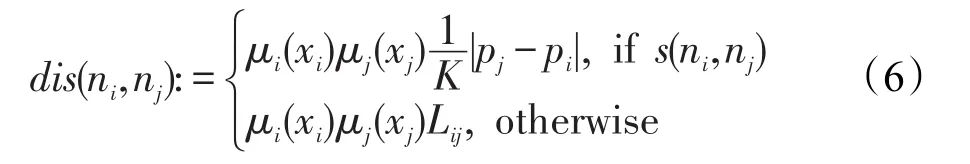
其中，μi()为结点ni上的模糊集隶属函数；s(ni,nj)表示结点ni和nj在同一个进行了模糊划分的结点上（如划分为“慢”、“中”、“快”）；K表示结点上模糊划分的数量；pi表示上下文属性对应的结点ni上模糊划分的序号（如“中”对应的序号为2）；Lij表示模糊本体层次结构上结点ni和nj之间的路径长度。

由于一个事件可能有多个上下文，为了定义上下文集合间的距离，把事件a和b对应的上下文集合分别表示为Ca=(ca1,ca2…,cam)和Cb=(cb1,cb2,…,cbn)。对于每个cai∊Ca，查找cbj满足mincbj(dis(cai,cbj))，则定义Ca到Cb的距离为：

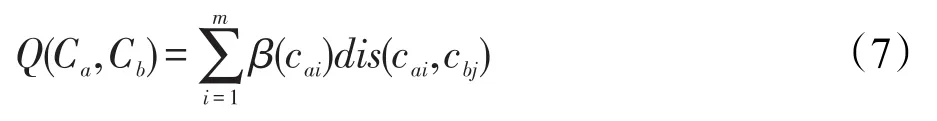
其中，函数β为距离的权重。同样定义Cb到Ca的距离为：

最终Ca和Cb之间的距离为：

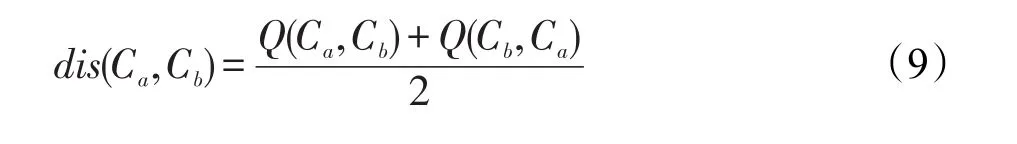
对于切片间距离的计算，把切片看作事件的集合，也采用上述方法计算集合间的距离。在确定了聚簇的中心点以后，其他样本点划分到其附近的聚簇。由于事件上下文的复杂性，允许在划分聚簇时把样本点划入多个聚簇，也就是找到k个距离最近的中心点，然后把样本划分到相关的聚簇。为了使样本在聚簇间的分布更为合理，以便贝叶斯网络的学习，对于划分到多个聚簇中的样本，基于如下图书馆准则进行划分的调整。

图书馆准则1（紧凑性）同一本书可以放在不同的书架上，但放置的方法要满足图书数量需求最小的原则。

图书馆准则2（均匀性）图书应该尽量均匀地分布在多个书架上。

对于紧凑性，首先基于式（10）计算事件上下文cei属于聚簇Ch的概率分布：

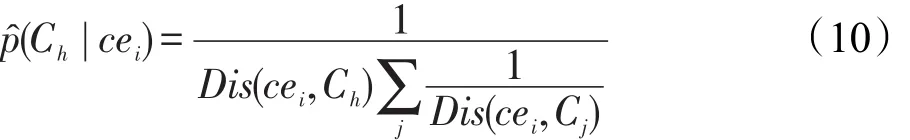
假设在初始划分时cei被划分到了k个聚簇，计算归一化熵如下：

根据紧凑性的原则，归一化熵Hnorm(cei)应该越接近0越好。在实现时对每个cei加总Hnorm(cei)的值，然后找到使其最小的划分。

对于均匀性，根据贝叶斯理论计算p(cei|Ch)：

设p(cei)=1/N，则：

则p(Ch)可按下式计算：

最终归一化熵定义为：

对于每个划分，对所有Hnorm(Ch)计算平均值，平均值越大的划分越合理。

上述方法为离线数据的聚类。在面向数据流的预测中，为了保持时效性，对离线聚类方法进行扩展以支持在线聚类。把潜在值定义为：

其中，pk(zk)为时刻k的数据点zk的潜在值。当数据增加时，可以一直使用上述公式更新潜在值，然后进行聚簇的更新。在线聚类并不从头开始运行，直接使用离线聚类中已经获得的中心点和聚簇划分，根据新的数据进行更新。

如果在线聚类产生了新的类，并且新类的样本达到一定规模，则学习新类对应的贝叶斯网络结构并应用到实时预测中。在实时预测时，如果当前上下文和已有多个聚簇的聚类比较接近（其差异小于某个阈值δ），并不选择其中聚类最小的聚簇来匹配模型，而是选择所有符合条件的聚簇，把对应的模型通过贝叶斯组合方法（Bayesian combination method，BCM）[9]进行模型组合来预测。

为了对贝叶斯网络的结构进行实时更新，假设聚簇中新增加的样本为DΔ。根据DΔ的来源确定可能受影响的结点集合VΔ和边集合EΔ。对于VΔ中的所有结点，逐个连接其所有候选父结点，如果新边的加入最大化了BIC打分函数值，则保留新加入的边，并将其合并入集合EΔ。然后对EΔ中的所有边进行判断，如果去除该边后BIC打分函数值并不下降，则去除该边。

在使用EM算法进行高斯混合模型的参数学习时，在内存中保留参数的最终值和各中间结果。为了对高斯混合模型的参数进行更新，使用当前的αm、μm、Σm参数，针对变化后的样本计算隐藏变量的分布，然后基于隐藏变量的分布根据极大似然法计算新的αm、μm、Σm参数。如果参数无明显变化或对数似然收敛，则无需更新在线参数。否则反复重复上述步骤直至收敛，并更新在线模型的参数。

6 实验研究

实验系统的结构如图4所示。系统采用Apache Kafka作为数据总线。使用了两类实验数据：真实数据和交通仿真系统产生的数据。真实数据来源于PEMS交通监测系统（https://pems.eecs.berkeley.edu/），监测的是洛杉矶市101号高速公路的数据。数据以文件的形式存储，系统运行时通过一个播放器把文件中的数据发送到Kafka系统中。交通仿真系统采用了开源项目SUMO[23]。SUMO中支持“感应线圈”获取流量数据，也可以获取每个车辆的实时位置信息（模拟为GPS）。同时扩展SUMO系统以支持其他类型的传感器，如温度、湿度、风力等。基于SUMO提供的TraCI（traffic control interface）调用接口，本实验系统实现了从SUMO中实时获取传感器的数据，并发送到Kafka形成原始事件流。

仿真系统中设置了15×15交叉路口的路网，每条路双向4车道。总共投放80万辆车，车辆的投放模拟了周五和周六两天的车流量情况，仿真系统一分钟代表实际时间的一小时。为了使仿真更接近真实的系统，制定了一些规则。公交车在固定的路线上行驶，为每辆私家车设置一个家位置和一个办公室位置。车辆以一定的概率在家和办公室之间行驶，同时以某个小的概率到其他地方，如医院或超市。在运行交通仿真时，控制系统上下文按时间段发生变化。实验使用了3台配置至强E3和16 GB内存的服务器，一台用于运行交通仿真和播放PEMS数据，一台用于实时交通流量预测，另外一台用于实时模型学习和更新。

实验中选择常规的贝叶斯网络方法[6]和深度信念网络方法[4]作为对比方法。对算法的衡量基于平均绝对百分比误差（mean absolute percentage error，MAPE），其计算方法如下：

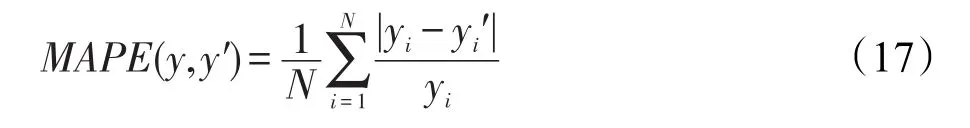
其中，yi为实际数据值；yi′为预测值。而平均准确度（mean accuracy，MA）可以用1-MAPE来计算。

实验中发现聚类的粒度和GMM中的模型数M对结果有一定的影响。粒度过小会造成每个聚簇的样本数不足，影响学习效果，同时也容易出现过拟合的问题。粒度太大则不能充分体现SVDBN的优势。在系统实现时通过多个不同粒度的聚类实验对结果进行验证，选择了最好的粒度参数进行后继的实验。在进行减法聚类时，每个数据点的潜在值都减去一个正比于其到数据中心距离的值，通过调整这个值可以调整聚类的粒度。GMM中的模型数M的选取也面临类似的情况。通过实验确定M的取值在25～30之间效果比较好。

对于PEMS数据，分别以15 min、30 min、45 min、60 min为间隔，采用3种方法进行预测。对于SUMO仿真数据，首先多次运行系统，尽量使系统出现各种类型的上下文，保存历史数据并离线训练模型。在线预测时分别以1 min、2 min、3 min、4 min为间隔进行预测。3种方法的预测流量值与实际值的对照曲线如图5和图6所示。从这两个图中能够看到实际数据的走势以及不同预测方法的大致拟合程度。

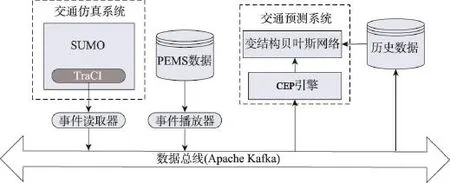
Fig.4 System implementation framework图4 系统实现框架

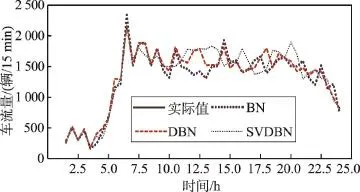
Fig.5 Prediction flow for PEMS data图5PEMS数据的预测流量

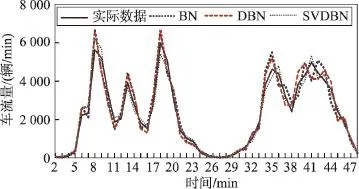
Fig.6 Prediction flow for simulated data图6 仿真数据的预测流量

3种方法在PEMS数据上进行预测时，不同时间点上的误差如图7所示。从图7中可以看出，总体上DBN的误差略低于BN，而SVDBN的误差是最小的。原因是SVDBN能够更好地适应数据的变化。此处最重要的上下文变化是“畅通”和“拥堵”间的变化。开始阶段各种方法的误差都比较大，原因是起始阶段车辆比较少，分布比较稀疏，历史状态也比较少，不利于做出预测。

3种方法在SUMO仿真系统上的误差百分比如图8所示。可以看出，和PEMS的数据相比，总体上3种方法的误差都有所增大。原因是SUMO仿真系统的数据有更多的上下文变化，从而加大了预测的难度。同时可以看出，SVDBN和其他两种方法的误差进一步拉开了差距，体现出更明显的优势。原因是SVDBN的适应变化能力更好地体现出来。

Fig.7 Error of 3 methods on PEMS data图7 PEMS数据上3种方法的误差

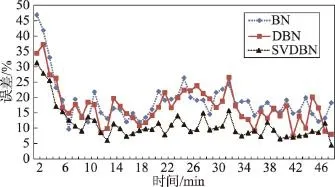
Fig.8 Error of 3 methods on simulated data图8 仿真数据上3种方法的误差

3种方法针对不同时间间隔进行预测的平均准确度对比情况如图9所示。图中可以明确体现出，无论在PEMS数据还是在SUMO仿真数据上，SVDBN的平均准确度均明显高于BN和DBN两种方法。DBN的平均准确度略高于BN，但并无明显差异。当预测时间间隔加大时，每种方法的平均准确度都下降。原因是时间间隔加长会增加更多的未观测数据，从而难以实现准确预测。

综上所述，SVDBN在预测中取得了比常用方法更好的准确度。当数据结构随时间变化得比较频繁和剧烈时，SVDBN的优越性能够更好地体现出来。

7 结论与下一步工作

Fig.9 Accuracy of 3 methods for different time spans图9 3种方法预测不同时间范围时的准确度

本文提出了一种基于变结构动态贝叶斯网络的交通流量预测方法。该方法在复杂事件处理技术的基础上，通过上下文聚类进行训练数据的划分，针对不同的聚簇训练对应的贝叶斯网络模型和参数。通过在线聚类方法支持聚簇面向数据流的实时更新，从而进一步支持模型和参数的更新。基本的贝叶斯网络结构通过BIC搜索打分的方式学习。贝叶斯网络的推理通过高斯混合模型进行近似计算。在线预测时，通过把当前上下文和已有聚簇进行匹配来选择一个或多个合适的贝叶斯网络模型。在实际数据和仿真数据上的实验结果表明，本文方法的预测准确度超过了当前常用的交通流量预测方法，并且当数据结构随时间变化得比较频繁和剧烈时，其优越性能够更好地体现出来。

本文还有一些不足之处：首先，上下文聚类的粒度和高斯混合模型中模型数量的确定，尚需要多次实验探索，缺乏一种有效的手段进行自动学习。其次，对于大规模分布式数据流下的高性能并行与分布式预测处理，还没有考虑。下一步研究将重点解决这些问题。

[1]Luckham D.Event processing for business:organizing the real-time enterprise[M].Hoboken,USA:John Wiley&Sons, 2011.

[2]Weichiang H,Dong Yucheng,Zheng Feifeng,et al.Forecasting urban traffic flow by SVR with continuous ACO[J].Applied Mathematical Modelling,2011,35(3):1282-1291.

[3]Yang Yanni,Lu Huapu.Short-term traffic flow combined forecasting model based on SVM[C]//Proceedings of the 2010 International Conference on Computational and Information Sciences,Chengdu,China,Dec 17-19,2010.Piscataway,USA:IEEE,2010:262-265.

[4]Huang Wenhao,Song Guojie,Hong Haikun,et al.Deep architecture for traffic flow prediction-deep belief networks with multitask learning[J].IEEE Transactions on Intelligent Transportation Systems,2014,15(5):2191-2201.

[5]Lv Yisheng,Duan Yanjie,Kang Wenwen,et al.Traffic flow prediction with big data:a deep learning approach[J].IEEE Transactions on Intelligent Transportation Systems,2015, 16(2):865-873.

[6]Sun Shiliang,Zhang Changshui,Yu Guoqiang.A Bayesian network approach to traffic flow forecasting[J].IEEE Transactions on Intelligent Transportation Systems,2006,7(1): 124-132.

[7]Castilloa E,Menéndezb J,Sánchez-Cambronerob S.Predicting traffic flow using Bayesian networks[J].Transportation Research:Part B Methodological,2008,42(5):482-509.

[8]Zhu Senlai,Chen Lin,Chu Zhaoming.Bayesian network model for traffic flow estimation using prior link flows[J]. Journal of Southeast University,2013,29(3):322-327.

[9]Wang Jian,Deng Wei,Guo Yuntao.New Bayesian combination method for short-term traffic flow forecasting[J].Transportation Research:Part C Emerging Technologies,2014, 43(1):79-94.

[10]Etzion O,Niblett P.Event processing in action[M].Greenwich,USA:Manning Publications Co,2010.

[11]Zhang Huawei,Chen Kerui.Building social relationship ontology model based on fuzzy sets[J].International Journal of Digital Content Technology&Its Applications,2012,6 (15):459-466.

[12]Cai Yi,Yeung C A,Leung H.Fuzzy computional ontologies in contexts[M].Beijing:Higher Education Press,2012.

[13]Fülöp L J,Árpád B,Tóth G,et al.Predictive complex event processing—a conceptual framework for combining complex event processing and predictive analytics[C]//Proceedings of the 5th Balkan Conference in Informatics,Novi Sad,Serbia,Sep 16-20,2012.New York:ACM,2012:26-31.

[14]Eleni I V,Matthew G K,John C G.Short-term traffic forecasting:where we are and where we're going[J].Transportation Research Part C:Emerging Technologies,2014,43(1): 3-19.

[15]Wang Yongheng,Cao Kening,Zhang Xiaoming.Complex event processing over distributed probabilistic event streams [J].Computers and Mathematics with Applications,2013, 66(10):1808-1821.

[16]Cao Kening,Wang Yongheng,Li Renfa,et al.A distributed context-aware complex event processing method for Internet of things[J].Journal of Computer Research and Development,2013,50(6):1163-1176.

[17]Wang Zhaowen,Kuruoğlu E E,Yang Xiaokang,et al.Time varying dynamic Bayesian network for nonstationary events modeling and online inference[J].IEEE Transactions on Signal Processing,2011,59(4):1553-1568.

[18]Verbeek J J,Vlassis N,Krose B.Efficient greedy learning of Gaussian mixture models[J].Neural Computation,2003, 15(2):469-485.

[19]Samaranayake S,Blandin S,Bayen A.Learning the dependency structure of highway networks for traffic forecast[C]// Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference,Orlando,USA, Dec 12-15,2011.Piscataway,USA:IEEE，2011:5983-5988.

[20]Shi Jianguo,Gao Xiaoguang.To speed up the inference for the structure varied discreat dynamic Bayesian networks[J]. Fire Control&Command Control,2012,37(9):71-74.

[21]Pascale,Nicoli M.Adaptive Bayesian network for traffic flow prediction[C]//Proceedings of the 2011 Statistical Signal Processing Workshop,Nice,France,Jun 28-30,2011. Piscataway,USA:IEEE,2011:177-180.

[22]Chiu S L.Fuzzy model identification based on cluster estimation[J].Journal of Intelligent&Fuzzy Systems:Applications in Engineering and Technology,1994,2(3):267-278.

[23]Behrisch M,Bieker L,Erdmann J,et al.SUMO-simulation of urban mobility:an overview[C]//Proceedings of the 3rd International Conference on Advances in System Simulation,Barcelona,Spain,Oct 23-29，2011.Wilmington,USA: IARIAXPS Press,2011:63-68.

附中文参考文献：

[16]曹科宁,王永恒,李仁发,等.面向物联网的分布式上下文敏感复杂事件处理方法[J].计算机研究与发展,2013,50(6): 1163-1176.

[20]史建国,高晓光.变结构离散动态贝叶斯网络的快速推理算法[J].火力与指挥控制,2012,37(9):71-74.

WANG Yongheng was born in 1973.He received the Ph.D.degree in computer science and technology from National University of Defense Technology in 2006.Now he is an associate professor at Hunan University,and the member of CCF.His research interests include big data,stream processing and artificial intelligence.

王永恒（1973—），男，河北霸州人，2006年于国防科学技术大学计算机科学与技术专业获得博士学位，现为湖南大学信息科学与工程学院副教授，CCF会员，主要研究领域为大数据，数据流处理，人工智能。

GAO Hui was born in 1993.She is an M.S.candidate at Hunan University.Her research interests include data mining and stream processing.

高慧（1993—），女，湖南张家界人，湖南大学信息科学与工程学院硕士研究生，主要研究领域为数据挖掘，数据流处理。

CHEN Xuanling was born in 1991.She is an M.S.candidate at Hunan University.Her research interests include data mining and stream processing.

陈炫伶（1991—），女，山西运城人，湖南大学信息科学与工程学院硕士研究生，主要研究领域为数据挖掘，数据流处理。

Traffic Prediction Method Using Structure Varying Dynamic Bayesian Networks*

WANG Yongheng+,GAO Hui,CHEN Xuanling
College of Information Science and Engineering,Hunan University,Changsha 410082,China
+Corresponding author:E-mail:wyh@hnu.edu.cn

The rapid development of Internet of things(IoT)and in-stream big data processing technology brings new opportunity to intelligent transportation system(ITS).Traffic flow prediction is the key issue of ITS.In traffic flow prediction,one fixed model cannot get excellent performance under different environments.Predicting models should also be updated according to data stream.In order to resolve these problems,this paper proposes a traffic prediction method based on structure varying dynamic Bayesian network.Based on complex event processing,this method uses context clustering to partition historical data and uses online clustering to support the update of clusters.A search-score method is used to learn the structure of Bayesian network and Gaussian mixture model is used for approximate inference of Bayesian network.When predicting at run time,appropriate model or model composition are selected based on current context.The experiments on both real and simulation data show that the proposed method has better performance than popular methods currently used.

intelligent transportation system;traffic flow prediction;complex event processing;structure varying dynamic Bayesian network

10.3778/j.issn.1673-9418.1608043

A

TP391

*The National Natural Science Foundation of China under Grant No.61371116(国家自然科学基金).

Received 2016-07,Accepted 2016-09.

CNKI网络优先出版:2016-09-08,http://www.cnki.net/kcms/detail/11.5602.TP.20160908.1047.024.html

WANG Yongheng,GAO Hui,CHEN Xuanling.Traffic prediction method using structure varying dynamic Bayesian networks.Journal of Frontiers of Computer Science and Technology,2017,11(4)：528-538.