Biot方程的完备通解在一维情况下的验证
颜凝香 吴利华 范克
(1.江苏省水利工程科技咨询股份有限公司南京2100292.南京市水利规划设计院股份有限公司南京210022)
Biot方程的完备通解在一维情况下的验证
颜凝香1吴利华2范克2
(1.江苏省水利工程科技咨询股份有限公司南京2100292.南京市水利规划设计院股份有限公司南京210022)
基于三维饱和弹性土体Biot方程的完备通解,构造了一维情况下的一组中间变量,这些变量是坐标和时间的函数,进而得到一维情况下位移和孔压的解析解表达形式。通过给出一维算例的边界条件求出中间变量表达式中的系数,得出位移和孔压的最终表达式,即Biot方程的一维解答。
饱和土Biot固结完备通解理论解
1 引言
Biot(1941)在从严格的固结机理出发推导出能准确反映孔压消散与土骨架变形相互关系的三维固结方程,具有重要的理论及工程应用价值。但是Biot固结方程是一组偏微分方程,在数学上求解非常困难,对于轴对称问题和一些简单的平面应变问题,有人推出了解析解;对于一般复杂边界的土层情况,便无法求得解析解。河海大学王媛教授给出了三维Biot饱和土理论的完备通解。本文在直角坐标系下分别应用该通解和太沙基理论来解答土体单向固结的算例。以验证Biot方程通解表达的实用性。Biot理论和太沙基理论的假定是基本一致的,即符合骨架线性弹性、变形微小,渗流符合达西定律等,所不同的是太沙基理论增加了土体在固结过程中法向总应力和不随时间而变的假定,对于一维固结问题,则不存在这个问题,此时的太沙基方程和Biot固结方程是一致的。
2 通解中参数的构造
三维Biot饱和土理论的方程组为:

式中:u为位移,p表示孔压,k和γw分别为土体渗透系数和水的重度。
方程组(1)有如下通解:

由于(2)是(1)的完备解,因此求解Biot边值问题转变成求出满足方程(3)的h、,使其满足(2)就可以了。
一维情况下,构造满足(3)式的h,可表达为:
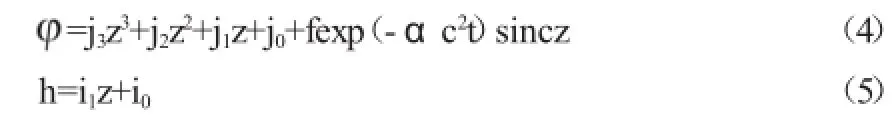
式(2)在一维情况下可写为:
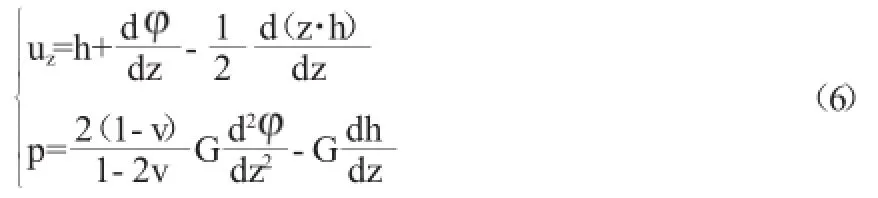
将式(4)、式(5)代入(6)得

3 Biot理论一维算例解答
图1为均质、各向同性的饱和粘土层,位于不透水的岩层上、粘土层的厚度为H,在自重应力作用下已固结稳定,仅考虑外加荷载引起的固结。若在水平地面上施加连续均布压力,则在土层内部引起的竖向附加应力沿高度的分布将是均匀的,且等于外加均布压力,即σz=p0。
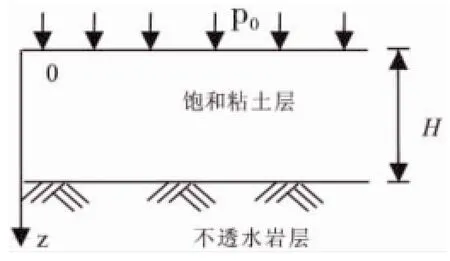
图1 饱和粘土的一维固结图
则有空隙水应力初始条件和边界条件如下:
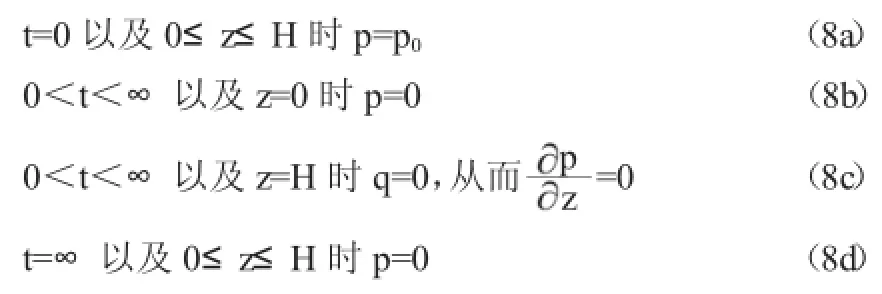
位移初始条件和边界条件:

另外,根据有效应力原理,有以下应力条件:

将以上式(8c)(8d)(9b)(9c)可求得

记Cn=fc,则上式中位移表达式写为以下通式:


只有当n'=n时,上式左边不为0。则有

将上式代入式(10)得

则孔压可表达为:

4 太沙基解答
太沙基一维固结微分方程式:

式中,Cv为固结系数。
分离变量,假定p可以表示为:

代入微分方程(14)得

方程两边为不同变量的函数,只有当它们都等于常量时才有可能,令这个常量为-B2。
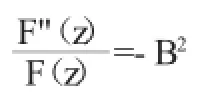
可解得F(z)=A1cosBz+A2sinBz
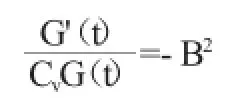
解得G(t)=A3exp(-B2Cvt)
将它们代入式(14)得

利用透水面边界(8b)得A1=0。上式第一项消去,即

利用不透水边界条件(8c)对上式求解:

代入式(16)并写成通式:

利用初始应力条件(8a)得
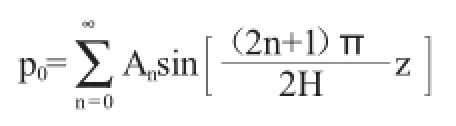

只有当n'=n时,上式左边不为0,得

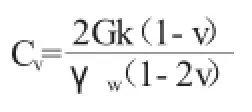

将上式代入式(19)得

可见式(20)与Biot方程的解即式(13)是相同的。
5 结论
本文构造了直角坐标系下符合三维Biot饱和土理论通解的参量,并以此为依据得到一维固结情况下的详细解答,同时以太沙基理论求解同一算例,结果证明两种解答在一维情况下是一致的。验证了Biot方程完备通解的实用性。此外,基于Biot固结理论完备通解在二维和三维情况下的应用正在研究中■

