矿井气候多参数预测与通风网络自动解算算法研究*
马 恒,高 巍,周西华
(1. 辽宁工程技术大学 安全科学与工程学院,辽宁 阜新 123000; 2. 矿山热动力灾害与防治教育部重点实验室,辽宁 阜新 123000)
0 引言
自通风网络解算方法被提出以来,通过国内外学者不断研究,该领域的技术日渐成熟,开发出大量的矿井通风网络仿真软件。但许多软件对矿井气候的考虑仍停留在静态的层次上,即需要人事先测量出各网络节点矿井气候参数,然后再得出自然风压。过程繁琐耗时长,工作量大。如何进行快速、简单且不失准确的计算是目前需要解决的问题。本文通过对风流的压强和温度变化规律的研究,在已知进风口风流温度和压强情况下,预测巷道各点风流温度、压强,进一步得出各巷道平均密度,得出矿井含自然风压的通风网络动态解算算法,并基于MATLAB软件对算法进行程序设计,对算法进行验证。
1 井巷风流密度计算
1.1 风流平均密度
井巷风流密度是影响自然风压的一个重要参数。气体的可压缩性会对风流的密度造成变化,这个变化约为6%~8%[1]。由于影响较小,在一般情况下,将矿内风流视为非压缩性流体来对待,即近似视为等容过程。由此平均密度计算公式[2]:
(1)
式中:p1,p2分别为始末节点空气的压强,Pa;ρ1,ρ2分别为始末节点空气的密度,kg/m3;ρm为平均密度,kg/m3。
由公式可知,当空气被设为不可压缩流体时,密度的变化主要由压强来决定。上述平均密度计算公式过于繁琐,对于平均密度的计算,可以用两端点的算术平均值[3]:ρm=(ρ1+ρ2)/2来代替,满足计算要求。
1.2 风流密度计算
计算井下湿空气密度[4]:
ρ=0.003 48(P-0.377 9φPs)/T
(2)
式中:P为湿空气的压强,Pa;T为湿空气的绝对温度,K;φ为湿空气的相对湿度,%;Ps为饱和水蒸气分压力,Pa。
由公式可知,φ由测量的干湿温度得来,Ps可根据T查表得出,因此,只要知道矿井巷道各点风流的温度T和压强P就可得出各个分支节点密度。这通常需要实地测量湿空气压力P,干球温度td和湿球温度tw才能得出。
2 矿井气候多参数预测下的自然风压算法的实现
现有自然风压的计算均是通过实地测量湿空气压力,干球温度和湿球温度来进行的[5],由于测点与数据较多,其过程不但繁琐还无法达到动态计算的目的。对此,笔者考虑在已知井口大气压强p0和干湿温度t0d和t0w的情况下,预测出井下各个节点的压强和温度,再通过各个节点的压强和温度能得出各个节点的风流密度。因此需要引入各节点风流温度和各节点压强计算公式。
2.1 风流温度的计算
(1)井筒风流温度的计算方程为[6]:
(σ-g/CPL)Qρ0 sCPL/λtK(α)
(3)
式中:T0m为井底(井筒末端)温度,K;T0 s为地面(井筒始端)温度,K;σ为地温梯度,不同地区地温梯度不同;Z为井筒始末两端高差,m;L为巷道长度,m;λ为导热系数,W/(m·K)。根据文献[6]查表得出;K(α)为不稳定换热系数,通过毕欧准数和傅立叶准数查表得出;Q为风流体积流量,m3/s;ρ0s为巷道入口的风流密度,kg/m3;CPL为干空气的定压比热,一般取1 005 J/kg·K;g为重力加速度,m2/s,一般取9.81。
(2)普通巷道风流温度的计算方程为[6]:
(4)
式中:Tgu为原岩绝对温度,K;U为巷道周长,m;γ0为巷道当量半径,即巷道有效截面和积湿周之比定义为水力半径,当量半径定义为二倍的水力半径,m;根据文献[6],Δhp为由于各种热源引起的风流热焓增值,J/kg。
2.2 风温预测的准确性分析
由公式(3)和(4)可知,风温预测需考虑的参数过多,因此,保证每个节点计算的温度可靠性是有必要考虑的。首先,干空气的定压比热CPL在温度250~300 K的范围内,其数值变化在1 003~1 005之间,所以取1 005并不影响结果。其次,式中可以准确得到的参数:进风井口温度T0 s(在井口容易测),高差Z,巷道长度L,周长U,当量半径γ0。在矿井建设的过程中这些参数在图纸上都会标出,不需要再次测量。而原岩温度Tgu,地温梯度σ,导热系数λ和不稳定换热系数K(α)都与地质条件和岩石物理性质有关,因为建井前需要进行地质条件、水纹条件和岩层情况的考察,原岩温度和地温梯度都可以直接得出,而导热系数λ和不稳定换热系数K(α)需要知道巷道处在哪个岩层中,了解岩石性质,通过计算和查表也可以得出[6]。唯一不确定的参数就是风量Q和节点密度ρ0s,由于不能实测且在下文的网络解算的过程中这2个参数数值不断变化,因此会对风温预测结果造成影响,由公式(3)和(4)可知,Q*ρ可作为一个参数来考虑,以图1为例,假设其他的参数都已确定且不变,当进风口Q*ρ分别等于30,40,50时,各节点温度值。分析结果见表1。
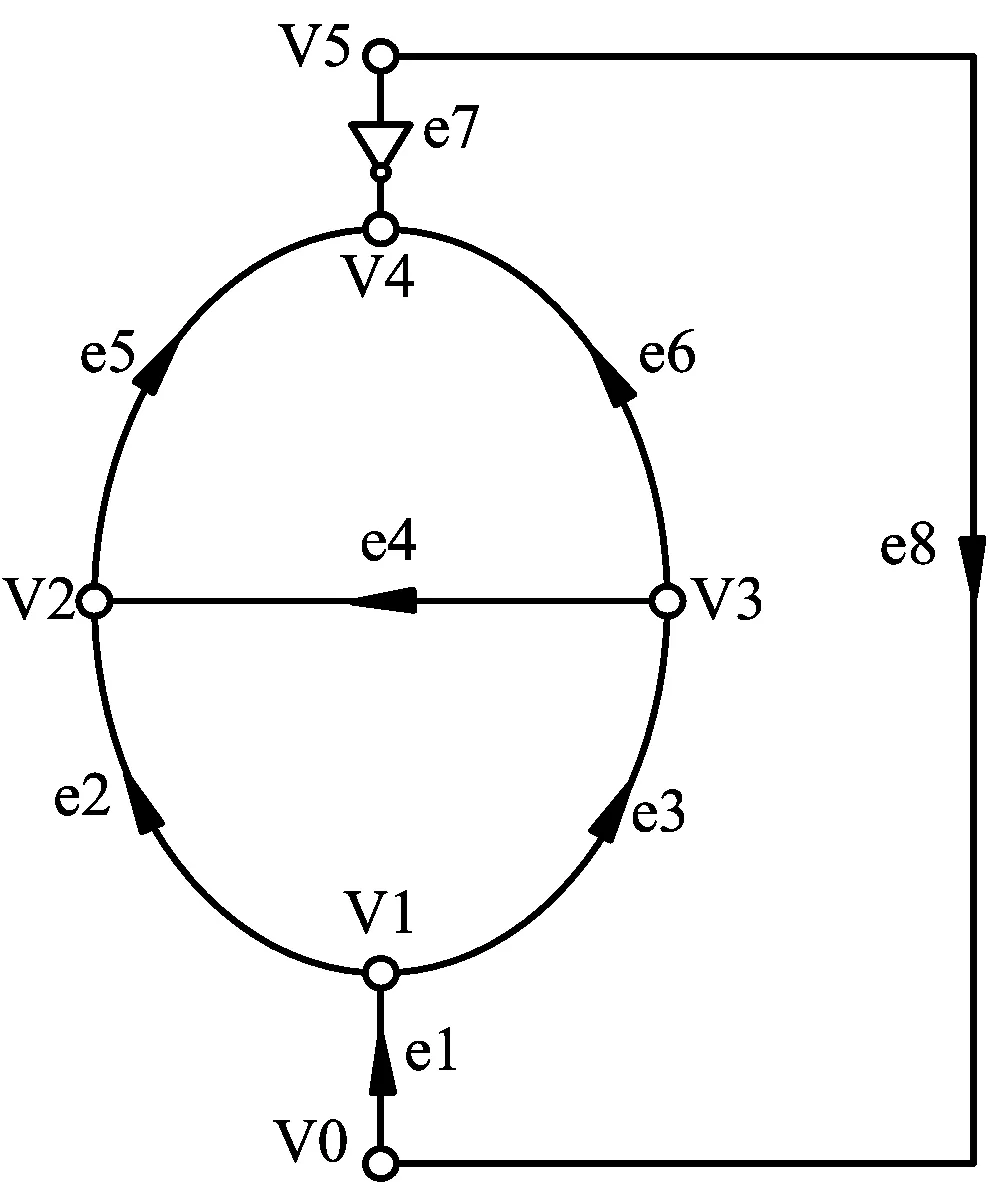
图1 矿井通风系统简Fig.1 Diagram of mine ventilation system

Q*ρT/KV1V2V3V4V530278.0141280.2022280.4145282.1756281.269840278.0144280.1572280.4067282.1422281.236650278.0145280.1296280.3975282.1202281.2146最大绝对差0.00040.07260.01700.05540.0552
结论:Q*ρ分别为30,40,50的情况下,温度变化在0.000 4~0.072 6的范围内,变化很小。因此风量Q和节点密度ρ对风温的影响很小。而真正对风温影响很大的高差,原岩温度和始点温度都能够通过各种方式准确的得到,可以保证进回风井和普通巷道的温度预测的准确性,至于拥有额外热源的特殊巷道,文献[6]、[7]介绍很清楚,主要考虑机器运作产生热量Δhp,而产热量可以根据机器的铭牌和实际运作功率等计算出。
2.3 各点压强的计算
点压强计算公式[7]:
(5)
式中:p1,p2分别为始末节点空气的压强,Pa;ρ1s,ρ1m为始末节点空气的密度,kg /m3;g为重力加速度,m2/s,一般取9.81;Q1为风流体积流量,m3/s;Z1-2为始、末节点标高差,m。
2.4 自然风压的计算
由前文可知,平均密度由ρm=(ρ1+ρ2)/2来代替。得到最终的自然风压计算公式[8]:
(6)
式中:hn为矿井自然风压,Pa;ρs,ρm为通路上各分支的始节点、末节点的密度,kg/m3;Zs-m为始、末节点标高差,m。
通过式(2)、(5)和(6)可以得出:
0.377 9φiPs)/Tis+ ((Pis+ 0.001 74(Pis-
(7)
3 通风网络实时解算与程序实现
3.1 Cross迭代算法改进
Cross法,即斯考德-恒斯雷法[9]。其运算过程:按规定选择独立回路,运用高斯迭代法逐次求解回路内的风量修正量Δqi,直到满足精度ε为止,见公式(8)和(9)。
(8)
(9)

在原有Cross迭代法的基础上,加入上文自然风压计算方法和原理[10-15],实现含有自然风压的通风网络实时解算。在运算过程中,还需考虑以下几个问题:
1)由式(7)、(8)和(9)可知,将各节点温度和压强同时进行迭代,存在迭代不收敛可能。为了避免此情况的发生,在程序编制中,对计算方法进行简化。首先在不考虑自然风压的情况下进行一次迭代计算,通过此计算得出各分支风量值,该分支风量作为计算各节点的风流温度初始参数,在之后的迭代计算中将一直使用此温度不变。
2)因为网络各节点压强和密度的计算均需已知彼此才能得出,在两者均未知情况下,为了保证计算能进行,在初次迭代时需拟定各节点密度值,即假设各节点初始密度均等于井口空气密度,这样就可以计算出各点压强,再利用得到的点压强在下次迭代中得出各节点密度,依次循环。注意这个拟定的初始密度值只在初次计算应用。
3)需考虑湿度对自然风压的影响,经验可知[4],湿度与巷道壁的潮湿度和蒸发率有关,这些变化都是复杂难测,因此,只能得出范围值,现将通风系统分为进风段、用风段、回风段3个部分来简化。相对湿度在井下变化趋势:夏季,风流的相对湿度一直增加状态,到回风段时会达到90%~100%;在冬季,风流的相对湿度刚开始会减小或不变,但到用风段与夏季变化趋势一样,到回风段时也会达到90%~100%。自然风压预测的另一个主要因素:高差,高差主要在进风井和回风井,而用风段几乎不存在高差,对自然风压的预测中影响很小。进风井的平均相对湿度应该高于进风口风流相对湿度的0%~20%。除了青藏高原与新疆部分盆地,我国其他地区空气的相对湿度都达到60%以上。因此,假如进风口处的相对湿度为60%,那么进风侧的平均相对湿度应该在60%~80%之间,回风段的相对湿度在90%~100%之间,而用风段相对湿度就应该在80%~90%之间。取中间数就是进风段:70%;用风段:85%;回风段95%。应用取范围中间数的相对湿度预测方法,可保证预测的相对湿度与真实的相对湿度误差上下不超过10%。当然,这里的预测经验主要应用于我国煤矿,煤矿绝大多数均为潮湿巷道。误差分析:例如,温度为0,5,15,20,25℃,巷道高差为100 m,压强为100 000 Pa,假设预测相对湿度为70%而实际上为60%,密度与自然风压计算误差结果见表2。
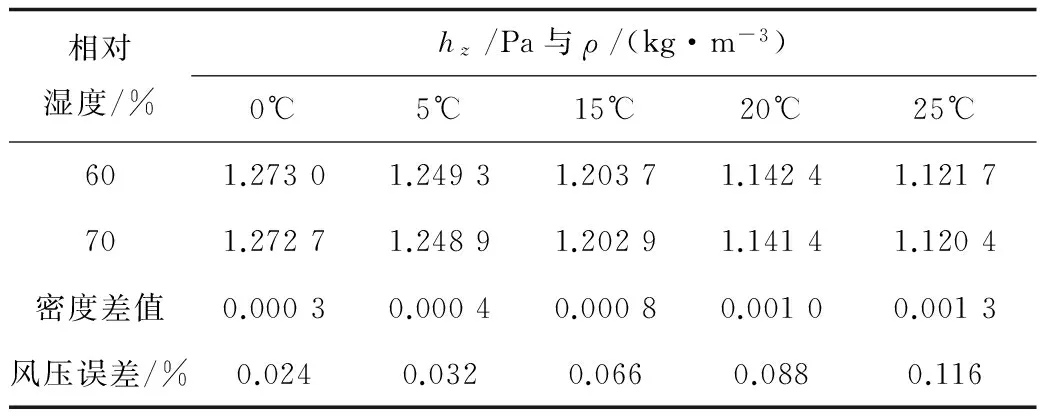
表2 计算结果对比Table 2 Comparison of results
结论:由公式2和6,矿井温度0~25℃的相对湿度每相差10%,风流密度就相差0.000 3~0.015,自然风压每一百米的高差就产生0.29~1.45 Pa的误差,自然风压误差在0.024%~0.116%,。因此采用分3段预测和取中间值的方法代替实测每个点的相对湿度,可以最大程度上减少误差,误差值对自然风压的影响在可控的范围内。受自然风压影响越大的矿井预测越准确,误差控制在1%以下。此方法为相对湿度对自然风压造成误差降到最低。
其算法程序流程为:
1)已知:G=(V,E)、总风量、分支风阻、初拟风量和各个分支始末两端节点的高差。
2)对通风网络G的分支和节点进行编号,拟定树与余树。
3)拟定基本回路矩阵:C。
4)在不考虑自然风压和通风机风压的情况下,对网络各个分支进行初步分风(其目的是为初次拟定温度和点压强提供风量)。
5)已知:井口大气压p0与大气温度T0,求得井口密度ρ0。并根据公式(3)和(4)确定网络各个节点的温度。
6)先拟定网络各节点密度ρi均为ρ0,并带入公式(5),通过公式(7)、(8)和(9)对其进行迭代运算。(考虑湿度影响)
7)检查各参与迭代的回路风量修正量Δqi,若max(|Δqi|)<ε满足精度,则进入步骤9,否则转回6。
8)k=k+1。(k为迭代次数)
9)结束迭代,输出结果
3.2 程序验证
如图2建立的一个简单矿井模型。表3为程序是否含有自然风压的2种情况下解算运行结果对比表,运算结果证明:虽然在不考虑自然风压的情况下解算结果较准确,但与考虑自然风压的情况下的结果相比还存在一定差距,因此在解算中对自然风压的考虑是有必要的。
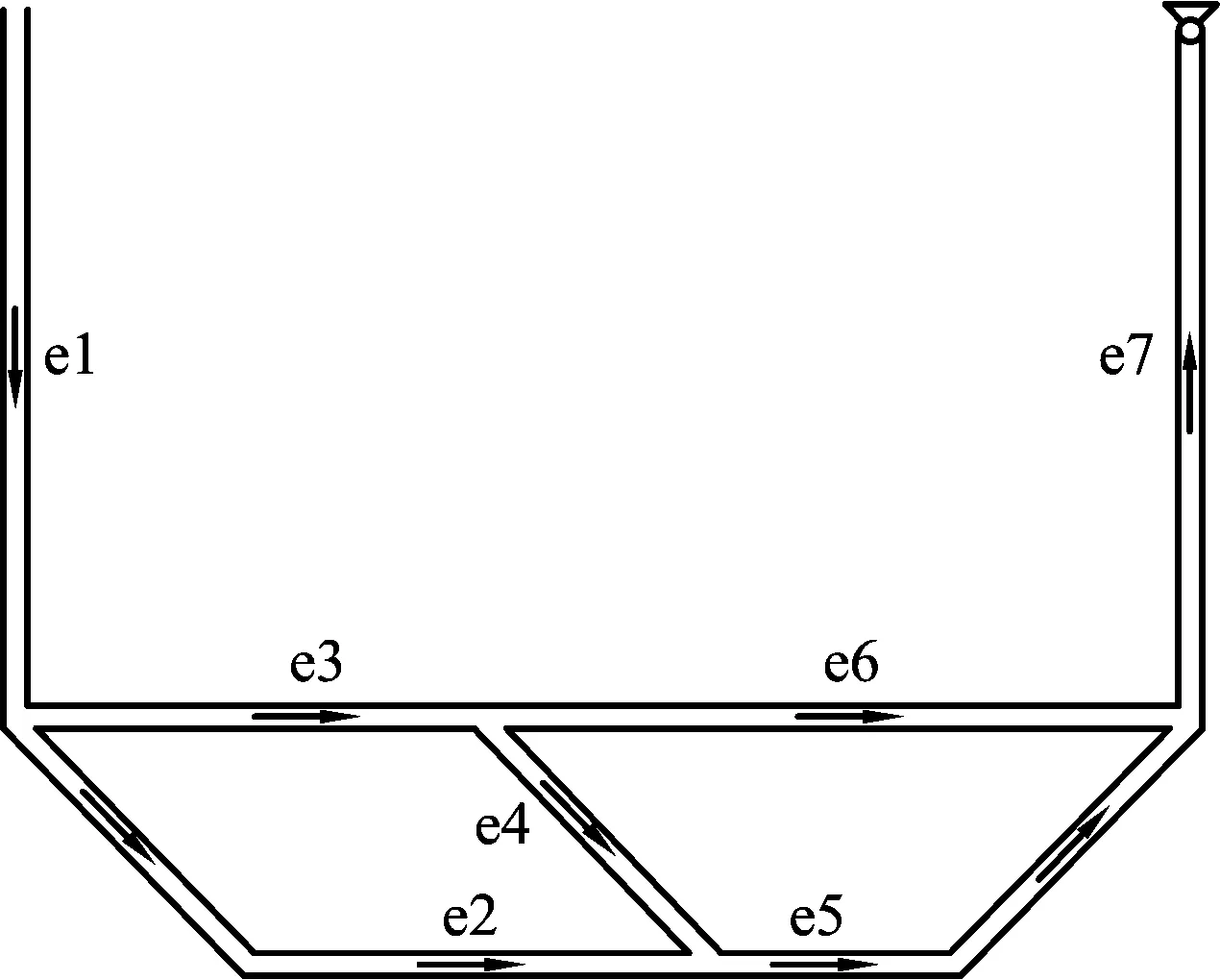
图2 简单矿井模型Fig.2 MVIS ventilation system network settlement
如图2所示,已知井口压强和温度分别为p0=100 000 Pa,T0=275 K,各分支标高差Z1=300 m,Z2=20 m,Z3=0 m,Z4=20 m ,Z5=30 m,Z6=50 m,Z7=250 m。认为所有巷道长度L=500 m,R1=R2=R3=R4=R5=0.03N·s2·m-8,R6=R7=0.06 N·s2·m-8,导热系数λ均为2 W/(m·K),周长均为15 m,当量半径γ0=3 m,设e1,e2,e3为进风段,e4为用风段,e5,e6,e7为回风段,由上文的相对湿度预估经验,节点1到节点5相对湿度φ分别为70%,85%,85%,95%,95%,Δhp1-2=Δhp1-3=Δhp3-4=Δhp2-4=2 010 J,hf=30 Pa,Q1=Q7=30 m3/s。

表3 计算结果对比Table 3 Comparison of results
计算结果见表4,5和6,由图3,4,5,6分析表明:经过7次迭代,回路风量修正量Δqi满足精度且密度、压强、自然风压和风量在运算过程中均收敛,证明本程序满足通风网络解算的设计要求,也证明了矿井气候多参数预测与通风网络解算算法的结合是可实行的。

表4 迭代验算Table 4 Iterative calculation

表5 迭代验算Table 5 Iterative calculation

表6 迭代验算Table 6 Iterative calculation

图3 各节点压强迭代数值变化曲线Fig.3 Each node pressure iteration value curve
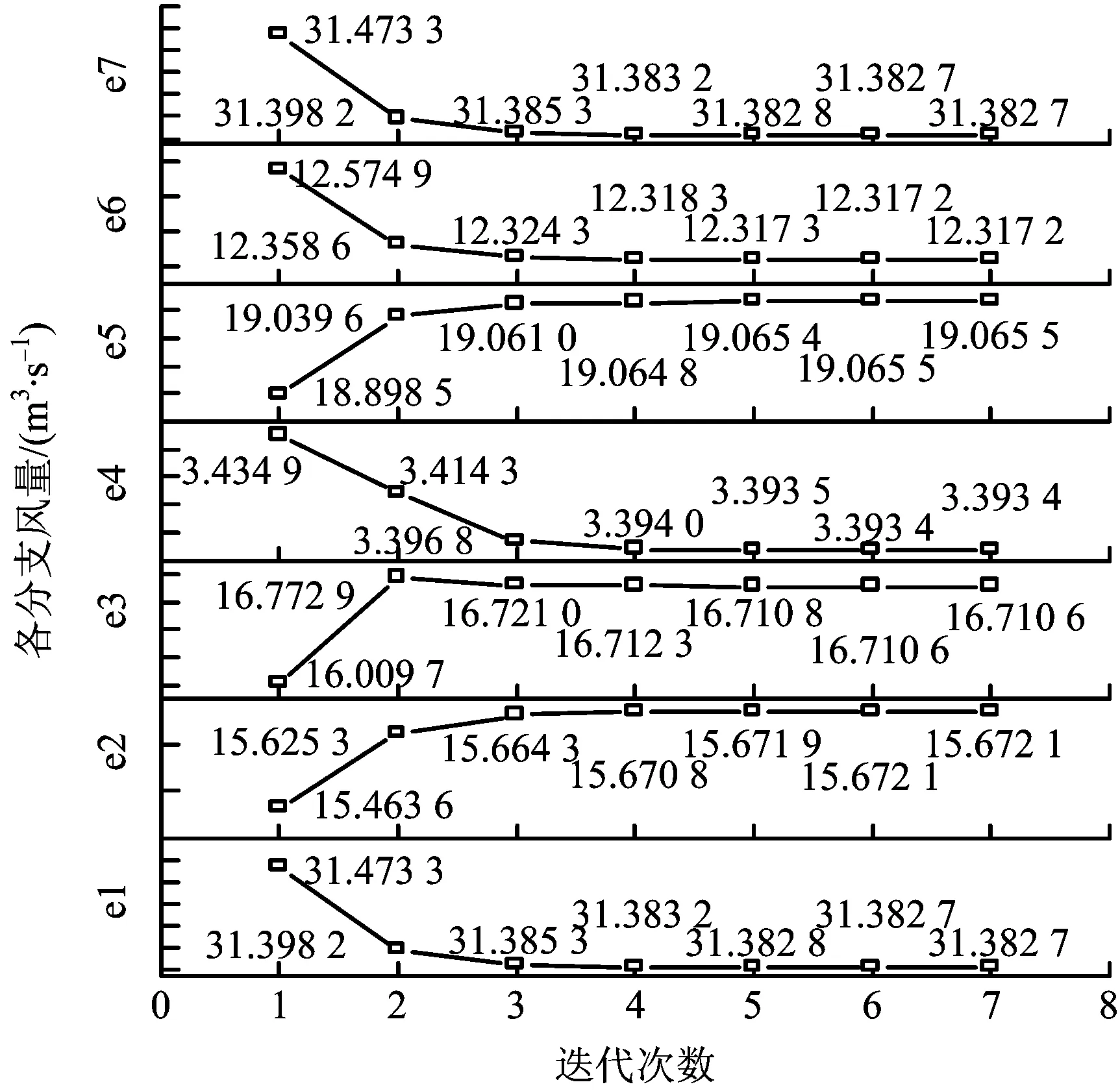
图4 各分支风量迭代数值变化曲线Fig.4 Each branch wind volume iteration curve

图5 各节点密度迭代数值变化曲线Fig.5 Each node density iteration value curve
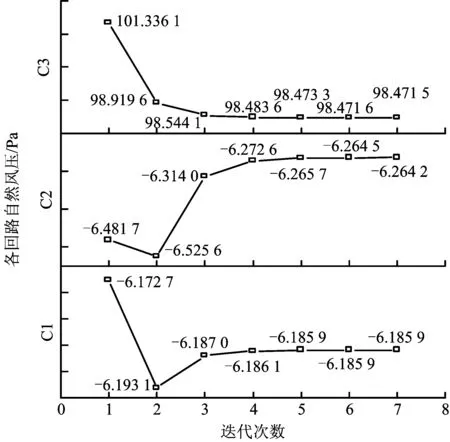
图6 各回路自然风压迭代数值变化曲线Fig.6 Natural wind pressure of each circuit volume iteration value curve
4 结论
1)通过对风流的压强和温度变化规律的研究,在已知进风井入口风流的温度和压强,预测计算出矿井巷道各节点风流的温度和压强,从而得出各个巷道平均密度,实现了快速、简单且不失准确度的计算矿井自然风压目的。
2)结合Cross网络解算方法,在已知井口初值的情况下,实现了自然风压和机械压双重作用下的复杂矿井含自然风压的通风网络自动解算的过程。
3)通过建立矿井模型对本程序进行验证,证明了在通风网络解算中对自然风压的考虑是有必要的。又经过实验验证,本程序满足通风网络解算的设计要求,也证明了矿井气候多参数预测与通风网络解算算法的结合是可实行的。
[1]王海宁. 矿井风流流动与控制[M]. 北京:冶金工业出版社, 2007.
[2]林海飞,刘静波,严敏. CO2/ CH4在煤储层中扩散规律的分子动力学模拟[J]. 中国安全生产科学技术, 2017,13(1):84-89.
LIN Haifei, LIU Jingbo, YAN Min.The molecular dynamics simulation of the diffusion of CO2/CH4in the coal reservoir[J]. Journal of Safety Science and Technology, 2017,13(1):84-89.
[3]马恒,张越,周西华. 含自然风压通风网络的自动解算及应用[J]. 金属矿山, 2016,32(1) :157-161.
MA Heng, ZHANG Yue, ZHOU Xihua,. Automatic calculation and application of ventilation network with natural wind pressure[J]. Metal Mine, 2016, 32(1) : 157-161.
[4]周西华,王继仁,洪林. 湿空气密度的快速准确测算方法[J]. 矿业安全与环保, 2005,32(4) :49-51.
ZHOU Xihua, WANG Jiren, HONG Lin. Fast accurate measurement of wet air density[J]. Mining Safety ﹠ Environmental Protection, 2005, 32(4): 49-51.
[5]王海宁,汪光鑫,刘红芳. 矿井自然风压适时计算与应用[J]. 矿业研究与开发, 2014, 34(2): 77-80 .
WANG Haining, WANG Guangxin, LIU Hongfang. Timely calculation and application of mine natural wind pressure[J]. Mining Research and Development, 2014, 34(2): 77-80.
[6]马恒,尹彬,刘剑. 矿井风流温度预测分析研究[J]. 中国安全科学学报, 2010, 20(11): 91-95.
MA Heng, YIN Bin, LIU Jian. research on prediction airflow temperature in Mine[J]. Chinese Safety Science Journal, 2010, 20(11): 91-95.
[7]约阿希姆.福斯. 矿井气候[M]. 北京:煤炭工业出版社,1989.
[8]李恕和,王义章. 矿井通风网络计算的牛顿法[J]. 煤炭学报, 1982, 10(4): 52-62.
LI Shuhe,WANG Yizhang. The Newton method for the mine ventilation network[J]. Journl of China Coal Society, 1982, 10(4): 52-62.
[9]刘剑,贾进章,郑丹. 流体网络理论[M]. 北京: 煤炭工业出版社, 2002.
[10]宫良伟,何华,邹德均. 通风网络解算中自然风压处理[J]. 矿业安全与环保, 2015, 42(6): 113-116.
GONG Liangwei,HE Hua,ZHOU Dejun.Treatment of natural wind pressure in ventilation network flowcalculation[J]. Mining Safety ﹠Environmental Protection, 2015, 42(6): 113-116.
[11]陈明生,陈伯辉,沈斐敏. 矿井通风优化评价指标体系权重确定[J]. 中国安全生产科学技术, 2011, 7(3): 22-25.
CHEN Mingsheng,CHEN Bohui, SHEN Feimin.Weight determination of evaluation index system in mine ventilation optimization[J].Journal of Safety Science and Technology, 2011, 7(3): 22-25.
[12]钟德云,王李管,毕林. 复杂矿井通风网络解算风网有效性分析[J]. 中国安全生产科学技术, 2014, 10(11): 10-14.
ZHONG Deyun, WANG Liguan, BI Lin.Analysis on ventilation network effectiveness in ventilation network calculation of complex mine[J]. Journal of Safety Science and Technology, 2014, 10(11): 10-14.
[13]邓云峰,盖文妹.基于动态网络流的区域疏散分析模型与仿真[J].中国安全生产科学技术, 2016, 12(11): 24-30.
DENG Yunfeng,GAI Wenmei.Analysis model and simulation of regional evacuation based on dynamic network flow[J].Journal of Safety Science and Technology, 2016, 12(11): 24-30.
[14]周西华,王继仁,卢国斌.回采工作面温度场分布规律的数值模拟[J]. 煤炭学报,2002,27(1): 59-63.
ZHOU Xihua,WANG Jiren,LU Guobin.The numerical simulation of distribution law of temperature field in coal face[J]. Journal of China Coal Society, 2002,27(1) :59-63.
[15]王树刚,徐哲,张腾飞.矿井热环境人体热舒适性研究[J]. 煤炭学报, 2010, 35(1): 97-100.
WANG Shugang, XU Zhe, ZHANG Tengfei. Human thermal com-fort for mine environment[J]. Journal of China Coal Society,2010, 35(1): 97-100.

