铁路专用线危险货物运输安全指标属性约简研究*

王文宪，况　瑢，郭经纬，吕红霞

(1. 河南理工大学 能源科学与工程学院， 河南 焦作 454000；2. 西南交通大学 交通运输与物流学院， 四川 成都610031)

0　引言

作为我国危险货物运输的重要组成部分，铁路危险货物运输占总运量的80%以上。截止2016年底，全路危险货物办理站数量达76个，接轨站1 300余个，办理危险货物的运输专用线超过2 000条，实现运量约1.4亿吨[1]。铁路危险货物运输到发、装卸作业主要集中在专用线办理，专用线作为铁路危险货物运输的重要作业场所，安全设备设施是否齐全，安全管理制度是否健全，从业人员专业技能是否可靠等，均会对危险货物运输的安全性造成直接影响。因此，铁路专用线危险货物运输安全评价是重要的基础工作，可实现危险货物运输风险识别的有效性与准确性，从而减少安全事故的发生。

针对铁路专用线危险货物运输安全评价方面的研究，Glickman[2]通过统计年度铁路编组站液体货物泄漏事件概率并对其危险性进行量化评估；Cozzani[3]构建了铁路编组站危险性评估理论框架；张江华[4]系统归纳总结了国内外危险化学品运输风险分析的相关研究成果及不足；其他学者王喆[5-6]、刘雪鹏[7]等，在构建专用线危货运输安全评价体系基础上，采用诸如突变理论、灰色评价模型以及模糊综合评价方法进行量化分析。以上研究的重点侧重于铁路专用站及专用线评价方法的选择，在评价指标选择中通常只分析其原则，针对评价体系构建中指标相关性、冗余性处理的研究较少。

粗糙集理论[8](RS，Rough Set)于1982年由波兰数学家的Pawlak提出，主要用于学习、表达以及归纳具有不确定性及不完整性的数据知识，在没有任何先验知识及附加信息的情况下，从知识分类角度利用数据本身自带信息对其进行推理。粗糙集理论的属性约简方法中，基于区分矩阵的属性约简算法易于理解，且具有多项式时间复杂性的优点[9]，被广泛应用于工程技术领域中与金融学领域中的数据挖掘、评价指标精简等方面。基于上述分析，本文在分析铁路专用线危险货物运输安全影响因素基础上，构建评价指标体系，采用基于改进区分矩阵的粗糙集属性约简方法，在保证知识分类质量不变的前提下，对评价体系指标进行精简，从而提高评价过程中的科学性。

1　评价体系的构建

铁路专用线危险货物运输的影响因素众多，评价体系的构建需从总体上反映专用线运输事故的本质。事故致因理论认为：造成事故的原因包括人的因素、设备因素、线路因素以及管理因素，所以从“人、机、路、管”角度出发，铁路专用线危险货物运输的影响因素也应该从资质管理C1、安全设备设施C2、运输设备设施C3以及安全管理C4这4个方面考虑[10]。

1.1　资质管理

危险货物运输托运人资质是由国家相关部门认定，从事该类运输业务单位所获得的危险货物存储、运营资格[11]。《危规》规定，从事铁路危险货物运输的托运人或单位必须具备相应的资质。资质管理包含的考核指标包括托运人的资质证书以及危险货物运输经营许可2种证书，而且需要满足危险货物的各项规定。

1.2　安全设备设施

铁路危险货物专用线的设施设备中，每一个零部件的质量与使用规范都对整条专用线的安全状况造成直接影响。安全设备设施包含的考核指标包括危险货物的消防设施、防雷设施以及防静电设施，安全检测及报警设备，应急救援物资，安全监控系统等，此外还包括设施之间的安全距离是否符合标准[12]。

1.3　运输设备设施

在危险货物的运输过程中，不同外界条件的作用都有可能导致各类危险货物事故的发生，此外，某些危险货物还会因为摩擦振动而产生化学反应并生成有毒物质。因此，运输的危险货物要与所使用的运输工具与包装相适应，危险货物载运工具及安全附件需要符合《铁路危险货物运输管理规则》要求。危险货物的运输包装应该是由取得国家规定的企业生产，由铁路总公司认定的包装检测机构检测合格。

1.4　安全管理

铁路危险货物运输过程中包含各类复杂的技术作业流程，且对安全条件要求较高，其制度管理涉及社会与环境的安全。因此，铁路危险货物专用线应根据自身的运营状况及技术条件，制定与实施各项严格的管理制度与应急预案。安全管理所包含的考核指标主要包括安全管理制度、从业人员安全培训以及应急预案等内容的规范情况等[13]。

综上，构建铁路专用线危险货物运输安全评价体系如图1所示。该体系包含有4个二级指标，以及16个三级指标。

图1　铁路专用线危险货物运输安全评价体系Fig.1　Rail line dangerous freights transport security assessment system

2　基于粗糙集理论的属性约简

2.1　改进区分矩阵设计

基于粗糙集理论的铁路专用线危险货物运输安全评价体系约简的关键在于区分矩阵设计。但由于某些不相容决策表中，区分矩阵属性约简与正域属性约简之间并不等价，因此需要对传统意义上的区分矩阵进行适应性的修正。

定义1铁路专用线危险货物运输安全评价决策表S=(U,A,V,F)，论域U={u1,u2,…,un}为铁路专用线危货运输统计数据及评价结果组成的样本集；A=C∪D为有限属性集，其中子集C为条件属性集，为评价体系中的各个三级指标，子集D为决策属性集，反映铁路专用线危险货物运输二级指标安全等级评价类别，且C与D满足C∩D=φ；V=(Ua∈A,Va)为属性取值的集合，其中Va是属性a的值域，也就是属性a的取值范围；F:U×A→V为信息函数，用于确定论域U中每个样本u关于属性a的信息值，且∀a∈A,x∈U，F(u,a)∈Va。

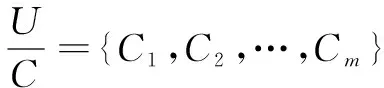
(1)

(2)

定义4在简化决策表S′=(U′,C,D,V,F)中，简化区分矩阵为M′=m(i′,j′)，矩阵中包含的元素定义如下[14]：

(3)

定义5假设M′=m(i′,j′)为简化决策表S′=(U′,C,D,V,F)的简化区分矩阵，且P⊆C，如果P满足：1)∀φ≠m(i′,j′)∈M′，且P∩m(i′,j′)≠φ；2)∀a∈P,P′=P-{a}均不满足1)，则称P是C关于D的一个属性约简。

2.2　属性约简算法流程

通过基于粗糙集约简理论的改进区分矩阵设计，结合铁路专用线危险货物运输安全评价体系的特点，对该体系中指标精简的具体实施步骤如下：

Step1 确定属性集C，汇总现有成果，构建铁路专用线危险货物运输安全评价指标集C，其中ci∈C为铁路专用线危货运输安全评价指标；

Step2 确定样本集即论域U，其中ui∈U为历史数据中某个年度或某个时段的铁路专用线危险货物运输安全评价指标的取值；

Step3 属性值语义界定，确定每个评价指标ci的属性值以及相应评语集，并确定每个样本u关于属性a的信息值F(u,a)；

Step4 构建属性约简决策表S=(U,A,V,F)，结合各类指标评语集与历史数据构建类似于二维矩阵的关系数据表，该表中每一列数据代表论域中的一个样本，每一行代表论域中所有样本关于某个属性即评价指标ci的值；

Step5 确定评价体系指标属性集C的不可区分关系ind(C)，计算过程如下[15]：

1)对每一个指标ci(i=1,2,…,r)信息值函数值f(uj,ci)(j=1,2,…,n)的最大值和最小值，分别记为Mi与mi；

2)以静态链表依次存储对象u1,u2,…,un，令表头指针指向u1；

3)进行“分配”与“收集”

第i次“分配”：构建Mi-mi+1空对列，设置对列k的头指针和尾指针分别为frontk和frontk，并将链表中的对象u∈U按其在链表中的次序分配至队列f(u,ci)-mi中；

第i次“收集”：将表头指针指向第一个非空对列的头指针，并修改每一个非空对列的尾指针，令其指向下一个非空对列的对头对象，如此将Mi-mi+1个对列重组为一个链表；

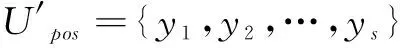
4)对于不为空集矩阵元素m(i,j)≠φ，如果该元素只有一个指标c，则将其并入集合reduce(C)，并将包含指标c所有矩阵元素去掉，然后在C-T-reduce(C)中取任意指标c*并入集合T，在所有包含指标c*的矩阵元素中去掉指标c*。

集合reduce(C)所包含的指标即为约简后的指标。

2.3　算法复杂程度分析

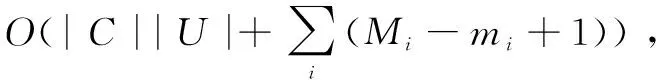
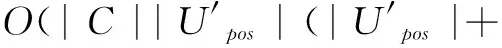
传统基于粗糙集属性约简算法时间复杂度为O(|C||U|2)，故基于改进区分矩阵的属性约简算法在时间复杂度上较原算法更优。

3　实例分析

以成都铁路局某家石化有限公司所属专用线为案例，结合路局安全监察网公布的2011—2016年专用线事故分析报告，组织10位铁路运输安全领域专家根据该公司实际状况，按照图1评价指标体系进行打分，选取10份构成信息决策表论域U={u1,u2,…,u10}，16个三级指标构成条件属性集C={c1,c2,…,c16}，二级指标安全程度等级构成决策属性D，如表1所示。

表1　专家打分样表Table 1　The expert scoring table

鉴于决策表属性值的离散数值表达特性，本文通过调研与专家问询确定各指标分级标准如表2所示，在此基础上进行数据离散化处理得到转化Rough Set数据，如表3所示。

表3中，决策属性d1,d2,d3,d4分别代表资质管理、安全设备设施、运输设备设施以及安全管理4个一级指标的评定结果，本文根据这4个一级指标的评定结果分别对其下属的二级指标进行约简。

根据Step6，构建简化的区分矩阵如表4所示。

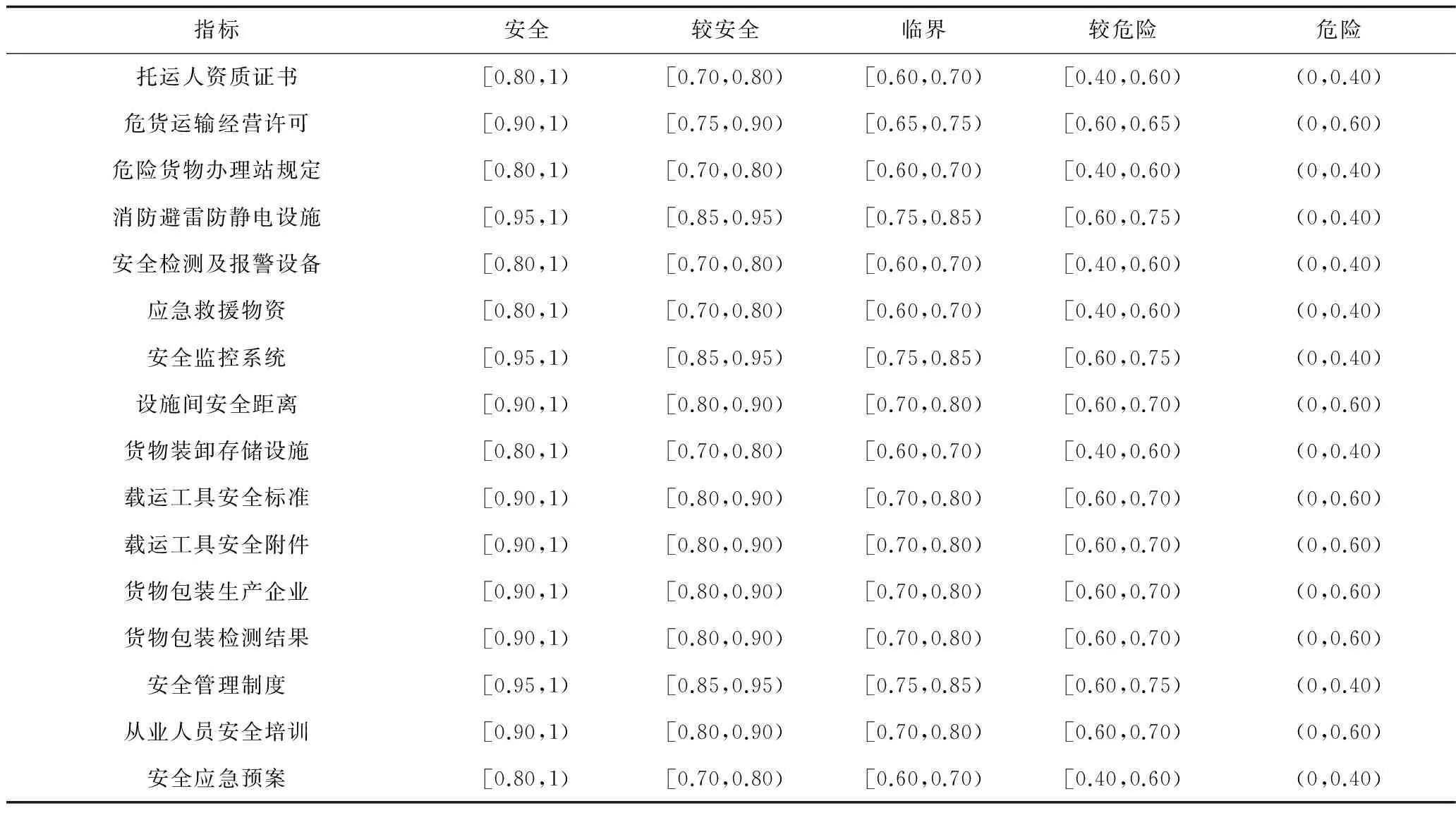
表2　指标分级标准Table 2　Index grading standard table

表3　原始数据转化Rough Set数据Table 3　Raw data converted into rough set data

表4　资质管理属性简化区分矩阵Table 4　Simplified discernibility matrix ofqualification management

根据表4，由Step6计算得到资质管理类指标的约简结果为reduce(C1)={c11,c12}，即托运人资质证书以及危货运输经营许可指标属于不可约简属性。

根据Step6，构建简化的区分矩阵如表5所示。

表5　安全设备设施属性简化区分矩阵Table 5　Simplified discernibility matrix of safetyequipment and facilities

根据表5，由Step6计算得到资质管理类指标的约简结果为reduce(C2)={c21,c24,c25}，即消防避雷防静电设施、安全监控系统以及设施间安全距离等指标均属于约简后需要保留的资质管理类指标。

同理，运输设备设施以及安全管理类指标的约简结果分别为reduce(C3)={c31,c32,c35}与reduce(C4)={c42,c43}，即货物装卸存储设施、载运工具安全标准以及货物包装检测结果属于约简后需要保留的运输设备设施类指标，从业人员安全培训以及安全应急预案属于约简后需要保留的安全管理类指标。

4　结论

1)基于改进区分矩阵的属性约简算法时间复杂度为O(|C||U|)，优于传统算法的时间复杂度O(|C||U|2)。

2)通过改进区分矩阵对决策表进行属性约简，得到了约简后的条件属性集为{c11，c12，c21，c24，c25，c31，c32，c35，c42，c43}，从而使决策表在具备原有的分类能力的基础上条件属性由原来的 16 个缩减为10个， 即：托运人资质证书、危货运输经营许可、消防避雷防静电设施、安全监控系统、设施间安全距离、货物装卸存储设施、载运工具安全标准、货物包装检测结果、从业人员安全培训以及安全应急预案，从而显著地简化了决策表。

3)约简后的剩余的属性是决定铁路专用线危险货物运输安全程度的关键要素，所以约简结果表明：在铁路专用线危险货物运输过程中，严格审查危货运输公司的资质与许可，加强工作人员的专业培训，以及严格审查各类运输设施设备的安全技术标准，可以切实保障专用线危险货物运输的安全生产与运营。

4)基于改进区分矩阵的指标属性约简，使得原铁路专用线危险货物运输安全评价体系的指标数减少了6个，评价体系更为简单清晰，从而减少了后续评价工作的计算量与复杂程度。

[1]王爽.铁路危险货物办理站及专用线运输安全现状综合分析与管理对策研究[D].北京：北京交通大学，2012.

[2]Glickman, Erkut. Assessment of hazardous material risks for rail yard safety [J]. Safety Science, 2007, 45:813-822.

[3]Cozzani, Bonvicini, Spadoni, et al. Hazmat transport: A methodological framework for the risk analysis of marshalling yards [J]. Journal of Hazardous Materials,2007,147(1/2) : 412-423.

[4]张江华，朱道立.危险化学品运输风险分析研究综述[J].中国安全科学学报，2007,17(3):136 -141.

ZHANG Jianghua, ZHU Daoli. Review on risk analysis of dangerous chemical transportation [J]. China Safety Science Journal, 2007,17(3):136 -141.

[5]王喆，彭其渊，蔡梦贤. 铁路危险货物办理站点优化配置方法研究[J].中国安全生产科学技术，2011,7(5):101-107.

WANG Zhe, PENG Qiyuan, CAI Mengxian. Research on optimization configuration method of railway dangerous goods stations and sidings [J]. Journal of Safety Science and Technology, 2011,7(5):101-107.

[6]王喆，蔡梦贤.基于突变理论的铁路危险货物办理站安全评价[J].武汉理工大学学报(交通科学与工程版)，2012,36(1):141-144.

WANG Zhe, CAI Mengxian. Catastrophe theory-based safety evaluation of railway dangerous goods station [J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2012,36(1):141-144.

[7]刘雪鹏，杨月芳，冯伟，等.铁路危险货物专用线运输安全分析方法研究[J].物流技术，2013, 32(11):155-159.

LIU Xuepeng, YANG Yuefang, FENG Wei. Study on analysis of transportation safety of dedicated dangerous cargo rail lines [J]. Logistics Technology, 2013, 32(11):155-159.

[8]Pawlak.Z. Rough sets: Theoretical Aspects of Reasoning about Data [M].Netherlands: Kluwer, Academic Publishers, 1992.

[9]徐章艳，杨炳儒，宋威.基于简化的二进制差别矩阵的快速求核算法[J].小型微型计算机系统，2006,(26):167-171.

XU Zhangyan, YANG Binru, SONG Wei. Quick computing core algorithm based on simply binary discernibility matrix[J].Journal of Chinese Computer Systems, 2006,(26):167-171.

[10]肖贵平,朱晓宁.交通安全工程[M].北京：中国铁道出版社，2004.

[11]陈亮.铁路危险货物运输安全综合分析研究[D].北京：清华大学，2013.

[12]王建春.铁路危险货物运输的安全隐患及对策[J].铁道货运,2004(9):22-24.

WANG Jianchun. Hidden danger and countermeasure of railway transportation of dangerous goods[J].Railway Freight Transport, 2004(9):22-24.

[13]沈小燕.道路危险货物运输企业安全评价研究[D].西安：长安大学，2006.

[14]邬云龙，刘丹龙，王浩然，等.基于粗糙集Skowron差别矩阵的矿井火灾风险评价指标约简[J].中国安全生产科学技术，2016,12(5):60-65.

WU Yunlong, LIU Danlong, WANG Haoran ，et al. Reduction of risk assessment indexes for mine fire based on Skowron discernibility matrix of rough set theory [J]. Journal of Safety Science and Technology, 2016,12(5):60-65.

[15]蒋瑜，王燮，叶振.基于差别矩阵的Rough集属性约简算法[J].系统仿真学报，2008,20(14): 3717-3720.

JIANG Yu, WANG Xie, YE Zhen. Attribute reduction algorithm of rough sets based on discernibility matrix [J]. Journal of System Simulation, 2008,20(14): 3717-3720.