基于Probit-Bayes方法的储罐地震易损性研究*
魏利军,王向阳,,罗艾民,向 阳
(1.中国安全生产科学研究院,北京 100012;2.北京化工大学 化学工程学院,北京 100029)
0 引言
储罐在地震的作用下会造成不同程度的损伤,严重的甚至会造成倒塌破坏。准确描述地震作用下储罐的损伤程度不仅可以对震后储罐的安全评估提供理论依据,还可以预测不同地震强度下的储罐损伤程度。国内外学者对储罐的地震易损性模型进行了一些研究。Krausmann等[1]整理了日本东北部海域发生的里氏9.0地震造成工业设施损害及危化品泄漏方面的资料,并分析了工业设备损害的主要原因及造成的严重后果,设备损害的主要原因为液面晃动、碰撞错位、刚性拉伸等因素,对于一些塔器、罐体等设备,其支撑支架翘曲断裂是引起事故的主要原因;E. Salzano等[2]通过整理500多起化工储罐发生损坏的事故,基于Probit模型,根据储罐不同的损伤状态,定量的描述了地震加速度和储罐损坏程度之间的关系。国内目前在定量评价地震对储罐的灾害程度方面的研究较少,杨维国等[3]分析国内外各类工业设备的震害数据,以设备遭受地震的损坏程度为依据,综合考虑可使用程度,修复的难易程度和所需经费,将其震害划分为基本完好、轻微损坏、中等损坏、严重损坏和毁坏5个等级;张令心等[4]结合以往的震害经验和地震对企业的影响程度等方面,对化工设备的破坏等级进行了划分,但没有定量的描述2者的关系;孙建刚等[5]提出了基于概率估计方法研究储罐失效模式的地震易损性,绘制出了易损性曲线图。
Bayes方法是一种基于概率的不确定性推理模型,通过学习和推理,可以利用一些先验知识对某些现象进行识别、分类和推理[6-7]。在研究多米诺效应扩展概率方面,Probit分析方法[8]作为计算多米诺事故的传播概率得到广泛的应用,在分析多米诺事故扩展方式的基础上,利用Probit模型推导出了超压模型[9]、热辐射模型[10]及毒物中毒模型[11]等模型。由于该模型的简单性及在有足够数据的基础上,可将其利用于其他因素造成工艺设备损伤的概率计算,因此,这一工具也逐渐适用于危险性评估方面,如储罐的地震危险性评估。Fabbrocino等[12]利用Probit模型对常见的几种设备进行了评估分析,并利用QRA计算方法初步评估了车间内的风险值;Ernesto Salzano等[13]基于历史数据和Na-Tech的研究方法分析了工业设备(如储罐、反应器等)受地震的影响,选取峰值地面加速度(PGA)和设备特定脆性曲线来分析受灾情况,计算损伤概率值,并利用PGA表示设备的损伤阈值,为预警系统、地震减缓提供了指导性意见。因此,本文基于Probit模型的先验知识,并通过Bayes进行推理,得出地震对储罐的影响,并绘制了储罐的易损性曲线。
1 地震易损性评估步骤
本文提出的地震易损性评估方法,是通过Bayes方法对Probit模型中的参数进行估计,再构建理论易损性曲线,对储罐进行损伤估计,其基本步骤如下:
1)收集历史数据,通过定义储罐不同的损坏形式,将所得到的数据整理,进行损伤等级划分。
2)通过对数据进行回归分析,建立储罐的失效概率函数,其中以地震的地面加速度为自变量,在参数估计时采用贝叶斯估计。
3)计算不同强度地震动参数下储罐超过某一损坏状态下的失效概率。
4)绘制以地面加速度为自变量的地震易损性曲线。
2 地震损伤评估方法
2.1 Probit模型
关于储罐损伤概率的研究主要以Probit模型来定量计算由于地震造成的储罐损伤:
Y=k1+k2ln(PGA)
(1)
式中:Y为设备损伤概率对应的正态偏差或Probit值;PGA为地震加速度;k1,k2为模型系数。
然后再由公式(2)可以得出设备的损伤概率F值:
(2)
由此方法,则可以将一定的地震强度造成的储罐损坏程度进行量化,得出储罐损坏概率。
2.2 Bayes参数估计
估计系数k1和k2时,首先假设误差分布形式为正态分布,即采用由下列结构构成的模型估计参数。该模型的表达式为:
Y=k1+k2ln(PGA)+ε
(3)
式中:ε为误差项。为简化计算,假设ε~N(0,σ2I),则其贝叶斯模型可简化为:Y=k1+k2ln(PGA)+ε,ε~N(0,σ2I);P(k1)∝1;P(k2)=(k2|μ,τ)~N(μ2,τ2);μ2∝1;k1,k2为待估参数,假设具有上述的先验分布;μ2为未知超参数,假设无先验信息;σ,τ2为讨厌参数,2者为缺损参数。
基于以上的条件,可以写出模型对应的似然函数为:

(4)
式中:D为样本数据;θ为未知参数,即θ=(k1,k2)。
根据Bayes原理,在给定观测数据D时参数的后验概率分布表示为:
P(k1,k2,μ2|Y1,Y2,…,Yn,σ,τ2)=
(5)
式中:θ,μ2均为待估参数,θ=(k1,k2)。利用上式,分别计算出参数k1,k2的后验概率为:
(6)

再根据Bayes理论,采用Gibbs随机采样求得参数后验概率分布的数值解,其步骤如下:
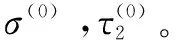
(7)
6)根据抽样的方法得到一定数量的参数估计值,进而计算待估参数的期望估计。
2.3 地震易损性曲线
地震易损性是指在某一特定强度地震作用下,储罐达到或者超过某一级别破坏状态时的失效概率,其表达式为:
FR(a)=P(LS|A=a)
(8)
式中:a为地震动参数,如地震峰值加速度。通过改变该值,计算储罐达到或者超过损伤状态LS的易损性FR,然后采用某种方法进行线性拟合,得到的曲线即为储罐的地震易损性曲线[14]。
通过上节得到的参数估计值后,计算不同地震加速度下的Probit值,再通过式(2),计算得出相应的损伤概率值,然后绘制成易损性曲线。
3 模型应用
本文搜集了历史上国内外部分地震[15]的震害资料,并进行了一定的整理、分析,如表1所示:

表1 储罐的地震灾害基础数据集Table 1 Database of the storage tanks
通过参考地震对设备的破坏程度的震灾评估标准[16],将储罐的震害程度分为5类:DS=1,基本完好,无明显震害;DS=2,轻微损坏,进出口管线断裂;DS=3,中度损坏,罐体下沉或倾斜,轻度泄漏;DS=4,大规模损坏,罐体严重下沉或倾斜,象足式破坏;DS=5,完全损坏,罐体倒塌,被砸扁。根据上述标准,对收集的地震灾害造成的储罐事故后果进行分析整理得表2:

表2 储罐损坏程度数据表Table 2 Database of storage damage state
再利用第2节中描述的Bayes模型估计Probit模型参数,得到下表3:

表3 Probit模型参数Table 3 The parameters of Probit model
利用上述参数估计值,计算不同地震加速度下的Probit值,再通过式(2)计算得出相应的损伤概率值,然后绘制成易损性曲线。

图1 储罐的易损性曲线Fig.1 The seismic vulnerability curves of tanks
在获得地震易损性曲线后,可以确定储罐在给定地震作用下的损伤概率值。如图所示,随着PGA的增加,各损伤状态下的易损性曲线都随之增大。DS≥2和DS≥3对应的易损性曲线在地震加速度PGA小于0.4g时,损伤概率值增大较快,之后曲线增长速度变缓,2者达到的最大值分别为70%和47%,虽然地震的破坏程度较大,但是不可能对所有储罐造成严重的损伤,因此2者的概率值不可能达到100%,从表1中的数据也可以证明这一点,所以该曲线更切合实际情况。同样的,当DS≥4和DS=5时也可以得到类似的结论。因此,通过该方法可求得给定地震作用下的储罐损伤概率值。
4 结论
1)针对储罐的地震易损性研究问题,提出了1种基于Probit模型,结合Bayes参数估计方法的地震易损性评估方法。
2)通过概率估计的形式,量化了地震加速度与储罐损伤程度之间的关系,且模型中各个参数容易确定,能够快速得出储罐在地震作用下的损伤概率值,为震后储罐的安全评估提供了理论依据。
3)该估计方法需要实际的灾害评估结果作为数据,但是现有的基于地震的事故数据还不是很完整,收集的样本数据评定标准可能有所不同,造成估计后的概率值存在差异。目前该方面的研究还没有成熟的理论,孰优孰劣还不能完全的确定,但本文所采用的算法为量化地震强度与储罐损伤程度提供了1种方法。
[1]Krausmann E, Cruz A M. Impact of the 11 March 2011, Great East Japan earthquake and tsunami on the chemical industry[J]. Natural Hazards, 2013, 67(2):811-828.
[2]Salzano E, Iervolino I, Fabbrocino G. Seismic risk of atmospheric storage tanks in the framework of quantitative risk analysis[J]. Journal of Loss Prevention in the Process Industries, 2003, 16(5):403-409.
[3]汤天伟,许成祥,马成松.石化企业震害评估指标及生产设备震害分析[J].江汉石油学院学报,2000,22(1):22-23.
TANG Tianwei, XU Chengxiang, MA Chengsong. Seismic damage assessment of petrochemical enterprises and damage analysis of equipment[J]. Journal of Jianghan Petroleum Institute. 2000,22(1):22-23 .
[4]张令心, 郭宁, 刘洁平. 工业设备地震破坏等级划分[J]. 自然灾害学报, 2013, 22(6):57-63.
ZHANG Lingxin, GUO Ning, LIU Jieping. Classification of earthquake damage to industrial equipment[J]. Journal of Natural Disasters. 2013,22(6):57-63.
[5]孙建刚,张荣花,张亮.基于概率估计方法的立式储罐地震易损性研究[J].世界地震工程, 2009,25(1):37-42.
SUN Jiangang, ZHANG Ronghua, ZHANG Liang. Investigation on seismic vulnerability of vertical storage tanks based on probability estimate method[J]. World Earthquake Engineering. 2009,25(1):37-42.
[6]付钰,吴晓平,严承华.基于贝叶斯网络的信息安全风险评估方法[J].武汉大学学报:理学版,2006,52(5):631-634.
FU Yu, WU Xiaoping, YAN Chenghua. Information security risk assessment method based on bayesian network[J]. Journal of Wuhan University (Nat. Sci. Ed.). 2006,52(5):631-634.
[7]顾一波,霍宇芒. 基于贝叶斯网络的地震次生燃气管道泄漏事件链构建[J].中国安全生产科学技术,2016,12(7):134-139.
GU Yibo, HUO Yumang. Construction of eevent chain for secondary gas pipeline leakage induced by earthquake based on bayesian network[J]. Journal of Safety Science and Technology. 2016,12(7):134-139.
[8]Ví Lchez J A, Montiel H, Casal J, et al. Analytical expressions for the calculation of damage percentage using the probit methodology[J]. Journal of Loss Prevention in the Process Industries, 2001, 14(3):193-197.
[9]Cozzani V, Salzano E. The quantitative assessment of domino effects caused by overpressure. Part I. Probit models[J]. Journal of Hazardous Materials, 2004, 107(3):67-80.
[10]Uijt de Haag PAM, Ale BJM. Guidelines for quantitative risk assessment (purple book) [M]. The Hague, Committee for the Prevention of Disasters. 1999:123-126.
[11]Center for Chemical Process Safety. Guidelines for consequence analysis of chemical releases[M]. New York:American Institute of Chemical Engineers, 1999:254-255.
[12]Fabbrocino G, Iervolino I, Orlando F, et al. Quantitative risk analysis of oil storage facilities in seismic areas.[J]. Journal of Hazardous Materials, 2005, 123(1-3):61-69.
[13]Salzano E, Agreda A G, Carluccio A D, et al. Risk assessment and early warning systems for industrial facilities in seismic zones[J]. Reliability Engineering & System Safety, 2009, 94(10):1577-1584.
[14]吕大刚, 李晓鹏, 王光远. 基于可靠度和性能的结构整体地震易损性分析[J]. 自然灾害学报, 2006, 15(2):107-114.
LYU Dagang, LI Xiaopeng, WANG Guangyuan. Global seismic fragility analysis of structures based on reliability and performance[J]. Journal of Natural Disasters. 2006,15(2):107 -114.
[15]American Lifelines Alliance. American lifeline alliance seismic fragility formulation for water system: part 2-appendices[M]. New York:The American Society of Civil Engineers,2001:80-147.
[16]中华人民共和国住房和城乡建设部.石油化工工程地震破坏鉴定标准: GB/T 50992-2014[S].北京:中国计划出版社,2015.
—— 储罐

