基于贝叶斯网络的化工园区地震次生灾害情景分析*

魏利军，王向阳,，罗艾民，多英全，王如君，向　阳

(1.中国安全生产科学研究院，北京 100012； 2.北京化工大学 化学工程学院，北京 100029)

0　引言

地震作为一种突发性强、不确定性高的自然灾害，不仅仅会直接造成极大的破坏及人员伤亡，同时由于化工园区内危险化学品的存在，极易造成泄漏、火灾或爆炸等严重的化工事故，给地震应急救援工作带来了极大的困难[1]。为了探明地震灾害化工事故演化机理，国内外学者做了大量的研究。余世舟等[2]在地理信息系统(Geographic Information System，GIS)支持下利用火灾、爆炸及毒气泄漏和扩散的数学模型，对地震次生灾害进行了数值模拟，可以直观的给出地震次生灾害的危害范围；之后，余世舟等[3]利用灾害链理论分析破坏性地震引发化工次生灾害的成灾机理，并构建定量的概率分析模型，找出灾害链中的关键节点，采取断链措施，减少人员伤亡及财产损失；Salzano等[4]利用历史上地震灾害的事故调查结果，采用Probit模型，定义储罐不同损伤状态，定量的描述了地震加速度(PGA)和储罐损坏程度之间的关系；Fabbrocino等[5]和Antonioni等[6]在此基础上，利用定量风险评价(QRA)的方法，评估地震造成的化工事故后果，得到个人风险和社会风险，从而为震前预测提供指导性意见；Krausmann E等[7]基于Natech事件评估方法对地震、洪水等自然灾害造成的化工设备失效事故进行了研究分析，其主要是研究自然灾害对化工装置造成的初步事故，而未考虑由其引发的多米诺事件。上述文中均未深层次描述事故的演化过程，而在量化研究耦合演化过程的问题上，贝叶斯[8-10]具有明显的优势，可依靠条件概率表达各风险节点之间的相互作用关系。因此，本文通过构建贝叶斯网络结构图，研究地震灾害化工事故演化过程，为探索地震灾害对园区影响提供新的思路。

本文通过灾害链理论对地震灾害化工事故灾害机理进行分析，并将其转化为贝叶斯网络，构建化工园区地震灾害的演化机理模型，再确定各节点变量及各自的取值范围，通过相关文献及专家经验判断分析，获得贝叶斯网络中各节点的条件概率值；最后，本文将对比不同地震烈度下，各化工事故发生的后验概率，并探讨应急救援及遏制化工事故发生的关键节点对地震次生灾害的影响程度。

1　地震灾害事故链反应机理分析

由一种灾害引发另一种灾害或其他一系列灾害的现象称为灾害链，自然灾害属于典型的灾害链[11-12]。根据该理论，由地震引发的化工事故是一种典型的链式结构，是一种以地震灾害为外因，从而诱发化工装置破坏及失效等内因的链式过程。根据地震灾害事故的特点，将地震灾害的诱发外因及其致灾的过程称为灾害链的启动环，把因地震灾害造成化工装置损坏或者泄漏等事故类型称为激发环，泄漏事故及点火源相互作用造成火灾、爆炸等化工事故称为演化环，该灾害造成的事故后果及损失称为损害环。地震灾害诱发化工事故的形成与演化过程作为一种典型的灾害链类型，其危险性、灾害性都十分巨大，且一灾多链、连锁反应，造成的事故后果严重。地震灾害诱发化工事故的灾害链反应特征总结如图1。

图1　地震诱发化工事故的灾害链Fig.1　Earthquake-induced chemical accident disaster chain

2　事故链转化为贝叶斯网络

贝叶斯网络用有向无环图的形式表达随机变量间的关联特性，用条件概率分布的形式表示关联强度[13]。因此，基于贝叶斯模型在处理不确定性方面的优势，可将上述的事故链模型转化为贝叶斯网络对地震灾害化工事故演化过程进行定量分析。

2.1　网络节点变量及结构

地震次生化工事故演化过程可分为园区内储罐、管道、化工设备及建筑物受地震作用破坏，火灾、中毒及爆炸等化工事故，地震发生后的应急救援，人员伤亡及经济损失等4个层次，将其分别对应上述事故链的各个环节，构建地震化工事故演化过程的贝叶斯网络结构图，贝叶斯网络由节点和有向的弧线组成，是一个有向无环图，如图2所示。

本文主要探讨地震强度对化工园区的影响，着重分析地震烈度的影响程度，因此将地震烈度作为主要的证据变量。当地震发生后，储罐、管道、化工设备及建筑物会遭受不同程度的破坏，上述各个装备均要考虑。设备破坏后，可能会造成有毒或易燃易爆原料及产品的泄漏，从而引发中毒、火灾及爆炸等化工事故。除了泄漏后遇点火源发生火灾爆炸外，生产设备由于辅助设施失效等原因，造成内部压力过大，也会发生物理爆炸。事故发生后，若交通阻断或者应急物资等因素，造成应急救援不及时，会造成更为人员伤亡及经济损失，该模型中，主要考虑化工事故造成人员伤亡的后果类型。

2.2　网络节点变量取值及条件概率设置

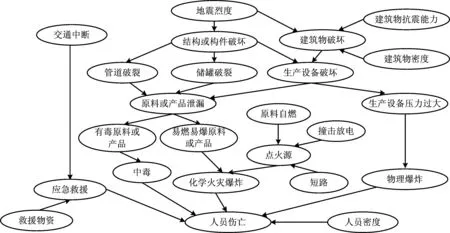
图2　化工园区地震灾害演化机理Fig.2　Evolution mechanism of earthquake disaster in chemical industry park

若假设网络中各个父节点变量为连续性概率分布，则其对应的子节点变量也为连续分布，这会造成后验概率参数估计的复杂性，且目前已有研究中所给出的参数估计的经验公式，均对各个节点变量进行离散化处理， 因此本文也将各个节点进行离散化处理。由于本文主要探讨地震强度对化工园区的影响程度，主要将地震烈度分为7，8，9，10共4组，其他网络节点变量均为{是，否}2个状态值。部分节点变量状态分布见表1。

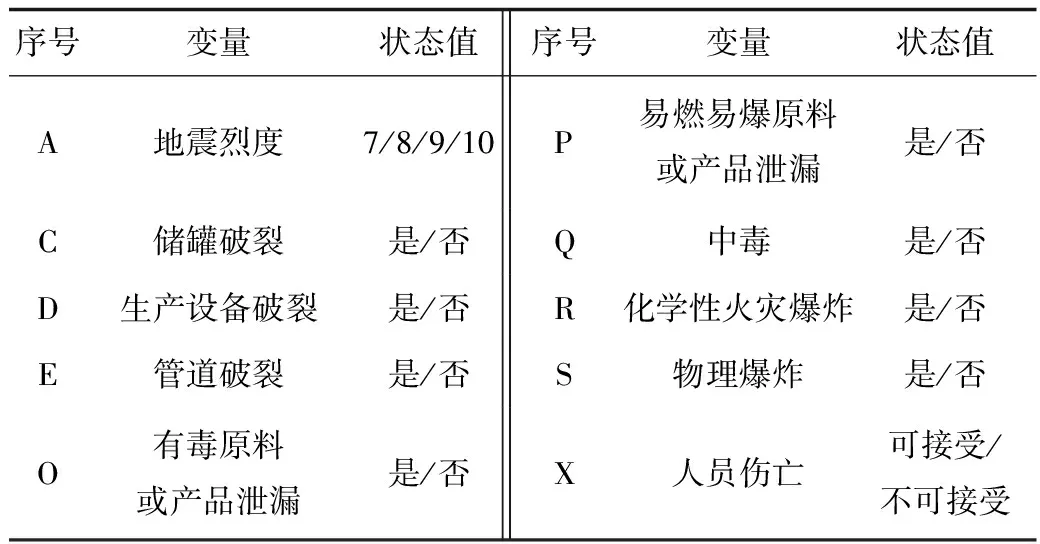
表1　贝叶斯网络中部分节点状态变量离散化分布

在上述节点变量离散化的基础上，需确定每一个节点的条件概率值。节点条件概率分布表给出了各个节点的先验概率值，即人们事先对该事件发生可能性大小的参数估计。由于目前国内外相关统计数据不能给出所建立贝叶斯网络模型所需要的数据，因此本文参考了相关文献[3,9,14]数据，并结合专家意见，给出各个节点的条件概率经验判断值。以化学性火灾爆炸为例，其条件概率表如表2所示。

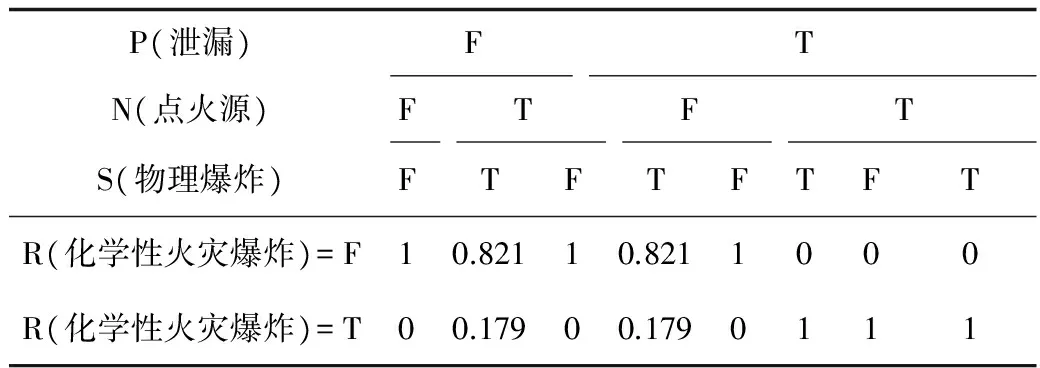
表2　“化学火灾爆炸”节点的条件概率表

从上表可看出：当存在易燃易爆原料或产品的条件下，遇点火源后会发生化学性火灾爆炸事故；或者由于物理爆炸引发化学性火灾爆炸事故，其概率为0.821。

3　模型应用

采用上述构建的贝叶斯网络模型对某种特定场景下地震灾害的演化过程进行推理计算分析。若某化工园区内的厂房或者中控室等建筑物抗震能力强，且建筑物分布比较稀少，可认为建筑物密度低；化工园区内都设有消防队及消防物资，以保障园区发生化工事故后，可尽快到达事故现场；地震发生在白天，园区内的工作人员都在正常上班，可认为人员密度较高。根据以上的条件，对贝叶斯网络中相关节点变量的先验概率进行设定，其他未涉及的节点均采用上一节中所给出的先验概率值，并通过贝叶斯网络计算得到网络中各个节点的后验概率值。输入Netica软件得到化工园区地震灾害化工事故演化过程的贝叶斯模型图，如图3所示。

破坏性地震可能会造成园区内储罐、生产设备及管道发生破裂，致使内部危险化学品发生泄漏，造成中毒、物理爆炸、化学性火灾爆炸等化工事故，使得人员伤亡。由图3可知：假设该地区发生9级烈度地震时，园区内储罐的破裂概率为0.405，同时由于地震灾害及建筑物倒塌造成生产设备破裂的概率为0.147，管道的破裂概率为0.32，从这三者的概率值可以看出，储罐的破裂概率要高于其余两项，主要原因为园区内的主要原料或产品存放在储罐中，造成其数量较多，且储罐内化学品受到其地震作用，发生晃动等，致使储罐破裂的概率高于其余设备。当设备发生破裂后，会造成不同程度的泄漏，本文仅对泄漏的化学品作了简单的划分，未对泄漏的程度进行分级；由于受到原料或产品泄漏节点的约束，且园区内有毒可扩散物质种类相比于易燃易爆化学品较少，导致有毒原料或产品节点概率为0.052 6，易燃易爆化学品节点概率为0.206，之后，造成的中毒、化学性火灾爆炸及物理爆炸节点概率分别为0.042，0.115及0.026 4，当得到上述概率后，由于园区内应急救援和人员密度等节点的影响，造成人员伤亡不可接受的概率变为0.021。

图3　化工园区地震灾害贝叶斯网络结构Fig.3　Bayesian network structure of earthquake disaster in chemical industry park

变量名称取值7级后验概率值8级后验概率值9级后验概率值10级后验概率值地震烈度7/8/9/10(1，0，0，0)(0，1，0，0)(0，0，1，0)(0，0，0，1)储罐破裂是/否(0．063，0．937)(0．18，0．82)(0．405，0．595)(0．648，0．352)生产设备破裂是/否(0．0225，0．9775)(0．644，0．9356)(0．147，0．853)(0．227，0．773)管道破裂是/否(0．0498，0．9502)(0．142，0．858)(0．32，0．68)(0．513，0．487)有毒原料或产品泄漏是/否(0．0081，0．9919)(0．023，0．977)(0．0526，0．9474)(0．084，0．916)易燃易爆原料或产品泄漏是/否(0．0316，0．9684)(0．0903，0．9097)(0．206，0．794)(0．33，0．67)中毒是/否(0．0064，0．9936)(0．0184，0．9816)(0．042，0．958)(0．0672，0．9328)化学性火灾爆炸是/否(0．0177，0．9823)(0．506，0．9494)(0．115，0．885)(0．183，0．817)物理爆炸是/否(0．004，0．996)(0．0115，0．9885)(0．0264，0．976)(0．0407，0．9593)人员伤亡不可接受/可接受(0．0035，0．9965)(0．0098，0．9902)(0．021，0．979)(0．0383，0．9617)

根据表3的计算结果：随着地震烈度的增大，其化工设备的破裂概率值明显升高，以储罐为例，7，8，9，10级烈度值下其后验概率值分别为0.063，0.18，0.405，0.648，将其值与文献[5]中的概率值(0.07，0.2，0.45，0.72)对比，可知其后验概率值符合其变化趋势，但是当烈度值较大时，其概率值小于文献中的概率值，原因可能为以贝叶斯方法模拟时，该方法对先验概率值有一定的修正，不仅仅考虑了历史数据，还加入了相关专家意见的先验概率值，从而造成该值小于文献中的值。

随着地震烈度的增大，其事故后果概率值也有一定程度的增大，但是其中毒、化学性火灾爆炸及物理爆炸概率的增长幅度相比于化工设备增长幅度相比有所降低，分别为0.006 4～0.067 2，0.017 7～0.183，0.004～0.040 7。可见，地震烈度对化工设备直接破坏的概率影响较大，但是由于存在中间多个节点变量的约束，其对事故后果的影响相对较弱。

随着地震烈度的增大，其人员伤亡概率也有所提高，统计2008—2014年全国化工和危险化学品典型事故案例时，在非自然灾害化工事故中，人员伤亡不可接受的概率为0.003，可见当发生9～10级烈度地震时，人员伤亡概率值会增大一个数量级，该结论与文献[15]中的结论一致，文献中描述的是大型地震会造成PLL值会增大1～2个数量级。

同理，以9级烈度的地震为例，当地震发生时，若化工事故及人员伤亡成为事实，在建筑物属性等因素不可控的情况下，若采用适当科学的救灾措施，使应急救援能够及时，化工园区内部的人员密度降低，可使人员伤亡概率的损失达到最小，按照上述的思路，将贝叶斯网络中应急救援及人员密度改变不同的参数值。

表4　应急救援对人员伤亡的后验概率值影响程度

由表4计算结果可知：当应急救援及人员密度处于同一状态时，从危险性的角度考虑，应急救援的危险性较大，这是由于化工事故可能不会造成人员当场死亡，更多的是救援不及时，致使人员抢救无效死亡，因此应着重加强救援工作，如当地震发生后，应及时回复交通、电力系统，使节点回复正常，而当人员密度均为大时，由于救援不及时，会造成人员的伤亡不可接受概率值从0.019 8增加为0.024 5。

4　结论

1)将地震灾害化工事故演化过程分为园区内储罐、管道、化工设备及建筑物受地震作用破坏，火灾、中毒及爆炸等化工事故，地震发生后的应急救援，人员伤亡及经济损失4个层次，每个层次分别对应事故链的各个环节，完成由事故链转化为贝叶斯网络图的过程。

2)根据各节点的先验概率值，选定特定场景进行贝叶斯推理分析，对比不同地震烈度下的化工事故后果及人员伤亡情况，并探讨应急救援的及时及有效性对地震次生灾害发生概率的影响程度。

3)概率评估方法需要实际的次生灾害评估结果作为计算参数，但是现有的评估方法不统一，而且基于地震的事故信息不完整，其现有的概率数据只能基于少量的数据及专家意见来确定，造成其适用范围，应用条件有限，该方面应进一步研究。

[1]赵振东,王桂萱,赵杰.地震次生灾害及其研究现状[J].防灾减灾学报,2010,26(2):9-14.

ZHAO Zhendong, WANG Guixuan, ZHAO Jie. Secondary disaster of earthquake and the present research situation[J]. Journal of Disaster Prevention and Reduction, 2010, 26(2):9-14.

[2]余世舟,赵振东,钟江荣.基于GIS的地震次生灾害数值模拟[J].自然灾害学报,2003,12(4):100-105.

YU Shizhou, ZHAO Zhendong, ZHONG Jiangrong. Numerical simulation of secondary disasters of earthquake based on GIS[J].Journal of Natural Disasters, 2003,12(4):100-105.

[3]余世舟,张令心,赵振东,等.地震灾害链概率分析及断链减灾方法[J].土木工程学报,2010, 43(S1)：479-483.

YU Shizou , ZHANG Lingxin , ZHAO Zhendong, et al. Probability analysis of earthquake disaster chain and chain-cutting disaster mitigation method[J].China Civil Engineering Journal, 2010, 43(S1)：479-483.

[4]E. Salzano, I. Iervolino, G. Fabbrocino. Seismic risk of atmospheric storage tanks in the framework of quantitative risk analysis[J]. Journal of Loss Prevention in the Process Industries,2003(16):403-409.

[5]Giovanni Fabbrocino, IunioIervolino, Francesca Orlando, et al. Quantitative risk analysis of oil storage facilities in seismic areas[J]. Journal of Hazardous Materials, 2005,123(1):61-69.

[6]Giacomo Antonioni, GigliolaSpadoni, Valerio Cozzani. A methodology for the quantitative risk assessment of major accidents triggered by seismic events[J]. Journal of Hazardous Materials,2007,147:48-59.

[7]Elisabeth Krausmann, Ana Maria Cruz. Impact of the 11 March 2011, Great East Japan earthquake and tsunami on the chemical industry[J]. Natural Hazards,2013,67(2):811-828

[8]姚锡文,许开立,王贝贝,等.石化装置火灾爆炸贝叶斯网络与防护层集成分析[J].中国安全生产科学技术,2014,10(3):95-100.

YAO Xiwen, XU Kaili, WANG Beibei,et al.Integrative analysis of Bayesian networks and LOPA for fireand explosion in petrochemical plant[J].Journal of Safety Science and Technology,2014,10(3):95-100.

[9]马祖军,谢自莉.基于贝叶斯网络的城市地震次生灾害演化机理分析[J].灾害学,2012，27(4):1-5.

MA Zujun, XIE Zili. Evolution mechanism of earthquake-induced urban disasters based on Bayesian network[J]. Journal of Catastrophlogy, 2012,27(4):1-5.

[10]朱婷,赵来军,王旭磊.基于贝叶斯网络的危险化学品道路运输事故分析[J].安全与环境学报,2016,16(2):53-60.

ZHU Ting, ZHAO Laijun,WANG Xulei. Analysis of the hazardous material transportation accidensbased on the Bayesian network method. Journal of Safety and Environment,2016,16(2):53-60.

[11]史培军.三论灾害研究的理论与实践[J].自然灾害学报,2002,11(3):1-9.

SHI Peijun. Theory on disaster science and disaster dynamics[J]. Journal of Natural Disasters, 2002,11(3):1-9.

[12]尹卫霞,王静爱,余翰,等.基于灾害系统理论的地震灾害链研究—中国汶川“5.12”地震和日本福岛“3.11”地震灾害链对比[J].防灾科技学院学报,2012,14(2):1-8.

YIN Weixia, WANG Jingai, YU Han, et al. Study of earthquake disaster chains based on disaster system theory—comparison of disaster chains between the 12 May Wenchuan earthquake in China and the 11 March Tohoku earthquake in Japan[J]. Journal of Institute of Disaster Prevention, 2012,14(2):1-8.

[13]Javier Alvarez Galvez. Discovering complex interrelationships between socioeconomic status and health in Europe: A case study applying Bayesian Networks[J]. Social Science Research,2016,56(1):133-143.

[14]Michela Campedel，Valerio Cozzani, Anita Garcia-Agreda, et al. Extending the quantitative Assessment of Industrial Risks to Earthquake Effects[J]. Risk Analysis,2008,28(5):1231-1246.

[15]颜峻,左哲.建筑物地震次生火灾的贝叶斯网络推理模型研究[J].自然灾害学报,2014,23(3):205-212.

YAN Jun, ZUO Zhe. Study on inference model of seismic secondary fire of building based on Bayesian networks[J].Journal of Natural Disasters, 2014,23(3):205-212.