探索椭圆周长和椭球表面积的近似初等公式

四川省西昌市第一中学(615000)

周园钞●

探索椭圆周长和椭球表面积的近似初等公式

四川省西昌市第一中学(615000)

周园钞●

以信息技术、多媒体为手段，用初等数学方法探索椭圆周长和椭球表面积的近似初等公式.

函数;极限;椭圆周长;椭球表面积.

椭圆周长和椭球表面积的计算，由于其积分式的原函数不是初等函数，因而在中学数学中成了一块盲区.

本文以信息技术、多媒体为手段，应用初等数学的研究方法，推导、检验和应用椭圆周长和椭球表面积的近似初等公式.

一、椭圆周长近似初等公式的推导

根据微积分基本定理，通过定积分运算得到椭圆面积公式：S椭圆=π·ab……(1)

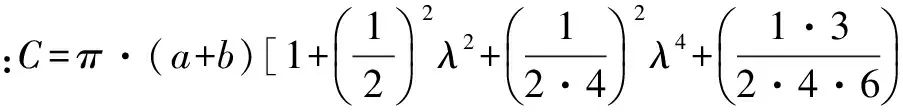
在(2)式中，我们设：

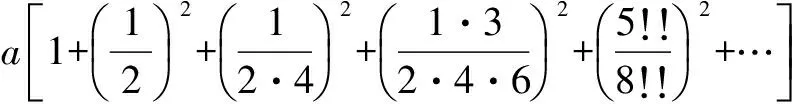
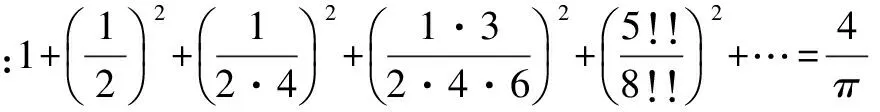
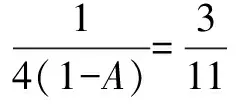
三、椭球表面积初等公式的类推

椭球的体积可以由定积分求出，其公式为：

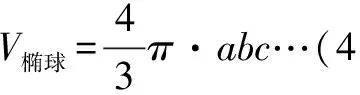
式中a,b,c分别为椭球的三个半轴长.

于是，用待定系数法，可设椭球表面积为(x，y为待定系数)：

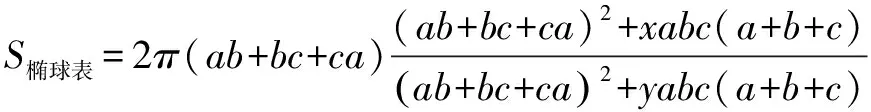
又，当a,b,c三者趋近相等时，椭球表面积为一个球的表面积，即4πa2.

令a=b=c=1

得：S=4π，

故4π=6π(9+3x)/(9+3y).

解得：y=(3x+3)/2.

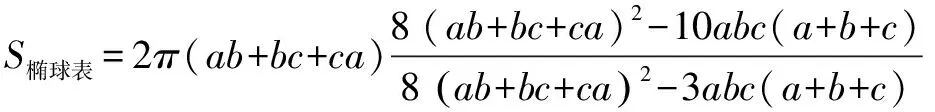
这个对称、美丽的椭球表面积初等公式，与椭圆周长一样简便好记：a,b,c齐次对称，且当a,b,c之一，例如c→0时，椭球表面积S→2πab；当c→b→a时，S→4πa2.为验证其精度，现用旋转椭球体的表面积的精确值加以对比：

表1 旋转椭球表面积分布表

表1虽然是用旋转椭球的表面积验证公式(5)，但由于公式(5)关于三半轴长完全对称，由排序不等式和椭球表面积的有关知识可知，任意三轴椭球表面积的误差低于表中相应位置的误差.

G632

B

1008-0333(2017)07-0014-02