化静为动求线段长度最值的尝试

武汉市黄陂区前川街道鲁台中学(432200)

沈永宽●

化静为动求线段长度最值的尝试

武汉市黄陂区前川街道鲁台中学(432200)

沈永宽●

求动态问题中线段长度的最值是近年来数学中考的热点内容，对学生来说解题的难度较大.尽管老师用了不少的方法引导学生解题，但能“消化”的学生不多.本文谈谈构建模型来攻克这一难关.

线段长度；最值；动态

一、构建三角形，运用三边关系定理模型

某些动态线段长度的最值，学生很难从静止的图形中求出来，甚至有时觉得束手无策.教师可运用课件，适当添加辅助线，让图形“动”起来，在图形运动的过程中引导学生构建三角形三边关系，从而求出最值.

二、构建圆，运用点与圆的距离极值模型

一个三角形的一边和它所对的角为定值，则这个角的顶点的轨迹是以这边为弦这个角为圆周角的两条弧(特别当这个角是直角时，这个角的顶点在这边为直径的两个半圆上).

由题目中的已知点或三角形作圆，再在圆中移动线段或点，根据圆形中直径的长度大于弦的长度以及点到圆的最大距离和最小距离为经过这点和圆心的直线与圆的两个交点间的距离，便可求得动态线段的最值.

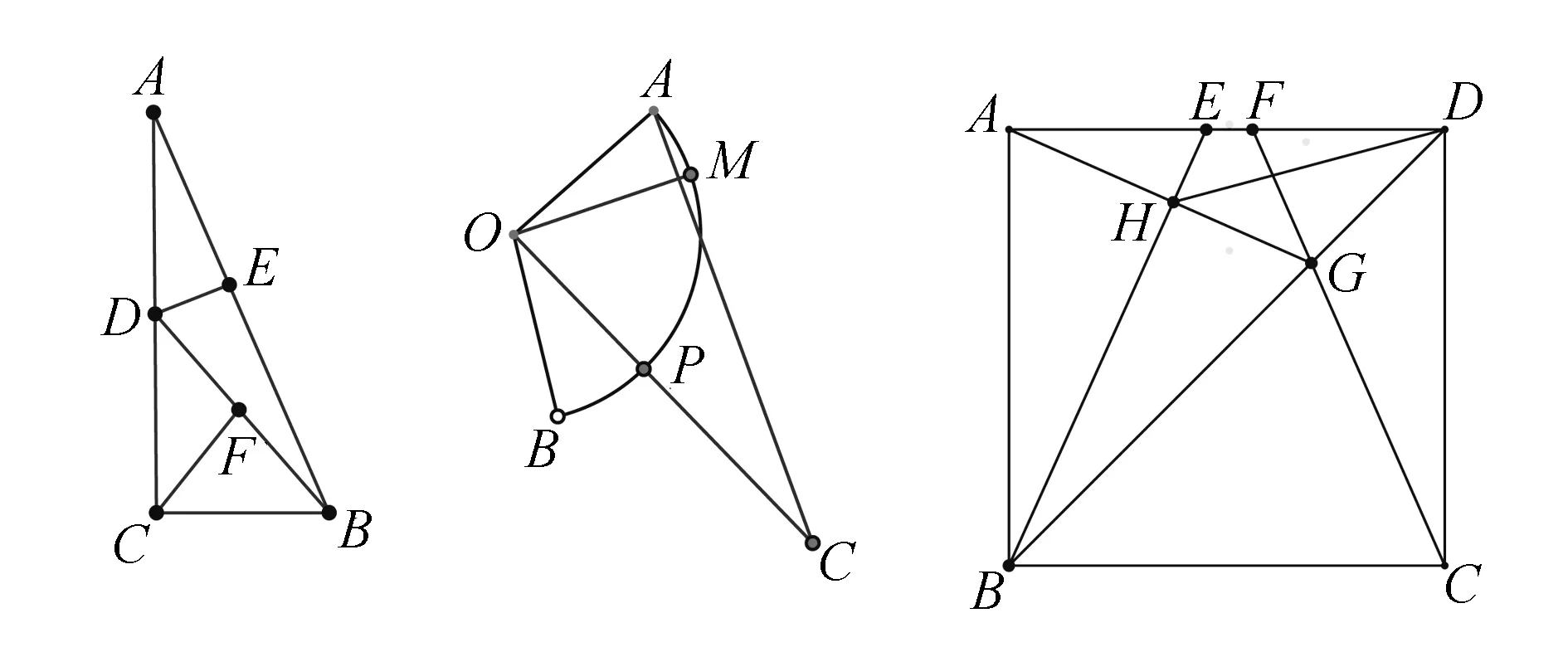
1.如图，扇形OAB的半径OA=2，M为弧AB上一点，∠AOM=30°，P为弧BM上一点，C为OP的延长线上一点，且∠ACO=30°，当P点运动时，则线段AC的最大值为____，最小值为____.先作△AOC的外接圆，再在圆上移动C点，通过观察，发现当AC为圆的直径时，AC的长度最大，最大值为4；当C点运动到OM的延长线上时，AC的长度最小，最小值为2.

三 、构建动态线段与已知线段长度的数量关系

在图形运动的过程中，可以发现动态线段的长度与某已知线段间存在一定的数量关系，再通过作辅助线，引导学生分析它们之间的关系.

四、运用二次函数的性质求最值

如图，在平面直角坐标系中，已知A(2,4)，P(1,0).B为y轴上的动点，以AB为边构造△ABC，使点C在x轴上，∠BAC=90°.M为BC的中点，则PM的最小值为____.

此题有多种解法可以求解，运用二次函数的性质来求解简洁、明了，学生容易想到并能顺利完成.可以用下面这种解法求解：过A作AM⊥y轴，垂足为M,过C作CN⊥AM，垂足为N，设OB=a,OC=b,由△ABM∽△CAN得，b=10-2a,则

当然，用课件解决动态问题的方法远不止这些，但只要课件设计得生动、形象，又能将运动过程呈现出来，教师引导得法，学生的解题能力就能得到很好的培养.

[1]阮忠英.初中几何教学策略浅谈[J].理科爱好者，2009(2)

[2]尚晓青.DGS技术与初中几何教学整合研究[D].重庆：西南大学博士学位论文，2008

G632

B

1008-0333(2017)08-0028-01