对症下药灵动引导——高一数学《三角函数的诱导公式》教学设计

浙江省诸暨市私立诸暨高级中学(311800)

吴 江●

对症下药灵动引导
——高一数学《三角函数的诱导公式》教学设计

浙江省诸暨市私立诸暨高级中学(311800)

吴 江●

本文深入研究了《三角函数的诱导公式》章节的重点内容及要实现的教学目标，并据此探索了该章节的教学设计思路.

《三角函数的诱导公式》；教学设计；高一数学

本课是4组三角函数诱导公式的推导过程及简单应用，基于“诱导公式本质上是圆的旋转对称性和轴对称性的解析表述，即，三角函数的一条性质——对称性，其几何背景是圆的旋转对称性”的角度，理解三角函数诱导公式，引导学生体会数形结合思想和转化思想，培养学生“特殊—一般”的归纳意识，用联系的观点看待问题；让学生经历三角函数诱导公式的推导过程，引导学生学习“怎样研究问题”，学会数学方法，发展数学思维，培养学生科学探究精神.简言之，就是让学生在这节课学习中感受探索发现，学会初步应用，领悟思想方法.

一、复习引入，创设情境

设计意图 自然引入三角函数定义复习，引导学生从“特殊—一般”认知规律，认识单位圆对三角函数定义的简化，为诱导公式的探究学习奠基.

二、思考探究，数形结合

问题1：从现有条件思考，求得三角函数值.这些角和角α有什么关系？三角函数值和角α的三角函数值又有什么关系？

引导学生进行思考探究，课堂交流进行概括归纳.

问题2：如何表示角？此时角的三角函数值和角α的三角函数值有什么关系？

问题4：当角α是第二、三、四象限的角时，上述关系式是否成立？

得出：对于任意角a都有：

类似归纳，引导学生分析下列情形中，角的关系及其三角函数值之间的关系，得出三角函数的诱导公式.

诱导公式1：

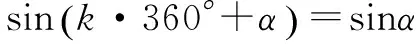
诱导公式2：

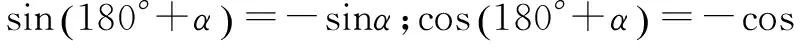
说明：①公式中α是任意角；

②如果α是弧度制，即有：

③公式特点：函数名不变，符号看象限.

诱导公式3：

说明：①公式中α是任意角；

②在弧度制和角度制下，公式均成立；

③公式特点：函数名不变，符号看象限；

诱导公式4：

诱导公式5：

说明：①公式四、五中α是任意角；

②在弧度制和角度制下，公式均成立；

③公式特点：函数名不变，符号看象限；

诱导公式6：

说明：①公式中α是任意角；

②在弧度制和角度制下，公式均成立；

③公式特点：函数名不变，符号看象限.

【设计意图】从两个角的终边关于y轴对称，自然过渡让学生自主探究，应用对称思想去研究三角函数问题，按照“角间关系-对陈关系-坐标关系-三角函数值关系”研究路线，让学生经历三角函数诱导公式的推导研究过程，得出诱导公式，将问题研究一般化.

三、回顾反思，思想升华

问题：怎样获得三角函数的诱导公式？你在研究过程中有什么体会？

前五组诱导公式：函数名不变，符号看象限；

数学思想应用：数形结合，特殊到一般，类比思想，转化化归思想；

两个推导过程：诱导公式推导，求值化简.

【设计意图】在开放式小结中，不同学生有不同收获和体验，结合问题的回答，回顾反思三角函数诱导公式的推导过程和方法，增强学生个体情感体验，总结记忆三角函数诱导公式规律.

G632

B

1008-0333(2017)09-0025-01