一种用于电子式互感器相位补偿的数字移相方法
程含渺,徐 晴,纪 峰,穆小星,陈 刚,田正其,胡 琛(.国家电网公司电能计量重点实验室(国网江苏省电力公司电力科学研究院),江苏南京009;.华中科技大学电气与电子工程学院,湖北武汉430074)
一种用于电子式互感器相位补偿的数字移相方法
程含渺1,徐 晴1,纪 峰1,穆小星1,陈 刚1,田正其1,胡 琛2
(1.国家电网公司电能计量重点实验室(国网江苏省电力公司电力科学研究院),江苏南京210019;2.华中科技大学电气与电子工程学院,湖北武汉430074)
电子式互感器的采集器在采样模拟信号时一般有固定的相位误差,影响了测量准确度,需要使用移相方法校正相位误差。针对数字移相方法,提出了基于最小二乘拟合的数字移相算法,推导出了数字移相递推式,并仿真分析了移相算法的性能。结果表明,该算法均具有较高的移相分辨率和移相精度,且能保证幅值准确度。将该算法应用于基于Rogowski线圈的电子式互感器,准确度比较测试验证了该算法的可行性和有效性。
电子式互感器;相位偏差;数字移相;最小二乘拟合
0 引言
电子式互感器主要由传感器、采集器和合并单元三部分组成,由于其优越的传感性能、绝缘性能和性价比优势而大量应用于智能电网的建设[1-3]。在设计和制造时,由于传感器原理和采集器前端的信号调理电路,采集器输出的采样信号在相位上滞后于实际一次输入信号,所以有必要研究如何对该模拟相位差进行补偿。
目前主要采取2种方法补偿相位差:一种是在采集器中引入模拟移相电路对输入的模拟信号进行移相[4-6],另外一种是在采集器中采用数字移相方法对采集器输出信号进行移相处理[7-10]。模拟移相电路受到了电子元器件长期稳定性的制约,增加的模拟电路环节既增加了采集器的功耗,又容易受到自然环境和电磁环境影响量的干扰,降低了设备的可靠性。近年来,电子式互感器相位差补偿的研究更多地集中在利用数字移相方法来校正相位。文献[7]将模拟移相电路数字化,并采用相位均衡方法实现校正数字移相的非线性相位,运算过程复杂。文献[8]提出了一种短数据窗移相算法,利用3个采样点即可实现移相计算。文献[9,10]以该算法为基础做了更深入的工作,取得了较好的效果。但从短数据窗移相算法推导过程可以看出其准确度与采样率和信号频率有关。文献[11]总结比较了现有的大部分移相算法,其中提到的移点法常见于直接数字频率直接合成(direct digital frequency synthesizer,DDS)技术中,原理简单,但移相分辨率有限,取决于每周波离散点数。文献[12]基于锁相环技术对移点法进行了改进,提高了移相分辨率,但实现过于复杂。总之,目前的数字移相方法较多,但在准确度性能和复杂度方面不能达到很好的平衡。
为了解决上述问题,根据移相原理,提出了一种基于最小二乘法拟合的数字移相算法,已应用到了合并单元校验系统[13]。该算法基于移点的思想,很好地平衡了运算复杂度和移相性能,改善了移相分辨率,降低了计算复杂度。算法的计算量小,易于硬件实现。本文在文献[13]的基础上,更详细深入推导和分析了该移相算法,并将其应用于电子式互感器设计,实际测试结果进一步验证了算法的有效性。
1 基于最小二乘数字移相算法
1.1移相原理
最小二乘法是一种数学优化方法,通过最小化误差的平方和寻找数据的最佳函数匹配。如图1所示,假设被测信号为S,由于互感器自身以及采集器的信号处理部分的影响,信号在时间上滞后Δt,则实际采样信号为相位滞后的信号S′。为了真实还原被测信号,需要将S′向前移相Δt。
假设在ts时刻采样点为A′,可以计算出Δt之前的值为A″,将A″作为ts时刻的采样值A,即实现了将S′向前移相Δt,从而得到真实的被测信号S。
根据上述过程,基于最小二乘拟合移相的原理如下:假设根据电子式互感器的若干点采样值,由最小二乘拟合算法,可以得到S′的局部拟合表达式。
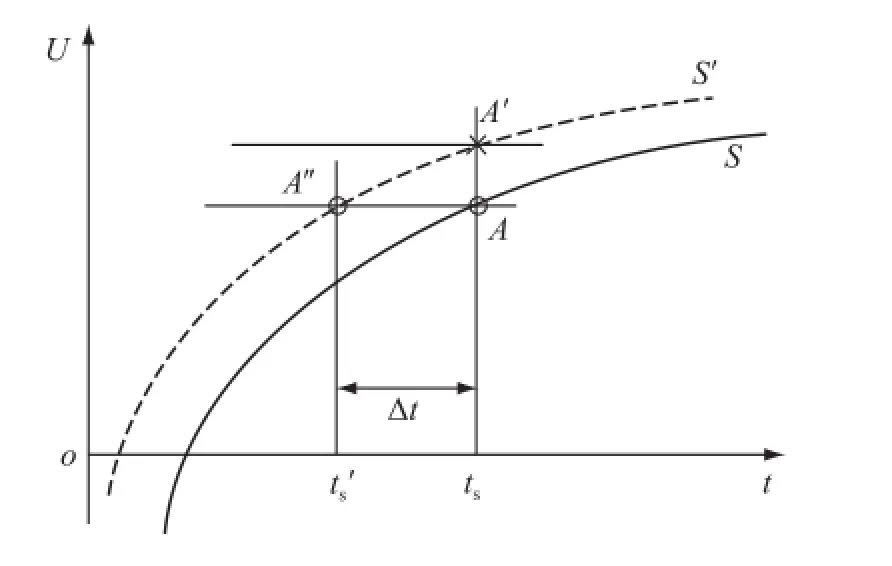
图1 移相示意图Fig.1 Schematic of phase⁃shift
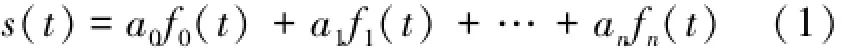
式(1)中:f0(t),f1(t),…,fn(t)为基函数;a0,a1,…,an为基函数的系数。
在ts时刻,A′点的值为:
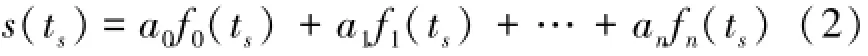
Δt之前A″点的值为:
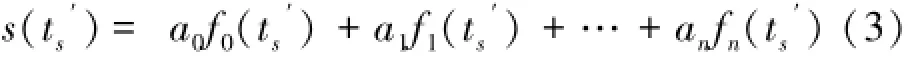
将A″作为ts时刻的采样值,并依次类推。最终可以根据实际的采样点得到向前移相Δt的实际被测信号。
值得注意是,与相位补偿有相似之处的另一种数据处理是同步,2者既有联系也存在区别。同步是指在采样信号能真实表示被测信号情况下,仅仅需要根据采样点获得特定时刻的采样值,也叫重采样。文献[14,15]对插值法数据同步进行了讨论。在图1中,若将A″作为ts′时刻的采样值,实现的则是数据同步。
1.2算法推导
为了实现上述移相,本文推导出一种基于n阶m点多项式最小二乘拟合数字移相公式。(1)n阶多项式拟合函数的基函数为:
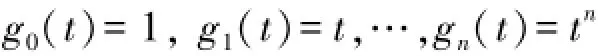
(2)n阶拟合函数为:

(3)假设从t1时刻开始等间隔的m点数据为:g(t1),g(t2),…,g(tm);
(4)由m点数据和拟合曲线函数得到方程组:

(5)令基函数值为矩阵G,系数为向量k,函数值为向量y,即:

则方程组(5)可写成:

在数学上可以证明:
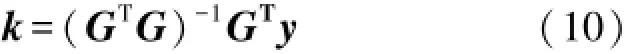
(6)假设g(tm)超前Δt的值为h(tm),则:

(7)将式(10)带入式(11),可得h(tm)和y的关系具有如下形式:
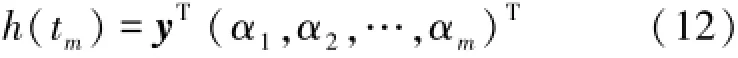
式(12)中的(α1,α2,…,αm)T是仅仅与Δt相关的常数,定义为移相常系数,由下式给出:
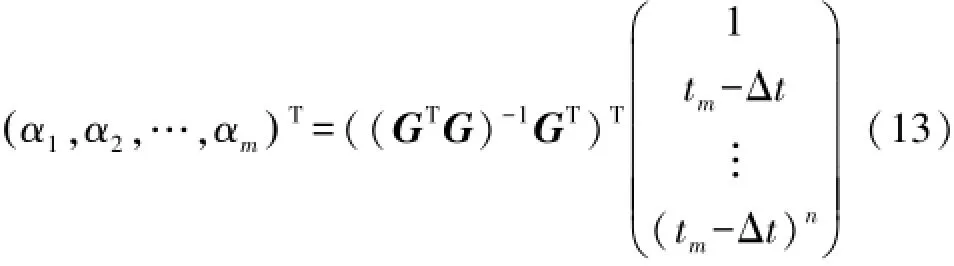
式(13)中的Δt>0时为超前移相;Δt<0时为滞后移相。
该常数在此并无实际的物理意义,只有在设计模拟移相器时才具有物理意义[16]。式(13)的离散归一化形式为:
eout(n)=β1e(n)+β2e(n-1)+…+βme(n-m)(14)式(14)中:eout(n)为根据当前时刻接收的m点采样值求出的移相Δt后的采样值;β1,β2,…,βm为离散归一化移相常系数。
假设采样周期为Ts,离散归一化移相常系数由下式给出:
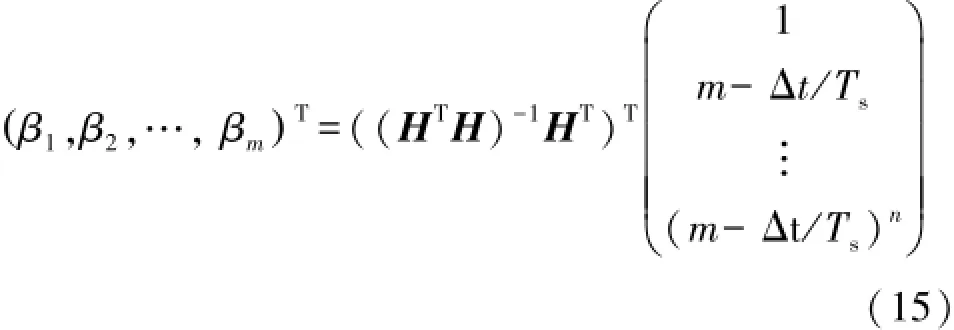
式(15)中对应的矩阵H为:
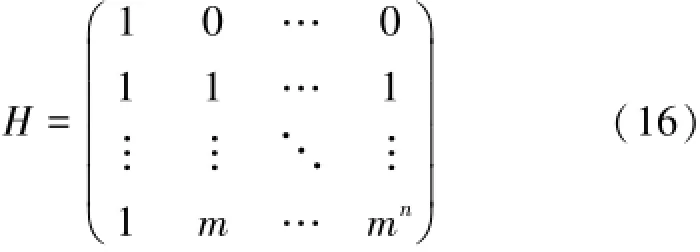
从推导过程可知,该算法的移相分辨率取决于采集器中的微处理器(microcontroller unit,MCU)计算能力,只要MCU计算的有效位数足够多,则理论上移相分辨率Δt的值也将足够小。但实际应用中,MCU的计算能力难免有限,故移相分辨率也将受到限制的,但这并不是算法本身引起的。
1.3算法仿真
为了验证最小二乘拟合数字移相方法的有效性,文献[15]做了简单仿真验证。本文从时域和频域进行了分析。1 μs时间延迟在50 Hz条件下对应1.08′的相位偏差,所以根据式(16)可以计算对应的延迟时间:

式(17)中:θ为相位偏差;Δt为延迟时间。
本文假设输入信号为Vi=sinωt,需要移相的时间分别为前移62.5 μs或者后移62.5 μs,根据式(13),移相的点数分别为前移0.25点和后移0.25点,计算出的延迟常系数如表1所示。
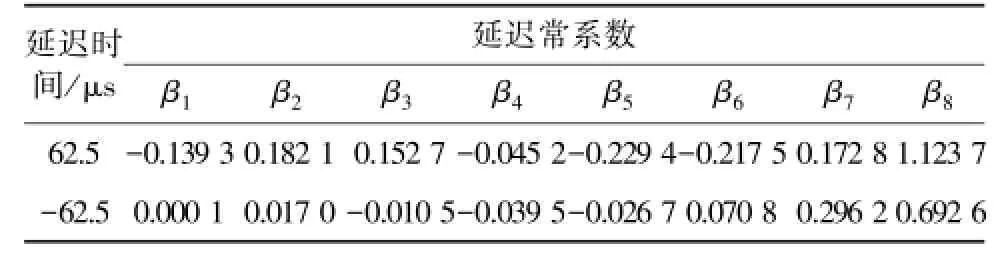
表1 数字移相的延迟常系数Table 1 Delay constant coefficients of digital phase shift
根据表1的计算结果,代入式(12)中,分别仿真计算前移和后移后的输出。归一化后的仿真波形如图2所示。移相前后的相位差和幅值差如表2所示。
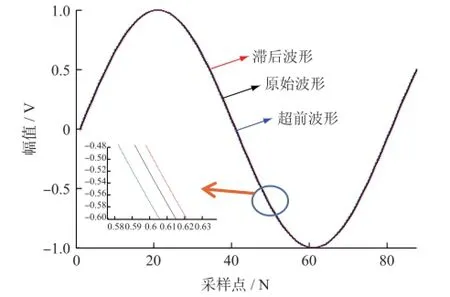
图2 数字移相仿真图Fig.2 Simulation figure of digital phase shift
从仿真结果可以看出,采用三阶8点多项式拟合的数字移相方法,对幅值误差和相位误差都几乎没有影响,具有较高移相准确度。

表2 移相的相位差和幅值差Table 2 Phase errors and ratio errors after phase shift
以上仿真在时域验证了移相效果,下面从频域进一步分析该算法。对式(14)进行变形和z变换,求出其z域传递函数为:
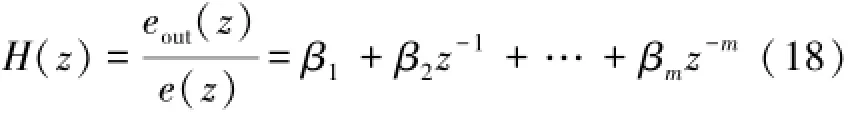
在上述仿真条件下,以前移50 μs为例分析该方法在频率的性能,改变被测信号频率,分析该方法在频率变化时的性能,数字移相的频率仿真特性如图3所示。
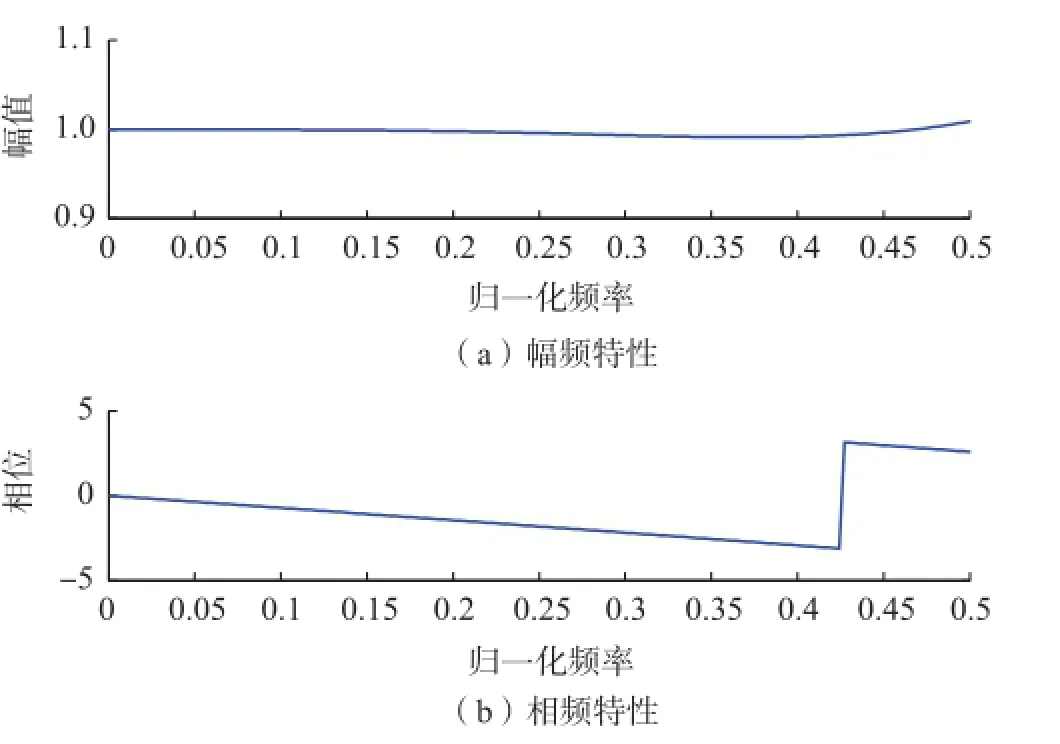
图3 数字移相的频率特性Fig.3 Frequency characteristics of digital phase shift
从图3可以看出,该移相方法在40次谐波以内均具有增益约为1的幅频特性和线性相位,即该算法不会引入幅值误差,群延迟时间也是恒定的,表明即使输入信号含有谐波,本算法也能够实现准确的相位补偿。
2 试验验证
2.1模拟移相电路和数字移相算法的比对试验
本试验的目的在于验证数字移相算法能够实现和模拟移相电路相同的移相效果。具体试验布置图如图4所示。本试验需要使用到2个罗氏线圈(Rogowski线圈,0.2S级准确度),其中1号罗氏线圈输出经过模拟移相电路后输出数字信号给数字信号处理单元,2号罗氏线圈在A/D采样后再进行数字移相,输出数字信号提供给同一个数字信号处理单元,A/D芯片采用的是AD7685。数字信号处理单元比较两路的输出并计算幅值偏差和相位偏差,将结果最终送到计算机(personal computer,PC)中进行显示。本试验采用的罗氏线圈基于印制电路板(printed circuit board,PCB)设计,可以保证良好的一致性。另外需要注意的是,罗氏线圈输出正比于一次电流的微分,为了还原一次信号,需要对罗氏线圈输出进行积分,本试验采用的是改进的AI-Alaoui积分算法,能提高积分器的准确度,并同时改善了数字积分器的抗直流失调量的性能[17]。最终本试验结果如表3所示。
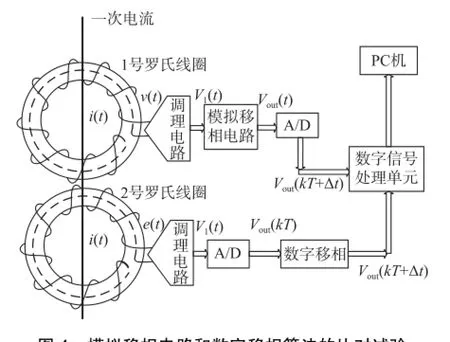
图4 模拟移相电路和数字移相算法的比对试验Fig.4 Comparison test between analogue phase⁃shift circuit and digital phase⁃shift algorithm

表3 比对试验结果Table 3 Results of the comparison test
表3的幅值偏差和相位偏差为2路数字信号的绝对偏差,由结果可知,在额定电流600 A工况下,模拟移相电路和数字移相算法能达到相同的移相效果,不会对幅值造成影响,与此同时,数字移相电路不会受到温度、电磁环境和自然环境等因素的影响。
2.2准确度测试试验
为了进一步验证本算法的准确性,将该算法引入电子式互感器采集器中,进行如图5所示的电子式互感器准确度测试试验。其中,罗氏线圈依然采用第2.1节试验中的线圈,不过其中一路不再加上模拟移相电路。2个罗氏线圈输出经过合并单元(merging unit,MU)后进入电子互感器校验仪。试验中用到的标准互感器为0.02级,变比600 A/5 A的电磁式电流互感器,输出经过一个0.02级,变比为5 A/4 V的标准变换器后进入电子式互感器校验仪。数字输出的电子式互感器校验一般不能采用差值法,而采用绝对测量法,该内容的研究已经非常多[18]。本文采用自行研制的电子式互感器校验仪对上述电流互感器进行准确度测试,该校验仪的准确度等级为0.05级,不确定度分别为f=0.017%和δ=0.6′(k=2),2个罗氏线圈的准确度测量结果如表4和表5所示[19]。
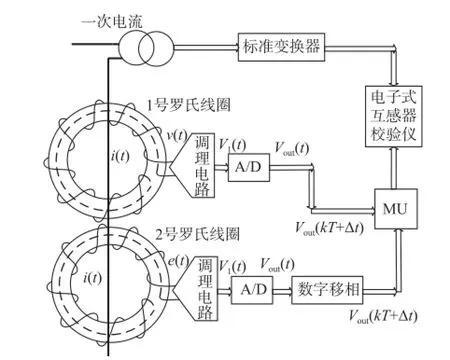
图5 基于数字移相算法的电子式互感器准确度试验Fig.5 Accuracy test of digital phase⁃shift based electronic transformer
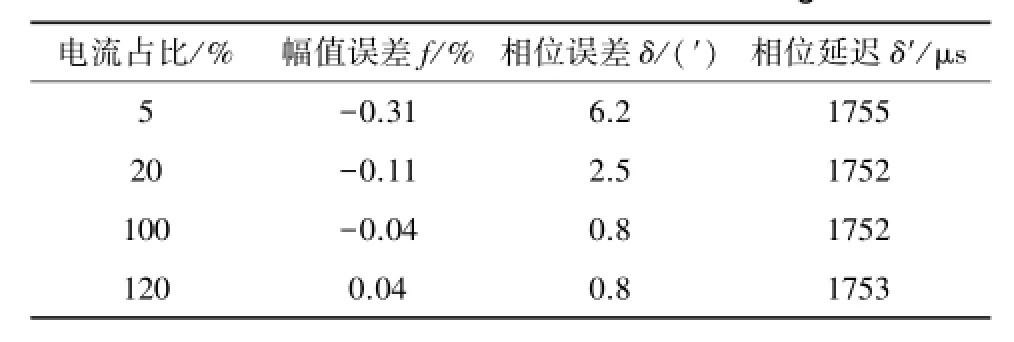
表4 1号罗氏线圈准确度测试结果Table 4 Results of error calibration of 1#Rogowski coil
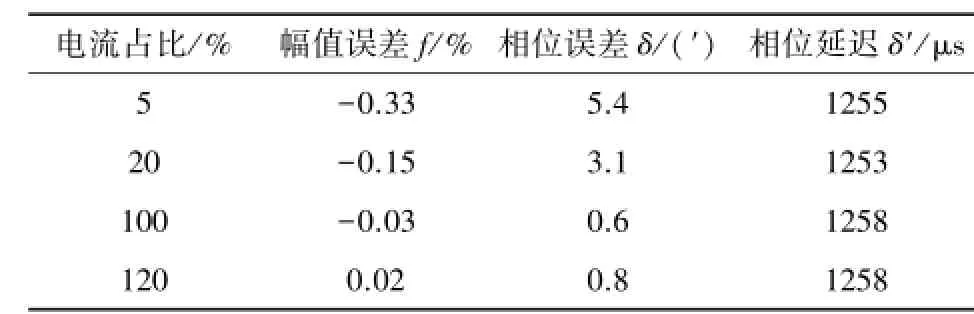
表5 2号罗氏线圈准确度测试结果Table 5 Results of error calibration of 2#Rogowski coil
从表4和表5可以看出,基于最小二乘拟合数字移相算法能校正固定相位差,减小相位延迟,且具有较高的幅值准确度和相位准确度,可用于电子式互感器设计之中,已达到减小电子互感器输出相位差的目的,更好地满足间隔层设备的实时性要求。
3 结语
本文针对电子互感器的传感器和前端模拟信号调理电路引入的相位差,提出了一种基于最小二乘的数字移相方法,推导出了移相公式,仿真和试验结果均表明该方法可以用于电子式互感器中,补偿该部分的相位延迟。和模拟移相电路比较,具有长期稳定性好、抗干扰、功耗低等优点。
(1)该方法不但可用于电子式互感器的数据处理,还可以用于其他需要做数字移相的应用场合,如模拟量输入合并单元等。
(2)本移相方法基于最小二乘拟合,因此对测量波形有一定的平滑作用,但在较大的测量噪声情况下,平滑效果一般。此外,移相算法虽然固然会存在滞后效应,但是这部分算法是一种递推算法,运算复杂度大大降低,一个周波的运算次数是80次乘法和80次加法,和需要补偿的模拟电路延时相比较小。试验结果也表明,移相算法可以很好地补偿模拟电路引入的相位差,有效地减小电子式互感器输出的相位差。
(3)本文仅研究了多项式为基函数的拟合移相,后续可以研究不同基函数的移相效果,并可以研究移相同时能提高信噪比的新算法。
[1]李九虎,须 雷,罗苏南,等.电子式互感器在数字化变电站中的应用[J].江苏电机工程,2007,26(S):44-47.
LIU Jiuhu,XU Lei,LUO Sunan,et al.Application of electronic transformerindigitalsubstation[J].Jiangsu Electrical Engineering,2007,26(S):44-47.
[2]汤汉松,孙志杰,徐大可.数字化变电站的现状与未来[J].江苏电机工程,2007,26(S):5-7.
TANG Hansong,SUN Zhijie,XU Dake.The actuality and future of digital substation[J].Jiangsu Electrical Engineering,2007,26(S):5-7.
[3]秦 冉,王倩倩,杨世海,等.全光纤电流互感器现场运行误差特性研究[J].江苏电机工程,2013,32(2):7-10.
QIN Ran,WANG Qianqian,YANG Shihai,et al.Research on field operation character of fiber current transformer[J].Jiangsu Electrical Engineering,2013,32(2):7-10.
[4]贾春荣,邸志刚,张庆凌,等.电子式电流互感器相位补偿设计[J].电力系统自动化,2007,31(19):76-79.
JIA Chunrong,DI Zhigang,ZHANG Qingling,et al.Phase compensation design of electronic current transducer[J].Auto⁃mation of Electric Power Systems,2007,31(19):76-79.
[5]肖 霞,徐 雁,叶妙元.电子式电压互感器中的相位补偿研究[J].高压电器,2010,46(3):41-44.
XIAO Xia,XU Yan,YE Miaoyuan.Phase compensation scheme for electronic voltage transducer[J].High Voltage Ap⁃paratus,2010,46(3):41-44.
[6]刘家芳,刘霞忠.混合式光电电流互感器相位补偿技术[J].电力自动化设备,2005,25(5):30-33.
LIU Jiafang,LIU Xiazhong.Phase compensation technique for hybrid optoelectronic current transformer[J].Electric Power Automation Equipment,2005,25(5):30-33.
[7]罗 彦,段雄英,邹积岩,等.电子式互感器中数字同步和数字通信技术[J].电力系统自动化,2012,36(9):77-81.
LUO Yan,DUAN Xiongying,ZOU Jiyan,et al.Digital syn⁃chronization and communication technology for electronic trans⁃former[J].Automation of Electric Power Systems,2012,36(9):77-81.
[8]姚争辉,彭红海,周有庆,等.一种短数据窗的移相新算法[J].继电器,1998,26(5):12-13.
YAO Zhenghui,PENG Honghai,ZHOU Youqing,et al.A new phase shift method with short window[J].Relay,1998,26(5):12-13.
[9]朱 超,梅 军,黄 灿,等.测量用电子式互感器的延时补偿设计[J].电力系统自动化,2013,37(21):184-189.
ZHU Chao,MEI Jun,HUANG Can,et al.Delay compensation design for electronic measuring transformer[J].Automation of Electric Power Systems,2013,37(21):184-189.
[10]阳 靖,周有庆,刘 琨.电子式互感器相位补偿方法研究[J].电力自动化设备,2007,27(3):45-48.
YANG Jing,ZHOU Youqing,LIU Kun.Research on phase compensation of electronic transformer[J].Electric Power Au⁃tomation Equipment,2007,27(3):45-48.
[11]朱 鹏,李开成,孙 健,等.电子式互感器相位补偿方法的研究和比较[J].电测与仪表,2014,51(12):7-11.
ZHU Peng,LI Kaicheng,SUN Jian,et al.Research and com⁃parisononphasecompensationschemeforelectronic transformer[J].Electrical Measurement&Instrumentation,2014,51(12):7-11.
[12]李红斌,冯 凯,张 艳,等.光学电流互感器相位误差的分析[J].高电压技术,2004,30(3):15-16.
LI Hongbin,FENG Kai,ZHANG Yan,et al.Analysis on phase error of optical current transformer[J].High Voltage Engineering,2004,30(3):15-16.
[13]程含渺,李红斌,陈 刚,等.模拟量输入合并单元无同步信号校验技术研究[J].高电压技术,2016,42(7):2338-2345.
CHENGHanmiao,LIHongbin,CHENGang,etal. Calibration technique in the absence of synchronization signals for merging units with analogue input[J].High Voltage Engi⁃neering,2016,42(7):2338-2345.
[14]董义华,孙同景,徐炳垠.基于三次样条插值理论的电子式互感器数据同步[J].电力自动化设备,2012,32(5):102-107.
DONGYihua,SUNTongjing,XUBingyin.Data synchronizationbasedoncubicsplineinterpolationfor electronic instrument transformers[J].Electric Power Automa⁃tion Equipment,2012,32(5):102-107.
[15]闫志辉,胡彦民,周丽娟,等.重采样移相技术在过程层IED中的应用[J].电力系统控制与保护,2010,38(6):64-71.
YAN Zhihui,HU Yanmin,ZHOU Lijuan,et al.Application of resample phase shifter technique in process layer IED[J]. Power System Protection and Control,2010,38(6):64-71.
[16]VAINIO O,OVASKA S J.A class of predictive analog filters for sensor signal processing and control instrumentation[J].IEEE Transactions on Industrial Electronics,1997,44(4):565-570.
[17]LUO Pandian,LI Hongbin,LI Zhenhua.Two high accuracy digital integrators for rogowski current transducers[J].Review of Scientific Instruments,2014,85(1).
[18]范 洁,程含渺,季欣荣,等.基于时间数字转换器的数字输出电子式互感器校验系统[J].电力自动化设备,2014,34(10):164-168.
FAN Jie,CHENG Hanmiao,JI Xinrong,et al.TDC⁃based cali⁃bration system of electronic transformer with digital output[J]. Electric Power Automation Equipment,2014,34(10):164-168.
[19]CHENG Hanmiao,LI Hongbin.An improved calibration system with phase correction for electronic transformers with digital out⁃put[J].Review of Scientific Instruments,2015,86(8).
Nanjing 210019,China;2.SEEE Huazhong University of Science and Technology,Wuhan 430074,China)
A Digital Phase⁃shift Method for Phase Compensation of Electronic Instrument Transformers
CHENG Hanmiao1,XU Qing1,JI Feng1,MU Xiaoxing1,CHEN Gang1,TIAN Zhengqi1,HU Chen2
(1.State Grid Key Laboratory of Electrical Power Metering(State Grid Jiangsu Electric Power Company Research Institute),
A fixed phase displacement exists when electronic instrument transformers sample analog signals,which affects the measurement accuray,and needs to be corrected using phase shift method.This paper proposes a digital phase⁃shift method based on least⁃square fitting algorithm.The digital phase shifting recurrence formula is deduced,and the performance of phase shifting algorithm is simulated and analyzed.The results show that the method has a relatively high resolution and precision in phase⁃shifting,furthermore,it can guarantee the amplitude measurement accuracy.The algorithm is applied to the Rogowski coil based electronic instrument transformers,and the feasibility and validity of the algorithm are verified by accuracy comparison test.
electronic instrument transformer;phase displacement;digital phase⁃shift;least⁃square fitting
TM743
:A
:2096-3203(2017)02-0082-06

程含渺
程含渺(1988—),男,湖北汉川人,博士,从事数字电能计量与设备状态监测技术研究工作;
徐 晴(1973—),女,江苏南京人,教授级高级工程师,从事电力计量检测与管理工作;
纪 峰(1981—),男,江苏淮安人,高级工程师,从事电能表实验室检定研究工作;
穆小星(1963—),男,江苏南京人,高级工程师,从事电力计量测试及技术研究工作;
陈 刚(1985—),男,湖北黄梅人,高级工程师,从事用电信息采集技术研究工作;
田正其(1986—),男,江苏南通人,工程师,从事电能表室内检定技术研究工作;
胡 琛(1986—),男,江西南昌人,博士研究生,从事电子式互感器及数字电能计量研究工作。
(编辑 徐林菊)
2016-11-07;
2017-01-09
国家自然科学基金项目(51507091);
国家电网公司科技项目:智能变电站电子式互感器复杂环境下运行性能评估关键技术研究

