适用于有高差线路的覆冰输电导线ANSYS找形方法
谢云云,金 颖,黄琳雁,刘旭斐,王昊昊,郁 琛(.南京理工大学自动化学院,江苏南京009;.中航工业成都飞机工业(集团)有限责任公司,四川成都6007;.云南电力调度控制中心,云南昆明6500;.南京南瑞集团(国网电力科学研究院),江苏南京000)
适用于有高差线路的覆冰输电导线ANSYS找形方法
谢云云1,金 颖2,黄琳雁1,刘旭斐3,王昊昊4,郁 琛4(1.南京理工大学自动化学院,江苏南京210094;2.中航工业成都飞机工业(集团)有限责任公司,四川成都610073;3.云南电力调度控制中心,云南昆明650011;4.南京南瑞集团(国网电力科学研究院),江苏南京210003)
输电线路覆冰会对电网运行产生严重影响,输电导线找形是基于ANSYS对覆冰输电线路进行力学分析的基础。现有ANSYS找形方法主要以跨中弧垂或导线水平应力收敛作为结束条件。对于有高差的输电线路,水平应力和最大弧垂并非在一档中间位置,跨中弧垂或水平应力的确定较为复杂。为此,文中提出基于最低点位置的输电导线找形方法。首先基于解析法求解导线最低点位置,对最低点不在档内的情况需要虚拟出最低点,再通过修改弹性模量的方式使导线位于接近最低点,然后将弹性模量修改为实际值,重复迭代直至导线到达最低点。仿真结果验证了文中方法对不同类型输电导线的有效性。
ANSYS;输电导线;找形;最低点
0 引言
覆冰灾害是电力系统经常受到的自然灾害之一,会对电力系统造成极大的破坏,如2008年我国南方地区极端冰雪灾害,造成直接经济损失逾1100亿元[1-3]。分析输电线路覆冰后的力学特性是输电线路设计、覆冰故障分析、脱冰控制等研究的基础。由于输电导线是悬链线,对输电线路进行力学分析的第一步是模拟出导线的形状,即输电导线找形,导线找形的速度和准确性会影响到后续动力学分析的速度和精度[4]。
输电导线是一个索结构,索结构随着拉力的不同呈现不同的形态,只有在确定形态的基础上才能进行动态分析。索结构的找形是确定索单元在自重或预应力作用下达到的平衡状态[5-7]。索结构具有很强的几何非线性,因ANSYS软件具有较强的非线性处理能力[8],其广泛应用于现有输电线路覆冰动态响应研究中[1,9,10]。
基于ANSYS的输电线路找形方法主要有小弹性模量法和直接迭代法。文献[11-13]中采用了直接迭代法找形,以导线的水平张力为收敛值,对其施加自重荷载,且仅在自重荷载的作用下进行非线性迭代。直接迭代方法设置较为简单,操作方便,但需要大量的迭代次数才能收敛。文献[1,14]利用了预张拉力作用下的初始状态线长与找形后线长相等的原则,采用最低点弧垂设置导线初始形状,再通过自重荷载进行非线性迭代找形。该方法是直接迭代法的改进,迭代次数少,但对两端有高差的情况设置较为复杂。文献[3,4,15-17]采用小弹性模量法进行找形,对直线模型设置比实际值小的弹性模量值,求得导线在自重荷载作用下的初始状态后,再恢复导线的实际弹性模量值进行非线性迭代。小弹性模量法设置较复杂,迭代次数少,但弹性模量值的设置需要多次尝试,可能存在不收敛的情况。上述研究中是通过导线水平应力值或导线弧垂值达到设定值作为迭代收敛的条件,但对两端有高差的输电线路,导线水平应力和弧垂并非在中间点,水平应力值或弧垂值的确定较为复杂。
为此,本文提出了以导线最低点为参考的输电导线ANSYS找形方法。首先基于解析法求出导线最低点的位置,对最低点不在档内的情况虚拟出导线最低点,再修改导线弹性模量使导线最低点接近设定值,再将弹性模量改为实际值,对导线非线性迭代达到最低点,完成找形。最后通过不同类型输电线路仿真验证了本文方法的有效性。
1 基于解析法的最低点计算
由于输电线路2悬挂点距离较大,电线刚度对导线几何形状影响可以忽略,故一般将悬挂导线建模为悬链线模型。根据导线悬链线方法,当坐标原点位于左侧悬挂点时,电线悬链线方程为:

式(1,2)中:x为横坐标;y为纵坐标;σ0为导线水平应力;γ0为电线比载;h为导线两端高差,右侧悬挂点较高时为正;l为档距;Lh=0为两侧悬挂点等高时档内悬链线线长。
通过悬链线方程可以计算得到导线最低点到左侧和右侧悬挂点的距离[18]分别为:

式(3)中:a,b分别为最低点到左侧和右侧悬挂点的距离。
最低点到原点的垂直高度y0为:

式(4)中:β为两悬挂点间的高差角。
通过式(3)和式(4)可以计算得到未覆冰时导线最低点的坐标。在覆冰后,导线上的比载并非只有导线自重,还会有所覆冰的重量。在覆冰前,导线自重单位荷载P0为:

式(5)中:q为电线单位长度的质量。
覆冰后导线的单位荷载Pice为:

式(6)中:b为覆冰厚度;D为电线外径,根据导线型号可以查询到。
因此,覆冰后导线总荷载P1和比载γ1为:

式(7)中:A为导线总截面积,可以根据导线型号查询到。
在输电线路覆冰后,导线水平应力和线长也都会发生变化,覆冰后水平应力可以通过覆冰前后的状态方程求解:
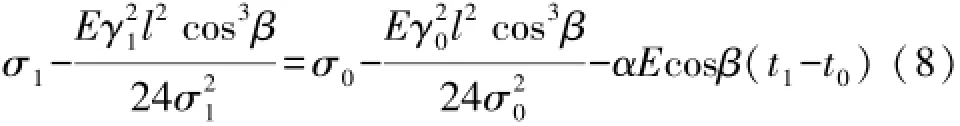
式(8)中:σ1为覆冰导线水平应力;E,α分别为导线的综合弹性系数和温度膨胀系数,可以通过导线型号查询到;t0和t1分别为覆冰前后导线温度。对于连续档导线,可以参考文献[19]中连续档导线的状态方程求取各档导线的水平应力。
覆冰后导线线长为:
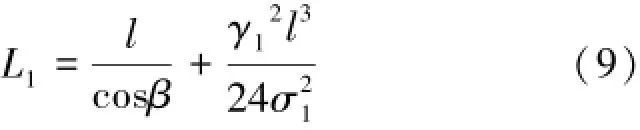
将式(7—9)代入式(3,4),可以得到覆冰后一档有高差输电线路的最低点坐标。
2 基于最低点位置的输电导线找形方法
针对现有ANSYS找形方法在高差输电线路找形时存在的收敛判断较为复杂的问题,且介绍本文提出的以最低点位置为参考的找形方法。
2.1单元设置
基于ANSYS对输电导线进行分析需要将导线离散成有限个单元,对每个单元建立合适的单元模型,才能实现输电导线的找形。由于输电导线具有只能受拉、不能受压的特点,离散后的每个单元的模型需要能够模拟该特点。目前最为常用的单位模型为LINK10单元,该单元是两节点三维杆单元,具有的双线性刚度矩阵特性使其能够模拟轴向仅受拉或仅受压杆单元,将其设为只受拉状态时,如果单元受压,刚度就会消失,从而用其模拟导线状态具有较高的准确性。
2.2找形方法实现
本文输电导线找形方法主要分为3个步骤:悬挂点和参考点的设置,调整弹性模量使导线最低点接近参考点,恢复弹性模型迭代实现精确找形。
(1)悬挂点和参考点设置。当输电线路存在高差时,输电导线的最低点位置可以存在与档内或档外,如图1所示。图1中,A为左悬挂点,B为右悬挂点,O为最低点。对最低点在档内的情况,悬挂点和最低参考点为上面所述。但对最低点不在档内的情况,需要将最低点虚拟为悬挂点,采用较低的悬挂点作为参考,在找形结束后再还原悬挂点。参考点采用式(3)和式(4)可以计算得到。
(2)弹性模量设置。通过查看迭代求解后的Y轴方向的位移形变图,适当调整弹性模量值,使得非线性迭代后的输电导线模型经过预先找好的最低点。弹性模量是一种表示材料发生弹性形变难易程度的指标:弹性模量值越大,材料越难发生弹性形变;弹性模量值越小,材料越容易发生弹性形变。因此,非线性求解后,当最低点出现在的输电导线的弧线模型内时,说明弹性形变不够大,则应适当减小弹性模量值;当最低点出现在的输电导线的弧线模型外时,说明弹性形变过大,则应适当增加弹性模量值。

图1 输电导线的两种形态Fig.1 Two forms of transmission lines
(3)恢复弹性模量后迭代。通过弹性模量设置使导线最低点接近参考点时,将弹性模量恢复为实际值,对施加初始应变进行迭代计算,直至最低点与参考点重合。这一步所需的迭代次数比直接迭代法大为减少,加快了找形的速度。
详细的找形步骤如图2所示。
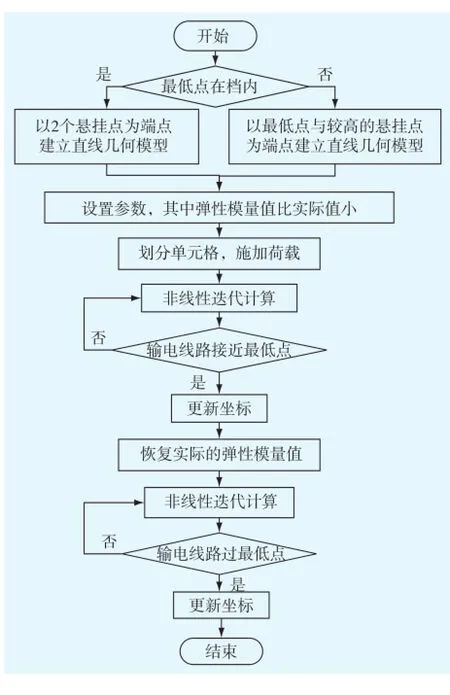
图2 找形流程Fig.2 The flow chart to find the form of transmission line
3 仿真分析
3.1仿真场景
为了说明本文方法的有效性,本文以LGJ300-40型导线为例,构建最低点位于档内和档外输电线路模型,分析本文方法找形结果与其他找形方法及理论值的误差。LGJ300-40型导线的详细参数如表1所示。
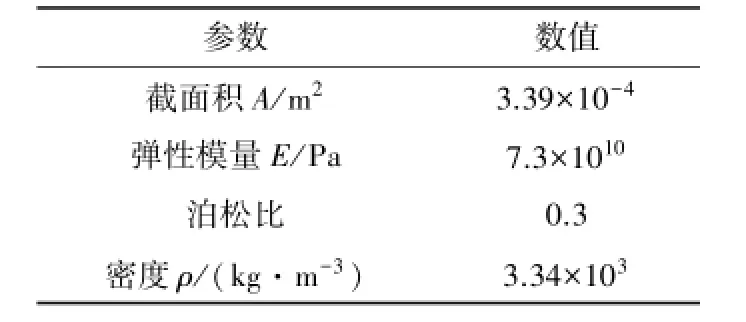
表1 导线参数Table 1 Parameters of the conductor
根据输电导线最低点的位置分布情况,对3种场景进行仿真。场景1,最低点位于档中间,无高差;场景2,最低点位于档内,有高差;场景3,最低点位于档外,具体参数如表2所示。从表2中可以看出第一个场景中最低点位于档距中央,第二个场景最低点位于档内靠近左侧悬挂点的位置,第三个场景最低点位于档外,左侧悬挂点外侧。

表2 场景设置Table 2 Scenarios setting
3.2找形方法有效性分析
3.2.1 结果精度分析。
采用本文提出的找形方法、直接迭代法、小弹性模量法对不同场景输电导线进行找形。针对对后续动态分析有影响的参数,如跨中弧垂、悬挂点应力等,不同找形方法得到的参数结果如表3所示。
从表3中可以看出,3种方法的线长误差曲线的发展趋势一致,随着高差的增加,虽然3种方法的线长误差的绝对值增加了,但误差的百分比反而减小,且最大线长误差也没有超过0.30%;在跨中弧垂和悬挂点应力方面,过最低点法的误差变化最稳定,但是直接迭代法和小弹性模量法的误差有随着高差的增加而增加的趋势。总体来讲,直接迭代法、小弹性模量法和过最低点法的精度没有太大的差别。本文方法的找形结果的精度能够满足要求。
3.2.2 操作复杂度分析
由于场景3中导线最低点不在档内,故采用该场景说明本文方法在操作复杂度方面的优势。场景3下直接迭代法、小弹性模量法和本文方法的找形结果如图3—5所示。

表3 不同场景输电线路找形结果Table 3 The form⁃finding results calculated in difference scenario

图3 直接迭代法的找形结果Fig.3 The form⁃finding result of the direct iteration method
从图3—5中可以看出,图3和图4中不存在最低点,故难以确定水平应力,较为可行的方法是取跨中弧垂达到预设值作为结束条件。但在选取跨中弧垂的操作中,每次迭代完成后,需要首先找出跨中点,然后作垂直线,测量跨中弧垂高度并判断是否达到结束条件。本文方法结果如图5所示,首先计算出最低点位置,然后在最低点与较高的悬挂点之间画出初始导线,在后续找形中,当导线达到实际较低悬挂点时即结束找形,故找形操作简单而方便。从迭代次数中也可以看出,直接迭代法需要30次迭代,小弹性模量法需要8次迭代,而本文方法仅需5次迭代,并且本文方法无需每次迭代后取跨中弧垂,故能够有效减少找形操作的时间。

图4 小弹性模量法的找形结果Fig.4 The form⁃finding result of the small elastic modulus method
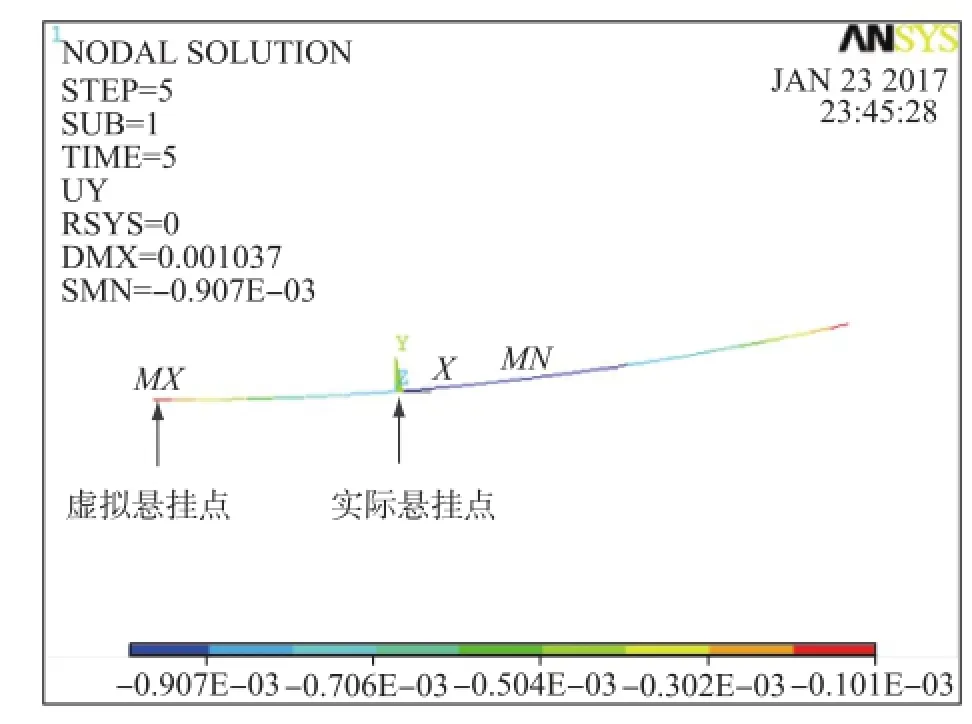
图5 本文方法的找形结果Fig.5 The form⁃finding result of the method in this paper
4 结语
输电线路找形是使用ANSYS软件对输电线路进行动态分析的基础,本文针对现有找形方法在有高差输电线路找形时收敛结束判断较为复杂的问题,提出以导线最低点为参考的找形方法。对最低点不在档内的情况,将最低点虚拟为悬挂点,通过原悬挂点作为参考点。以不同高差的导线为例,对比了本文方法与现有方法的误差,结果表明本文方法与现有找形方法均能满足工程要求,但本文方法具有较为直观的收敛参考,操作更为方便,减少找形的操作时间。
[1]LECOMTE E L,PANG A W,RUSSELL J W.Ice storm 98[M].Canada:Institute for Catastrophic Loss Reduction,1998:62-84.
[2]薛禹胜,费圣英,卜凡强.极端外部灾害中的停电防御系统构思(一)新的挑战与反思[J].电力系统自动化,2008,32(9):1-6.
XUE Yusheng,FEI Shengying,BU Fanqiang.Upgrading the blackout defense scheme against extreme disasters:PartⅠnew challenges and reflection[J].Automatic of Electric Power Sys⁃tems,2008,32(9):1-6.
[3]谢云云,薛禹胜,文福拴,等.冰灾对输电线故障率影响的时空评估[J].电力系统自动化,2013,37(18):32-41.
XIE Yunyun,XUE Yusheng,WEN Fushuan,et al.Space time evaluation of impact of ice disaster on transmission line fault probability[J].Automatic of Electric Power Systems,2013,37(18):32-41.
[4]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007:6-7,172-182.
WANG Xinmin.ANSYS numerical analysis of engineering struc⁃tures[M].Beijing:China Communications Press,2007:6-7,172-182.
[5]JIA Y Z,LIU R P.Form⁃finding system for overhead transmis⁃sion line based on ANSYS[J].2012 International Conference on Future Electrical Power and Energy Systems,2012(17):975-982.
[6]VEENENDAAL D,BLOCK P.An Overview and comparison of structural form finding methods for general networks[J].Inter⁃national Journal of Solids and Structures,2012(49):3741-3753.
[7]MALERBA P G,PATELLI M,QUAGLIAROLI M.An extended force density method for the form finding of cable sys⁃temswithnewforms[J].StructuralEngineeringand Mechanics,2012,42(2):191-210.
[8]陶颐格,刘锐鹏,陈小平.基于ANSYS的架空线找形系统研究[J].广东电力,2011,24(4):64-67.
TAO Jige,LIU Ruipeng,CHEN Xiaoping.Research on the form⁃finding of aerial conductors based on ANSYS[J].Guang⁃dong Electric Power,2011,24(4):64-67.
[9]PAULETTI R,PIMENTA P.The natural force density method for the shape finding of taut structures[J].Computer Methods in Applied Mechanics and Engineering,2008(197):4419-4428.
[10]李 兵,宫鹏涵.ANSYS14有限元分析自学手册[M].北京:人民邮电出版社,2013:160-220.
LI Bing,GONG Penghan.ANSYS14 finite element analysis of self⁃study manual[M].Beijing:Posts&Telecom Press,2013:160-220.
[11]张旺海,于建斌.基于ANSYS的架空输电导线找形研究[J].电力建设,2012,33(2):32-35.
ZHANG Wanghai,YU Jianbin.Research on form⁃finding of aerial lines based on ANSYS[J].Electric Power Construction,2012,33(2):32-35.
[12]孔 伟,朱明伟,付 豪.架空输电线路导线在ANSYS中的找形分析[J].东北电力大学学报,2011(S):64-67.
KONG Wei,ZHU Mingwei,FU Hao.Form finding analysis of overhead transmission lines in ANSYS[J].Journal of Northeast Dianli University,2011(S):64-67.
[13]陈仕良,曹枚根.有限元在架空输电线路导线地线找形分析的应用[J].江西电力,2007,31(6):7-15.
CHEN Shiliang,CAO Meigen.Application of finite element method in form⁃finding analysis of transmission lines[J]. Jiangxi Electric Power,2007,31(6):7-15.
[14]鲁元兵,楼文娟,李焕龙.输电导线不均匀脱冰的全过程模拟分析[J].振动与冲击,2010,29(9):47-50.
LU Yuanbin,LOU Wenjuan,LI Huanlong.Simulation and analysis of the uneven removal of transmission lines[J]. Journal of Vibration and Shock,2010,29(9):47-50.
[15]贾玉琢,刘锐鹏,李正琪.覆冰输电架空导线初始构形研究[J].水电能源科学,2011,29(1):148-150.
JIA Yuzhuo,LIU Ruipeng,LI Zhengqi.Research on initial configuration of iced transmission lines[J].Water Resources and Power,2011,29(1):148-150.
[16]孟遂民,单鲁平.输电线动力学分析中的找形研究[J].电网与清洁能源,2009,25(10):43-47.
MENG Suimin,SHAN Luping.Research on form⁃finding in dynamic analysis of transmission lines[J].Power System and Clean Energy,2009,25(10):43-47.
[17]杨 钦,李承铭.ANSYS索结构找形及悬链线的模拟[J].土木建筑工程信息技术,2010,02(4):61-65.
YANG Qin,LI Chengming.Form⁃finding of cable and simula⁃tion of catenary by ANSYS[J].Journal of Information Technol⁃ogy in Civil Engineering and Architecture,2010,02(4):61-65.
[18]张殿生.电力工程高压送电线路设计手册[M].2版.北京:中国电力出版社,2002:321-324.
ZHANG Diansheng.High Voltage Power Transmission Line Design Manual for Power Engineering[M].2nd ed.Beijing:China Power Press,2002:321-324.
[19]邵天晓.架空送电线路的电线力学计算[M].2版.北京:中国电力出版社,2003:180-183.
SHAOTianxiao.Mechanicalcalculationofoverhead transmission lines[M].2nd ed.Beijing:China Power Press,2003:180-183.
Form⁃finding Method of Transmission Lines Consulting the Lowest Point
XIE Yunyun1,JIN Ying2,HUANG Linyan1,LIU Xufei3,WANG Haohao4,YU Chen4
(1.School of Automation,Nanjing University of Science and Technology,Nanjing 210094,China;
2.AVIC Chengdu aircraft industry(Group)Co.,Ltd,Chengdu 610073,China;
3.State Grid Yunnan Electric Power Company Dispatch and Control Center,Kunming 650011,China;
4.NARI Group Corporation,Nanjing 210003,China)
Ice covering on the transmission line has great impact on power system security.Form⁃finding of transmission line is the basis for mechanical analysis of iced transmission line by ANSYS.Current form⁃finding methods end with the convergence of sag or the horizontal stress,which is hard to obtain in transmission lines with height difference while the maximum sag isn't in the center position.Therefore,this paper presented a form⁃finding method of transmission lines consulting the lowest point. The method obtained the lowest point by analytic method first,then modified the elastic modulus for coming near the lowest point,and repeated the iteration until the line reaches the lowest point after changing the elastic modulus back to actual value. Simulation results show the effectiveness of the proposed method for different types of transmission lines.
ANSYS;transmission lines;form⁃finding;the lowest point
TM73
:A
:2096-3203(2017)02-0009-05

谢云云
谢云云(1985—),男,江苏南通人,博士,研究方向为电力系统防灾减灾与可靠供电;
金 颖(1989—),女,四川成都人,硕士,研究方向为可靠性分析;
黄琳雁(1992—),女,江苏南通人,硕士研究生,研究方向为电力系统防灾减灾与可靠供电;
刘旭斐(1981—),男,云南昆明人,高级工程师,研究方向为电力系统电网调度;
王昊昊(1979—),男,江苏扬州人,高级工程师,研究方向为新能源并网控制技术、电力系统防灾减灾;
郁 琛(1985—),男,江苏苏州人,博士,研究方向为新能源并网控制技术、电力系统防灾减灾。
(编辑 徐林菊)
2017-01-30;
2017-02-15
国家自然科学基金项目(51507080,61673213);江苏省博士后基金资助项目(1402042C)

