增设 素材分析算理加深理解提高能力
——“一个数除以分数”教学实录与评析
◇执教/马凤娟 评析/陈庆宪
一、提供联系素材,自主探究算理
1.回顾数量关系,自主沟通联系。
呈现以下两个问题和学习要求:
问题①:小明2小时行了6千米,小明平均每小时行多少千米?
学习要求:①写出这两个问题的算式。②说一说你是用什么数量关系写出算式的。
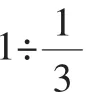
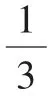
生:是3千米。
学生独立画图思考后,教师让两位学生把图画到黑板上。
生:先画了一段表示1千米,再把这一线段向右延长相等的两段,在整条线段上打上“?km”表示1小时行的路程(如图1)。

图1

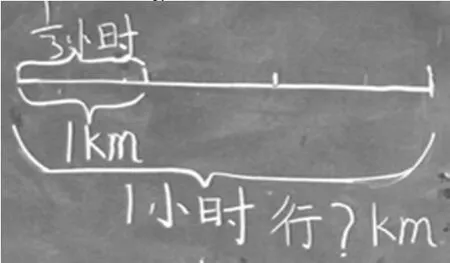
图2
教师根据学生的回答,并结合图把计算过程进行了板书。黑板上呈现了两个算式的计算过程:
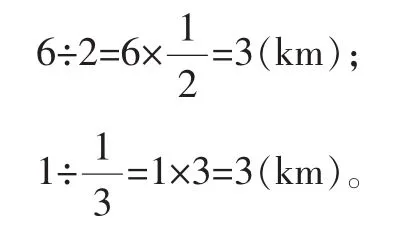
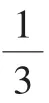
2.继续呈现问题,列式画图说理。
学习要求:(1)列出问题③的算式,想一想这个算式应该怎样计算。(2)画出线段图说明算式和计算过程的意思。
在学生独立思考、小组交流后,教师让一位学生把图画到黑板上(如图3)。针对学生写出的算式和画出的图,组织交流。
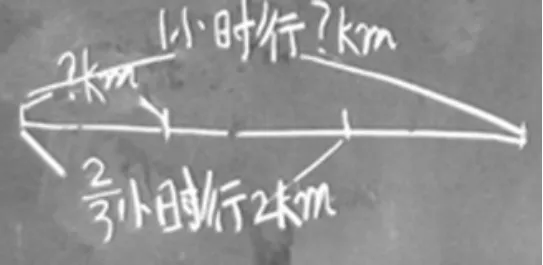
图3
师:你是根据什么写出除法算式的?
生:我是根据“路程÷时间=速度”的数量关系写出算式的。
师:你能不能根据乘法的意义写出算式呢?
师:你能结合自己所画的图说一说计算的过程吗?
3.继续呈现问题,列式看图说理。
学习要求:(1)根据问题④写出算式,想一想应该怎样计算。(2)图4是根据题意画出的,你能根据图4说一说自己的计算过程吗?
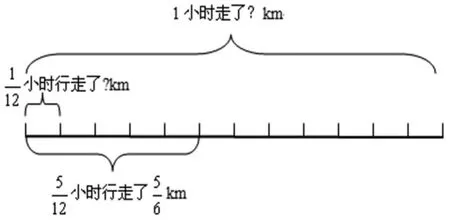
图4
在学生独立思考、互相交流后,再组织学生汇报,并逐步板书如下计算过程:
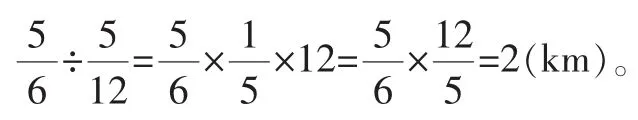
评析:问题③让学生独立列式、画图、说理;问题④让学生先独立列式、观察线段图,再说理。在每个问题解答完成后,教师并没有刻意地去总结“一个数除以分数”的计算方法,目的是为了让学生把更多的注意力放到对算理的理解上。
二、整体观察算式,概括计算方法
教师指着黑板上已形成的四个算式向学生提出:我们上一节课学过“分数除以整数”,请大家仔细观察这些算式,今天我们学习的是——
生:今天我们学习的是“整数除以分数”和“分数除以分数”。
师:概括起来说是“一个数除以分数”。
接着教师提出:请大家观察这些算式的计算过程,你能发现什么?学生独立观察、思考后,在小组里互相交流,然后教师组织总结概括。
生:我发现一个数除以分数等于乘这个分数的倒数。
师:今天我们学习的除法是把除法转化成……
生:把除法转化成乘法。
师:在转化成乘法时要注意什么呢?
生:要把除数变成它的倒数。
这时教师让学生针对黑板上的算式,随机勾画出计算过程的变化,并突出转化过程。
评析:让学生整体观察四个算式去概括计算方法有两点好处,一是体现了从特殊到一般的概括过程,说明计算方法的广义性;二是体验到自己发现计算方法的成功感,进一步激发学习的积极性。另外教师在组织学生观察概括时有意识地突出转化思想,使学生感受到把新知转化成旧知的过程。
三、增设素材解读,加深理解算理
投影逐一呈现以下素材,让学生针对图和算式自主解读意义。
素材一:如图5,这块地中的阴影部分是6公顷,请仔细观察图和每一步的思考过程,先把空格填完整,再说一说:除法算式是怎样推出来的?这个除法算式表示的实际意义是什么?计算过程和结果的实际意义是什么?
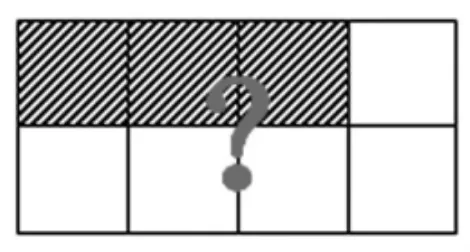
图5
学生观察思考后,教师组织汇报、交流。(略)
素材二:仔细观察图6,先把括号内的数填完整,再说一说:除法式子是怎样推出来的?它表示的实际意义是什么?计算过程每一步的实际意义是什么?
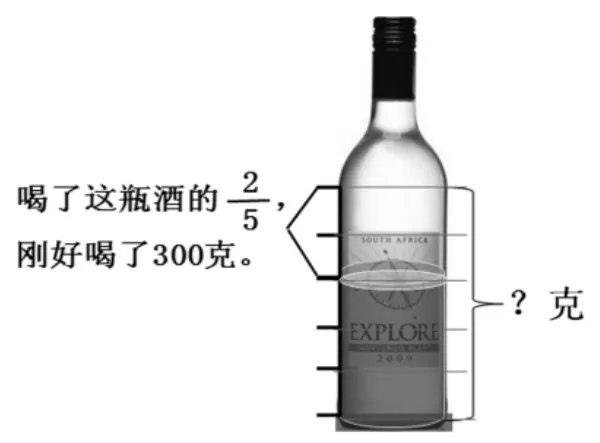
图6

学生独立思考、填空后,教师再组织汇报交流。(略)
评析:我们增设这两个思考素材,其目的有两个:一是让学生进一步理解除法的实际意义,进一步领悟到在什么情况下用除法来解决问题,知道分数除法是从乘法的数量关系中推导而来的,为今后用除法解决分数问题打下了基础。二是为了加深学生对算理的理解,学生针对不同背景解读每步计算过程的实际意义,使学生把算理再次上升为图像表征。
四、精选练习素材,巩固计算方法
1.通过填空、观察,完善计算方法。
填一填。填上适当的运算符号和数。
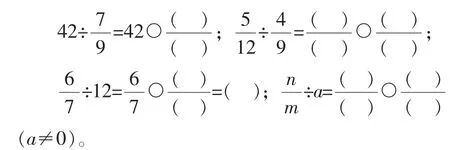
学生独立填空后,再组织反馈交流。(略)
师:今天我们学习了一个数除以分数,上一节课我们学习的是一个数除以整数。通过以上填空和黑板上的这些算式,我们是否可以概括出除以一个数等于什么?
生:等于乘这个数的倒数。
师:那最后一道题提醒我们要注意什么?
生:要注意除以一个不等于0的数。
师:那我们刚才概括的除法计算方法,应该怎样说更完善呢?
学生交流后,教师板书:除以一个不等于0的数,等于乘这个数的倒数。
2.独立算一算教科书(人教版教材六年级上册)第32页第2题的算一算。

学生计算后及时反馈订正。(过程略)
评析:当学生概括出了一个数除以分数的计算方法后,如果按此方法进行计算是很容易的。因为除了把除法转化为乘法,其他都是原有的技能,所以我们在本课对于纯计算的练习没有过多地安排,只给学生精选了以上四个算式的填空和选自教科书中的四个算式。设计这组填空题的目的是让学生进一步概括计算方法,尤其让学生通过对第1题的最后一小题字母的填空,引导学生注意除数仍然不能是“0”,使计算方法的表述更加完善。
五、适当拓展素材,激发学习兴趣
紧接着教师在屏幕上呈现以下一组算式,并向学生提出:有人通过下面的方法也推出了一个数除以分数的计算方法,你能看懂他用了什么规律把除以一个数转化成乘这个数的倒数吗?

学生通过观察思考后说到:以上是利用了商不变的规律推出来的。也就是:被除数和除数乘同一个不为0的数,它的商是不变的。
师:乘同一个数,这个数是从哪里找出来的?
学生再次观察发现,并说出:乘同一个数,这个数是原来除数的倒数。
师:为什么?
生:同乘除数的倒数就可以把除数转化成“1”了。
师:同学们真棒!又看出了把除法转化成乘法的另一种推理方法。今天我们学习的主要是通过数量关系和画图分析来探究出“一个数除以分数等于乘这个分数的倒数”。实际上除了这两种方法,还有其他的推理方法,有兴趣的同学可以在课后继续查一查相关资料。
评析:以上这两个除法算式,就是第一环节中教材例题上的两个除法式子。教师在屏幕上直接呈现推理过程,让学生自己观察、解读,使学生认识到这又是一种把除法转化为乘法的推理方法,而这种推理方法的关键点是把除数转化为“1”。接着教师引导学生回顾本课所采用的推理方法是通过数量关系的分析,以及结合分数的意义把除法转化为乘法的。当然这一环节的拓展性素材要根据教学实际情况灵活处理,由于本课马老师的教学时间有点充裕,所以提供这样的素材,起到很好的拓展推理作用,进一步激发学习兴趣的作用。


