基于Spark Streaming流回归的煤矿瓦斯浓度实时预测*

吴海波 ， 施式亮 ， 念其锋

(1.中南大学 资源与安全工程学院, 湖南 长沙 410083；2.湖南科技大学 计算机科学与工程学院，湖南 湘潭 411201；3.湖南科技大学 资源环境与安全工程学院，湖南 湘潭 411201；4.湖南科技大学煤炭资源清洁利用与矿山环境保护湖南省 重点实验室，湖南 湘潭 411201)

0 引言

对煤矿井下瓦斯浓度进行精确测量和实时监测控制是防止煤矿瓦斯爆炸、确保人身安全的重要措施[1]。为了防治瓦斯灾害，煤矿要求安装瓦斯监测监控系统以提供与瓦斯灾害相关的各种实时环境数据。有效的分析和利用瓦斯监测监控数据，对煤矿关键测点的瓦斯浓度进行预测，使瓦斯灾害的预防和预警成为减少煤矿瓦斯灾害的关键。而传感技术的发展使得煤矿瓦斯监测监控系统采集到的瓦斯监测数据呈现流式大数据的特征，海量的瓦斯监测监控数据通过网络以流的形式传输到煤矿安全监测监控系统中，分析、研究煤矿瓦斯监测监控流数据也成为实时数据流分析问题，流数据具备数据量大、数据实时性价值高等特点，这给煤矿瓦斯浓度预测带来了新的挑战。

目前预测瓦斯浓度的方法既有包括基于时间序列分析[2, 3]、混沌时间序列预测[4]的，也有基于机器学习的支持向量机[5-7]、聚类[8]和基于粒子群优化或遗传算法来优化神经网络[9-12]等，基于机器学习应用于瓦斯浓度预测研究主要关注点在于利用已有的瓦斯浓度数据来进行训练迭代，从而找到最优模型。但机器学习在大数据迭代运算、交互式查询和流式处理上呈现出低效率的问题，导致数据建模时间长、模型更新慢等问题，使得瓦斯浓度数据的预测达不到实时处理的要求。从已有的煤矿瓦斯浓度预测方法来看，瓦斯监测数据从采样、建模、预测的时间跨度为数分钟到数十分钟之间，即预测模型的更新周期至少为分钟级。物联网及分布式并行大数据处理技术的发展使得流数据处理能力得以提升，通过分布式流处理技术可以在大数据下并行快速数据建模，达到流式数据实时处理要求。Spark Streaming流处理技术是Spark核心应用的一个扩展，主要负责处理实时数据流，数据流包括日志、交易数据、传感器数据等。利用Spark Streaming的流处理技术，能保证瓦斯浓度预测模型的实时学习能力，让学习模型随着新的数据流不断更新，使得瓦斯浓度数据处理时间达到实时数据流的时间跨度数百毫秒到数秒之间，从而减少重新计算的开销，能使预测模型更新周期达到秒级，既能提高预测精度，又能满足实时预警要求。

1 Spark Streaming

Apache Spark是基于内存计算的分布式开源集群计算系统。由于利用内存来保存基于MapReduce算法过程的中间输出和结果，这对于交互式数据挖掘和机器学习方法中使用频率较高的迭代计算而言大大提升了工作效率[13]。Spark Streaming作为Spark支持流数据实时处理的组件，是采用将流数据分解成一系列批处理作业来进行流式计算的。Spark Streaming流系统如图1所示。

图1 Spark Streaming流系统示意[14]Fig.1 Overview of the Spark Streaming system[14]

Spark Streaming将输入流数据转化成离散数据流DStream(Discretized Stream)，通过Spark核心引擎，可将每个批次的DStream转换成Spark中的弹性分布式数据集RDD(Resilient Distributed Dataset)，这样，可以通过RDD的转换和行动操作来实现流处理业务的要求。由于Spark还提供可扩展的机器学习库MLlib，Spark Streaming可以通过MLlib对从DStream转换的RDD数据进行分析与建模，从而进行机器学习和应用。

2 瓦斯浓度预测模型

流数据挖掘是指实时的对数据流进行分析并挖掘流数据的信息和模式。为了进行流数据的挖掘，许多机器学习算法和技术被重新设计以适用于流数据。线性回归属于机器学习算法中的监督学习，主要是通过建立线性回归方程来分析一个或多个自变量与因变量关系。线性回归模型简单有效，非常适用于大数据流的建模和预测[15]。

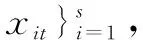
(1)

由公式(1)来预测t+1时刻瓦斯浓度数据。其中，α,β为回归系数，而为白噪声。通过求解回归系数α,β，就可根据一定时期的历史数据来预测y的值。最优回归系数值应使损失函数达到最小来求得，损失函数可定义为预测值与真实值y之差的平方和：

(2)

由公式(2)求解α,β可采用最小二乘法或梯度下降法，Spark Streaming流回归采用的是随机梯度下降算法来求回归系数，当样本数据集n较大时，使用随机梯度下降算法可减少运算复杂度。

3 基于Spark Streaming流回归的瓦斯浓度预测系统

生成由线性回归算法实现的瓦斯浓度预测模型，就必须给定训练数据集，训练数据集可以是监测监控中已保存的历史记录数据，也可以为实时流数据。来自监控监测的实时训练数据集的改变导致预测模型的更新。监测监控数据具有流数据的特点，数据量大导致建模时间长，数据的实时性意味着数据存储时间越长，利用价值越低。因此，传统的利用写入磁盘的历史记录来进行建模方法满足不了在流数据上瓦斯浓度实时预测的要求。为了在瓦斯浓度数据流上进行预测建模，采用分布式流处理框架Spark Streaming来构建基于流回归的瓦斯浓度实时预测系统，Spark Streaming中的DStream可同时进行流数据处理和批处理，满足数据集提取、机器学习模型的训练及模型应用等多种处理类型要求。既能满足大数据处理要求，又能达到流计算的标准。

基于Spark Streaming流回归的瓦斯浓度实时预测系统如图2所示。煤矿瓦斯及相关传感器将监控实时数据通过网络以流的方式传送至流回归系统，数据流可写入分布式存储系统HDFS进行存储，也可直接以流的形式发送至Spark Streaming。存储的数据与实时数据可以结合并通过Spark MLIib来建立流回归模型。流回归模型可随着数据流动态更新，生成回归模型通过Spark Streaming流回归预测算法来进行瓦斯浓度实时预测。

图2 Spark Streaming流回归预测系统Fig.2 Prediction system based on Spark Streaming linear regression

瓦斯浓度流回归预测是将瓦斯监控源产生的实时数据通过流产生器发送到Spark Streaming中，在Spark Streaming流处理中，瓦斯监测数据流会抽象成原始DStream，原始DSteam会将连续的流数据切分成指定时间片的数据RDD。为实现瓦斯浓度预测建模与分析，Spark Streaming提供基于滑动窗口的流计算，利用时间窗口来切分原始DStream，如图3所示。基于窗口长度的RDD是流回归预测模型的基本单元，通过窗口长度的流数据来建立流回归预测模型，而窗口长度可以根据流数据的速率和建模复杂度来确定，尽管Spark Streaming可支持毫秒级建模运算，但在实际实用中，为保证模型的稳定性和预测精度，可将窗口长度设置为1 min或3 min。窗口的滑动距离则用于指定预测模型训练数据的更新长度，同时也指定了模型的更新率。Spark Streaming流计算可将窗口的更新速率达到秒级以满足实时流处理要求。

图3 Spark Streaming滑动窗口操作示意Fig.3 Spark Streaming sliding window operations

4 瓦斯浓度预测实验及分析

实验数据来自河南某煤矿3102综采工作面的煤矿安全监测系统。截取3102工作面回风隅角瓦斯传感器(编号001A08)的瓦斯浓度实测数据进行流回归预测和分析。001A08传感器以按采样速率0.2个/s收集瓦斯浓度数据，其中连续采样4 h的瓦斯浓度实测值序列如图4所示。实测值数据最大值为0.69%，最小值为0.02%，标准差为0.076。实时瓦斯浓度数据与前3次采集的浓度数据之间的Pearson相关性系数分别为0.948，0.901，0.871，具有较强的线性相关关系。此外，选取与该测点的Pearson相关性系数分别为-0.446，0.411，-0.397，-0.319的4个传感器监测点历史数据构建回归模型。

图4 瓦斯浓度实测数据Fig.4 The measured data of gas concentration

为模拟煤矿瓦斯传感器监测数据流，将瓦斯浓度序列数据通过TCP socket套接字以采样速率发送到Spark Streaming以模拟瓦斯浓度数据流，Spark Streaming则以内置数据流源socketTextStream接收瓦斯浓度流数据作为输入源。在进行瓦斯浓度流回归预测时，可根据实际应用的要求来指定Spark Streaming流窗口的长度和滑动距离，以确定流回归模型的训练数据长度和更新周期。为验证流回归的实时性和准确率，可通过设定相同时间窗口长度的训练数据，不同滑动距离来进行瓦斯浓度预测。实验采用流回归窗口长度为1 min，模型更新周期即滑动距离分别为60，45，30与15 s来进行瓦斯浓度实时预测。实验分4次进行，用以仿真不同模型更新周期下的瓦斯浓度数据预测准确率。图5显示了不同模型更新周期下的瓦斯浓度预测值与实际值的对比。从图5可以看出，不同模型更新周期的预测值与实际值都有较好的拟合性。

图5 不同更新周期的瓦斯浓度预测值与实际值Fig.5 The predicted data and measured data of gas concentration fordifferent update cycle of model

为了达到最优预测效果，实验采用均方根误差RMSE(root mean square error)来统计模型的精密度。RMSE为误差平方和均值的平方根，即：

当模型的时间滑动距离为60 s时，回归模型每隔60 s更新1次，根据模型的更新周期可知，流回归模型在4 h内更新了240次，分别计算每次流回归预测模型的RMSE。以此类推，当流回归预测系统的窗口滑动距离为40，30，15 s时，回归模型分别更新了320，480和960次。不同更新周期下流回归预测的RMSE变化如图6所示。

图6 不同更新周期的RMSEFig.6 RMSE of different update cycle of model

试验分析与统计的结果如表1所示，随模型更新周期的缩小，平均RMSE也依次减小。模型更新周期为60 s的模型平均RMSE最大，，而更新周期为15 s的平均RMSE为最小。而统计整体4 h的总体RMSE则15 s为最大，45 s为最小。从结果分析，模型更新过快，使数据集训练不充分，导致总体预测精度下降。而模型更新周期过长，则不能满足实时流数据处理要求。综合两者考虑，采用模型更新周期为45 s的流回归预测系统来预测瓦斯实时浓度。既使模型更新率满足实时数据流处理的要求，也可使流回归预测精度达到最优。

表1 不同更新周期预测效果对比分析

5 结论

1)利用基于内存的分布式流处理框架Spark Streaming构建基于流回归的瓦斯浓度实时预测系统，预测模型以瓦斯浓度实时数据流为训练集，在流式大数据中快速迭代建模与更新，在保证预测精确度的要求下，对瓦斯浓度数据进行实时预测。

2)应用Spark Streaming流回归预测系统来进行瓦斯浓度实时预测，可以使模型的更新周期达到秒级，同时，随着模型更新频率的加快，模型的平均预测精度也随之提高，而总体预测精度则根据煤矿瓦斯浓度采样率和测量误差来确定。

3)由于实验采取的瓦斯浓度数据是原始数据，并没经过噪声处理，且煤矿开采过程中影响瓦斯涌出的因素还包括开采强度，煤层厚度等诸多因素，但目前预测模型的建立仅仅考虑与预测点相关系数较高的传感器监控点所能实时测量的数据。因此，如何在流数据中既能进行浓度数据预处理，又能结合更多导致瓦斯涌出的因素来建立和动态更新模型以进一步提高瓦斯灾害预警精度是下一步研究工作内容。

[1] 张剑英, 程健, 侯玉华, 等. 煤矿瓦斯浓度预测的ANFIS方法研究[J]. 中国矿业大学学报, 2007, 36(4):494-498.

ZHANG Jianying, CHENG Jian, HOU Yuhua，et al． Forecasting coalmine gas concentration based on adaptive neuro-fuzzy inference system[J]. Journal of China University of Mining& Technology, 2007, 36(4):494-498.

[2] 杨丽, 刘晖, 毛善君, 等. 基于多元分布滞后模型的瓦斯浓度动态预测[J]. 中国矿业大学学报, 2016, 45(3):455-461.

YANG Li, Liu Hui, MAO Shanjun, et al. Dynamic prediction of gas concentration based on multivariate distribution lag model[J]. Journal of China University of Mining & technology, 2016, 45(3):455-461.

[3] 董丁稳. 基于安全监控系统实测数据的瓦斯浓度预测预警研究[D]. 西安: 西安科技大学, 2012.

[4] 张宝燕, 李茹, 穆文瑜. 基于混沌时间序列的瓦斯浓度预测研究[J]. 计算机工程与应用, 2011, 47(10):244-248.

ZHANG Baoyan, LI Ru, MU Wenyu. Study on gas concentration prediction based on chaotic time series[J]. Computer Engineering and Applications, 2011,47(10):244-248.

[5] 刘俊娥, 杨晓帆, 郭章林. 基于FIG-SVM的煤矿瓦斯浓度预测[J]. 中国安全科学学报, 2013, 23(2):80-84.

LIU June, YANG Xiaofan, GUO Zhanglin. Prediction of coal mine gas concentration based on FIG-SVM[J]. China Safety Science Journal, 2013, 23(2):80-84.

[6] 付华, 丰盛成, 刘晶, 等. 基于DE-EDA-SVM的瓦斯浓度预测建模仿真研究[J]. 传感技术学报, 2016, 29(2):285-289.

FU Hua, FENG Shengcheng, LIU Jing, et al. The modeling and simulation of gas concentration prediction based on De-Eda-Svm[J]. Chinese Journal of Sensors and Actuators, 2016, 29(2):285-289.

[7] 郭瑞, 徐广璐. 基于信息融合与GA-SVM的煤矿瓦斯浓度多传感器预测模型研究[J]. 中国安全科学学报, 2013, 23(9):33-38.

GUO Rui, XU Guanglu. Research on coal mine gas concentration multi-sensor prediction model based on information fusion and GA-SVM[J]. China Safety Science Journal, 2013, 23(9):33-38.

[8] 穆文瑜, 李茹. 基于K-Means聚类的瓦斯浓度预测[J]. 计算机应用, 2011, 31(3):702-705.

MU Wenyu, LI Ru. Prediction of gas concentration based on K-Means clustering[J]. Journal of Computer Applications, 2011, 31(3):702-705.

[9] 彭程, 潘玉民. 粒子群优化的RBF瓦斯涌出量预测[J]. 中国安全生产科学技术, 2011, 7(11):77-81.

PENG Cheng, PAN Yumin. Particleswarm optimization RBF for gas emission prediction[J]. Journal of Safety Science and Technology, 2011, 7(11):77-81.

[10] 曹博, 白刚, 李辉. 基于PCA-GA-BP神经网络的瓦斯含量预测分析[J]. 中国安全生产科学技术, 2015, 11(5):84-90.

CAO Bo, BAI Gang, LI Hui. Prediction of gas content based on PCA-GA-BP neural network[J]. Journal of Safety Science and Technology, 2015, 11(5):84-90.

[11] 刘奕君, 赵强, 郝文利. 基于遗传算法优化BP神经网络的瓦斯浓度预测研究[J]. 矿业安全与环保, 2015, 42(2):56-60.

LIU Yijun, ZHAO Qiang, HAO Wenli. Study of gas concentration prediction based on genetic algorithm and optimizing BP neural network[J]. Mining Safety & Environmental Protection, 2015,42(2):56-60.

[12] 唐亮, 李春生, 许虎, 等. 基于BP和RBFNN的神经网络算法在瓦斯预测中的应用及比较[J]. 中国安全生产科学技术, 2007, 3(6):31-34.

TANG Liang, LI Chunsheng, XU Hu, et al. The application and comparison of neural network based on algorithm BP and RBFNN in methane prediction[J]. Journal of Safety Science and Technology, 2007, 3(6):31-34.

[13] 胡俊, 胡贤德, 程家兴. 基于Spark的大数据混合计算模型[J]. 计算机系统应用, 2015, 24(4):214-218.

HU Jun, HU Xiande, CHEN Jiaxing. Big data hybrid computing mode based on spark[J]. Computer Systems and Applications, 2015, 24(4):214-218.

[14] Matei Zaharia, Tathagata Das, Haoyuan Li, et al.Discretized streams: fault-tolerant streaming computation at scale[A]. Proceedings of the Twenty-Fourth ACM Symposium on Operating Systems Principles[C]. Farmington, PA, November 03-06, 2013.

[15] Bar N, Ule G. Streaming Linear Regression on Spark MLlib and MOA[A]. Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining Paris France[C]. August 25-28, 2015.