黄土湿陷过程下埋地油气管道力学行为有限元模拟*
张 鹏,龙会成,李志翔,秦国晋,孙 灵
(西南石油大学 土木工程与建筑学院,四川 成都 610500)
0 引言
我国西部地区有较为丰富的油气资源。管道运输是我国将西部油气资源输送到东南部地区的主要途径。近几年国家持续推进西气东输、北气南下、西油东送和北油南调等工程,同时与俄罗斯、中亚和东南亚的国家建立能源进口通道,因此保障管道的安全运行将为我国经济发展提供有力支撑。
目前,输送我国西部地区油气资源的管道工程有西气东输管道、兰成渝成品油管道、兰郑长成品油管道和兰成原油管道等,从管线走向来看,均不可避免地要穿越广泛分布于我国西北部的黄土地区,西气东输管道穿过黄土高原,途经黄土梁峁沟壑区、黄土冲沟区、千阳-凤翔段黄土台塬、潼关段黄土台塬和豫西丘陵区冲沟区等黄土地形发育。黄土是第四纪形成的陆相黄色粉沙质土状堆积物,它以粉土颗粒为主,富含碳酸盐类,具有多孔性和柱状节理发育。湿陷性黄土在干燥或天然低湿度下往往具有较高的强度和较低的压缩性,但遇水后土体结构会迅速崩解破坏,土体强度迅速降低,产生大幅度的沉降,导致严重湿陷[1]。
油气管道穿越湿陷性黄土区时,若管沟填土未夯实,在遇到强降雨或农田灌溉时,原始结构被破坏的填土区容易发生湿陷并形成陷穴。据调查,仅兰郑长管道甘肃段就有黄土湿陷灾害35处之多。黄土湿陷灾害由产生到威胁管道安全的过程一般为[2]:
1)未被夯实且结构遭到破坏的管沟填土,在雨水和湿土自重作用下会发生沉降,产生局部负地形,为水流进一步汇入创造了条件。
2)水流汇入后,水头压力增大,带走黄土中的黏土粒和粉土粒,扩大土体节理、裂缝和动植物孔穴,溶解溶盐,产生陷穴。
3)水流找到出口后流速增大,溶蚀和土粒搬运能力增强,陷穴不断扩大,最终导致露管、管道悬空、管道下沉弯曲变形,由此造成管道破坏。
管道上部覆土湿陷下沉会导致管道浅埋,陷穴则会引起管道悬空,如图1所示。而陷穴属于隐蔽性灾害,不易察觉,有的陷穴规模较大,因此黄土湿陷灾害将极大影响管线的安全运行[3]。

图1 管道黄土湿陷灾害示意Fig.1 Sketch of buried pipe subjected to loess collapse
目前国内外学者针对管道下部土壤塌陷或沉陷对管道影响的研究[4-13]较多,包括试验研究和有限元分析,以及简化的力学建模[13]。同时,也有学者研究了各种地质灾害造成管道悬空时的力学行为及延寿对策[14-17],但对黄土湿陷过程性机理对埋地管道的影响鲜有研究报道。为此,采用有限元方法来模拟黄土湿陷形成陷穴造成管道悬空的过程,并将计算结果与解析值和实测值对比,分析湿陷过程不同阶段和湿陷区范围对管道的影响,为保障管线在黄土湿陷区安全运行提供理论指导。
1 黄土湿陷区悬空管道的力学模型
目前,埋地管道悬空的力学模型主要有Winkler弹性地基模型和理想弹塑性地基模型。前者没有考虑土的塑性变形,不符合黄土湿陷时土体变形的实际,而理想弹塑性地基模型更为精确。
1.1 悬空管道的理想弹塑性地基模型
图2为理想弹塑性地基的悬空管道力学模型,取黄土湿陷区管道悬空段中点建立的坐标系半模型。黄土湿陷产生陷穴导致的管道悬空段长度为2l1,受影响的管道长度为l2+l3,其中,l2为土体塑性变形区长度,该段管道受到的地基支撑力为kSc,k为土弹簧刚度系数,Sc为C处土体弹性变形和塑性变形的临界位移。长为l3的CD段土体为理想弹性,由Winkler弹性地基模型,该段土体对管道的支撑反力为kS(x)。

图2 理想弹塑性地基管道悬空力学模型Fig.2 Mechanical model of suspended pipe based on elastic-plastic foundation model
由图2可得到考虑轴力时管道任一截面弯矩:
AB段(0≤x≤l1):
(1)
BC段(l1 (2) CD段(l2 (3) 由梁的挠曲线微分方程-EIS″(x)=M(x),令: 可得各段微分方程: AB段: (4) BC段: (5) CD段: (6) 式中:M0为管道悬空段跨中截面弯矩;N0为管道在跨中受到的轴力;q为单位长度管道自重,为输送介质质量和管道上方覆土重量的总和。 解微分方程(4)~(6),并结合边界条件和连续性条件即可求得管道各截面弯矩和位移[16,19]。 黄土湿陷的陷穴导致管道悬空时,管道因弯曲变形、轴向载荷和内压作用产生的应力有[20]: 轴向应力:σa=σa1+σa2+σa3 径向应力:σr=-p 由von Mises屈服准则,可得管道的等效应力: 以ANSYS软件为平台,采用非线性面-面接触来建立管土相互作用三维有限元模型。管道由壳单元模拟,管材应力-应变关系采用三折线模型。黄土由实体单元模拟,本构关系为Drucker-Prager(D-P)模型。材料基本参数见表1。 表1 材料基本参数 按输送介质的不同,建立2种管道的有限元基本模型:输气管道外径1 016 mm,壁厚15.3 mm,管材为X80;输油管道外径610 mm,壁厚9.5 mm,管材为X65。管道埋深(土体表面到管道上表面距离)均为2.195 m。为避免边界条件造成的应力集中,学术界认为采用固定边界时管长应为管径60倍,其中非沉陷区管段长度为30倍管径[7]。因此,本文管土三维实体模型长度取为80 m,其中,非湿陷区70 m,湿陷区10 m,湿陷区网格加密。模型横截面根据尺寸取为正方形,考虑对称性,可建立1/4模型(如图3)。 图3 管土1/4有限元模型Fig.3 1/4 finite element model of pipe and soil 模型中对称面处管道和土体均施加对称约束,管道远端仅约束轴向位移。土体上表面自由,底面全约束,其他面除竖向位移外均约束。 考虑按设计压力输气和输油2种情况,其中输送介质密度按等效密度附加到管材密度上。设计压力10 MPa,按法向压力施加在壳体单元内表面。 黄土遇水湿陷时土体含水量增加,强度降低,产生沉降变形,因此参照边坡稳定性分析的方法,通过在13个时间步内等间距地逐渐改变湿陷区土体的密度、弹性模量、黏聚力和内摩擦角的途径来模拟土体湿陷[18]。首先在第1个时间步内计算埋地管道在基本黄土未发生湿陷时因自重产生的沉降,然后运用软件重启动技术,从第2个时间步开始按表2数据改变湿陷区土体参数,计算各时间步下地表土体不同湿陷量时下埋管道的内力和变形,以期实现在实际管道黄土湿陷灾害中通过测量地表沉降量这种便利的方式来把握暗埋管道的状态。 表2 湿陷区黄土各时间步参数 如前所述,埋设管道区域发生黄土湿陷灾害的根本原因,是管沟黄土与管沟区外原状黄土结构的不同。相关调查表明,长输管道湿陷性黄土区黄土陷穴长轴方向与管线走向基本一致,且离管道越近越明显[2],因此有限元基本模型中湿陷区宽度取为地表处管沟宽度。根据《油气长输管道工程施工及验收规范》(GB 50369-2014),初始输气管道模型中该宽度取为2.7 m,输油管道模型取2.5 m。 首先对有限元模型的可行性和计算结果的可信度进行验证。由于目前尚未发现相关试验或工程数据,因此采用文献[19]的理论解析值进行对比。同时,文献[16]中关于外径1 219 mm、壁厚17.2 mm的管道(其他参数与验证模型相差不多)在塌陷区长度50 m时的挠度数据,也具有参考价值,也可作为比较数据。 表3 湿陷区长度50 m时有限元计算结果验证分析 可见,以上有限元计算结果与理论解的相对误差较小,与实测值也非常接近,说明上文分析黄土湿陷过程下埋地管道的力学行为的有限元模型可行且可信,该方法比理论推导更为简便直观。 按2.3节黄土湿陷的模拟过程,最终土体湿陷沉降变形如图4和图5所示。图中可清晰地看出,湿陷区土体发生了明显的沉降变形,最大湿陷沉降量超过1 m,且在管道下部产生了沿管道轴向发展的陷穴。 图4 湿陷区局部剖面Fig.4 Part sectional view of the collapse area 对于输油管道,在模拟黄土湿陷过程中,土体达到最大湿陷量时管道的von Mises应力如图6所示。可以看出,该应力的最大值位于湿陷段中部上表面,数值大小为418 MPa,小于管材最低屈服强度450 MPa。同时还可发现,湿陷段下表面、湿陷段和非湿陷段交界处下表面都有较明显的应力集中。同样,输气管道应力分布情况也类似。 图5 湿陷区全图Fig.5 Total graph of the collapse area 图6 最大土体湿陷量下输油管道von Mises应力Fig.6 Von Mises stress map of pipe at the end of collapse 图7反映了土体达到最终湿陷沉降量时管道von Mises应力沿其轴向的分布(注意此处管道仅为半长),湿陷区管段为图中轴向位置在35~40 m的管段。由图7可知,无论输气还是输油,在土体发生湿陷时,湿陷区管段中部都有应力集中,且管道顶面的von Mises应力要明显大于底部。在管道轴向30 m左右位置,即土体湿陷区和非湿陷区交界处附近,因湿陷区管段产生竖向位移,使得湿陷区和非湿陷区土体刚度差异较大,管道底部也出现了应力集中。 图7 管道von Mises应力沿管道轴向的分布Fig.7 Distribution of pipe von Mises stress along its axial direction 图8反映了管道最大von Mises应力随土体湿陷沉降量的变化。显然,输气管道无论是在应力数值上还是应力随土体湿陷量的增速上均远小于输油管道。这是因为输气管道的管径和壁厚比输油管道要大得多,同时管材级别也高很多,而天然气的质量又远小于油品,导致土体湿陷下输气管道位移小于输油管道,这决定了应力曲线的变化特征。图中可见,输气管道模型中土体湿陷量小于0.3 m或输油管道小于0.5 m时,管道最大von Mises应力增加明显,之后趋于平缓。其原因是,湿陷前期土体湿陷对管道的位移影响显著,管道位移增长较快;后期因土体湿陷产生陷穴,管道悬空,位移增幅减小,应力增速减缓。 图8 管道最大von Mises应力随土体湿陷量的变化Fig.8 Relationship between maximum pipe von Mises stress and soil settlement 对管道应力曲线进行一元回归,可得优度拟合式: 输气管道: y=332.6x0.023(R2=0.986) (7) 输油管道: 本次调查共回收问卷201份,其中有效问卷175份,约有26名受访者表示根本不了解运费险。根据本文所要研究的问题和数据结果,在此主要从以下三方面进行分析。 y=416.5x0.087(R2=0.996) (8) 式中:y为管道最大von Mises应力, MPa;x为地表土体绝对湿陷量,m。可看出管道最大von Mises应力和土体湿陷量呈指数函数关系。 管道最大位移随土体湿陷量的变化见图9。由图可见,按2.3节模拟黄土湿陷过程时,输油管道在湿陷后期土体的湿陷量明显大于输气管道,原因是湿陷后期黄土早已软化,在管道和油品自重下会引起附加沉降,而管道按设计压力运行时,管道加油品的重量要远大于输气管道,在管土各方面因素的综合作用下湿陷量也就大得多。进一步观察还可看出,当输气管道中土体湿陷量小于0.3 m和输油管道小于0.5 m时,管道最大位移随土体湿陷量的变化明显,之后比较缓和。这是因为湿陷前期管道下部还未和土体脱离,2者一起运动。湿陷后期,因2者位移和刚度的不同,管道下方土壤脱离管道,产生陷穴,土体继续湿陷,而管道则保持悬空,同时管道上方荷载增加不大,因此管道最大位移增长较慢。 图9 管道最大位移随土体湿陷量的变化Fig.9 Relationship between maximum pipe displacement and soil settlement 对管道位移曲线作一元回归,得到优度拟合公式: 输气管道: |y|=0.026ln|x|+0.099(R2=0.984) (9) 输油管道: |y|=0.038ln|x|+0.144(R2=0.985) (10) 式中:|y|为管道最大位移绝对值,m;|x|为地表土体最大湿陷沉降量,m。可见,管道最大位移和土体湿陷沉降量呈近似对数函数关系。 在基本模型的基础上,逐渐增大湿陷区范围,分析此时对埋地管道的影响,计算结果见表4。 湿陷区长度为湿陷区沿管线方向的尺度,湿陷区宽度为湿陷区垂直于管线方向的尺度。大量计算表明,湿陷区长度对埋地管道的影响较大,而湿陷区宽度的影响不显著。根据计算数据,可以得到图10所示的管道最大应力随湿陷区长度的变化规律曲线和图11所示的管道最大应变随湿陷区长度的变化规律曲线。 表4 不同湿陷区范围下的计算结果 注:表中每列前1项针对输气管道,后1项针对输油管道。应力和应变是指von Mises应力和von Mises应变。 图10 管道最大应力随湿陷区长度的变化规律Fig.10 Change rule of maximum stress of pipe with length of collapse area 图11 管道最大应变随湿陷区长度的变化规律Fig.11 Change rule of maximum strain of pipe with length of collapse area 一元回归可得管道最大应力随湿陷区长度变化的优度拟合公式: 输气管道: σgas=13.53xl+198(R2=0.996) (11) 输油管道: (R2=0.995) (12) 式中:σgas,σoil分别为输气管道和输油管道的最大应力, MPa;xl为黄土湿陷区长度,m。可见,输气管道最大应力与湿陷区长度呈近似线性关系,而输油管道为非线性关系。 一元回归得管道最大应变曲线的优度拟合公式: 输气管道: εgas=7×105xl+0.001(R2=0.993) (13) 输油管道: (R2=0.998) (14) 式中:εgas,εoil分别为输气管道和输油管道的最大应力, MPa。可见,输气管道最大应变与湿陷区长度呈近似线性关系,而输油管道为非线性关系。 由图10和图11可知,随着湿陷区范围的增大,管道的最大应力和最大应变均逐渐增大,但因为管道参数和输送介质的不同,输气管道应力应变增幅比较均匀,且应力水平较低。而输油管道在屈服前应力增长较快,应变增长较慢,而在屈服产生塑性变形后应力增长很慢,应变则迅速增加。进一步观察输油管道应力、应变分布图后发现,随着湿陷区范围增大,应力和应变最值范围也逐渐扩大,由开始的湿陷区管段中部上表面向管道纵向和环向发展,最终湿陷区管段中部下表面,湿陷区与非湿陷区交界处附近管段上下表面也有最值分布。 1)从发生黄土湿陷灾害的原因及其机理出发,采用有限元方法实现了湿陷产生及陷穴形成过程的模拟,反映出该过程不同阶段土体最大湿陷沉降量对应的管道力学响应。 2)湿陷时土体沉降量、管道位移是管道和土体共同作用的结果。土体湿陷量随着水的不断侵入、土体结构的不断破坏而迅速增加,管道位移则是在陷穴产生前增长较快,此后减缓。管道最大von Mises应力也具有类似规律。 3)管道最大位移与土体湿陷沉降量呈近似对数函数关系,而管道最大von Mises应力与土体湿陷量呈近似指数函数关系。 4)由于土体湿陷,区域内管段会向下弯曲变形,湿陷范围较小时,会形成3个应力集中区:管段两端湿陷区和非湿陷区交界处的管道下表面、管段中部。而随着湿陷区范围的增大,管道最大应力和最大应变随之增大,并且在湿陷区管段中部和湿陷区与非湿陷区交界处管段的上下表面都有最值分布。 5)黄土遇水湿陷过程可以通过有限元分析来实现,文中考虑的是均匀湿陷沉降、陷穴贯穿湿陷区这种比较理想的情形,相关计算结果也与已有的实践经验相符。在该模型下考虑实际陷穴的分布,持续分析湿陷深度和管道参数等变量的影响,是需要进一步开展的研究工作。 [1] 杨德彪. 管道湿陷性黄土灾害风险评价技术研究[D]. 成都:西南石油大学,2014. [2] 付攀升,刘高,刘从友,等. 湿陷性黄土区某长输管道黄土陷穴灾害研究[J]. 西部探矿工程,2010,22(2): 21-24. FU Pansheng, LIU Gao, LIU Congyou, et al. The study on the loess sinkhole hazard along a long-distance pipeline in the collapsible loess area[J]. West-china Exploration Engineering, 2010,22(2): 21-24. [3] 蔡柏松,朱建华,杨晓宁. 黄土陷穴对陕京输气管道的危害及处理[J]. 油气储运,2002,21(4): 35-36. CAI Baisong, ZHU Jianhua, YANG Xiaoning. The methodology to protect the loess sinking in Shanxi-Beijing gas transmission pipeline[J]. Oil & Gas Storage and Transportation, 2002, 21(4): 35-36. [4] 杨朝娜,白晓红. 地基塌陷过程中埋地管线的有限元分析[J]. 科学技术与工程,2014,14(33): 266-271. YANG Zhaona, BAI Xiaohong. Numerical analysis for influence of foundation collapse on buried pipelines[J]. Science Technology and Engineering, 2014, 14(33): 266-271. [5] 吴际渊. 地基塌陷对城市地埋管线影响的试验研究及数值分析[D]. 太原:太原理工大学,2013. [6] 巨玉文,吴际渊,贺武斌,等. 地面塌陷对城市地埋管线影响的试验研究及数值分析[J]. 太原理工大学学报,2015,46(1): 64-68. JYU Yuwen, WU Jiyuan, HE Wubin, et al. Experimental study and numerical analysis on influence of urban underground pipelines under the ground collapse[J]. Journal of Taiyuan University of Technology, 2015, 46(1): 64-68. [7] 史永霞. 埋地管线在沉陷情况下的响应分析[D]. 大连:大连理工大学,2007. [8] Alawaji H A. Leak induced settlement of buried pipelines in collapsible soil[C]// International Pipelines Conference. 2008:1-10. [9] LIU C G, ZHANG S B. The response analysis for buried pipelines in nuclear power plant subjected to the subsidence[C]// China-Japan-Us Trilateral Symposium on Lifeline Earthquake Engineering. 2013:192-199. [10] WANG X, SHUAI J, YE Y, et al. Investigating the effects of mining subsidence on buried pipeline using finite element modeling[C]// International Pipeline Conference. 2008:601-606. [11] 柳春光,史永霞. 沉陷区域埋地管线数值模拟分析[J]. 地震工程与工程振动,2008,28(4): 178-183. LIU Chunguang, SHI Yongxia. Numerical analysis of buried pipelines subjected to the settlement[J]. Journal of Earthquake Engineering and Engineering Vibration, 2008, 28(4): 178-183. [12] 胡煜文. 场地震陷对地下管线影响研究[D]. 哈尔滨:中国地震局工程力学研究所,2008. [13] 韩腾飞,赵子皓. 土体塌陷下各参数对埋地管线的影响[J]. 科学技术与工程,2013,13(25): 7588-7590. HAN Tengfei, ZHAO Zihao. The impact of buried pipeline by change different parameter under the condition of soil collapsing[J]. Science Technology and Engineering, 2013, 13(25): 7588-7590. [14] 张鹏,魏韡,崔立伟,等. 地表冲沟条件下悬空管道的力学模型与延寿分析[J]. 天然气工业,2014,34(4): 142-148. ZHANG Peng, WEI Wei, CUI Liwei,et al. A mechanical model and life extension analysis of the suspended pipelines under the condition of geological gulch [J]. Natural Gas Industry, 2014, 34(4): 142-148. [15] 马廷霞,吴锦强,唐愚. 成品油管道的极限悬空长度研究[J]. 西南石油大学学报自然科学版,2012,34(4): 165-173. MA Tingxia, WU Jinqiang, TANG Yu. Maximum suspended length of production pipeline[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2012, 34(4): 165-173. [16] 王同涛,闫相祯,杨秀娟. 基于弹塑性地基模型的湿陷性黄土地段悬空管道受力分析[J]. 中国石油大学学报自然科学版,2010,34(4):113-118. WANG Tongtao, YAN Xiangzhen, YANG Xiujuan. Force analysis of suspended pipeline in collapsible loess areas based on elastic-plastic foundation model[J]. Journal of China University of Petroleum(Science & Technology Edition), 2010, 34(4): 113-118. [17] 魏孔瑞,姚安林,张照旭. 埋地油气管道悬空沉降变形失效评估方法研究[J]. 中国安全科学学报,2014,24(6): 68-73. WEI Kongrui, YAO Anlin, ZHANG Zhaoxu. Study on method for assessing failure of settlement and deformation of buried oil and gas suspended pipelines[J]. China Safety Science Journal, 2014, 24(6): 68-73. [18] 胡宇秋. 基于ANSYS降雨对黄土边坡稳定性影响的分析[J]. 中外建筑,2015(7): 179-182. HU Yuqiu. The influence of rainfall on loess slope stability based on ANSYS [J]. Chinese and Overseas Architecture, 2015(7): 179-182. [19] 尚尔京. 川气东送工程中地层塌陷及土壤液化区段管道安全评估 [D]. 青岛:中国石油大学(华东),2009. [20] 帅健,于桂杰. 管道及储罐强度设计 [M]. 北京:石油工业出版社,2006: 17-18,55.
1.2 管道应力计算和强度分析


2 黄土湿陷区管土相互作用有限元模型
2.1 基本参数

2.2 有限元模型
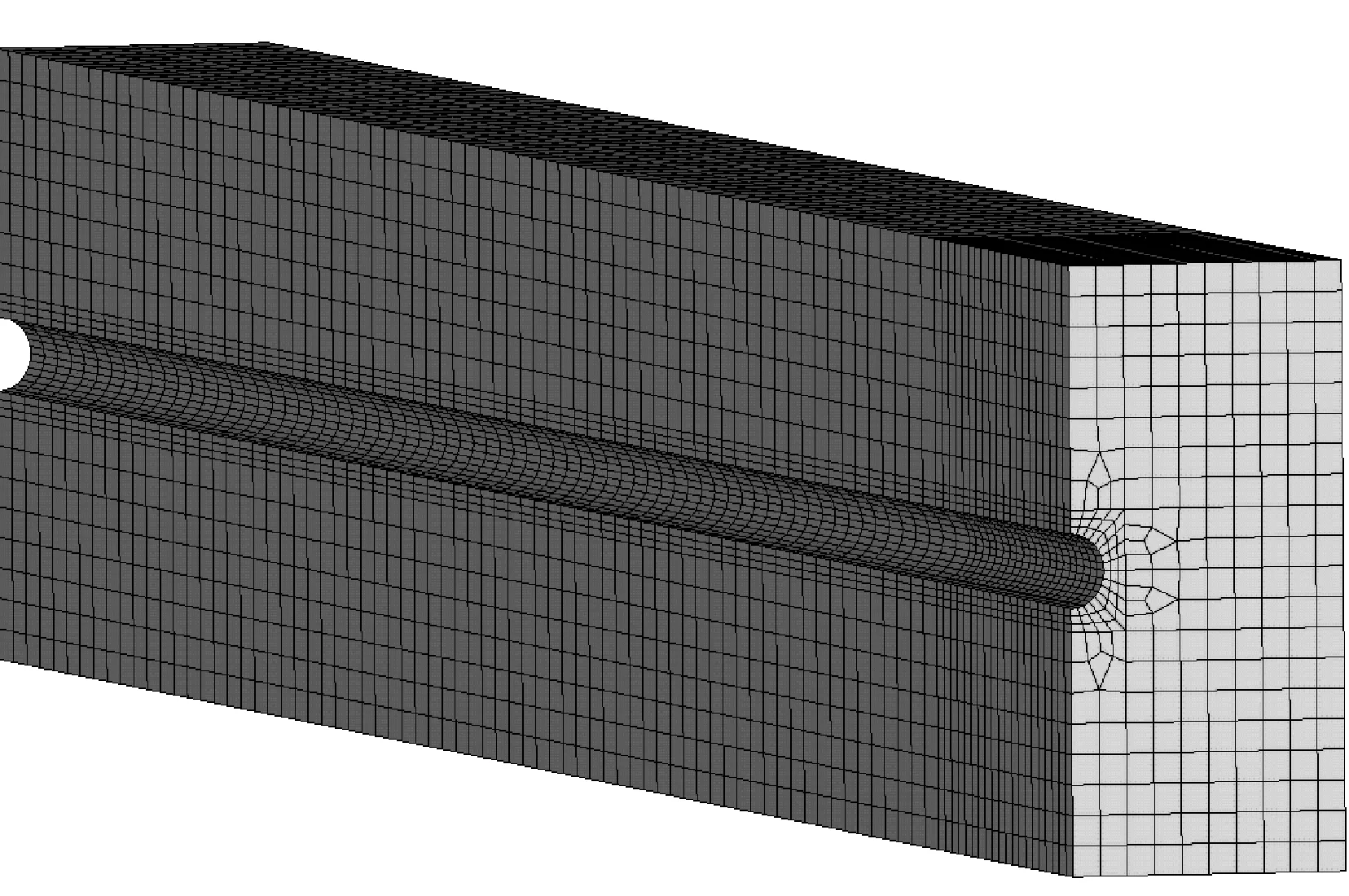
2.3 黄土湿陷过程模拟

3 有限元结果验证

4 湿陷效果及湿陷下管道的应力分析





5 土体湿陷下管道位移变化规律

6 湿陷区范围对埋地管道的影响



7 结论

