基于误差修正距离约束的深井巷道目标定位算法*

余修武，张 可，周利兴，张 枫，胡沐芳，刘 琴

(1.南华大学 环境保护与安全工程学院，湖南 衡阳 421001；2.中钢集团马鞍山矿山研究院有限公司 金属矿山安全与健康国家重点实验室，安徽 马鞍山 243000)

0 引言

实现井下人员、机车的实时定位，不仅有利于资源的合理调配，且对矿难发生时及时抢救，减少生命财产损失有着重要的意义[1]。特别是深井的自然环境十分恶劣，常伴随着高温高湿等不利于电缆布置的条件，加上环境因素导致线缆故障频发、维护不便，这种环境下无线传感器网络(WSN)技术的应用是目前较优的选择[2-4]。当前许多学者提出了多种人员定位算法，根据在定位过程中是否需要测量距离，可将定位方法分为：测距定位和非测距定位2类[5]。前者常见的方法包括基于接收信号强度(RSSI)的定位算法[6-7]，如：基于PDR和RSSI的室内定位算法[8]、狭长直隧道环境RSSI加权质心定位算法[9]、人体穿透损耗模型在井下测距模型狭长空间的组合定位[10]、改进型能量传递测距模型应用于矿井定位[11]；后者常见的方法包括近似三角形内点测试法(APIT)[12]和基于跳数DV-Hop算法。这些模型都为井下定位提供了新的参考。对于定位算法，一方面定位精度不够，如文献[13]提出的圆外切Bounding-box WSN定位方法,另一方面定位精度较高但计算量太大，如文献[14]和文献[15]利用智能算法优化定位精度，均难以满足井下的定位需求。针对此问题，通过改进距离约束定位算法，引入误差系数与修正系数对其进行修正，在控制计算量较小的情况下，提高定位精度，以满足深井定位环境。

1 基于RSSI的测距模型

RSSI测距的基本原理是利用信号强度与距离的关系，并以此建立数学模型。常用的模型有对数距离路径衰减模型、自由空间传播模型、对数—常态分布模型等，对于井下环境，通常考虑对数—常态分布模型。对数—常态分布模型的表达式如式(1)所示。

P(d)=P(d0)-10δlg(d/d0)+Xσ

(1)

式中：P(d)为收发节点距离为d时的接收信号强度；δ为路径衰减因子，其数值取决于无线信号的传播环境，是个经验值；d0为发射节点和参考节点之间的距离，一般取1 m；Xσ为标准差，是σ的零均值正态分布随机变量；P(d0)为参考点处的接收信号强度。

为了简化式(1)模型，通常忽略随机变量，即Xσ，如式(2)所示。

(2)

移动节点接收到定位节点的信号强度为PR，由式(2)可得移动节点与定位节点的距离，如式(3)所示。

(3)

2 距离约束定位方法

考虑1个移动节点和2个定位节点的情形，如图1所示，未知节点C收到A和B2个定位点发射的电磁波信号，设AC长度为d1，BC长度为d2，设定位节点A和B发射信号强度相同，移动节点接收到节点A的信号强度为PR1，移动节点接收到节点B的信号强度为PR2，根据式(3)可以得d1，d2的表达式，分别如式(4)和式(5)所示。

图1 1个未知节点和2个定位节点Fig.1 An unknown with two nodes

(4)

(5)

可得距离比公式，如式(6)所示。

(6)

在三角形ABC中有式(7)。

(7)

对于井下巷道狭长的空间结构，通常只有3～6 m宽，而长度有几十甚至几百米，在这种条件下，巷道的宽度对于部署的定位节点的距离可以忽略，也就是图1中，CD长度相对于AD与BD的长度可忽略，这样AC与BC的长度比值约为AD与BD的长度比值，即式(7)可简化得到式(8)所示。

(8)

图2 距离约束未知节点位置计算Fig.2 Calculation of distance constraint

如图2所示，将矿井巷道空间以EF为y轴，EG为x轴建立直角坐标系，K为EH，GF交点，EH与EF的夹角已知，设其为α，FG的长度设为L，其中各个点坐标分别为：E(0，0)，F(0，Lcosα)，H(Lsinα，Lcosα)，I，J分别为未知节点M到EH与GF的垂足,设I，J的坐标分别为：I(Ix，Iy)，J(Jx，Jy)，通过式(6)、式(8)可得到EI与IH之比，进而可求得点I的坐标，同理可求得点J的坐标。

设点M坐标为(Mx，My)，向量EI(Ix，Iy),MI(Ix-Mx，Iy-My)，GJ(Jx-sinα，Jy)，MJ(Jx-Mx)，已知EI和MI垂直，GJ与MJ垂直，因此有EI·MI=0,GJ·MJ=0，列出方程组得到式(9)。

(9)

将测距的信息代入式(9)，求解方程组即可得到未知节点M的位置坐标。

3 改进算法

3.1 误差分析

1)利用图1所示的AC与BC的长度比，来近似AD与BD的长度比，本身就存在1个近似误差，该误差会随着CD的长度不断增加而增加。并且随着CD的增加，近似垂点的位置会越偏向于中点位置，即偏离实际垂点越远，导致误差偏大。

2)若未知节点位于巷道定位节点周围，则它与定位节点的距离较近，类似于图1中CD相对于BC，AC长度无法被忽略，从而导致估计值存在较大偏差。

3)井下巷道的复杂空间与电磁环境使得电磁波容易受到各种干扰，如多径效应以及机电设备的噪声等，这些都会对定位的精度造成影响。

3.2 改进定位算法

在图1三角形ABC中，AC，BC，AB长度分别为d1，d2，d3。首先提出误差系数ω与修正系数ε，其中ω与ε的值分别如式(10)与式(11)所示。

(10)

ε=(1-ω)n·|d1-d2|

(11)

在巷道环境中，如图3，以EG为x轴，EF为y轴建立直角坐标系，同样设FG的长度为L，EH与EF夹角为α，其中E(0，0)，F(0，Lcosα)，H(Lsinα，Lcosα)，K(Lsinα/2，Lcosα/2)，I(Ix,Iy)，J(Jx，Jy)，I，J分别为未知节点M到EF与GF的垂足。对于三角形EMF，GMH，EMH，GMF，分别求出其对应的误差系数，设其值为ω1，ω2，ω3，ω4，选取其中误差系数最大的2个误差系数所对应的三角形，在这2个三角形中利用式(8)的近似公式得到初步估计的垂点位置，然后利用修正系数予以修正，再利用向量点乘等于0，求出未知节点的坐标。假设未知节点为图3中的M点，实现定位具体步骤如下：

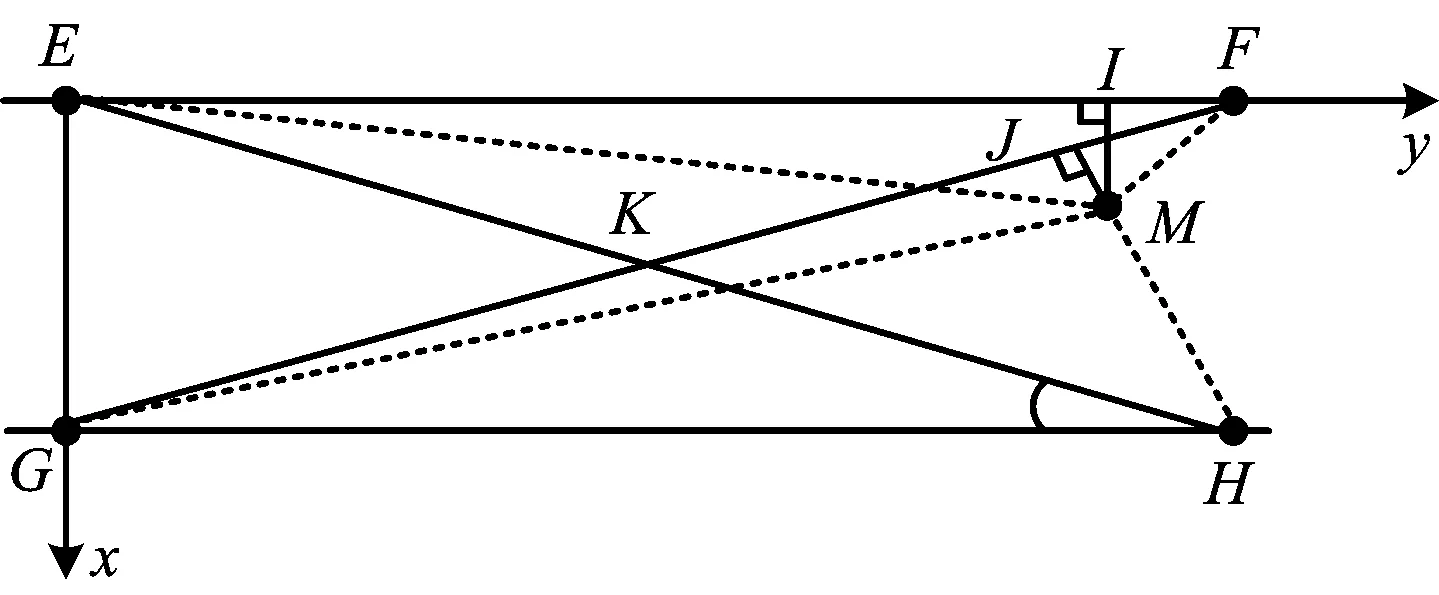
图3 改进距离约束定位示意Fig.3 Calculation of improved method

1)首先对三角形EMF，EMH，GMF，GMH分别算出其对应的误差系数ω1，ω2，ω3，ω4，并按照大小进行排序，对于图3情况，不妨假设误差系数大小排序为ω3>ω1>ω2>ω4。

2)选取其中最大的2个误差系数对应的三角形，为了避免出现两垂线相平行的情况，当最大的误差系数为ω1，ω3时，选取按误差系数大到小排序的第1和第3所对应的三角形，对于图3情况，则选取三角形GMF和EMF，在这2个三角形中，利用式(8)的原理进行近似，通过测量的RSSI的信号强度的比值，来得到初步估计的垂点I0，J0的位置，如图4所示。

图4 未知节点局部放大Fig. 4 Enlarged view of unknown point

3)通过误差修正系数对初步估计的垂点位置进行修正。如图4所示，设初步估计的垂点为I0(I0x，I0y)，J0(J0x,J0y)，由于有近似误差的影响，初步估计的垂点位置I0，J0会比实际垂点I，J偏向于EH，GF的中点方向，即EH，GF的交点方向。在三角形GMF中，由移动节点M接收到的点F与点G的信号强度与式(1)、式(8)可以得出MF与MG的距离比值，从而进一步得到MF与MG的距离DMF，DMG；在三角形EMF中同样可以得到ME的距离DME。ε1，ε2分别为三角形GMF，EMF的修正系数，Jx，Jy由J0x，J0y，μ1，μ2通过修正系数计算得到，计算如式(12)、式(13)所示。

Jx=J0x+μ1ε1|J0x-Lcosα|

(12)

Ix=I0x+μ2ε2|I0x-Lcosα|

(13)

(14)

(15)

4)将Ix，Jx代入其所在直线的方程中，得到Iy，Jy，再将I，J坐标数据代入式(9)解得未知节点M(Mx，My)。

对于式(11)中修正系数ε定义中的n值的确定，由于n的取值与巷道环境、节点布置的距离以及巷道的宽度相关，所以n值的确定通过仿真实验取不同值，比较平均误差选取合适的n值。

4 仿真与分析

在仿真实验中，仿真场景为50 m×6 m的狭长长方形区域，定位节点部署在长方形区域的4个顶点，在长度上将其分为25等份，并且在纵向的等分线上随机取5点，共取5×24=120点，如图5所示。通过仿真，比较基于距离约束的原定位算法与改进算法的误差，并进行分析。

图5 深井巷道节点布置Fig. 5 Nodes layout in deep mine roadway

设定巷道长度方向为Y轴方向，宽度方向为X轴方向。如图5所示，由于在深井的巷道中，宽度方向的坐标往往没有参考价值，因此仿真中的定位误差只考虑Y轴方向的定位误差。在等分线上随机取5点，以平均误差作为该长度位置的误差，当修正系数的n取值为1时，在理想情况下的仿真结果如图6所示。

图6 理想情况下的仿真结果Fig. 6 Result of Ideal condition

结果表明：基于距离约束的定位算法近似上存在一定误差，特别是靠近定位节点的位置的误差较大；改进算法的误差总体小于原算法，且近似误差趋于平稳，不存在靠近定位节点附近的误差较大情况，所以误差系数与修正系数能够有效的矫正由近似带来的误差。

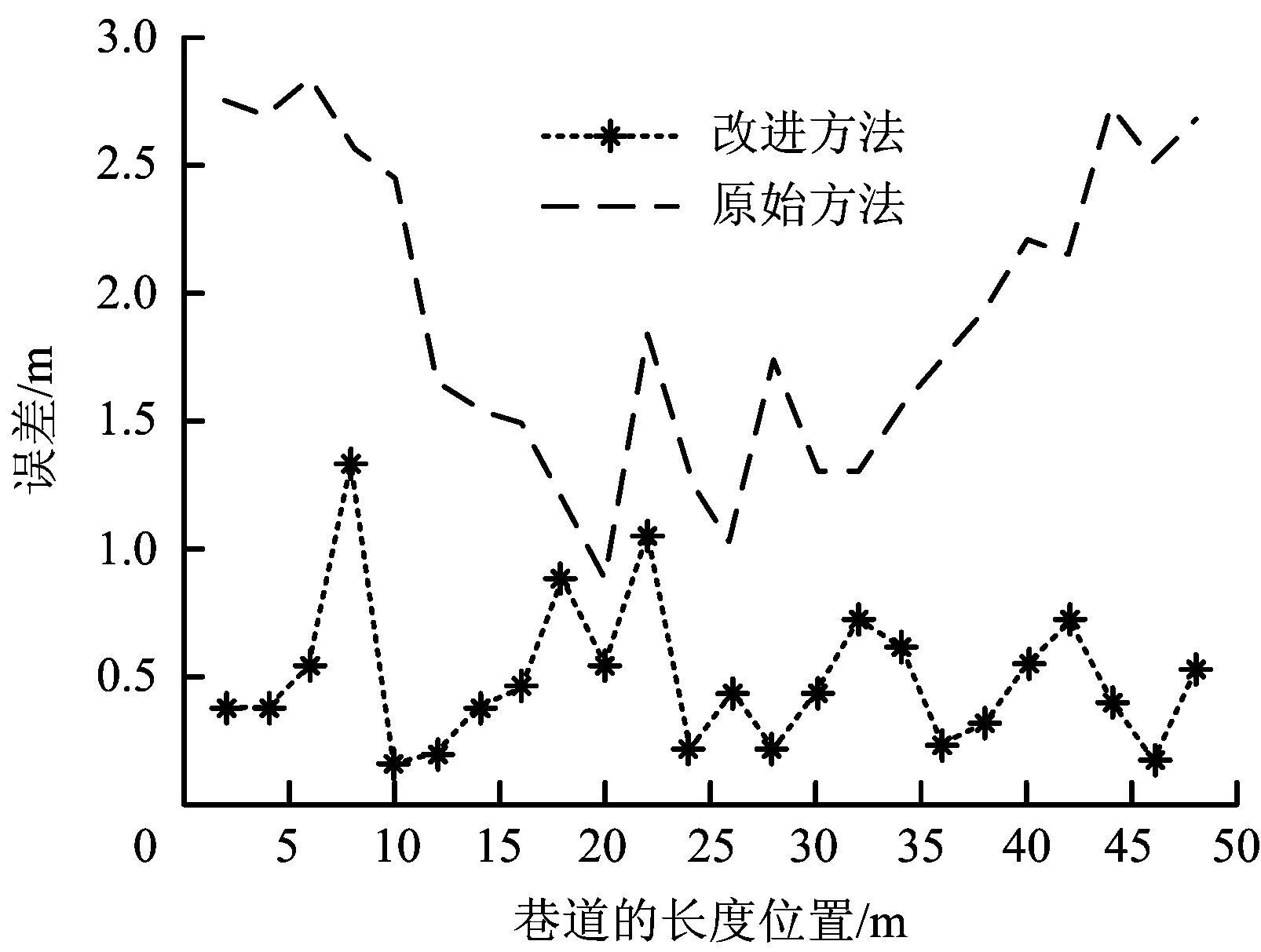
图7 加上定位噪声的仿真结果Fig.7 Result of Noise condition

当给RSSI测距定位加上均值为0、标准差为2的定位误差时，仿真结果如图7所示。结果表明：改进算法的平均定位误差远小于原定位算法，约为1/4，改进算法的最大误差小于1.5 m、最小误差为0.2 m，而原定位算法的最大误差接近3 m、最小误差也有1 m左右。

5 结论

1)针对基于距离约束的深井巷道定位算法本身存在的近似误差，尤其是在定位节点附近位置的近似误差较大的问题，提出了引入误差系数和修正系数的方法来改进定位算法，以误差系数为参考选取合理的近似三角形，同时利用修正系数来修正近似误差，提高了算法的定位精度。

2)理想仿真结果表明：改进定位算法有效地减少了靠近节点位置的近似误差；加入噪声条件下的仿真结果表明改进定位算法的平均定位误差远小于原定位算法，且误差变化更加平缓稳定，所以改进算法更加适用于对于定位精度要求更高的深井定位。

[1] 刘晓阳, 李宗伟, 方轲,等. 基于距离约束的井下目标定位方法[J]. 煤炭学报, 2014, 39(4):789-794.

LIU Xiaoyang, LI Zongwei,FANG Ke,et al.Underground target location method based on distance constraint[J].Journal of China Coal Society，2014，39(4):789-794.

[2] 余修武, 范飞生, 李睿,等. 基于接收信号强度分区矿山无线定位算法[J]. 中国安全生产科学技术, 2015,11(9):70-75.

YU Xiuwu, FAN Feisheng, LI Rui, et al.Study on wireless positioning algorithm in mine based on received signal strength paritition[J].Journal of Safety Science and Technology, 2015,11(9):70-75.

[3] 余修武, 周利兴, 范飞生,等. 基于新内点测试与Grid-SCAN的铀尾矿库监测定位算法[J]. 中国安全生产科学技术, 2016, 12(5):5-9.

YU Xiuwu，ZHOU Lixing，FAN Feisheng，et al.A localization algorithm for uranium tailings monitoring based on new interior point test and Grid-SCAN[J].Journal of Safety Science and Technology, 2016,12(5):5-9.

[4] 余修武, 张枫, 范飞生,等. 基于铀尾矿库核素污染监测WSN分簇路由协议[J]. 中国安全生产科学技术, 2016,12(10):154-159.

YU Xiuwu,ZHANG Feng,FAN Feisheng,et al.Study on clustering routing protocol of WSN for radionuclide contamination monitoring in uranium tailings[J].Journal of Safety Science and Technology,2016,12(10):154-159.

[5] 胡青松, 张申, 吴立新,等. 矿井动目标定位:挑战、现状与趋势[J]. 煤炭学报, 2016, 41(5):1059-1068.

HU Qingsong,ZHANG Shen,WU Lixin,et al.Localization techniques of mobile objects in coal mines:challenges,solutions and trends[J].Journal of China Coal Society,2016,41(5):1059-1068.

[6] 钱志鸿, 孙大洋, LEUNG Victor. 无线网络定位综述[J]. 计算机学报, 2016, 39(6):1237-1256.

QIAN Zhihong,SUN Dayang,LEUNG Victor.A survey on localization model in wireless sensor networks[J].Chinese Journal Of Computer,2016,39(6):1237-1256.

[7] 石欣, 冉启可, 范敏,等. 无线传感器网络动态加权DV-Distance算法[J]. 仪器仪表学报, 2013, 34(9):1975-1981.

SHI Xin,RAN QIke,FAN Min,et al.Dynamic weighted DV-Distance algorithm for wireless sensor networks[J].Chinese Journal of Scientific Instrument,2013,34(9):1975-1981.

[8] 郑学理, 付敬奇. 基于PDR和RSSI的室内定位算法研究[J]. 仪器仪表学报, 2015, 36(5):1177-1185.

ZHENG Xueli,FU Jingqi.Study on PDR and RSSI based indoor localization algorithm[J].Chinese Journal of Scientific Instrument,2015,36(5):1177-1185.

[9] 方旺盛, 高银. 狭长直隧道环境中WSN的RSSI加权质心定位算法[J]. 传感技术学报, 2014(2):247-251.

FANG Wangsheng,GAO Yin.A weighted centroid localization algorithm based on RSSI for wireless sensor network in straight narrow tunnel[J].Chinese Journal Of Sensors and Actuators,2014(2):247-251.

[10] 张晋升, 孙健, 李胜广,等. 狭长空间基于人体穿透损耗模型的组合定位方法[J]. 传感技术学报, 2016, 29(4):601-605.

ZHANG Jinsheng,SUN Jian,LI Shengguang,et al.Combination positioning method for long and narrow space based on the human body penetration loss model[J].Chinese Journal of Sensors and Actuators,2016,29(4):601-605.

[11] 孙继平, 王帅. 改进型能量传递测距模型在矿井定位中的应用[J]. 中国矿业大学学报, 2014, 43(1):94-98.

SUN Jiping, WANG Shuai.Application of the improved energy transfer ranging model mine localization[J].Journal of Safety Science and Technology, 2014,43(1):94-98.

[12] Liu J, Wang Z, Yao M, et al. VN-APIT: virtual nodes-based range-free APIT localization scheme for WSN[J]. Wireless Networks, 2016, 22(3):867-878.

[13] 罗清华, 焉晓贞, 彭宇,等. 圆外切Bounding-box WSN定位方法[J]. 哈尔滨工程大学学报(英文版), 2015(4):567-572.

LUO Qinghua,YAN Xiaozhen,PENG Yu,et al.A Bounding-box WSN localization method based on outer tangent line[J].Journal of Harbin Engineering University,2015(4):567-572.

[14] 宋慧敏, 杨社堂, 赵栋栋. 基于人工神经网络的无线传感器定位算法[J]. 计算机测量与控制, 2014, 22(2):473-475.

SONG Huimin,YANG Shetang,ZHAO Dongdong.ANN based localization algorithm for wireless sensor Network[J].Computer Measurement&Control,2014,22(2):473-475.

[15] 谭军. 人工鱼群算法优化支持向量机的无线传感器网络节点定位[J]. 计算机应用与软件, 2015(10):144-147.

TAN Jun.Wireless sensor network localization base on AFSA-SVM[J].Computer Applications and Software,2015(10):144-147.