Montgomery模乘法器的实现与优化
车文洁 董秀则 高献伟 张晓楠
(北京电子科技学院 北京 100070)
Montgomery模乘法器的实现与优化
车文洁 董秀则 高献伟 张晓楠
(北京电子科技学院 北京 100070)
蒙哥马利算法是公钥密码实现的基础算法, 应用范围广泛。要想提高公钥密码体制的运算速度,设计运算速度快、消耗资源少、效率高的蒙哥马利模乘法器非常关键。根据蒙哥马利乘积算法实现了蒙哥马利乘法器,通过硬件描述语言分别对其进行FPGA设计与实现,将其实现结构由串行结构优化为并行结构,在多占用资源约50%的基础上,速度实现了6倍左右的提高。与现有的相关研究成果相比,在增加耗用较少的资源的基础上速度实现大幅度的提升。
Montgomery算法 Montgomery模乘法器 FPGA 硬件描述语言协同
0 引 言
ECC是目前应用最广泛的一种公钥密码算法,它具有密钥量小、灵活性好及安全性高等优点。许多公钥密码的运算只能在素域上进行,所以素域上公钥密码的应用较广泛[1,2,7]。 模算术运算为素数域上的公钥密码算法基本运算。其操作数通常为大整数,运算复杂度高,成为制约公钥密码系统性能的瓶颈[8-9]。素域上模算术运算中的乘法运算是最基础、也是最耗时的运算,因此,要提高公钥密码体制的运算速度,设计运算速率高、资源消耗少的高效模乘法器很关键[10-11]。提到模乘法器,目前研究的热点是Montgomery算法,该算法是1985年由Peter L.Montgomery于提出[12]。 其实用性强,不仅适合软件实现,而且适合硬件实现。本文设计的蒙哥马利乘法器,其实现代码的通用性强,即通过修改相关的参数,可在384-bit内任意的素数域上实现。考虑到实用性与安全性,本文对操作数为384-bit的蒙哥马利乘法器在实现的基础上进行优化,其与现有的研究成果作比较,综合性能较优。
1 Montgomery算法介绍
蒙哥马利算法的主要思想是通过简单的移位操作来代替除法,将原始操作数通过运算用蒙哥马利域里面的数表示出来,提高了效率, 大大降低了计算复杂度。
定义Montgomery乘积:
MP(x,y)=xyR-1modm
(1)
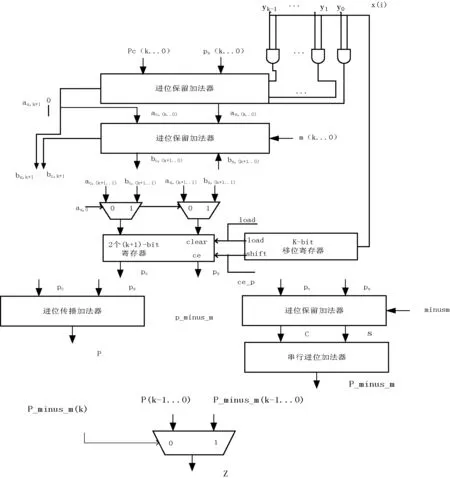
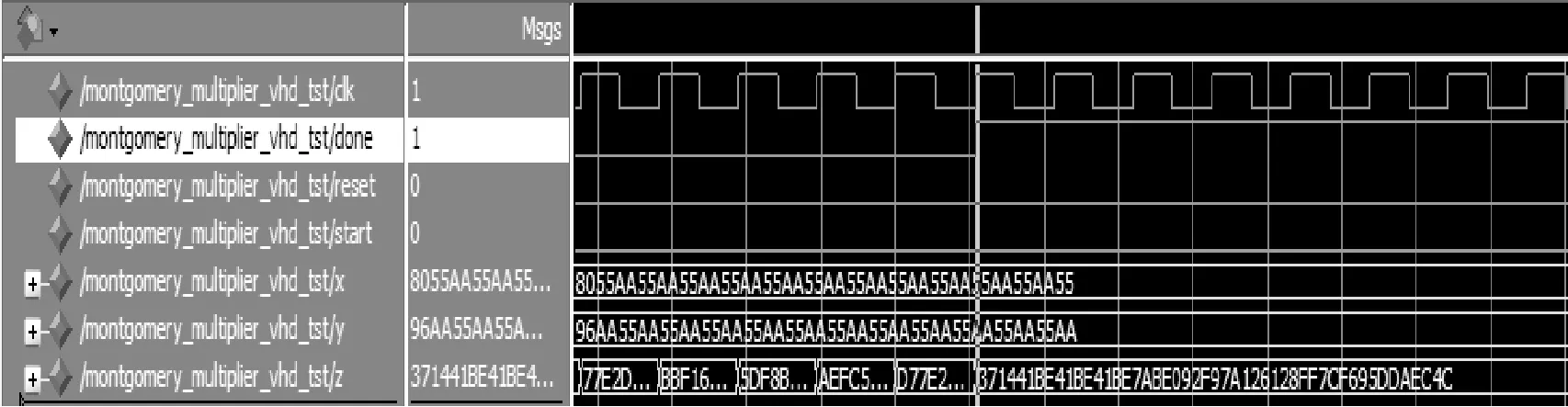
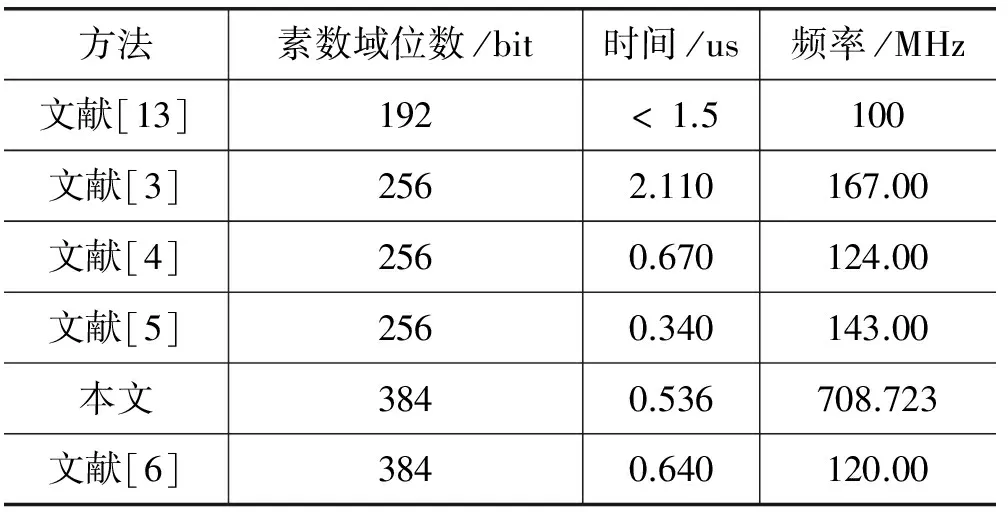
其中x、y 定义Montgomery约减: MR(x)=xR-1modm (2) 因为gcd(m,R)=1,所以存在-m-1∈ZR即m(-m-1)modR=-1。如果(-m-1)已被算出,用a来表示。Montgomery约减用下面的算法1来计算: 算法1Montgomery约减 a=(x mod R)(-m-1) mod R(0≤x≤R) b=(x+am)/R if b≥m then return (b-m) else return b; 从上面的算法求MR(x),可以看出,因为am≡xm(-m-1)≡-xmodR,故b为整数;因bR≡xmodmbR,则b≡xR-1modm。由于0≤x+am 给定x,y∈Zm,乘积p=xy MP(x,y)=MR(xy) (3) 若m是奇数,那么有元素2-1∈Zm,即2·2-1modm=1。若m的长度为k-bit,定义R=2k。给出x=xk-1·2k-1+xk-2·2k-2+…+x0·20,y∈Zm,则: MP(x,y) =xy(2k)-1modm =(xk-1y2k-1+xk-1y2k-1+…+ x0y20)(2k)-1modm =((…(((0+x0y)2-1+x1y)2-1+ x2y)2-1+…)2-1+xk-1y)2-1modm (4) 执行a·2-1如下: (5) 根据式(4)和式(5)推导出算法2: 算法2Montgomery乘积 p:= 0; for i in 0 .. k-1 loop qi:=( p0+ xi*y0)mod2; p:=(p+xi*y+qi*m)/2; end loop; if p >= m then z <= p-m; else z <= p; end if; 证明:p的值恒定小于2m的。如果p<2m,则a=p+x,y<2m+y<3m,a/2<(3/2)m<2m,(a+m)/2<4m/2=2m,这样,最后一步z就是p或p-m,均为小于m的数。 根据式(4)、式(5)以及算法2,借鉴串行进位加法器的实现结构,实现Montgomery乘法器,实现结构如图1所示。 图1 Montgomery乘法器的电路图 从该结构图可知,p是进位,y与xi相乘后与进位相加,对其和进行奇偶判断,若为奇数,则加m除以2,若为偶数,则直接除以2,将所得到的结果依次与后面的xi与y的乘积相加,直至x的最后一位,最后计算p_minus_m,若p_minus_m(k)为1,z为p_minus_m(k-1…0),否则z为p(k-1…0)。 该结构图的最小时钟周期约等于2kTFA,若不算最后的操作,则时钟总数为k,相应总的时间消耗为2k2TFA。最后操作包括计算p与p_minus_m,其中p为k-bit数,p_minus_m是(k+1)-bit数。使用串行进位加法器,计算时间大约是kTFA。因此,总的计算时间为: T≈2k2TFA+kTFA (6) 式(6)中的第二项kTFA对应于最后的操作,该操作不能在一个时钟周期内完成。 接下来我们来观察操作数为192-bit时,其操作仿真结果图。 取模数: m=p192=2192-264-1=(FFFFFFFFFFFFFFFFFF FFFFFFFFFFFFFEFFFFFFFFFFFFFFFF)16。资源消耗情况:共使用405个Registers,1 157个LUTs,仿真结果如图2所示。 图2 Montgomery模乘法器仿真结果(mod p192) 编译和仿真后得到Montgomery模乘法器的运行最高频率为199.898MHz,运行的总时钟数为304。根据公式:速度=最高频率(主频)/运行总时钟数,经过计算得出运行速度: 199.898MHz/304=657 559次/秒 图2中,x=(8055AA55AA55AA55AA55AA55AA55 AA55AA55AA55AA55AA55)16,y=(96AA55AA55AA55AA 55AA55AA55AA55AA55AA55AA55AA55AA)16时,z=(37 1441BE41BE41BE7ABE092F97A126128FF7CF695DDAEC4C)16。计算结果与仿真结果一致,验证了仿真结果的正确性。 接下来我们来观察操作数为384-bit时,其操作仿真结果图。取模数: m=p384=2384-2128-296+232-1=″fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffeffffffff000000000000 0000ffffffff″。资源消耗情况:共使用791个Registers,2 362个LUTs,仿真结果如图3所示。 图3 Montgomery模乘法器仿真结果(mod p384) 编译和仿真后得到Montgomery模乘法器的运行最高频率为131.673MHz,运行的总时钟数为602。根据公式:速度=最高频率(主频)/运行总时钟数,经过计算得出运行速度: 131.673MHz/602bit=218 725次/秒 图3中,X=′9807A0C5177CEF9817F58EA8BD4A8 D66503E9E22EAEA46EACF5BFCB0C6E683DDF80D5CF 2B3FB0D8B023E20CEE0475BD′,Y=′6EECFBD48A0 A4216F418049462C70894786708BB0D96F9B4C58240E 3AFF5E7E8F53DBCAAC99A62DF0BD6CF41BCE315F′, Z=′8AA51A52D7EE968848AED51E7941F9C22DC5F2F 5DEBDE5424A977C3A6F08EBBB863A1AE97FBC511328 6BC2E98F5DFAB2′,经过计算后得出结果与仿真结果一致,验证其仿真结果的正确性。 上小节虽然实现的Montgomery乘积,但整体实现结构为串行结构,总的计算时间约等于T≈2k2TFA+kTFA,时间消耗较多,速度也较慢。因此 使用进位保留加法器,将实现结构优化为并行结构,相应的实现结构如图4所示。 图4 优化后Montgomery模乘法器的电路图 在图4中,变量p根据存储-进位的形式表示,这样就能够使用进位保留加法器。 最后的操作包括计算p=pc+ps与p-m,其中pc和ps是(k+1)-bit数,m是k-bit数。假如不包括最后的操作,结构图4时钟周期的最小值约为2TFA,时钟总数为k,则总的计算时间近似为2kTFA。在计算pc和ps的结果后,最后的步骤分为两步:分别使用串行进位加法器计算pc与ps的和以及使用进位保留加法器、串行进位加法器计算pc、ps和minus_m的和,而进位保留加法器计算时间为TFA,相应的计算时间分别为kTFA和(k+1)TFA,则最后步骤的计算时间的最大值为(k+1)TFA,因此,总的时间消耗近似为: T≈2kTFA+(k+1)TFA (7) 式(7)中的第二项(k+1)TFA对应于最后的操作,该操作不能在一个时钟周期内完成。 资源消耗情况:共使用609个Registers,1 738个LUTs,仿真结果如图5所示。 图5 Montgomery模乘法器仿真结果(mod p192) 编译和仿真后得到Montgomery模乘法器的运行最高频率为725.018MHz,运行的总时钟数为213。根据公式:速度=最高频率(主频)/运行总时钟数,经过计算得出运行速度: 725.018MHz/213=3 403 755次/秒 图5中,x=(8055AA55AA55AA55AA55AA55AA55AA55AA55AA55AA55AA55)16,y=(96AA55AA55AA55AA55AA55AA55AA55AA55AA55AA55AA55AA)16时,z=(371441BE41BE41BE7ABE092F97A126128FF7CF695DDAEC4C)16。经验证,仿真结果正确。 接下来我们来观察操作数为384-bit时,其操作仿真结果图。 取模数: m=p384=2384-2128-296+232-1=″fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffeffffffff0000000000 000000ffffffff″。资源消耗情况:共使用1 208个Registers,3 467个LUTs,仿真结果如图6所示。 图6 Montgomery模乘法器仿真结果(mod p384) 编译和仿真后得到Montgomery模乘法器的运行最高频率为708.723MHz,运行的总时钟数为380。根据公式:速度=最高频率(主频)/运行总时钟数,经过计算得出运行速度: 708.723MHz/380=1 865 060次/秒 图6中,X=′9807A0C5177CEF9817F58EA8BD4A8 D66503E9E22EAEA46EACF5BFCB0C6E683DDF80D5CF 2B3FB0D8B023E20CEE0475BD′,Y=′6EECFBD48A0A 4216F418049462C70894786708BB0D96F9B4C58240E3 AFF5E7E8F53DBCAAC99A62DF0BD6CF41BCE315F′, Z=′8AA51A52D7EE968848AED51E7941F 9C22DC5F2 F5DEBDE5424A977C3A6F08EBBB863A1AE97FBC5113 286BC2E98F5DFAB2′,经过计算后得出结果与仿真结果一致,验证仿真结果的正确性。 优化前的结构图,使用的是串行进位加法器,操作数长度为k位串行进位加法器的总资源为一个全加器单元面积的k倍,每一个全加器单元计算时都要等待其低位全加器单元的进位输出。因此,总的时间消耗是一个全加器单元时间消耗的k倍,而整个实现结构是串行进行的,即每一步运算操作都要等待上一步运算操作完成后才能进行,因此实现速度较慢。 优化后的结构图,所使用的加法器为进位保留加法器,运算时,将进位保留,开始输入操作数并行运算,最后将运算的结果与进位的结果相加,只需两步则得出最后的结果。因为整个结构是并行进行的,最终结果的时间消耗等于两个FA(全加器)单元的时间消耗之和。因此大幅度地缩短了消耗时间,提升了速度。但因为需要寄存器保留进位,增加了其资源消耗。 现在,将优化前后Montgomery模乘法器做一个全面、系统的比较(本文所用的元器件为7vx980tffg1926-2),如表1所示。 表1 Montgomery模乘法器优化前后比较 通过优化前后Montgomery模乘法器的运算速度、资源占用情况的对比,我们可以看出:操作数为192-bit时,虽然优化后的Montgomery模乘法器较优化前相比,寄存器、查找表LUTs分别多出50.3%、50.2%,但是运算速度却比优化前的多出5.17倍。 操作数为384-bit时,优化后的Montgomery模乘法器较优化前相比,寄存器、查找表LUTs分别多出52.7%、46.7%,但是运算速度却比优化前的多出8.53倍。 此外,我们增加了一个比较量,即速度(万次/秒)/面积(LUT),通过比较速度/面积,分析算法的效率。可以看出优化后的Montgomery模乘算法比优化之前的Montgomery模乘算法效率平均高出4倍以上。如表2所示。 表2 性能对比分析 通过上述对比分析,可以看出优化后的Montgomery模乘法器与优化前的相比,在资源占用方面平均约高出50%,但是速度却平均高出6倍左右。当操作数较少(192-bit)时,速度高出5.17倍,但随着操作数增大,资源占用高出50%左右,而速度却高出8倍以上,优化效果明显。可以看出,通过多消耗少量的资源达到了明显提高速度的目的,这与设计原理一致。 将本文所设计优化的Montgomery乘法器与已有的Montgomery乘法器作比较,可以看出,本文优化后的蒙哥马利乘法器相比于文献[13]、文献[6]在时间、最高时钟频率上都有所优化。文献[13] 所用的元器件为2vp100ff1696-5,消耗LUTs的数目为5 188,最高时钟频率为100.0038MHz。文献[6]的工艺为FPGA,面积为2135LUT。本文优化后的蒙哥马利乘法器保持合理的可接受资源消耗的基础上,提高运算速度,较好发挥性能潜力。 本文应用VHDL语言,利用Montgomery模乘算法,设计出Montgomery模乘法器,并用ISE开发工具和Modelsim仿真软件对算法进行了仿真与测试,结果与理论一致,验证其正确性。其次,根据开始实现Montgomery模乘法器的结构图,将其串行运算的结构改进为并行运算结构,在多消耗少量资源的基础上,实现了速度的快速提升,成功实现了Montgomery模乘法器的优化。 [1] 高献伟,靳济方,方勇,等.GF(2m)域乘法器的快速设计及FPGA实现[J].计算机工程与应用,2004,40(25):111-112,123. [2] 葛亚明,彭永丰,薛冰,等.零基础学FPGA[M].机械工业出版社,2010:17-29. [3] 陈光化,朱景明,刘名,等.双有限域模乘和模逆算法及其硬件实现[J].电子与信息学报,2010,32(9):2095-2010. [4] 邬贵明,谢向辉,吴东,等.高基模Montgomery模乘阵列结构设计与实现[J].计算机工程与科学,2014,36(2):201-205. [5] 郭晓,蒋安平,宗宇.SM2高速双域Montgomery模乘的硬件设计[J].微电子学与计算机,2013,30(9):17-21. [6] 韩炼冰,黄锐,段俊红,等.基于FPGA的素域模乘快速实现方法[J].信息安全与通信保密,2013(9):76-78. [7] 周德金.32位高速浮点乘法器设计技术研究[D].江南大学,2008. [8] 周轶男,李曦,朱兆国.椭圆曲线密码算法的硬件设计与实现[J].计算机系统应用,2006(3):43-45,48. [9] 孔凡玉.公钥密码体制中的若干算法研究[D].山东大学,2006. [10] ÇetinKayaKoç,TolgaAcar.AnalyzingandComparingMontgomeryMultiplicationAlgorithms[J].IEEEMicro,1996,16(3):26-33. [11]RivcstR,ShamirA,AdlemanL.Amethodforobtainingdigitalsigna-turesandpublic-keycryptosystem[J].CommunicationsoftheACM,1978,21:120-126. [12]FranciscoR.NewAlgorithmsandArchitecturesforArithmeticinGF(2(m))SuitableforEllipticCurveCryptography[D].Corvallis,OR,USA:OregonStateUniversity,2000. [13] 梁鹏飞.基于流水线的Montgomery模乘算法硬件实现[D].华南理工大学,2011. IMPLEMENTATION AND OPTIMISATION OF MONTGOMERY MULTIPLIER Che Wenjie Dong Xiuze Gao Xianwei Zhang Xiaonan (BeijingElectronicScienceandTechnologyInstitute,Beijing100070,China) Montgomery algorithm is the basic algorithm of public key cryptography, which has a wide range of applications. Therefore, to improve the calculating speed of public-key cryptosystem, it is very important to design the Montgomery Multiplier with faster calculating speed, less resource consumption and high efficiency. This paper implements the Montgomery multiplier according to the Montgomery multiplication algorithm. It is designed and implemented respectively on FPGA by hardware description language and the implementation results are verified. Meanwhile, the implementation structure has been optimised(parallel one from serial one), which takes up 50% more resources but speed increases about 6 times. Compared with the existing relevant research results, the proposed multiplier achieves a substantial increase in speed on the basis of increasing consumption of fewer resources. Montgomery algorithm Montgomery multiplier FPGA Hardware description language 2015-12-30。车文洁,硕士生,主研领域:密码算法的硬件实现。董秀则,讲师。高献伟,教授。张晓楠,硕士生。 TP333.2 A 10.3969/j.issn.1000-386x.2017.03.0562 Montgomery乘法器的设计与实现



3 Montgomery乘法器的优化


4 结 语

