基于OpenCL的FFT算法研究

贾 格 彭先蓉 左颢睿

1(中国科学院光电技术研究所 四川 成都 610209)2(中国科学院大学 北京 100039)

基于OpenCL的FFT算法研究

贾 格1,2彭先蓉1左颢睿1

1(中国科学院光电技术研究所 四川 成都 610209)2(中国科学院大学 北京 100039)

快速福利叶变换在图像处理领域，尤其是在图像复原算法中作为常用的计算工具，将时域计算转变为频域计算，在工程应用中有着非常重要的意义。采取多线程分块以及并行的映射方法，可以使FFT算法最大程度并行。针对OpenCL的存储层次特点和算法层次的优化,在AMD GPU平台上取得了明显的加速效果。优化后的算法性能比具有相同处理能力的CPU平台提高了7倍，比具有相同处理能力的CUDA提高了4倍。

傅里叶变换 OpenCL GPU 并行加速

0 引 言

随着GPU通用计算的高速发展，大量的算法被成功移植到GPU平台，并且取得了良好的加速效果。而且GPU的应用研究也越来越广泛，通用计算适用领域也越来越大。但是已有的研究一般只限于单一的平台，而OpenCL(开放式计算语言)是面向异构计算平台的通用编程框架[2,3,6]，为GPU通用计算的跨平台移植提供了新的解决方案。由于GPU硬件结构体系本身的差异，造成了GPU硬件平台高效移植有很大难度，所以高效的移植不仅仅是功能的移植，高效的移植也就成为当前可待研究的问题。

1 OpenCL简介

OpenCL平台模型定义了使用OpenCL设备的一个高层描述[1]。这个模型如图1所示，OpenCL平台通常包含一个宿主机(host)和多个OpenCl设备。宿主机同OpenCl设备程序外部的交互，主要包括程序和I/O的交互。宿主机与一个或多个OpenCL设备连接，设备就是执行指令流(或kernel函数)的地方，通常OpenCL设备被称为计算设备。设备可以是GPU、CPU、DSP或者其他类型的处理器。图2所示为OpenCl的抽象模型。OpenCL应用执行模型中使用主机端程序对多个支持OpenCL的计算设备进行统一的调度和管理。图2中分别包括两个OpenCl设备，一个为CPU作为宿主机，一个GPU作为执行设备。然后定义了两个命令队列，一个是面向CPU的乱序命令队列，在宿主机上执行，另一个为面向GPU的有序命令队列，在OpenCl设备上执行。然后宿主机程序定义了一个程序对象，将这个程序对象分别编译后给两个OpenCL设备提供内核。接下来宿主机端定义程序所需的内核对象，并将他们分别映射到内核参数中。在OpenCL的内存模型中，通常根据线程访问权限的不同定义以下四种内存空间：分别为全局内存、局部内存、常量内存、和私有内存，它们在程序中的使用方式很大程度上决定了程序的性能，一般来讲，它们的大小和访问速度都是不同的。

图1 OpenCl平台模型

图2 OpenCl应用执行模型

2 FFT简介

快速傅里叶变换FFT是离散傅利叶变换DFT的快速算法[7,9]，具有广泛的应用研究和工程价值，常被应用于数字滤波和信号分解中。二维快速傅里叶变换(2D-FFT)是图像处理领域，尤其是在图像复原算法中作为常用的频域计算工具，在工程应用中有着非常重要的意义，典型的有图像频谱分析、卷积计算等。通常来说，在实际工程中会遇到高分辨率的图像，但是对于这种图像的二维傅里叶变换计算量非常大并且数据动态范围宽，硬件设计实现难度大，一定程度上制约了其在工程中的应用。通常的做法是利用二维傅里叶变换的数据可分性，图像的二维FFT可分为两次的一维FFT实现，分别是行方向和列方向。对于二维FFT的高速实现平台，一般以高性能DSP、FPGA、通用GPGPU芯片为核心器件的三种常用平台，并在系统设计中采用多核计算，多级流水线以及乒乓缓存等常用并行处理技术。本文利用二维傅里叶变换的共轭对称性，实信号变换周期对称性等特性减少存储资源和计算量，并通过OpenCL工具在GPU平台对算法加速。

3 FFT算法原理及其改进

3.1 利用周期对称性减少FFT算法冗余计算

对于实信号的FFT，通常利用傅里叶变换的对称性，可以将N点的实序列实现奇偶分离，变成一个N/2点的复数序列，将计算N点的实序列FFT变为一个N/2点的复数序列FFT，然后利用对应关系将N/2点的复数序列FFT输出对应到N点的实数序列结果输出。这样做将实信号FFT的计算量减少近一半。下面介绍它的基本原理：对于一个N点的实序列x(n)，我们根据奇偶序号，分别抽取奇数序列g(n)和偶数序列h(n)，分别将它们的离散傅里叶变换分别记为G(k)和H(k)。由FFT时间抽取基2算法得到如下关系式。

(1)

(2)

令y(n)=g(n)+j·h(n)，则y(n)为N/2点的复序列。y(n)的离散傅里叶变换Y(k)为：

(3)

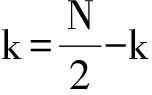
(4)

(5)

将复序列Y(k)、G(k)、H(k)的实虚部分开，分别记为Yr(k)、Gr(k)、Hr(k)和Yi(k)、Gi(k)、Hi(k)，代入式(5)，则有：

(6)

(7)

同理可以得到：

(8)

(9)

从上面两个式子可以看出，只需要得出构造的N/2点复序列y(n)的傅里叶变换结果Y(k)，然后利用上述四个关系式就可以得到g(n)和h(n)的结果G(k)和H(k)；然后再代入式(1)和式(2)，就可以得到N点实序列x(n)的傅里叶变换结果X(k)。实验中采取此种方法，可以将实信号FFT的计算量减少近一半，特别是针对于较高分别率的图像的时候，在N值取值比较大，节约的计算量对于运算速度的提升非常明显。

3.2 算法复杂度分析

如图3上半部分表示常规的2D-FFT运算，经过行变换后，再经过列变换，即输出结果；下半部分表示本文改进后的算法运算模块，多了数据预处理模块和数据恢复模块。其中，数据预处理：将输入分辨率为M×N的图像f(x,y)，对于各行数据按奇偶序号分离；然后将每行的奇、偶序列组成N/2点的复数数据fc(x,y)。数据恢复：对于N/2点的复数中间数据结果Fc(u,v)，根据式(6)-式(9)即可以得到F(u,v)的数据结果。

图3 常规算法和本文算法处理流程

本文改进方法大幅缩减了一维FFT的计算量，从N点变换转化为N/2点变换，计算量缩减了50%，但是引入的其他模块会带来一定的成本增量，导致计算成本要小于50%的减少量。表1在计算量，包括乘加次数给出了常规FFT算法和本文改进方法的比较。

表1 算法复杂度对比

表1中，M,N代表图像的尺寸大小,x,y代表额外等效的参数。在计算量方面，所有的计算等效为基本的乘加次数。对于无法转换的操作，比如数据的转存，移位开销则间接地等效成乘加运算。进一步可以得到本文方法相对常规方法所减少的计算量表达式：

(10)

(11)

从上式可知，减少量与图像的大小有关，图像越大，减少量相对更大。理论上分析，忽略数据转存以及内存中移位的时间开销，仅针对额外的数据计算，根据图3中数据预处理模块和数据恢复模块可知，x=2，y=4。对于128×128的图像，γ=39.286%,η=39.286%;对于512×512的图像，γ=41.7%,η=41.7%。从理论上分析，可以减少40%左右的计算量。

3.3 算法仿真分析

为了验证本文2D-FFT快速算法的正确性，以及计算效率。在个人PC平台上，使用Matlab软件环境，完成了4组对比试验，分别对64×64、128×128、256×256、512×512的图像进行了测试，测试结果如表2所示。

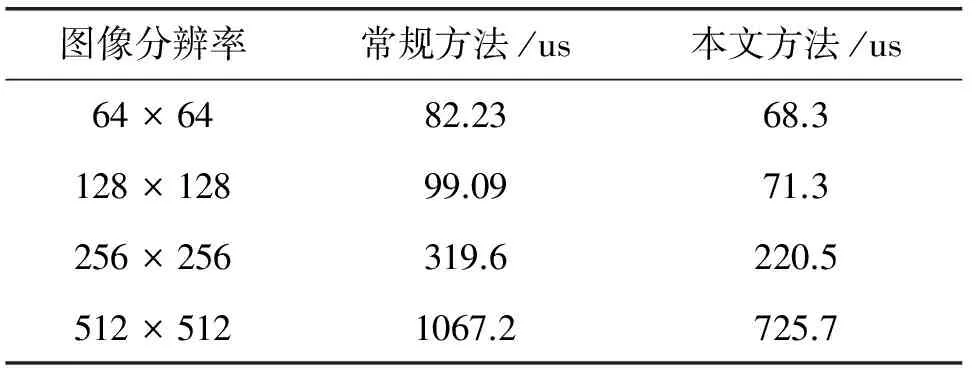
表2 二维FFT处理时间对比

可以看出，本文方法相对于常规方法速度有显著的提升，速度提升30%左右，接近于上面给出的理论提升量。实验表明改进算法具有快速处理的优点。图4为实验得到的频域数据图，(a)和(d)为常用的测试图Cameraman和Plane，(b)和(e)为本文算法得到的中间结果，(c)和(f)为恢复得到的最后结果。

图4 实验结果图

4 OpenCL实验结果及其分析

4.1 OpenCL算法实现

传统算法如图5所示[4]。一般的FFT采用三层循环，通常对于N点变换，可以分为M级，N=2M，每一级有N/2个蝶形单元。当前组完成后，完成下一组；当前级完成后，完成下一级；传统的方法都是串行的。如图5所示的8点的FFT变换，共分为3级，每一级间有4个蝶形运算，对于蝶形间的计算和级间的运算都是串行依次进行的。分析可知：在同一级中具有相同旋转因子的蝶形单元，可以通过备份多个旋转因子以达到并行执行；在同一级中具有不同旋转因子的蝶形单元，因为数据不存在相关依赖性，本身就是可以并行执行的；而对于相邻级使用的旋转因子也并非完全不同，根据这个规律可以将旋转因子存储为二维查找表来实现，减少计算量。

图5 N=8时，蝶形运算图

本文旨在将传统的算法通过OpenCl在GPU平台上进行并行加速，因此需要找出算法中可以并行的部分，对于算法并行粒度的划分如图6所示。对于二维FFT，局部工作组通常是一行或者几行的大小，局部工作组之间是并行的；由若干个线程组成一个线程块，然后由若干个线程块组成一个局部工作组，本文中最小的处理单元是一个线程，而一个线程对应着一个蝶形计算单元，即一个线程处理两个点的数据。线程块之间是并行的，算法中每个蝶形单元也是并行的，对于每个数据点都是并行计算的，FFT算法实现了真正的数据并行。试验中将旋转因子放到全局内存表中，将待处理的数据通过全局内存读取到局部内存中。

图6 算法并行粒度和存储共享

在OpenCL模型中，要取得足够高的加速性能，需要非常多的线程才能够提高计算效能，隐藏计算的访存延时，本文根据OpenCL多线程执行模式的特点，对FFT算法的分析如图7所示。将算法按级划分成M级，N=2M，每一级有N/2个蝶形运算单元，因为每一级的蝶形单元数据没有相关性，可以完全并行执行；在每一级间是数据通信，实验中采取原址计算，即将前级蝶形运算的结果继续存放在原来位置，而次级运算的时候，按照索引的地址从新位置读取数据，将上一级产生的结果输出作为后一级的数据输入，实现数据在各级操作级中流动起来。实验中分为log2N级，每一级中有N/2个线程块，每一个线程块完成一个蝶形运算，当每一级的蝶形运算完成后通过栅拦函数同步，数据流入下一级。然后下一级进行同类运算，直至完成M级计算。另外，每一个蝶形单元的两个输入操作数的地址根据线程号和当前级数共同确定。同步栅拦barrier是为了确保线程间的同步，保证数据的准确性。采用OpenCl提供的库函barrier(CLK_LOCAL_MEM_FENCE)实现线程块内的线程同步，它保证线程块中的线程执行到barrier处才继续执行后面的语句。通过同步可以避免当一个线程块中的一些线程访问共享存储器的同一地址时可能发生的读写错误问题。

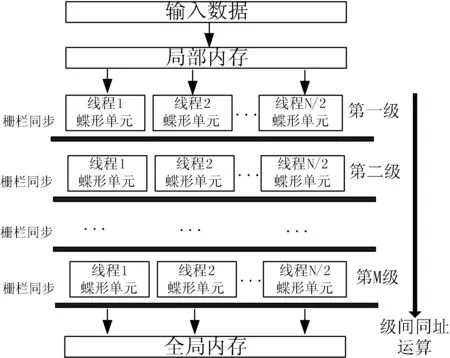
图7 算法多线程并行示意图

4.2 存储层次的优化

① 局部存储器是GPU片上的高速存储器，是能够被相同线程块中的线程同时访问的可读写存储器。在实验中，按照图7，将算法流程分为多级，上级的数据输出作为下一级的输入，数据完全在级间流动，数据操作采用同址方式。如果将输入数据从全局内存搬移到局部内存中，就可以大大提高线程访问数据的速度，通常来说全局内存具有非常高的访存延时。在内核函数设计中，首先将显存所需的数据搬迁到局部内存中，最后处理完成后，再从局部内存搬迁至显存中，计算过程，只在局部内存中完成，而访问全局内存也只需要两次，大大提高了计算效率。

② 进程的充分利用。在实验中针对N点FFT变换，实际上只用到了N/2个线程，将局部工作组划分为一行的时候，就会造成N/2个空线程的资源浪费。对于一个线程完成一个蝶形运算单元，也就是完成两点的数据变换，因此利用此点可以提高线程的利用率。实验中利用N个线程完成2N点的变换，每N/2个线程分别完成一行的变换，充分利用了线程，提高了计算资源的利用率，实验速度得到了显著提升。

③ 内存的读写优化。针对2D-FFT算法，有大量的存储数据读取，因此提高速度，可以对数据的读写进行优化。实验中读数据的读写速度进行测试，对于128×128的数据进行读取，从全局存储器读到共享存储器需要13μs，不论是按行读取还是按列读取；而从共享存储器写到全局存储器则需要分为按行写和按列写，按行写为32μs，按列写则是85μs，可以发现写的时候按行写会大大节省时间。在2D-FFT变换中，行变换完成后需要进行一个转置，接着进行列变换，对读写时间的分析得出最大耗时的地方是转置，所以实验中采取的做法是在行变换完成后仍然按行写到全局内存，在列变换的时候任然采取按列读，这样极大地减小了按列写的时间和转置的时间，实验速度得到了近40%的提升。

④ 内存的写优化。实验中发现在写的过程中，同样是按行写，但是按行顺序写和按行乱序写，仍然存在着速度的差异，因此在写的过程中，预先对数据排序后，然后依次往全局内存写数据，实验结果有一定的提升。

4.3 实验结果

本文在基于Windows操作系统上和AMDGPU实现了该算法，验证了OpenCL的FFT算法实际的性能。实验中所用到的平台和配置如表3所示，程序基于AMD的OpenCl开发包，并在OpenCl1.2的环境下编译。为了验证对比本文算法的性能，和文献[4]基于CUDA版本的算法以及基于CPU版本的FFT算法做了对比，其中文献[4]的处理器和显卡配置如表4所示。

表3 本文的平台配置

表4 文献[4]的实验硬件配置

现有的GPGPU通用计算的处理流程一般为：CPU端作为宿主机先处理少部分逻辑运算，然后通过调用API函数将大量的计算任务交给OpenCL设备(GPU)。但是内存和显存的实际位置不一样，所以CPU端通过内存对象将操作数据送到GPU显存中，等到GPU处理完毕，然后再通过内存对象送回到CPU内存中。实验中的计算时间为FFT算法的总运算时间，包括在CPU上执行逻辑函数的时间和在GPU上执行kernel函数的时间，以及从CPU拷贝数据到GPU显存的时间。表5对比了本文和其他平台的实验结果。

表5 FFT算法的运行总时间 单位：us

实验数据表明：当图像数据小的时候，GPU和CPU之间数据相互拷贝的时间会抵消很大一部分并行加速的时间，所以加速比很小，当数据规模增大的时候，这种加速效果就逐步提升。本文中AMD Radeon HD 7450支持最大工作组大小为256，所以只针对最大图像数据为512×512。从实验数据可以看出，文献[4]基于CUDA的方法和本文方法结果基本一致，相比较CPU版本有4～7倍的加速。但是考虑到NVIDIA GTX 465浮点运算峰值为1 277.7 GFLOPs，Inter i7 core 3770浮点运算峰值为282 GFLOPs，而AMD Radeon HD 7450的浮点运算峰值仅为300 GFLOPs，因此本文的算法相对于文献[4]有4倍的加速，相对于CPU版本有真正意义上的4～7倍的加速。对于同样浮点运算能力的处理器来说，这个加速效果还是很明显的。

5 结 语

本文实现了基于OpenCL的高速FFT计算。通过分析2D-FFT算法的可并行性特点，将算法分级，多线程分块，充分利用了数据间的非相关性，实现了数据的充分流动，极大地提高了并行度；针对OpenCL的存储层次特点和算法层次的优化，明显地提高了运算的速度，和相同浮点运算能力的平台相比，具有4倍左右的良好加速比。

[1] AMD上海研发中心.跨平台的多核与众核编程讲义OpenCL的方式[M].2010.

[2] Aaftab Munshi,benedict R Gaster,Timothy G Mattson,et al.OpenCL Programming Guide[M].Pearson Education,2012.

[3] AMD Corporation.Accelerated Parallel Processing OpenCL TM[Z].Jan.2011.

[4] 赵丽丽,张盛兵,张萌,等.基于CUDA的高速FFT计算[J].计算机应用研究,2011,28(4):1556-1559.

[5] 张樱,张云泉,龙国平,等.基于OpenCL的图像模糊化算法优化研究[J].计算机科学,2012,39(3):259-263.

[6] Khronos group.OpenCL-The open standard for parallel programming of heterogeneous systems[OL].http://www.khronos. org/opencl/.

[7] 温博,张启衡,张建林.高分辨图像二维FFT正反变换实时处理方法及硬件实现[J].计算机应用研究,2011,28(11):4376-4379.

[8] 左颢睿,张启衡,徐勇,等.基于GPU的并行优化技术[J].计算机应用研究,2009,26(11):4115-4118.

[9] 范进,金生震,孙才红.超高速FFT处理器的设计与实现[J].光学精密工程,2009,17(9):2241-2246.

RESEARCH ON FFT ALGORITHM BASED ON OPENCL

Jia Ge1,2Peng Xianrong1Zuo Haorui1

1(InstituteofOpticsandElectronics,ChineseAcademyofSciences,Chengdu610209,Sichuan,China)2(GraduateUniversityofChineseAcademyofSciences,Beijing100039,China)

Fast Fourier transform, as a commonly used computational tool in the field of image processing, especially in image restoration algorithm, transforms the time-domain computation into frequency-domain computation and has great significance for engineering applications. By adopting thread blocks and parallel mapping method, we can make FFT algorithm reach the maximum degree of parallelism. In view of the storage features of OpenCL and the optimisation of the algorithm, the AMD GPU platform has been significantly accelerated. Compared with CPU platform and CUDA with the same processing capability, the performance of the optimised algorithm has increased by 7 times and 4 times respectively.

Fast Fourier transform OpenCL GPU Parallel speedup

2016-01-20。贾格，博士生，主研领域：并行加速，图像盲复原。彭先蓉，研究员。左颢睿，副研究员。

TP302

A

10.3969/j.issn.1000-386x.2017.03.042