基于栈式自编码器模型的汇率时间序列预测

寇茜茜 何希平,2,3*

1(重庆工商大学电子商务与供应链系统重庆市重点实验室 重庆 400067)2(重庆市工商大学计算机科学与信息工程学院 重庆 400067)3(重庆工商大学重庆市检测控制集成系统工程实验室 重庆 400067)

基于栈式自编码器模型的汇率时间序列预测

寇茜茜1何希平1,2,3*

1(重庆工商大学电子商务与供应链系统重庆市重点实验室 重庆 400067)2(重庆市工商大学计算机科学与信息工程学院 重庆 400067)3(重庆工商大学重庆市检测控制集成系统工程实验室 重庆 400067)

针对目前具有非线性特征的金融时间序列浅层模型预测精度有限的问题，提出一种由底层的栈式自编码器和顶层的回归神经元组成的栈式自编码神经网络预测模型。首先利用自编码器的无监督学习机制对时间序列进行特征识别与学习，逐层贪婪学习神经网络各层，之后将栈式自编码器扩展为有监督机制的SAEP模型，将SAE学习到的参数用于初始化神经网络，最后利用有监督学习对权值进行微调。实验设计利用汇率时间序列作为训练及测试样本，与目前较成熟的方法进行对比实验，验证了所提出的模型在汇率时序预测应用中的有效性。

时间序列 预测 深度学习 栈式自编码器 特征学习 深度神经网络

0 引 言

基于时间序列分析的特征识别与预测已经成为国内外研究的热点，而构造有效的数据分析模型是精准预测的关键步骤[1]。对于现在普遍存在的时间序列来说，传统的浅层模型已经不能有效表达其深层次的特征[2]。为更好地模拟应用中的时间序列，目前通用的做法是设计特征选择器，但对于每项任务来说，设计特征选择器需要专家经验且耗时；另一种做法是从无类别标签的数据中采取无监督学习机制学习特征[3-4]，这一做法的优势在于无需设计特征选择器即可自动学习序列数据之间潜在的关联关系。深度神经网络产生于人工智能研究背景，并且已经在多个时间序列应用领域取得较好的结果，例如语音识别[5]、运动肢体识别[6]、视频目标分类[7]等。汇率时间序列具有动态性和不确定性，含有大量噪音干扰，通常呈现出非线性特征，对于汇率时序的预测一直是国内外金融研究中重要且具有挑战的工作之一[8]，目前对于汇率的时序预测模型有计量模型，例如ARIMA模型[9]、ARCH模型[10]、GARCH模型[11]，这些模型的改进及组合都在一定程度上推进了汇率预测的研究；另一类为基于机器学习的模型，例如人工神经网络(ANN)[11-13]和支持向量机(SVM)[14]。现有的模型预测精度受限问题主要集中在浅层学习难以挖掘时间序列的深层次特征。针对汇率预测精度受限的问题，本文提出一种由底层的栈式自编码器和顶层的回归层组成的深度学习预测模型，同时该模型的提出，尤其是无监督学习机制，为时间序列的实时性预测提供了一种新的思路和方向。

基于以上的分析，本文研究栈式自编码预测模型SAEP(Stacked AutoEncoder based Prediction model)及其汇率时序预测应用。首先，利用无监督逐层贪婪学习的自编码器，堆叠实现对深度神经网络的预训练，之后再用监督学习对网络参数进行微调，然后借助学习到的网络模型实现时间序列的预测。该模型尤其可以解决具有非线性特征的时间序列预测精度受限的问题。

1 栈式自编码器与预测模型

1.1 自编码器

自编码器AE(AutoEncoder)是尝试学习一个恒等函数，使得输出值等于输入值，现假设有一个时间序列样本{y(1),y(2),…,y(n)}，对于t时刻的自编码结构如图1所示。

图1 自编码器的结构

设W1∈Rk×m、b1∈Rk分别表示可视层V(VisibleLayer)与隐藏层H(HiddenLayer)的连接权值和偏置，W2∈Rm×k、b2∈Rm分别表示隐藏层与重构可视层的连接权值和偏置。假定每一个节点非线性激活函数为sigmoid函数，则对于自编码器的编码过程如式(1)所示。

(1)

解码过程为：

(2)

自编码器将输入y编码为新的表达h，再将h解码重构回y，通过反向传播算法来训练网络实现重构并恢复输入值。其关键在于求解参数{w,b}使得重构误差最小化。

若样本数为N，则自编码器输出误差代价函数可表示为：

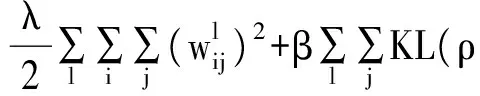
(3)

(4)

1.2SAE模型

通过堆叠n个自编码器构成了栈式自编码神经网络SAE(StackedAutoEncoder)，该模型中前一个自编码的隐层输出h(i-1)作为其后一层自编码可视层的输入V(i)，即：

V(i)=h(i-1)

其中i=2,3,…,n，即去除自编码器的解码层堆叠构成深度神经网络。n个自编码器堆叠而成的SAE结构如图2所示。

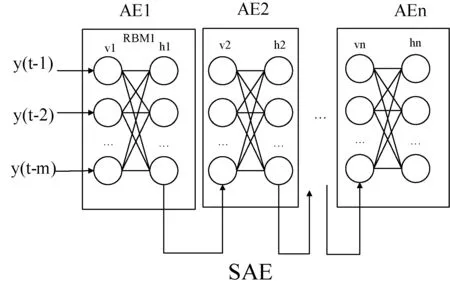
图2 栈式自编码器

SAE是对序列特征的学习过程，通过堆叠自编码器，对序列进行深度学习，可以表达出序列间的潜在特征。

对于实现时间序列的预测目标而言，则需要再添加一个用于预测目标的神经元，这一神经元的目的在于通过监督学习调整网络模型以此实现预测目标。

1.3SAEP模型

对于时间序列{y(1),y(2),…,y(n)}，通过添加神经元，在t时刻基于SAE的时间序列预测模型SAEP(StackedAutoEncoderbasedPredictionmodel)结构如图3所示。

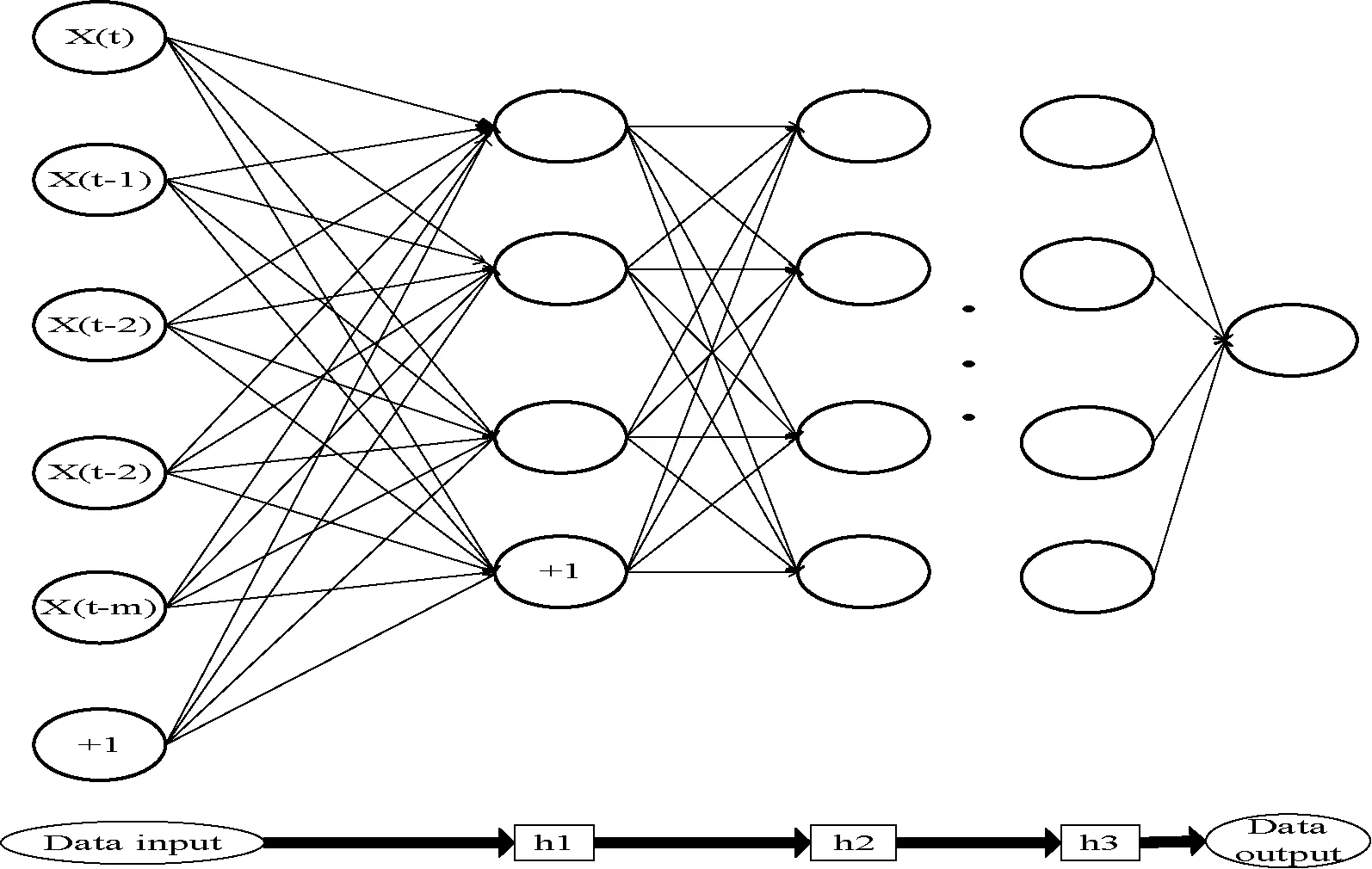
图3 SAEP的结构

对于栈式自编码神经网络，第1层的编码器隐层特征为：

h(l)=σ(W(l)h(l-1)+b(l))

(5)

其中，h(0)=Y,W(l)和b(l)分别表示第1层自编码器的编码层权重和偏置。通过自编码器的栈化多次非线性变换得到的h(n)表示了网络学习到的潜在特征，它包含了预测目标中的重要信息。为了达到预测目标，以非线性sigmoid神经元作为最后预测模型的输出节点。

SAEP模型的整体代价函数为：

(6)

SAEP的关键是不断调整{w,b}以此拟合出输入输出数据之间的函数关系。

2 SAEP模型的学习算法

基于以上的模型构建，SAEP的特征学习过程可以分为无监督的预训练，即SAE的特征学习，这一过程旨在挖掘出输入序列的深层特征；基于监督学习的预测，即深度神经网络的扩展(SAEP的构建)及网络微调。

2.1 自编码器的学习算法

自编码器的参数学习采取反向传播算法。在优化神经网络时，首先利用式(1)和式(2)计算各层的神经元激活值，根据式(3)计算代价函数，利用反向传播算法计算各层代价函数的偏导数。假定自编码器的输出层为第L层,输出目标为Y，自编码器的输出层和隐藏层各个节点的误差表达式分别为：

δ(L)=-(Y-σ(z(L)))f′(z(L))

(7)

(8)

其中，l=L-1,…,2，式中的f为sigmoid函数，f′(z(l))表示第l层激活函数f(z)对输入z的导函数值。按照下式计算l层神经元节点的激活值：

z(l)=w(l)h(l-1)+b(l)

(9)

然后，根据以下公式计算需要的梯度：

▽w(l)E(W,b;x,y)=δ(l+1)(h(l))T

(10)

▽b(l)E(W,b;x,y)=δ(l+1)

(11)

利用梯度下降法更新权重参数，设α为每次迭代的学习率，迭代更新表达式为：

w(l)=w(l)-α[▽w(l)E(W,b;x,y)]

(12)

b(l)=b(l)-α[▽b(l)E(W,b;x,y)]

(13)

通过不断反复迭代以此减小代价函数式(3)的值，以此来优化自编码器。

2.2 逐层贪婪学习算法

栈式自编码器若采取梯度下降法，往往并不能取得很好的效果，主要原因在于网络深度的增加会使得反向传播的梯度值急剧减小，因此在最初的几层网络权值的导数非常小，即权值变化非常缓慢，以至于无法训练[15]。为避免训练出现局部最优，SAE的实现采取逐层贪婪学习算法[15]。该算法的主要思想在于每次只训练网络中的一层，首先训练一个只含一个隐藏层的自编码器，该层自编码器达到优化后再开始训练下一个自编码器。利用逐层贪婪学习算法完成SAE无监督预训练。

2.3SAEP微调

无监督预训练之后，如图3所示构建SAEP模型，微调策略为监督学习机制。微调以图3为网络结构模型，将所有层视为一个网络整体，以SAE预训练结果为初始权值。利用式(5)、式(6)前向传播计算各个层神经元节点的激活函数值和整体代价函数，再利用反向传导算法计算式(7)-式(13)(此时式(8)的β=0，其他相应的损失函数为J(w,b)),通过反复迭代梯度下降法更新权重参数，以此使得SAEP的代价函数式(6)达到最小。

3 实验设计与分析

此次实验的软件平台为MATLABR2014a，编程实现算法。

模型的评价标准为式(14)、式(15)表示的均方偏差、平均偏差率。

(14)

(15)

实验数据来源于经典数据库TimeSeriesDataLibrary，来源于真实的金融市场(https://datamarket.com/data)。8个数据集为1979年12月31日—1998年12月31日JPY/USD(日本/美国)、French/US(法国/美国)、German/US(德国/美国)、Australia/US(澳大利亚/美国)、British/US(英国/美国)Canadian/US(加拿大/美国)、Dutch/US(荷兰/美国)、Swiss/US(瑞士/美国)汇率时间序列。

实验中，对所有实验数据均按式(16)进行[0,1]上的归一化预处理。然后采取单变量滑动窗口机制训练数据，样本总数为4 774，随机抽取80%作为训练样本，20%作为测试样本。本次实验在不同数据集模拟20次，并对测试集结果取平均值。

(16)

表1为在不同数据集下SAEP的预测效果。从表中可看出，模型的预测误差均控制在较低的水平，其预测耗时均在1 s以内，能够很好地满足实时预测中对预测时间和预测精度的高要求。此外，在实验中算法在不同的数据集下均能够保证100次以内得到收敛，收敛较快的特点保证了模型在不同数据集的稳定性。

表1 不同数据集的测试集预测效果

续表1

为了充分反应模型的效果，以日/美测试数据集为例，对比目前在汇率时序预测中得到普遍应用的BP神经网络和SVR。如表2所示。

表2 不同预测模型的测试预测效果

不难发现，SAEP的预测效果优于BP神经网络和SVR。BP神经网络被证明可以以任意精度逼近任意的函数，但其随机初始化时导致结果不够稳定，泛化能力表现欠佳。通过三种模型的对比可以看出，SAEP的表现能力更强。

4 结 语

栈式自编码器预测模型改进了神经网络随机初始化的缺点，有效地表达出序列数据间非线性及随机性的特点，自编码器在神经网络的预训练对于提高预测效果具有重要意义；SAEP的微调作用以监督机制通过反向传导算法调整网络，这对于预测目标起到了关键的作用，无监督学习对于时间序列的实时预测具有重要的应用研究和推广价值。

但是反向传导算法在网络层次过深时会出现梯度扩散现象，因此本文提出的栈式自编码预测模型更适合于低配置计算资源中网络层次不是特别深的预测中。

[1] 刘金培,林盛,郭涛,等.一种非线性时间序列预测模型及对原油价格的预测[J].管理科学,2011,24(6):104-122.

[2]MartinLangkvist,LarsKarlsson,AmyLoutfi.Areviewofunsupervisedfeaturelearninganddeeplearningfortime-seriesmodeling[J].PatternRecognitionLetters,2014(42):11-24.

[3] 王知音,禹龙,田生伟,等.基于栈式自编码的水体提取方法[J].计算机应用,2015,35(9):2706-2709.

[4]BengioY,CourvilleA,VincentP.LearningdeeparchitectureforAI[J].FoundationsandTrendsinMachineLearning,2009,2(1):1-127.

[5] 邓侃,欧智坚.深层神经网络语音识别自适应方法研究[J].计算机应用研究,2016,7:52-56.

[6] 周慧,周良,丁秋林.基于深度学习的疲劳状态识别研究[J].计算机科学,2015,42(3):191-200.

[7] 姚利涛,董育宁.无监督的视频业务特征分析与分类[J].应用科学学报,2015,33(2):117-128.

[8]SantoAAP,CostaJNCA.Computationalintelligenceapproachesandlinearmodelsincasestudiesofexchangerate[J].ExpertsSystemswithApplications,2007,33(4):816-823.

[9]EtteHarrisonEtuk.AseasonalARIMAmodelfordailyNigerianNAIRA-USDollarexchangerates[J].AsianJouralofEmpiricalResaerch,2(6):219-227.

[10]MichaelMckenzie,HeaherMitchell.GeneralizedasymmetricpowerARCHmodellingofexchangeratevolatility[J].AppliedFinancialEconomics,2002,12(8):555-564.

[11] 刘潭秋,谢赤.基于GRACH模型和ANN技术组合的汇率预测[J].科学技术与工程,2006,6(23):4690-4694.

[12]ChenAS,LeungM.RegressionNeurralNetworkforErrorCorrectioninForeignExchangeForecastingandTrading[J].Computers&OperationsResearch,2004,31(7):1049-1068.

[13]ChakradharaPanda,VNarasimhan.ForecastingExchangeRateBetterwithArtificialNeuralNetwork[J].JournalofPolicyModeling,2007,29(2):227-236.

[14]CaoLJ.Supportvectormachinesexpertsfortimeseriesforecasting[J].Neurocomputing,2003,51:321-339.

[15]HintonGE,OsinderoSYW.TheAfastlearningalgorithmfordeepbeliefnets[J].NeuralComput,2006,10(7):1527-1544.

EXCHANGE RATE TIME SERIES PREDICTION BASED ONSTACKED AUTOENCODER MODEL

Kou Xixi1He Xiping1,2,3*

1(ChongqingKeyLaboratoryofElectronicCommerceandSupplyChain,ChongqingTechnologyandBusinessUniversity,Chongqing400067,China)2(SchoolofComputerScienceandInformafionEngineering,ChongqingTechnologyandBusinessUniversity,Chongqing400067,China)3(ChongqingDetectionControlIntegratedSystemEngineeringLaboratory,ChongqingTechnologyandBusinessUniversity,Chongqing400067,China)

Aiming at the current problem of limited prediction accuracy of nonlinear financial time series in the shallow model, a novel prediction model of stacked autoencoder neural networks is proposed, consisting of stacked autoencoder model at the bottom and regression neurons at the top. First of all, the unsupervised learning mechanism of autoencoder is applied to identify and learn the features of time series, greedily learning the neural network layer by layer. Then the stacked autoencoder is extended to be the SAEP model with supervision mechanism, and the parameters learned by SAE (stacked autoencoder) are used to initialize the neural network. Finally, the weights are fine-tuned by supervised learning. The experimental design uses the exchange rate time series as the training and test samples, and the effectiveness of the proposed model in the application of exchange rate time series prediction is verified, compared with the more mature methods.

Time series Prediction Deep learning Stacked autoencoder Feature learning Deep neural networks

2016-03-02。重庆市教委科技

KJ1400612)；重庆工商大学研究生院“创新型科研项目”(yjscxx2015-41-21)。寇茜茜，硕士生，主研领域：机器学习。何希平，教授。

TP391 TP183

A

10.3969/j.issn.1000-386x.2017.03.039