飞机平尾着陆滑跑动态性能分析

秦 飞 ∕

(上海飞机设计研究院，上海201210)

飞机平尾着陆滑跑动态性能分析

秦 飞 ∕

(上海飞机设计研究院，上海201210)

飞机着陆滑跑过程中，平尾结构将受到较大的冲击作用和振动激励。为预判结构局部危险部位，给结构强度设计提供参考，需对平尾着陆滑跑过程中的动态性能进行分析。创新性地考虑了飞机滑跑速度和气动力的变化，为有限元计算提供可靠的外载输入，并合理设置约束条件，建立半机体有限元模型，降低计算规模。最后提取平尾各站位处的载荷响应峰值，作出动响应包线，预判结构局部危险部位，如平尾根部，为结构强度设计提供参考。

平尾；结构；着陆；滑跑；动态性能

0 引言

飞机结构在使用过程中常常受到各种各样的动载荷作用，这些动载荷可能会引起结构的动强度破坏。随着飞机性能的逐步提高，振动激励和冲击作用也越来越强烈，其所造成的危害程度的大小与飞机的运动状态、环境以及飞机结构本身的动态特性密切相关。所以，一架飞机从开始设计直到退役，在这一过程中结构动强度是必须予以高度关注的问题[1]。本文主要针对振动故障类型中的振动峰值破坏进行研究。

飞机平尾在着陆滑跑过程中动响应分析涉及两个方面的内容：(1)起落架动态性能的分析；(2)飞机平尾的有限元动响应分析。对于起落架的动态性能分析，W Karam等[2]和Kapseong Ro[3]做过起落架模型的落震仿真，Karen H. Lyle等[4]研究坠撞过程，验证了在机身未损毁前使用刚性机体模型的合理性，Phil Evans等[5]利用MATALAB/SIMULINK模拟飞机起飞和着陆过程。对于有限元分析模型，波音公司在上世纪50年代采用三角元对平尾进行建模，极大地推动了有限元法的发展和使用[6]。目前应用最广泛的通用有限元商用软件有ABAQUS，ADINA，ANSYS，MARC，NASTRAN和SAP等[7]。徐焱[8]、孟庆贺[9]等人成功运用MSC. PATRAN& NASTRAN等软件，对机体动响应做了相应的研究，但主要是针对机身上个别点，所给出的响应的时间历程响应曲线，有一定的局限性。

本文在前人研究基础上，利用现在流行的CAD技术，采用ADAMS进行模拟仿真，求得在着陆滑跑过程中起落架对机体的激振力，为下一步计算机体动响应打好基础。在对空气动力问题的处理上，本文与以往的研究方法不同，未采用陈旺[10]的等效升力法，而是对ADAMS进行二次开发，通过编写ADAMS GFOSUB子程序来解决。这样能真实地模拟飞机在着陆滑跑过程中机体上气动力的变化，仿真过程和实际情况更接近，计算结果更准确。飞机平尾作为一个整体，如果只计算个别站位上的动响应，很难判断危险截面所在部位，为飞机强度设计提供的参考价值相对有限，为克服这一缺陷，本文计算了平尾上所有站位处的弯矩、剪力和扭矩。通过对各站位处动响应值的筛选，提取响应峰值，以站位位置为横坐标，响应峰值为纵坐标，作出动响应包线[11]。本文根据这一思想，提取各站位处的响应峰值，作出相应的包线，并进行分析，为飞机平尾强度设计提供较好的参考。

1 起落架动力学建模

1.1 动力学模型

目前在起落架动态性能力学模型中普遍采用由弹性与非弹性支撑质量组成的二质量模型[10]。弹性支承质量，即缓冲器中空气弹簧的上部质量，包括机身、机翼、尾翼、缓冲器外筒等质量，即空气弹簧支承的质量。非弹性支承质量，即空气弹簧下部的质量，包括缓冲器活塞杆、刹车装置、轮胎等质量，对于小车式起落架还要包括车架，即非空气弹簧支撑的质量。

对于缓冲支柱式起落架考虑将气体腔和油液腔分别等效为一个弹簧力和一个阻尼力。缓冲支柱力由空气弹簧力、油液阻尼力、缓冲器摩擦力和结构限制力组成。一旦起落架的几何参数和初始充填参数确定，则油-气式缓冲支柱的各个力即可确定。轮胎力随轮胎压缩量而变化，各分力的具体表达式可参见文献[10]。

1.2 起落架系统建模

在ADAMS/AIRCRAFT模块中，仿真模型都是以模板为基础的，前起落架缓冲支柱和机轮子系统以及主起落架缓冲支柱和机轮子系统可以调用软件自带的模板。为了使所建模型与实际情况更接近，需要根据某型飞机缓冲支柱的初始容积，初始压力，活塞面积，油孔面积，缓冲支柱行程和轮胎垂直变形系数及阻尼系数等参数，利用文献[10]中力的表达式，修改空气弹簧力、油液阻尼力、缓冲器内部摩擦力、结构限制力和轮胎力等属性文件。属性文件编写准确与否直接决定了仿真结果的优劣，所以这是前期工作的重点。在子系统都建成之后，分别装配成前起落架系统和主起落架系统，进行落震仿真，验证所建起落架模型的准确性或合理性。

1.3 起落架落震仿真与验证

落震仿真是为了验证所建起落架模型的准确性，通过仿真和实验结果进行对比，达到验证目的。首先，确定前起落架和主起落架的支撑质量，可以通过力和力矩平衡关系确定。例如，已知某飞机全机质量47 681kg，停机状态飞机重心至前轮轮轴的水平距离9.116m，至主轮轮轴的水平距离0.960m，可以求出前起落架支撑质量为4 543kg，主起落架支撑质量为43 138kg。

确定了支撑质量后就可以对飞机的前起落架和主起落架分别进行落震仿真，下沉速度均为3m/s，姿态水平，仿真时间6s，仿真时间步数600。仿真结果和实验结果[10]的对比如表1所示，各主要参数相对误差均在5%以内，根据工程经验，可见所建的起落架模型和实际情况吻合的较好。

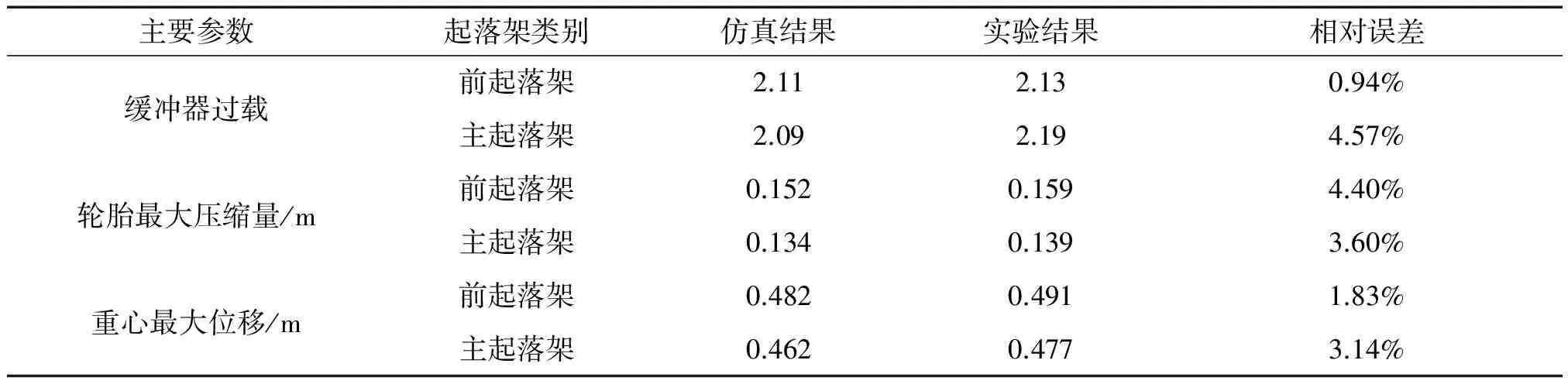
表1 前起落架和主起落架仿真结果与实验结果的对比

2 全机多体系统动力学建模

虚拟样机分析模型不一定与实际模型的形状完全一致，适当的模型简化是必要的，只要虚拟样机分析模型的工况符合实际工作的工况即可。基于这种思想，利用MSC.ADAMS建立全机多体系统模型。

在建立并验证了前、主起落架系统模型的基础上，调用刚性机体模型。文献[4]表明，使用刚性机体是可行的。根据起落架和机体实际的连接位置，修改相关几何参数，最后装配成全机模型，进而进行滑跑和着陆仿真分析。

3 着陆滑跑仿真

3.1 路面谱

由于路面不平度的影响，飞机在跑道上滑行时会引起振动，这对于起落架的疲劳寿命起重要作用，同时会影响飞行员的正常工作和乘客的舒适性。另外，滑行载荷的累积影响在飞机总的疲劳损伤中也占有一定的比例，不能忽略。因此，需要选择合适的路面谱，对飞机在滑行过程中的振动进行模拟仿真，以便掌握飞机滑行中起落架的动力学响应特征。

为了较好地模拟飞机着陆滑跑的真实情况，本文使用适航当局认可的San Francisco 28R跑道进行仿真。该跑道修建于上世纪60年代前期，路面较粗糙，飞机在该跑道上着陆滑跑将受到较高的激励载荷[12]。此跑道的路面谱是根据实测结果编制的，适用于模拟实际跑道。

3.2 着陆滑跑仿真分析

着陆过程是飞行剖面最危险的阶段之一，研究这一过程具有重要意义[5]。本文着重研究飞机刚触地后进行滑跑的动态过程。由于飞机着陆时水平速度较大，机体上附加作用较大的气动升力，刚触地的那一瞬间甚至可以达到0.8～0.9倍的全机总重[13]，因此在仿真过程中气动升力不可忽略。

对于随时间变化的气动力的添加，可以通过编写的ADAMS GFOSUB子程序实现。首先定义用户界面，然后建立用户求解库。只有这样，用户子程序才能连接到ADAMS/SOLVER求解，接着编写气动力子程序GFOSUB。气动力与机翼迎角、飞机速度和气动面积等参数相关。关于这些参数，可参见文献[14]。作用于机翼的气动升力表达式如下：

(1)

式中，CL为升力系数(与机翼迎角有关)，S为机翼参考面积，q为动压，定义式如下：

(2)

式中，ρa为空气密度，Va为气流速度。

由以上两个公式可以看出，气动力随机翼迎角和气流速度变化，子程序可以将变化的气动力加到机身上。将编好的气动力子程序添加到机身模板中，建立机身子系统，最后将前面建好的前起落架和主起落架子系统，结合机身子系统，建立全机模型，进行着陆仿真。

着陆滑跑可以作为匀减速运动处理，平均加速度表达式如下[13]：

(3)

式中， f为机轮对地面的摩擦系数，取0.3；Kjd为接地瞬间飞机的升阻比，取6.95。由此计算可得平均加速度为-2.175m/s2。

将建好的前起落架和主起落架模型，加上自定义气动力的机身装配成全机模型，输入SanFrancisco28R跑道路面谱，进行滑跑仿真。水平速度为66.6m/s，机身迎角3.5°，仿真时间为6s。在进行着陆仿真时选取两种典型情况进行分析，一种是正常着陆，另一种是极端的粗暴着陆，对应的下沉速度分别为1.22m/s和3.05m/s。参数设置完后提交到ADAMS/SOLVER求解器进行动力学分析计算。

着陆滑跑仿真时，气动升力随时间的变化曲线如图1所示。

在0s时刻，两种下沉速度对应的气动升力大小不同，如图1所示，下沉速度为1.22m/s时为3.83E+005N，是飞机总重的82%；下沉速度为3.05m/s时为4.16E+005N，是飞机总重的89%。可见后者比前者大，这是因为较大的下沉速度造成了较大的诱导迎角。0s时刻是主起落架刚刚触地的瞬间，此时全机的气动升力最大，由文献[13]可知，能达到0.8～0.9倍的全机总重，以上计算结果也说明了这一点，表明仿真结果是合理的。

4 动响应分析

4.1 有限元模型的建立

为减少结构的自由度数，提高计算的效率，本文利用结构的对称性条件，建立半机体模型，如图2所示。全机结构相对于XOY平面对称，对称面上结构元素的刚度和节点惯性数据均取一半。本文计算的是飞机对称着陆滑跑状态下，机体的结构动力学响应，所以在对称面上施加对称约束，即将对称面上节点的反对称位移限制为零：

(4)

式中，TZ为Z方向的节点线位移，RX和RY分别为X方向和Y方向的节点角位移，下标S表示对称面上的节点号。全机结构有限元模型具有386个等截面直梁元(bar)，246个质量元(mass)，20个刚性元(rigid)，2个弹性元(DOF Spring)。

4.2 外载荷的添加

机体对称着陆载荷由两大部分组成，一部分是着陆撞击前的平飞载荷，另一部分是起落架的撞击载荷和由它引起的机体惯性载荷。运用PATRAN将外载荷添加到半机体模型上，如图2所示。

4.3 动响应结果及分析

平尾弯矩矢量为X向，剪力为Y向，扭矩矢量为Z向，平尾各站位所对应的节点号为Node 401～411，其中飞机对称面与平尾轴的交点为横坐标原点(0m)，Node 411作为终点(5.698m)，Node 401在Z方向的坐标为1.598m，提取该站位处弯剪扭的响应峰值，作出动响应包线，如图3～5所示。

平尾和升降舵之间通过刚性元(rigid元素)及旋转弹簧元(DOF Spring元素)连接，连接点为Node 402和Node 410两点，在Z方向距离原点分别为1.998m和5.273m。平尾弯矩在根部最大，越往翼尖，弯矩越小。如图3所示，下沉速度1.22m/s和3.05m/s对应的弯矩最大值分别为2.71×104N·m和3.95×104N·m；又，下沉速度3.05m/s对应的平尾各站位弯矩也均比1.22m/s的大。由于升降舵的作用，在其与平尾的连接点附近，即在站位1.998m和5.273m附近，平尾剪力和扭矩的变化曲线出现“折点”，如图4和图5所示；下沉速度1.22m/s和3.05m/s对应的剪力最大值分别为0.85×104N和1.29×104N，扭矩最大值分别为4.06×103N·m和7.24×103N·m。

由以上计算结果，可以清晰地看出平尾结构的局部危险部位，即各部件较高载荷集中处，如平尾根部，因此需要对此部位进行加强设计，以便为整架飞机的结构完整性提供保障，因而具有明显的实际意义。

5 结论

通过上述计算分析，可以得出以下结论：

1)飞机着陆滑跑过程是一个动态变化过程，飞机升力和滑跑速度会发生动态变化，本文考虑了这两个因素，能更合理地反映飞机着陆滑跑过程中起落架的动态性能, 为有限元分析提供更可靠的外载输入。

2)运用Patran软件将前起落架支柱力、主起落架支柱力、气动升力和全机重力等外载荷施加到半机体有限元模型上，提交Nastran进行计算，最后提取平尾各站位处的载荷响应峰值，作出动响应包线，确定各部件载荷的最大值，预判结构局

部危险部位，如平尾根部，为结构强度设计提供参考。

[1] 曾宁.结构动力学在飞机设计中的应用技术研究[J].西南交通大学学报，2002，37(11)，增刊：110-112.

[2] W Karam and J-C Mare. Advanced model development and validation of landing gear shock struts[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering 2010，224: 575-586.

[3] Kapseong Ro. A Descriptive Modeling and Simulation of Aircraft-Runway Dynamics[C]. 44th AIAA/ASME/ASCE/AHS Structures, Structural Dynamics, and Materials Conference, Norfolk, Virginia, 7-10 April 2003: 1-11.

[4] Karen H. Lyle, Karen E. Jackson and Edwin L. Fasanella. Simulation of Aircraft Landing Gears with a Nonlinear Dynamic Finite Element Code[J]. Journal of Aircraft, January-February 2002, Vol. 39, No: 142-147.

[5] Phil Evans, Mario G. Perhinschi, and Steven Mullins. Modeling and Simulation of a Tricycle Landing Gear at Normal and Abnormal Conditions[C]. AIAA Modeling and Simulation Technologies Conference, Toronto, Ontario Canada, 2-5 August 2010:1-20.

[6] 王富耻，张朝晖.ANSYS10.0有限元分析理论与工程应用[M].北京：电子工业出版社，2006年：1-2.

[7] 江见鲸，何放龙，何益斌，等.有限元法及其应用[M].北京：机械工业出版社，2006：1-7.

[8] 徐焱.飞机带翼尖弹着陆响应研究[J].飞机设计，2003(1)：27-32.

[9] 孟庆贺.飞机着陆撞击与滑跑响应分析[D].南京：南京航空航天大学，2007.

[10] 陈旺.小车式起落架落震及全机着陆动态仿真分析[D].南京：南京航空航天大学，2005.

[11] 《飞机设计手册》总编委会.飞机设计手册第9册：载荷、强度和刚度[M].北京：航空工业出版社，2001：111-129.

[12] Donald Freund, Douglas R. McKissack, Laurence C. Hanson. Dynamic Taxi, Take-Off and Landing Roll Analyses for Large Business Jet Aircraft[J]. American Institute of Aeronautics and Astronautics, 3-6 April 2000, A00-24567:1-11.

[13] 熊海泉，刘昶，郑本武.飞机飞行动力学[M].北京：航空工业出版社，1990：86-88.

[14] 常振亚.飞机飞行性能计算手册[M].陕西：飞行力学杂志社，1987：255-261.

Dynamic Performance Analysis of Aircraft Horizontal Tail When Landing and Taxiing

QIN Fei

(Shanghai Aircraft Design and Research Institute, Shanghai 201210, China)

The horizontal tail structure suffers large impact and vibration in landing and taxiing. For predicting the structure local hazard areas, it is necessary to implement an analysis on horizontal tail dynamic performance in landing and taxiing in order to provide a reference for structural strength design. This paper innovatively considered about changes of airplane taxiing rate and the aerodynamic force to provide a reliable set of external input, set reasonable constrains, and established half-body finite element model of airplane to reduce the size of the calculation. Finally, the peak load response at each horizontal tail station was extracted to generate dynamic response envelope, so the local hazardous positions can be pre-estimated to provide references for the structure design, such as the root of horizontal tail.

horizontal tail; structure; landing; taxiing; dynamic performance

10.19416/j.cnki.1674-9804.2017.01.011

V212.13

A