判别金属材料疲劳试验中异常试验数据的一般方法

唐兆田 /

(上海飞机设计研究院，上海201210)

判别金属材料疲劳试验中异常试验数据的一般方法

唐兆田 /

(上海飞机设计研究院，上海201210)

在金属疲劳试验中，有时会出现一个或多个明显小于或大于其它数据的异常数据。查找导致这些异常数据的原因是很困难的，难以直接剔除。通常，相关文献只简要地提供基于统计学的识别异常数据的判据。为了帮助数据分析人员更好地理解这些统计判别方法，在处理金属疲劳试验数据时更好地运用统计判别方法，对分布于各文献中的统计判别法进行了归纳整理，并给出必要的推导过程和公式，最后对所列统计判别法进行总结，介绍各方法的优势和不足，并给出建议。

疲劳试验；异常数据；粗大误差；统计方法

0 引言

目前，民用飞机结构中仍然广泛采用金属材料，通常不低于50%，甚至在将来很长时间内金属材料都将在民用飞机结构中发挥举足轻重的作用。随着新材料、新设计、新工艺等应用在民用飞机结构上，基于对飞机安全性、经济性、耐久性的考虑，需要进行大量疲劳试验以获得金属材料的相关疲劳性能数据。

相对于静力试验，疲劳试验数据具有较大的分散性，通常要求一组试验中有较多的试验件，通过对一组试验数据的统计分析获得所需疲劳性能数据。根据观察，偶尔出现一组疲劳试验数据中存在一个甚至多个与其它数据有明显差异的数据，即异常数据。异常数据会对试验结果产生明显的歪曲，甚至会导致错误的结论[1-2]。

正常情况下，每个试验数据中包含三个部分：真值、偶然误差、系统误差[1]。通常将误差分为三类，即系统误差、偶然误差和粗大误差[2-3]。系统误差的特点是，在相同的条件下，系统误差对测量数据的影响具有规律性，有很多文献讨论了系统误差的识别和消除[4-7]。偶然误差(随机误差)由未知或不可控的微小因素综合作用造成的，具有随机性和抵偿性[8]。粗大误差是由某些突发的异常因素造成的，没有规律性，通常对测量数据影响显著[9]。含有粗大误差的数据为异常数据[10]，对可能含有粗大误差的数据称为可疑数据。

对待可疑数据，若为得到较好的测量结果而无充分依据地轻率剔除，则得到虚假的测量结果；若无原则地作为正常数据而保留，则降低了测量的准确度[11]。一般采用物理判别法或统计判别法对可疑数据进行判别，以确定是否为可疑数据[6]。

物理判别法指根据对客观规律的认识来判定异常数据，识别导致异常数据的原因，并进行剔除；统计判别法指采用统计方法判定可疑数据是否由偶然误差造成，如果不是，即认为是由粗大误差造成，并进行剔除。在实践中，试验人员通常信任物理判别法，但是试验中有时出现异常数据而原因不明，物理判别法很难奏效，因此只能采用统计判别法来判定异常数据[12]。很多关于试验数据处理的文献给出了不同的统计判别法，但是都相对零散，且通常仅给出各种方法的判据和速查表、倾向于方法的运用。为了帮助试验人员或设计人员更好地理解常用的统计判别方法，在处理金属疲劳试验数据时更好地运用统计判别方法，本文对分布于各文献中的统计判别法进行了归纳整理，并针对某些方法给出必要的推导过程和公式，最后对所列统计判别法进行总结，介绍各方法的优势和不足，并给出建议。

1 判别异常数据的统计方法

1.1 拉依达(Paǔta)准则法

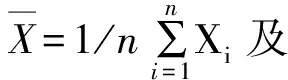
(1)

判据如下：

只有当所有观测值均落于X±3σ区间内时，剔除测量数据的犯错概率随着n的增大而减小，最后稳定于0.27%(X±3σ区间内累积概率为0.997 3，有文献近似地取0.3%)，应用拉依达准则才是零风险的。当有k个观测数据位于X±3σ区间外，即存在k个异常数据的概率为[15]：

(2)

随着异常数据数量的增加，在一定样本量范围内有用测量数据被剔除的风险也是逐渐增大的。

1.2 肖维纳(Chauvenet)准则法

假设多次重复测量所得n个测量数据中，数据残差为|vi|>ZcS，则剔除此数据。

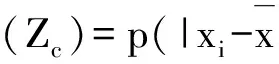
p和Z的下标c表示用于肖维纳准则：

(3)

(4)

Zc由φ(Zc)查正态概率积分表确定，而按照式(4)φ(Zc)又决定于n值，因此可得表1。

n=185时Zc=3，但实际应用中n<185即Zc<3，因此肖维纳在一定程度上弥补了拉依达(Paǔta)准则的不足；但是，从理论上考虑，当n→∞时p→0，所有异常数据都无法剔除，n和Zc的关系如图1所示。

表1 肖维纳准则Zc值表

1.3 格拉布斯(Grubbs)准则法

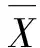
因此有如下的判别准则[15]：

(5)

则可疑数据Xd含有粗大误差，应予剔除；否则，应保留。

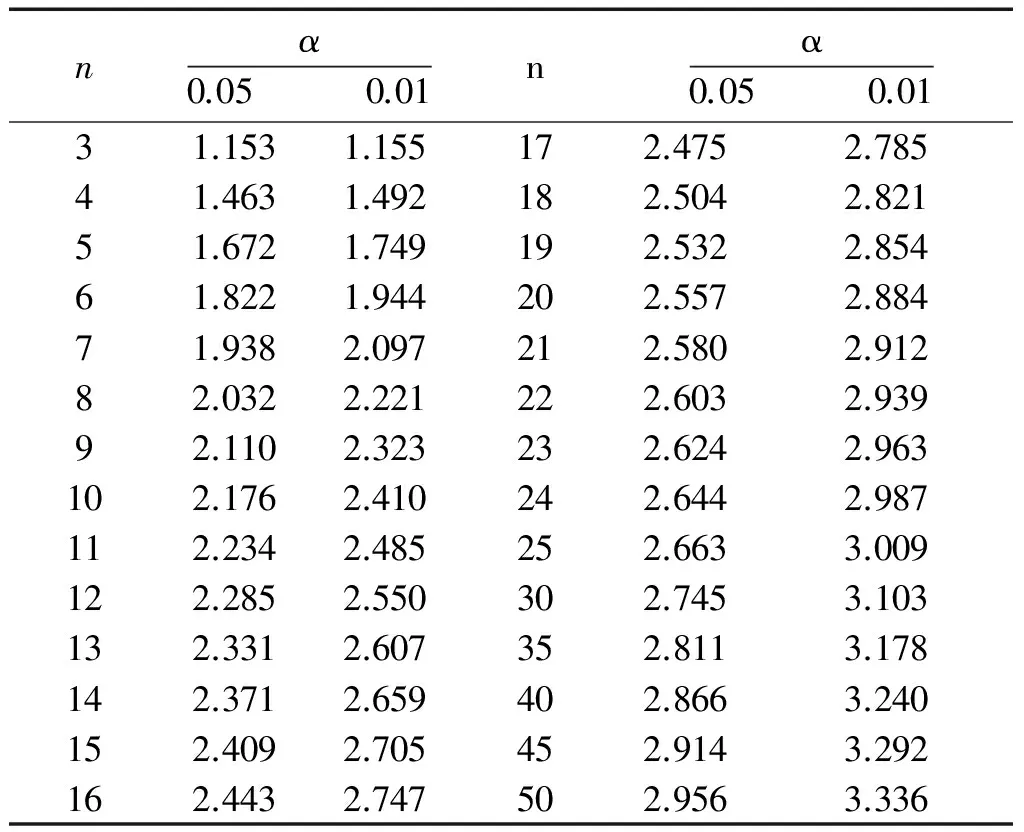
一般计算时，可以利用表2速查G(α,n)值。

表2 格拉布斯(Grubbs)准则的临界值G(α,n)

nα0．05 0．01nα0．05 0．0131．1531．155172．4752．78541．4631．492182．5042．82151．6721．749192．5322．85461．8221．944202．5572．88471．9382．097212．5802．91282．0322．221222．6032．93992．1102．323232．6242．963102．1762．410242．6442．987112．2342．485252．6633．009122．2852．550302．7453．103132．3312．607352．8113．178142．3712．659402．8663．240152．4092．705452．9143．292162．4432．747502．9563．336

在仅有一个异常数据时，该准则剔除异常数据的效率较高。为了便于使用，本文归纳如下：

(6)

式中：

表2所列数据可用式(6)中单边检验公式计算获得。

1.4 狄克逊(Dixon)准则(Q检验)法

设正态测量总体的一个样本，按大小顺序排列为X1≤X2≤…≤Xn，构造检验高端异常数据Xn和低端异常数据X1的统计量，分为以下几种情况：

(7)

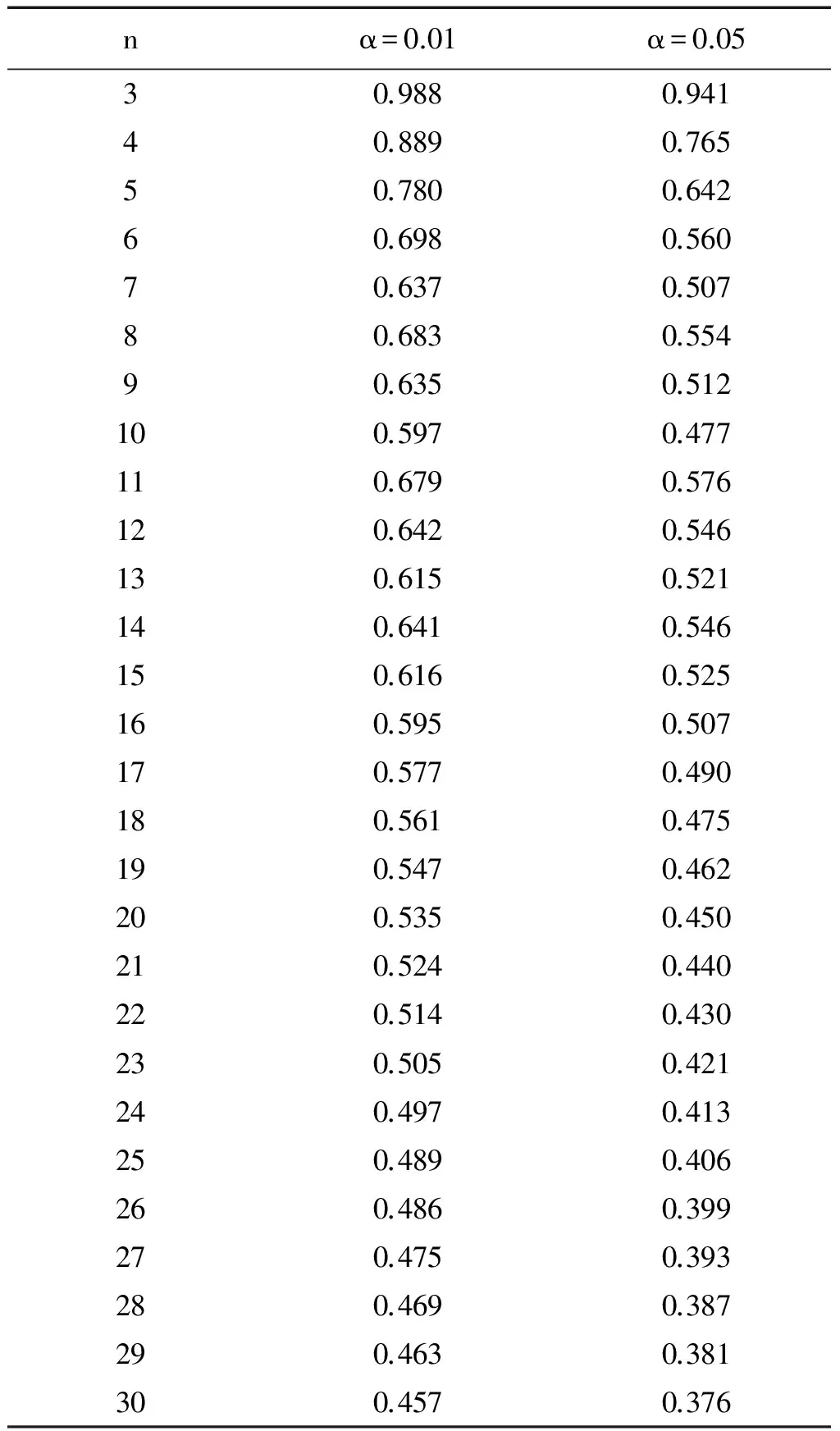
表3 狄克逊(Dixon)准则D(α,n)值表

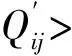
1.5 罗马诺夫斯基准则(t检验准则)法

罗马诺夫斯基准则是按t分布的实际误差分布范围来判断粗大误差，这对重复测量次数较少的情况比较合理。

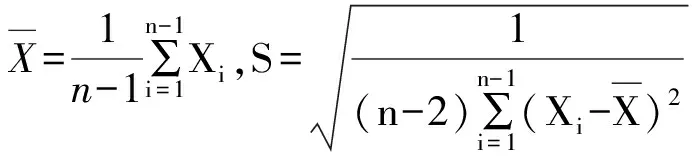
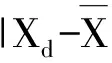
表4 罗马诺夫斯基准则K(α,n)值表

K(α,n)是与置信度(1-α)×100%和n有关的系数。

(8)

式中，tα(n-1)为t分布参数，可以根据α和(n-1)查t分布表。

2 结论

拉依达准则法最简单，无需查表，使用方便，测量次数较多或要求不高时比较适用，当测量次数小于或等于10时，拉依达准则法失效。肖维勒准则法是比较经典的方法，也是这五个方法中最古老的一个，它弥补了拉依达准则的不足，缺点是测量数据n无穷大时，该准则失效。肖维勒准则法和拉依达准则法的前提是测量数据和偶然误差符合正态分布，这两种方法都没有固定的概率意义[18]，带有一定的经验性。

狄克逊准则法[19-20]是在一定置信度和概率的条件下判别异常数据，该方法也是源自正态分布[21]，对数据中只存在一个或多个异常数据时，效果良好[22]，但缺点是当数据中异常数据的个数不止一个且出现在同侧时，该方法的检验效果不好，尤其同侧的异常数据很接近时效果更差，容易产生屏蔽效应；另一个问题是Dixon仅计算出了n≤30的D(α,n)值，D(α,n)值依赖查表，通用性不佳，如果测量数据大于30个建议按文献[23]选值。

格拉布斯准则法与罗马诺夫斯基准则法均以t分布为基础。在测量数据较少时罗马诺夫斯基准则法相对保守，但是该方法犯“弃真”错误的概率将

随着样本量的增加而增加，图2所示。格拉布斯准则法和狄克松准则法给出了严格的结果，有文献进行了比较，格拉布斯准则法效果最好[24]。可以通过重复使用格拉布斯准则法来判别多个异常数据，但同样也存在屏蔽效应，屏蔽效应是由于存在多个异常数据影响了均值而产生的，这与狄克逊准则法不同。

基于上述分析，本文以某金属材料DFR试验数据为例进行异常数据判别，供参考。105循环对应的最大应力(单位ksi)为20.42，20.43，20.40，20.43，20.42，20.43，20.39，20.30，20.40，20.43，20.42，20.41，20.49，20.39，20.39，20.4，其中20.30、20.49为可疑数据。分别采用上述方法进行异常数据判别，进行两轮判别，第二轮是在第一轮已经判别出异常数据的基础上、并剔除了异常数据(20.30)后进行的，见表5。

表5 算例

但是在金属疲劳试验中，应当注意到上述方法不是总有效[25]，因为上述方法均以测量数据按对称性概率分布(正态分布、t分布)为前提的，而金属疲劳试验的测量数据符合非对称的威布尔分布。以金属疲劳寿命试验为例，有时这两类分布模型都可以用于测量数据的分析，但是这两类分布模型主要差异存在于低寿命区和高寿命区，这两个区域正是异常数据发生的区域。有文献认为如果测量数据不符合正态分布，应采用非参数检验来判别异常数据，但是一般认为非参数检验没有参数检验可靠，而且通常要求样本量大于100甚至更多[26]。

因此本文建议在使用这些以对称性分布为前提的判别方法时，应当选择更严格的条件(如选择更小的值)。当样本较小且要求保守时，采用肖维纳准则法，简单快捷；拉格布斯准则法是国际上较为通用的方法，在条件允许的情况下，将拉格布斯准则法和狄克逊准则法组合使用，只要其中任何一种方法未判别为异常数据，就不能将可疑数据判别为异常数据，以降低犯“弃真”错误的概率。

[1] 韩承伟．科研资料的异常值及其处理[J]．内蒙古农业科技，1989(5)：37-40．

[2] 沙定国．实验误差理论与数据处理[M]．第一版.北京：北京理工大学出版社，1993：10-12，56．

[3] 刘兴胜，刘鹰．测量误差的表示方法及其分类[J]．计量与测试技术，2015(2)：37-40．

[4] 丁振良．系统误差的性质与评定方法[J]．哈尔滨工业大学学报，1985(4)：5-10．

[5] 樊士伟，易东云．系统误差的不确定性与参数估计精度折合[J]．弹道学报，2006(1)：30-34．

[6] 肖明耀．误差理论与应用[M]．第一版.北京：计量出版社，1985：28-34，169-176．

[7] 熊光楚．观测数据中系统误差的消除问题[J]．物探化探计算技术，2000(3)：193-199．

[8] 肖明耀．实验误差估计与数据处理[M]．第一版.北京：科学出版社，1980：12-14，56．

[9] 杨建潮．测量误差及粗大误差的判别与消除[J]．计量与测试技术，2006，33(11)：4-5．

[10] 李梦奇，白晓军，匡同春，成晓玲，向雄志，黄应钦，雷淑梅．工程技术领域等精度数据异常值判定系统[J]．计量技术，2006(3)．

[11] 杨峰，李天柁，王哲．核物理实验中粗大误差的计算机处理[C]//全国第十二届核电子学与核探测技术学术年会论文集．中国云南昆明：中国电子学会核电子学与核探测技术分会、中国核学会核电子学与核探测技术分会，2014：445．

[12] 梁晋文，陈林才，何贡．误差理论与数据处理[M]．第二版.北京：中国计量出版社，2001：51-57，58-61．

[13] 马美娟．贝塞尔公式推导的再研究[J]．佳木斯大学学报(自然科学版)，2011，29(2)：290-295．

[14] 张敏，袁辉．拉依达(Paǔta)准则与异常值剔除[J]．郑州工业大学学报，1997，18(1)：85．

[15] 普仕凡，韩旭，李智生，李钊．一种面向最大值指标的粗大误差处理方法[J]．无线电工程，2014(5)：78-79．

[16] Jerry Thomas．Monte Carlo Investigation of the Probability Distributions of Dixon's Criteria for Testing Outlying Observations[R]．AD688600，Aberdeen Proving Ground，Maryland：Aberdeen Research and Development Center，1969．

[17] W.J Dixon．Processing Data for Outliers [J]．Biometrics，Volume 9，No.1，1953：74-89．

[18] 林丽芬，肖化，吴先球．肖维勒准则和格拉布斯准则的比较[J]．大学物理实验，2012，25(6)：87．

[19] R.B Dean，W.J Dixon．Simplified Statistics for Small Numbers of Observation [J]．Analytical Chemistry，1951，Volume 23(4)：636-638．

[20] Dixon WJ Ratios Involving Extreme Values [J]．The Annals of Mathematical Statistics，1951，Volume 22(1)：68-78．

[21] Mahendra P. Verma，Mario Cesar Suarez A.．Dixon Test Critical Values：Acomputer Code to Calculate Critical Values for the Dixon Statistical Data Treatment Approach [J]．Journal of Statistical Software，2014，Volume 57，Issue 2：1．

[22] 邓勃．关于异常值的检验与处理[J]．大学化学，1995，10(4)：5-9．

[23] Surendra P. Verma，Alfredo Quiroz-Ruiz．Critical values for six Dixon tests for outliers in normal samples up to sizes 100, and applications in science and engineering [J]．Revista Mexicana de Ciencias Geológicas，2006，Volume 23，núm. 2：133-161．

[24] 邓勃．异常值的检验与处理方法[J]．化工标准化，1995，10(4)：6-22．

[25] 何平．剔除测量数据中异常值的若干方法[J]．航空计测技术，1995，18(1)：19．

[26] National Aeronautics and Space Administration．NASA-HDBK-8739.19-3．Measurement Uncertainty Analysis Principles and Methods [S]．Washington DC：NASA，2010．

General Methods for Outlier Detection in Metal Fatigue Tests

TANG Zhaotian

(Shanghai Aircraft Design and Research Institute, Shanghai 201210, China)

In metal fatigue tests, one or more outliers are observed at some time. It is hoped that the outliers are detected and can be rejected directly, but it’s difficult. Most papers about test data analysis just provide some brief criteria which are based on statistics. For better handling metal fatigue test data, this paper collects five rejection-criteria and presents some derivation and formulas. And it’s useful to get a better understanding of these methods for test data analysts. At the end of this paper, a summary is given, some advantages and disadvantages of these methods were introduced, and suggestions are also provided.

fatigue test;outlier;gross error;statistical method

10.19416/j.cnki.1674-9804.2017.01.016

V252

A