“用两条腿走路”学好勾股定理
湖北省鄂州市第五中学(436000) 孙孝娥 ●
“用两条腿走路”学好勾股定理
湖北省鄂州市第五中学(436000) 孙孝娥 ●
数学中的定理是数学思维和数学经验的高度抽象总结,对于同学来说晦涩难懂,同样对于老师来说教学难度大.勾股定理作为初中数学几何中的重点内容,是历来考试的重点和难点.我们发现单纯的理解定理的内容只能应用相对简单的题型,基于勾股定理考查变式多,与其他内容结合方式广的特点,要求同学们在理解定理的同时,更应掌握定理的变式,培养观察和识别定理应用要件的能力,学会转换和构建符合定理应用的逻辑思维.要做到以上这几点,就要求同学们学会“用俩条腿走路”,即从正反俩方面理解勾股定理,切实的掌握勾股定理及其逆定理的相关内容.
一、迈出第一步,理解勾股定理
勾股定理的总结源于对生活现象的好奇与理解,它科学地归纳了直角三角形三条边的数学关系——两条直角边的平方和等于斜边的平方.这就为求解与直角三角形相关的数学模型中的角度和边长提供了一种具体可行的方法.
例1 估算大楼的高度.张同学放飞一支风筝,当风筝飞到大楼的高度时,他发现自己恰好距离大楼约40米,收线后经过测量风筝线已经被放出了为50米.请估算大楼的高度.
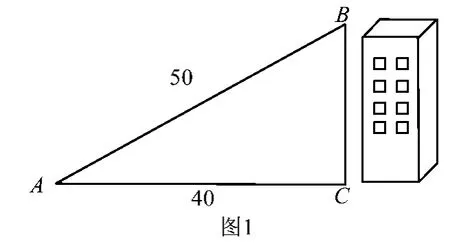
分析 根据题目的内容可以将以上情形构建为一个简单的直角三角形模型,如图1所示,则AB=50米,AC= 40米,求的大楼的高度为BC.根据勾股定理可得:AB2= AC2+BC2所以BC2=AB2-AC2=502-402=900,BC即大楼的高度约为30米.
在直角三角形这个模型框架中,由于勾股定理是对直角三角形特性的进一步剖析和总结,所以可以直接利用勾股定理来解决问题.掌握勾股定理的实质是学习这个定理的基础,有助于接下来应对直角三角形的证明、求解边的长度等系列问题.
二、踏下第二步,掌握勾股定理逆定理
勾股定理的逆定理.它的意义是如果三角形中两条边的平方和等于另一边的平方,那么可证这个三角形为直角三角形.它是利用一个三角形中三条边的数学关系来证明这个图形的属性.这就为一个图形是否为直角三角形的证明问题提供了一种新的解题思路.
例2 已知△ABC的三个边分别为AB,BC,AC,三个边满足以下的数量关系:AB+BC=7,AB·BC=12,AC= 5,判断三角形的形状.
分析 由(AB+BC)2=AB2+BC2+2AB·BC=72,解得AB2+BC2=25.又因为AC2=25,所以AB2+BC2=AC2,满足勾股定理的逆定理,说明△ABC为直角三角形.
在任意三角形的模型框架中,勾股定理的逆命题可以准确地用于识别三角形的形状.同时将数学关系与几何图形有机地结合起来,为解题提供了新的思路.例2中利用代数关系的运算,结合勾股定理的逆定理的证明,判断出了三角形的形状,将逆定理学以致用.对逆命题的充分掌握同时也有利于对原命题的理解,更重要的是逆命题在解决实际问题时,有着与原命题不分伯仲的作用.
三、“用两条腿走路”,应对几何难题
实际教学中我们发现,现在考试对题目的考查更加注重对知识点的综合运用,所以勾股定理及其逆定理在解题时往往同时被使用,正所谓缺一不可.正是由于勾股定理及其逆定理构建起的代数和几何的有机关系,在解题的过程中可以综合地运用代数中的相关运算法则,为解题提供了新的思路.可见勾股定理及其逆定理在应用中是相辅相成的关系.
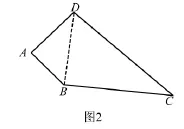
例3 在四边形 ABCD中,AB=3,AD=4,∠DAB= 90°,BC=12,CD=13,求四边形的面积.
分析 如图所示,连接DB,在Rt△ABD中,AB=3,AD=4,∠DAB=90°,根据勾股定理可得:BD2=AD2+AB2=32+42=25,DB=5.在△CBD中,DB=5,BC=12,CD=13.具有数学关系:132= 122+52,满足勾股定理的逆定理,则△CBD为直角三角形.所以Rt△ABD的面积S1为的面积S2为,四边形ABCD的面积为S+S12=36.
如上题所示的不规则图形的面积计算问题,计算的思路是将不规则图形转化为可以利用公式计算的规则图形.在辅助线的帮助下,实现了图形的转化.利用勾股定理及其逆定理将多边图形面积的计算转化为两个直角三角形的面积计算,简化了计算过程.可见在一些题目中勾股定理及其逆定理在运用中是相互促进的.
综上所述,勾股定理是一条形式简单,但内涵丰富的定理,要想充分地理解定理的实质,需要老师引导学生从定理的“正反”俩面来对定理进行透彻地理解,学会“用两条腿走路”,哪一面理解的不透彻,都会导致学习中“坡脚”现象的发生.当然在充分理解定理的基础上,更应该学会运用勾股定理及其逆定理,这需要老师引导学生增强图形转化、运算转化、数形结合的综合思考能力,做到以应用促理解,以理解化难题.可见只有“两条腿”协同作用,我们才能在应对难题中步步为营.
G632
B
1008-0333(2017)02-0052-01