狭长受限空间锚节点定位的测距仪双侧自由设站法*
刘志平,朱丹彤,杨 磊,张秋昭
(中国矿业大学环境与测绘学院,江苏徐州221116)
狭长受限空间锚节点定位的测距仪双侧自由设站法*
刘志平*,朱丹彤,杨 磊,张秋昭
(中国矿业大学环境与测绘学院,江苏徐州221116)
针对现有的狭长受限空间下锚节点定位方法的不足,在大地四边形和自由设站法基础上提出了基于测距仪的中线设站法和双侧自由设站法控制网布设方法。多余观测、待估坐标协因数阵等比较分析表明,所提出的测距仪双侧自由设站法为最优布网方法。最后,讨论了双侧自由设站法控制网图形强度优化函数及策略,并利用Leica-S910手持激光测距仪开展中国矿大室内外定位场锚节点定位试验,结果完全满足锚节点定位精度要求。
锚节点定位;双侧自由设站法;手持测距仪;狭长受限空间
狭长受限空间是一种最常见的建筑结构形式[1-3](主要有建筑走廊、交通隧道、矿井巷道等),其特点是长度尺寸远大于宽度且为封闭或半封闭空间,该类空间范围内用户位置服务是导航定位领域“最后一公里”的关键难题[4-5]。狭长受限空间的室内定位多使用由锚节点构成的无线传感器网络WSN(Wireless Sensor Networks),通过测量用户到多个锚节点的距离或信号强度等信息实现定位[6-9]。显然,确定锚节点的位置即锚节点定位,是进行高精度室内定位的前提条件。目前,现有的锚节点定位方法主要有GPS和人工配置2种方法[10-11],其中,卫星信号受遮挡等因素导致GPS法在狭长受限空间内的可用性极差;人工配置法则存在较大的人工标定误差且受限于建筑结构图保密要求。此外,如何在应急条件下有效地进行无线传感器网络构建,并快速准确地确定锚节点位置显得尤为重要[12-14]。因此,需要探讨适用于狭长受限空间的锚节点快速定位新方法。
Leica-S910手持激光测距仪别称“掌上”全站仪,测量精度为mm级、测量范围达200 m,其高精度便携式特点满足狭长受限空间的快速定位要求。一般地,锚节点多固定在狭长受限空间两侧墙体上,传统三角测量或导线测量法架站困难,而 Leica-S910因小尺寸(61 mm×32 mm×164 mm)能够较好地解决该难题。鉴此,首先探讨现有的锚节点控制网布设方法,即大地四边形法和中间自由设站法(高铁无砟轨道控制网建立方法)[15-17],在此基础上提出了改进的中间自由设站法、双侧自由设站法,进而给出了基于自由网平差和坐标转换的锚节点定位方法。其次,从控制网多余观测数、锚节点坐标参数协因数阵和控制网图形强度优化函数等方面对4种控制网方案进行比较研究。最后,利用中国矿业大学室内外定位场实测数据进行应用研究,结果验证了本文所提出的双侧自由设站法为最优布设方法。
1 狭长受限空间锚节点定位方法
1.1 锚节点控制网设计
1.1.1 现有控制网设计方案
顾及狭长受限空间自身特点和锚节点定位快速性要求,现有的能够适用于狭长受限空间的锚节点定位控制网布设方法为测距仪大地四边形法和中线自由设站法,分别记为方案1、方案2,具体布网形式如图1、图2所示。
图1为基于测距仪大地四边形的锚节点控制网。其具体要求为:直接在锚节点设站观测,相邻四边形沿走向公共一条边形成四边网,观测记录所有相邻锚节点形成的水平边长或平距值。若有已知的高等级点,应进行联测。

图1 大地四边形设站法
图2为基于测距仪中线自由设站法的锚节点控制网。该控制网采用测距后方交会原理,不同于基于边角交会原理的高速铁路无砟轨道CPⅢ控制网[15-17]和隧道洞内平面控制网[18]。具体要求为:在相邻4个锚节点的中心位置(四边形网中线位置附近)自由设置观测站,观测记录观测站至前、后视方向各三对锚节点的水平边长或平距值,自由设置站点移动策略为向前推进两对锚节点。此外,若有已知的高等级点,应进行联测。
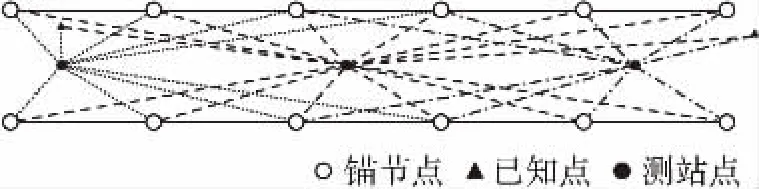
图2 中线自由设站法
1.1.2 控制网设计新方案
由于狭长受限空间内已知高等级点一般较少或缺失,上述测距仪大地四边形和中线自由设站法图形强度很弱,导致上述布网方法难以满足狭长受限空间下锚节点定位的精度要求。鉴此,下文提出基于改进中线自由设站法和双侧自由设站法的锚节点控制网方案,分别记为方案3、方案4,具体布网形式如图3、图4所示。
图3为基于改进中线自由设站法的锚节点控制网,该方法结合了大地四边形和中线自由设站法,通过增加相邻锚节点的平距观测量,企图提高图形强度。

图3 改进的中线自由设站法
图4为基于双侧自由设站法的锚节点控制网。该方法与改进的中线自由设站法基本相同,区别在于图3仅仅沿四边形网中线设置观测站,而图4采用双侧设站方式,双侧观测站同步推进且位置尽量靠近墙体或结构体。若有已知高等级点,在通视条件下应进行联测。

图4 大地四边形+双侧自由设站法
1.2 锚节点定位方法
狭长受限空间锚节点定位数据处理步骤如图5所示。首先,选择上一节介绍的方法布设并建立锚节点控制网;其次,利用Leica-S910手持测距仪进行平面边长或平距观测;再次,建立距离观测值的误差方程组,并根据自由网平差方法迭代求解待求锚节点的坐标值和方差-协方差阵;最后利用已知公共点进行坐标转换,实现室内外坐标框架统一和外符合精度评定。

图5 锚节点定位数据处理步骤
下文重点介绍图5中的锚节点定位数据处理方法。本文锚节点控制网为测距或测边自由网,须先建立距离观测值的误差方程。设两锚节点i,j坐标分别为(Xi,Yi)、(Xj,Yj),则两点之间距离的平差值^Lij可由下式表示

式中:Lij为距离观测值,vL为观测改正数为待求锚节点的坐标平差值。
对式(1)右端进行泰勒级数展开至一阶项,可得误差方程
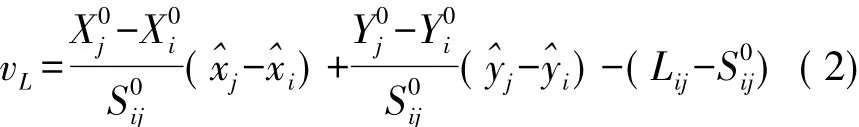
对所有水平边长或平距观测量按上述方法建立误差方程,则可形成误差方程组。一般情况下,狭长受限空间内没有已知锚节点坐标,导致控制网缺乏足够的起算基准,因此需采用秩亏自由网平差方法[19]。换言之,若误差方程组的系数矩阵记为B,则相应的法方程系数阵N=BTPB为秩亏矩阵。因此,为了获得唯一解必须引入约束基准,此时平差函数模型可表示如下
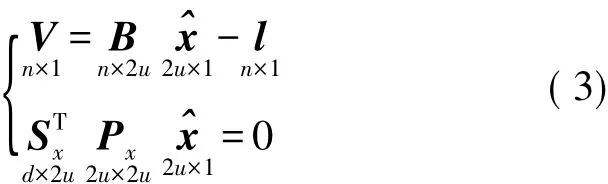
式中:n,u,d分别为距离观测的总数、待估锚节点数、附加基准数,V为距离观测值改正向量,为锚节点坐标改正向量,l为常数项,STx为附加约束条件,Px为基准权阵。
本文采用重心基准为约束条件,其相应的约束矩阵STx和基准权阵Px分别为
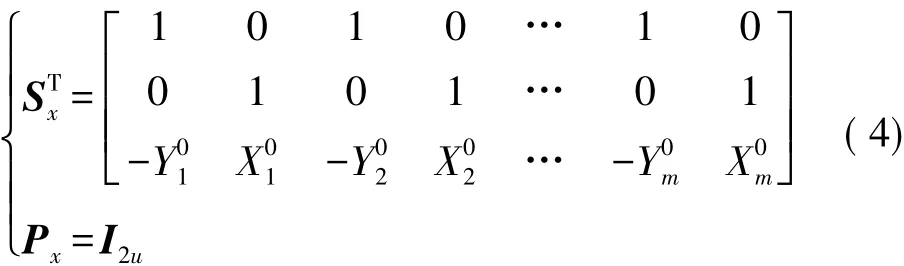
式中:I2u表示2u阶单位阵。
根据最小二乘原理VTPV+2KT(STPx)=min进行求解,可得待估锚节点的坐标改正数及其相应的协因数阵、方差-协方差阵估计式

式中:Q'=(N+PxSSTPx)-1,N=BTPB,σ0为单位权中误差,P为观测权阵,Q^x^x表示协因数阵,其大小可以反映控制网图形强度的高低。
2 应用结果及分析
2.1 控制网方案比较
为比较上述4种布网方案优劣,利用 Leica-S910在中国矿业大学室内外定位场进行实验,并通过协因数比较控制网图形强度,测试范围为中国矿业大学环境与测绘学院四楼C区走廊,走廊总长度约70 m,宽度为2.3 m,在墙体两侧布设15个锚节点,取相邻锚节点之间的横向间距为2.3 m(走廊宽度),纵向间距约为8.8 m(取值依据见2.2.1),分别使用上述4种方案设计实验(以走廊前进方向为纵向正向,横向正向与其构成右手准则,坐标系定义详见2.2.2节),按照式(5)计算各方案协因数阵,并通过比较纵横向协因数和多余观测分量确定最佳布网方案。各方案统计结果如表1所示,协因数计算结果如图6所示。

表1 控制网方案1~4统计结果
从表1可以看出,方案1~4的横向协因数均远大于纵向协因数(这与无砟铁路、隧道等情况下的协因数分布情况基本一致),故狭长型控制网应重点分析横向协因数。上述4个方案中,方案1纵横向协因数均为最大,方案2与方案3效果较为接近,但较方案1的纵横向协因数有显著减小,方案4纵横向协因数最小(纵向均值为0.22、横向均值为5.64),表明方案4通过两侧设置站点显著提高了横向的图形强度,在4个方案中效果最佳。此外,从多余观测分量也可发现,方案4的多余分量为48.7%,远远高于其他3个方案。综合考虑,建议采用方案4的布网形式。
图6显示了各锚节点的纵横向协因数,较全面比较了方案1~4的优劣,进一步验证了方案4为最佳方案。限于篇幅,不再赘述。
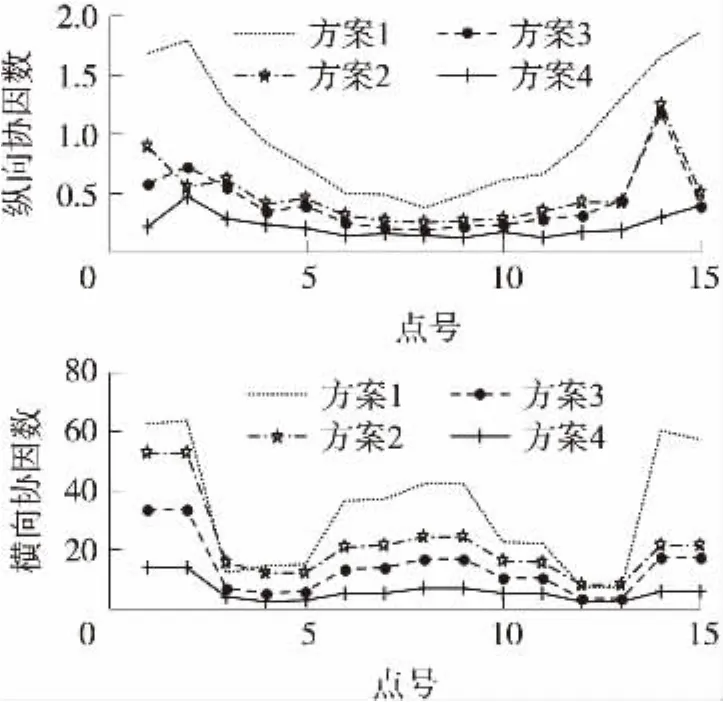
图6 方案1~4协因数计算结果
2.2 双侧自由设站法
2.2.1 控制网优化
控制网图形强度除了受不同布设方法制约,还受相邻锚节点之间的横向间距和纵向间距等影响,而横向间距一般取狭长受限空间范围的宽度。因此,为得到双侧自由设站法控制网的最佳几何图形强度,本文对协因数与横向纵向间距、锚节点个数的关系进行模拟研究。模拟方案为:(A)选定15对锚节点,变化横向、纵向间距,统计协因数的变化情况;(B)固定横向间距为2.3 m,变化纵向间距、锚节点对数,统计协因数的变化情况,模拟结果见图7所示。

图7 协因数与纵横向间距、锚节点对数的关系
图7(a)为锚节点个数固定时,协因数与横向、纵向间距的关系。模拟结果显示,纵向间距不变,横向间距在1.5 m~3.5 m范围内变化时,协因数随横向间距增加而显著减小,超过3.5 m后协因数基本趋稳;固定横向间距情况下,协因数随纵向间距的增加而缓慢增大;同时,提取最大协因数为100时的纵向和横向间距,通过拟合可近似建立控制网图形强度优化函数u=0.049w2+5.374w-1.499(w表示横向间距,u表示纵向间距),可得纵向约为横向间距5倍。图7(b)为横向间距固定时,协因数与锚节点个数、纵向间距的关系。模拟结果显示,纵向间距不变,协因数与锚节点个数近似呈正相关关系,但是在锚节点个数由奇数对增加1对变为偶数对时,协因数略微减少或不变;当固定锚节点个数时,协因数随纵向间距的变化与图7(a)相似。结合图7(a)和图7(b)可知,横向间距在1.5 m~3.5 m范围内变化时,协因数显著增大;纵向间距在整个模拟范围内,协因数增大相对缓慢;当横向间距较窄(2.3 m),锚节点对和纵向间距的增加均会导致协因数的显著增大。
综上分析可得,当横向间距可选时,应尽量宽于3.5 m;当横向间距不可选时(取狭长受限空间宽度),根据上文控制网图形强度优化函数,纵向间距应不超过横向间距的3~5倍,同时,锚节点尽量布设成偶数对。此外,对于超长的狭长受限空间锚节点控制网,可采用分组或分区平差以便削弱误差积累。
2.2.2 定位试验
为了进一步验证上述双侧自由设站法的准确性和有效性,利用Leica-S910在中国矿业大学室内外定位场进行锚节点定位试验及精度分析。测试范围为中国矿大环境与测绘学院四楼A区和C区的走廊,走廊宽度2.3 m,总长度约150 m,范围内已知高等级点3个,另布设了31个锚节点(根据3.2.1节图形强度优化函数,相邻锚节点横向间距取走廊宽度2.3 m、纵向间距约8.8 m)。设C区端点为原点,定义C区走廊前进方向为X坐标轴正向,即纵向方向,Y轴与X轴构成右手坐标系,Y轴正向记为横向方向。所建锚节点坐标系及平面分布见图8所示。
按双侧自由设站法建立锚节点控制网,并进行水平边长或平距测量(3个高等级点处均设站观测)。试验共得距离观测量228个,未知参数98个,附加基准3个,多余观测为133个,按照2.2节方法求解待锚节点坐标及中误差。结果显示,横向总体误差为7.8 cm、纵向总体误差为12.9 cm、点位总体误差为15.1 cm,能够满足定位的需求。限于篇幅,部分平差结果如表2所示。利用试验范围内的已知高等级点(最弱点点位误差约5 cm)进行坐标转换。结果显示,坐标转换误差最大值为35 cm、中误差为26 cm,不超过自由网平差总体中误差(15.1 cm)的 2倍水平,且远远高于室内定位精度要求[4](1 m~3 m),从而验证了本文方法正确性和有效性。

图8 锚节点点位分布

表2 锚节点坐标平差结果

图9 距离平差值与观测值之差
3 结论
根据平差后的坐标值可反算相邻点之间的距离,平差距离和距离观测值之差可以反映Leica-S910的测距精度,平差距离与观测值之差如图9所示。由该图可得,锚节点坐标反算的平差距离与观测距离差值最大值7.2 cm,最小值-8.4 cm,平均值1.2 cm,除个别残差较大以外,其他多数残差在±2 cm范围内随机分布,说明距离观测质量较好。需说明的是,上述统计误差远超过Leica-S910的mm级标称精度,其原因是本文顾及实际应用的快速性要求而未做精确的仪器安置和瞄准工作。
①针对狭长受限空间下锚节点定位方法的不足,探讨了狭长受限空间下4种锚节点快速测距控制网布设方法(大地四边形法、中线自由设站法、改进的中心自由设站法和所提出的双侧自由设站法),分析了各布网方法的整体精度和多余观测分量,结果表明双侧自由设站法的多余观测分量最多、精度最高。
②对协因数与横向纵向间距、锚节点个数的关系进行模拟研究,推导了锚节点控制网图形强度优化函数并提供了优化策略。中国矿业大学室内外定位场锚节点定位的测距仪双侧自由设站法结果表明,横向总体误差为7.8 cm,纵向总体误差为12.9 cm,点位总体误差为15.1 cm,完全满足锚节点定位精度要求。
[1] 王宁,秦小麟,沈尧.基于梯度的受限空间安全定位方法[J].计算机科学,2014,41(1):156-162.
[2] 张晋升,孙健,李胜广,等.狭长空间基于人体穿透损耗模型的组合定位方法[J].传感技术学报,2016,29(4):601-605.
[3] 田丰,秦涛,刘华艳,等.煤矿井下线型无线传感器网络节点定位算法[J].煤炭学报,2010,35(10):1760-1764.
[4] 刘志平,余前勇.手机传感器融合的室内三维定位试验研究[J].山东科技大学学报(自然科学版),2015,34(6):90-95.
[5] Deng Zhongliang,Yu Yanpei,Yuan Xie,et al.Situation and Development Tendency of Indoor Positioning[J].China Communications,2013,10(3):42-45.
[6] 方旺盛,高银.狭长直隧道环境中WSN的RSSI加权质心定位算法[J].传感技术学报,2014,27(2):247-251.
[7] Go S,Chong J W.Improved TOA-Based Localization Method with BS Selection Scheme for Wireless Sensor Networks[J].Etri Journal,2015,37(4):707-716.
[8] Ma D,Meng J E,Wang B,et al.Range-Free Wireless Sensor Networks Localization Based on Hop-Count Quantization[J].Telecommunication Systems,2009,50(3):1-15.
[9] Yan X,Qian H,Yu J.A Selective Beacon Node 3D Location Estimation Based on RSSI for Wireless Sensor Network[J].Information Technology Journal,2013,12(1):40-50.
[10]傅贤锋,黄亮,黄洁,等.基于超声波四元阵测距的无锚节点定位算法研究[J].仪器仪表学报,2013,34(12):2874-2880.
[11]姬靖,刘桂雄,郁文生.传感网中的四锚点节点定位实解个数分析[J].软件学报,2014(11):2627-2635.
[12]Fischer C,Gellersen H.Location and Navigation Support for Emergency Responders:A Survey[J].IEEE Pervasive Computing,2009,9(1):38-47.
[13]Ahmed A A,Al-Shaboti M,Al-Zubairi A.An Indoor Emergency Guidance Algorithm Based on Wireless Sensor Networks[C]// International Conference on Cloud Computing.2015:1-5.
[14]王群,钱焕延,戚盠,等.一种应急环境下无线传感网节点接入与定向扩散方法[J].东南大学学报(自然科学版),2014,44 (2):244-249.
[15]郝亚东,李聚方,刘利.高铁无砟轨道控制网测设和精度控制[J].测绘通报,2011(8):51-53.
[16]全志强,高占英.铁路有砟轨道CPⅢ网测量方法及精度探讨[J].测绘通报,2013(4):56-58.
[17]石德斌,王长进,李博峰.高速铁路轨道控制网测量和数据处理探讨[J].铁道工程学报,2009,26(4):26-30.
[18]周凌焱,刘成龙,高洪涛,等.高铁隧道洞内控制网测量新方法的应用[J].测绘科学技术学报,2014,31(6):570-575.
[19]崔希璋.广义测量平差[M].武汉:武汉大学出版社,2009.

刘志平(1982-),汉族,江西九江人,副教授、硕导,主要从事测量数据融合、导航位置服务、大地测量反演,zhpliu @cumt.edu.cn;zhpnliu@163.com;

朱丹彤(1993-),汉族,河南濮阳人,硕士研究生,主要从事测量数据融合处理方法与应用,18639388058@163.com。
Bilateral-Free Setting Station Method Using Hand-Held Laser Ranger for Anchor Node Positioning in Long-Narrow Confined Spaces*
LIU Zhiping*,ZHU Dantong,YANG Lei,ZHANG Qiuzhao
(School of Environment and Spatial Informatics,China University of Mining and Technology,Xuzhou Jiangsu 221116,China)
Aiming at the problem that the existed anchor node positioning methods cannot be successfully applied in the long-narrow confined spaces,this paper proposed trilateration network layout methods including both center-free station method and bilateral-free station method based on both geodetic quadrilateral method and free station method.Redundant observations and coordinates variance-covariance matrix of four trilateration network layout methods mentioned above are computed and analyzed,and results show the bilateral-free station method is the best one.Further,the structure strength function of the bilateral-free station method is investigated in detail.At the end,to test the accuracy and reliability of the bilateral-free station method,anchor node positioning experiment using Leica-S910 hand-held laser ranger is implemented in the indoor-outdoor location test field of China University of Mining Technology.The positioning results show the bilateral-free station method can get the optimized trilateration network with the position RMSE 15.1cm which can satisfy the accuracy requirement in long-narrow confined spaces.
anchor node positioning;bilateral-free station method;hand-held laser ranger;long-narrow confined spaces
10.3969/j.issn.1004-1699.2017.02.018
P25
A
1004-1699(2017)02-0272-06
无线传感器技术
项目来源:国家自然科学基金项目(41204011,41504032);大地测量与地球动力学国家重点实验室开放基金项目(SKLGED2014-3-2-E);江苏高校优势学科建设工程项目(SZBF2011-6-B35)
2016-07-27 修改日期:2016-10-31

