基于MAEKF算法的航姿参考系统设计

王丁伟，祖家奎*，黄 海

(1.南京航空航天大学自动化学院，南京210016;2.中创航空技术有限公司，浙江嘉兴314000)

基于MAEKF算法的航姿参考系统设计

王丁伟1，祖家奎1*，黄 海2

(1.南京航空航天大学自动化学院，南京210016;2.中创航空技术有限公司，浙江嘉兴314000)

构建了以低成本MEMS陀螺仪、加速度计和磁传感器组合的航姿参考系统，提出了一个乘性自适应扩展卡尔曼滤波算法。取乘性误差四元数和陀螺仪误差作为状态量，基于重力场和磁场构造了量测矢量，用于修正航姿数据。并采用准确量测法，给滤波器加入了四元数的归一化约束，最后给出了基于新息的估计量测噪声方差矩阵的公式。通过仿真和试飞验证，表明本文设计的低成本的航姿参考系统能够提供比较准确的航姿信息。与常规的扩展卡尔曼滤波器比较，本文设计的乘性自适应扩展卡尔曼滤波算法有效提高了系统的精度和稳定性，并且具有较好的鲁棒性。

航姿参考;乘性扩展卡尔曼滤波;自适应;误差四元数

航姿参考系统能够准确测量载体的空间姿态信息。在三维空间中，通常采用俯仰角、滚转角、航向角来描述其姿态信息。在军事、航空航天、航海等领域多采用高精度的惯性测量元件，但其价格昂贵。随着价格低廉的MEMS惯性传感器的发展，低成本的航姿参考系统广泛应用于消费类的无人机、室内导航、智能穿戴设备、游戏手柄等领域。低成本的航姿参考系统一般由MEMS陀螺仪、加速度计、磁传感器组成［1］。但是，MEMS陀螺仪存在严重的零点漂移、随机误差，直接对原始数据进行积分得到的角度会产生很大的累积误差，并且该误差会随着时间不断增大［2］。因此，辅以加速度计和磁传感器测量的重力场、地磁场来补偿MEMS陀螺仪的误差能够显著提高航姿数据精度［3］。

目前广泛采用的航姿融合算法主要分为互补滤波、扩展卡尔曼滤波两大类。从融合效果看，互补滤波的精度不高，且动态响应速度不如卡尔曼滤波迅速［4］。文献［1，5］分别提出各自的互补滤波算法，前者采用PI调节器，先使用加速度计数据补偿陀螺仪数据，然后再融合磁场数据;后者采用向量叉乘解算陀螺仪误差，并且能够直接运用于未校准的传感器，能够获取相对较好的姿态数据。但是两者的融合精度都不是很好。文献［4，6］设计了基于四元数的扩展卡尔曼滤波器，前者着重介绍了使用MPU9250作为MEMS九轴姿态传感器，实现EKF算法;后者先用重力场补偿陀螺仪误差，再用磁场修正偏航角，接着构造了自适应的量测噪声方差矩阵，但是其本质仍然还是加性扩展卡尔曼滤波器，脱离了四元数归一化的约束，滤波器极易发散。而乘性扩展卡尔曼滤波器能够较好的保持四元数的归一化约束，文献［2，7］以乘性误差四元数作为状态量，设计了乘性扩展卡尔曼滤波器。其中，文献［2］仅仅采用磁场信息修正陀螺仪误差，这样的确避免了振动和载体运动导致的干扰，但是，磁力计易受到外部磁场干扰，导致姿态数据错误;文献［7－8］则是加入了加速度计，但是并未给出如何设计量测噪声方差矩阵。

针对上述众多问题，本文设计了一种可靠的航姿参考系统，该系统采用MAEKF算法进行航姿融合，适用于量测噪声多变的复杂环境，并且通过仿真和试飞测试验证了该航姿参考系统的可靠性。

1 系统结构

本文将MEMS陀螺仪、加速度计、磁传感器的数据作为MAEKF的输入。其中，加速度计的原始数据需要经过低通滤波器滤除高频噪声和震动干扰。本文设计的航姿参考系统结构和实物图，如图1所示。

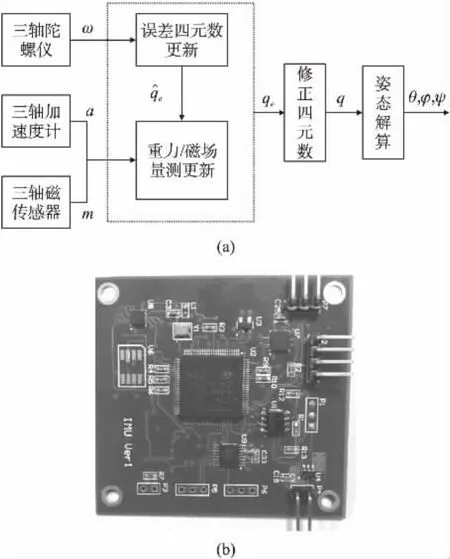
图1 航姿参考系统结构图和实物图

三轴陀螺仪数据驱动误差四元数的更新，通过加速度计和磁传感器所测得的重力场和磁场来修正，从而得到误差四元数的最优估计。用该误差四元数修正陀螺仪数据积分的四元数，再通过姿态解算，得到精度较高的姿态角数据。该系统采用MPU6050和HMC5803作为姿态传感器，STM32F429作为核心处理器。

2 航姿融合算法设计

2.1 乘性误差四元数

姿态解算算法中，有多种参数化方法，比如欧拉角、四元数、改进的Rodrigues参数、等效旋转矢量等［9］。由于四元数的非奇异性、计算量小等优点，使其广泛应用于姿态解算算法中。四元数必须满足归一化约束，然而标准EKF方法释放了四元数的归一化约束。为了克服这种缺陷，本文采用乘性误差四元数方法。

对式(1)两边求微分得到:

由四元数运动学方程可得:

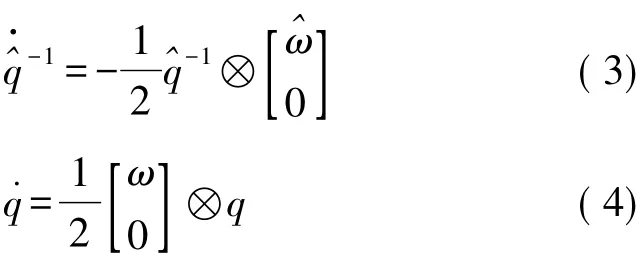
综上可得误差四元数运动学方程:

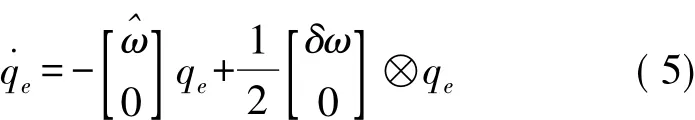
2.2 系统状态方程设计

2.2.1 MEMS陀螺仪建模

系统状态方程主要描述了陀螺仪输出的角速率值和误差四元数之间的动力学关系。因此，设计状态方程之前，首先要完成MEMS陀螺仪的建模。

陀螺仪的误差主要来源于随机漂移和噪声，一种广泛采用的数学模型是一阶马尔可夫过程，其主要形式如下:

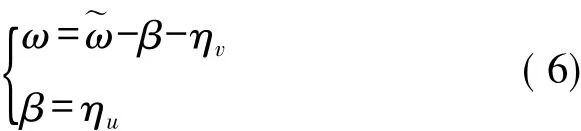
式中:ηv和 ηu分别表示具有谱密度σ2vI3×3和 σ2uI3×3的零均值高斯白噪声过程;β为偏置向量;珟ω为测量观测值［9］。

估计的角速度为

2.2.2 建立状态方程

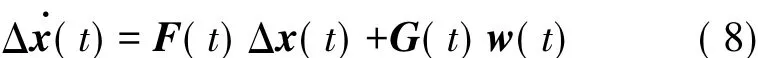
式中:

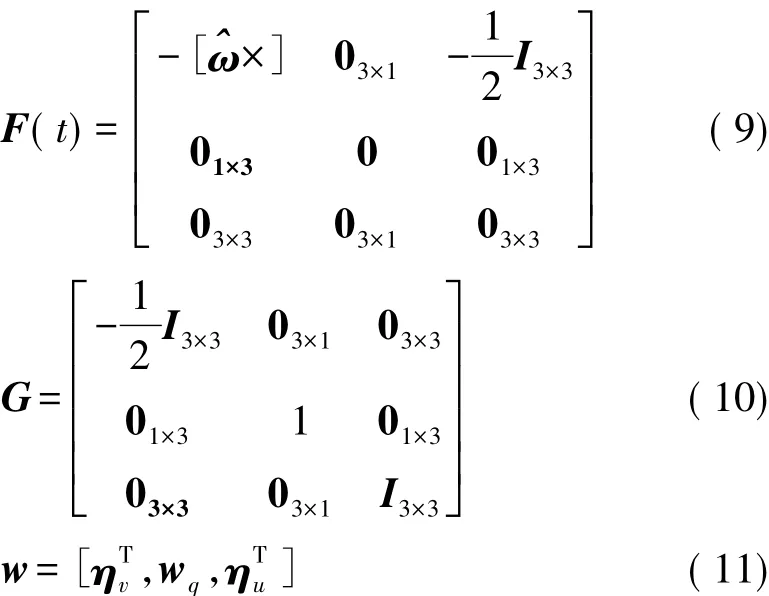
2.3 量测方程设计

2.3.1 姿态误差的测量

EKF中的量测方程能够起到修正状态预测值的作用，在许多关于AHRS的研究中，状态方程的建立大多不尽相同，主要区别在于量测方程的量测量的选取中。本文选用符号p和m表示状态量的预测值和量测值，e表示预测值和量测值的外积，θe表示两个向量的内积，则

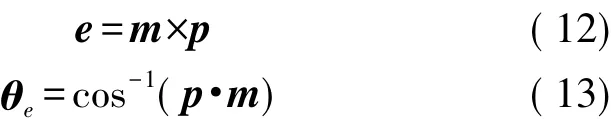
式中:向量p和m均为单位向量。

通过式(12)、式(13)构建姿态误差向量:

乘性误差四元数与姿态误差向量之间的关系为［7］:

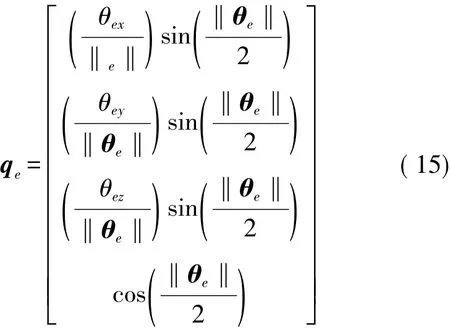
本文选用了加速度计和磁传感器作为量测的传感器。接下来，分别对两个传感器设计量测方程。

2.3.2 加速度计的量测设计

加速度计的输出主要包含重力加速度、运动加速度以及噪声，可用如下形式表达:

式中:am表示加速度计输出，Cbng表示重力向量在机体轴下的投影，表示运动加速度，b表示加速度计的噪声。

通过重力加速度在机体轴下的分量可以计算出，当前载体的滚转角和俯仰角。因此，当载体的运动加速度较小时，式(16)可以近似为:

式中:gb表示重力加速度在机体轴下的投影。

显然，gb=Cbng是成立的。其中:

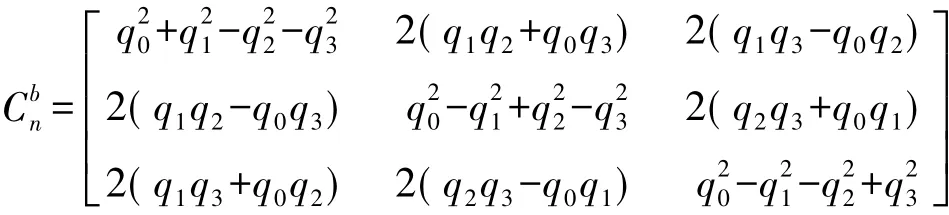
由式(12)、式(13)得:

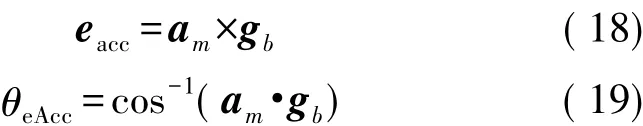
式中:am需要归一化处理。

2.3.3 磁传感器的量测设计

磁传感器测量的是三轴的磁场强度，其输出形式如下:

式中:mm表示磁传感器的输出，m0表示当地的地磁强度，b表示磁传感器的噪声。

同理，由式(12)、式(13)得:

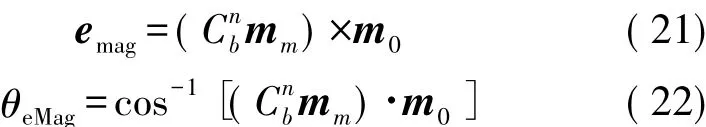
2.3.4 准确量测法的状态约束

由于乘性误差四元数是严格归一化的。因此，在滤波过程中，必须满足归一化约束才能有效的防止滤波器的发散［10］。其归一化方程为:

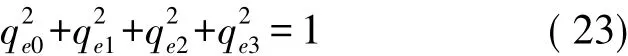
将式(23)作为状态量的伪量测方程，引入到系统的量测中，构成系统的量测方程。

2.3.5 建立量测方程

由式(15)、式(23)可知，量测方程中包含有量测量和状态约束两个部分。系统的量测方程为:

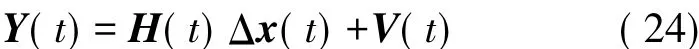
式中:

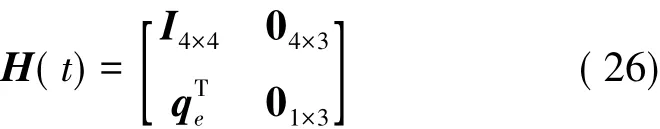
2.4MEKF算法

基于MEKF的姿态融合算法区别于AEKF(加性扩展卡尔曼滤波)的地方在于:AEKF直接选用姿态四元数作为滤波器的状态量，姿态误差采用加性修正，这种加性修正很容易破坏姿态四元数的归一化约束，降低滤波精度，更严重可能导致滤波器发散［9，12－13］。而MEKF虽然在形式上比AEKF复杂一点，但是，却能够很好的保持姿态四元数的归一化约束。

状态四元数传播方程:

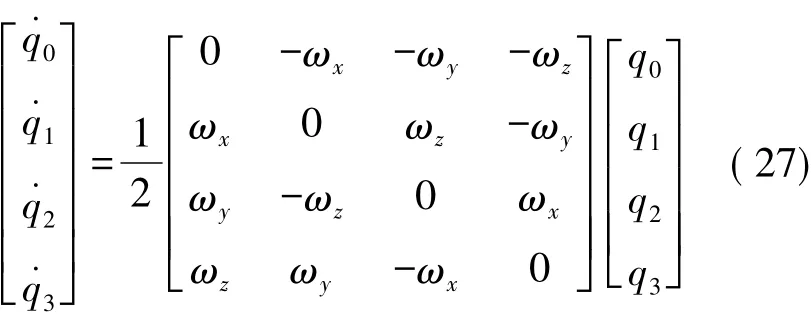
状态预测方程:

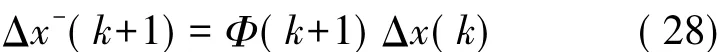
协方差预测方程:

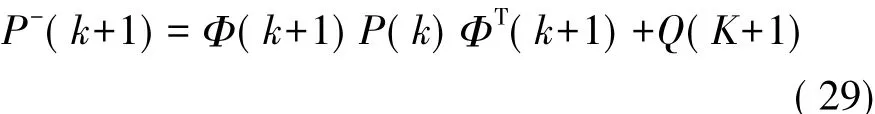
卡尔曼增益方程:

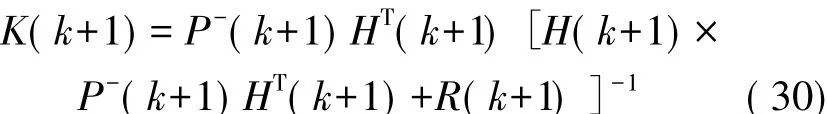
信息方程:

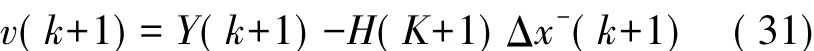
状态更新:

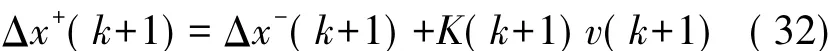
协方差更新方程:

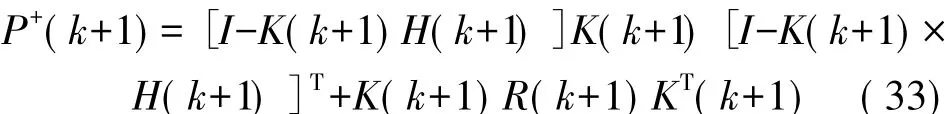
状态量归一化:

姿态四元数修正:

姿态四元数归一化

注意:MEKF迭代过程中，每次姿态四元数修正结束后，误差四元数需要重置为初始值。

3 航姿融合算法实现

本文构建了两组量测向量，Murrell对这种滤波器进行了改进［9］。该算法每次迭代过程仅需要处理一组3×1的量测向量。对于本文中设计的算法，一次完整的修正过程需要连续处理两组量测向量。

从图2可以看出，当系统中设计了n个量测向量，该算法采用序贯方式一个一个处理量测向量。这样处理的优点在于:降低了量测方程的维度，在进行增益解算时，矩阵逆的计算复杂度大大降低，能够有效提高算法实时性。另外，由于不同传感器的采样频率不同，因此这种序贯处理方式使得只有传感器采样到新值时才进行量测更新，避免了旧值的重复计算。

4 自适应量测噪声R阵设计

卡尔曼滤波器的公式中主要有两个噪声矩阵，分别是系统噪声矩阵Q和量测噪声矩阵R。就系统噪声而言，其决定于系统内部机理，噪声参数相对稳定，可以通过大量实验来实现精确测试或建模;但是量测噪声不仅仅来源于MEMS传感器的误差和噪声，还受到外部环境以及载体运动状态等情况影响［14］。因此量测噪声是比较容易变化的，有太多的不确定性，难以建模。因此，需要算法对量测噪声进行实时的自适应估计，这样才能保证滤波器的精度，防止滤波器发散。

Sage-Husa自适应扩展卡尔曼滤波算法(SHAEKF)在理论上实现了在进行状态估计的同时还可在线自适应估计系统噪声和量测噪声统计特性的功能。其Q、R阵的自适应算法如下:

在实际运用中，SHAEKF算法所估计出来的系统噪声和量测噪声方差序列分别与真实噪声方差存在差值误差，特别是系统噪声的估计偏离更大，极易导致对量测值的权重过高，等效于状态方程失效，大大降低了滤波精度，甚至会导致滤波器发散［14］。

本文采用改进型的SHAEKF算法估计R阵，其公式如下:

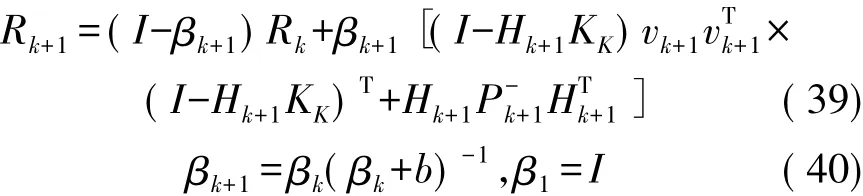
式中:b为渐消因子，一般取b=0.9～0.999。

5 仿真与试飞验证

5.1 仿真条件

本文使用MATLAB对MIMU的源数据进行处理。MIMU传感器由MPU6050和HMC5803组合而成，处理器选用了意法半导体(ST)公司Cortex－M4架构的STM32F429(图1)。设置MPU6050采样频率500 Hz，HMC5803为75 Hz，数据上传频率为100 Hz。因此，在MATLAB下仿真时，算法解算周期为0.01 s。

5.2 仿真结果

根据上述条件，对MIMU静置1 h，在MATLAB下对采集到的数据进行了MAEKF算法和传统EKF算法的姿态解算，取中间50 s数据，如图3和图4所示。

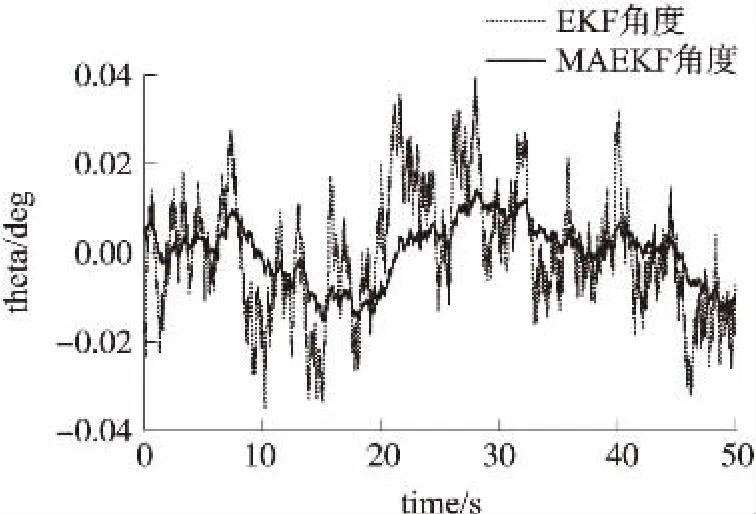
图3 俯仰角静态图

图中，横轴为时间轴，单位是s，纵轴表示航姿数据，单位是(°)。从图中可以看出，本文设计的MAEKF算法的静态精度比传统的EKF算法精度要高。MAEKF算法的俯仰角和滚转角静态精度分别达到了0.016°和0.013°。

仿真中，对量测噪声方差矩阵R取了二范数，根据本文的自适应算法，其曲线如图5所示。图5中R阵初始值给的是单位矩阵，最终，其二范数收敛至0.166 7。

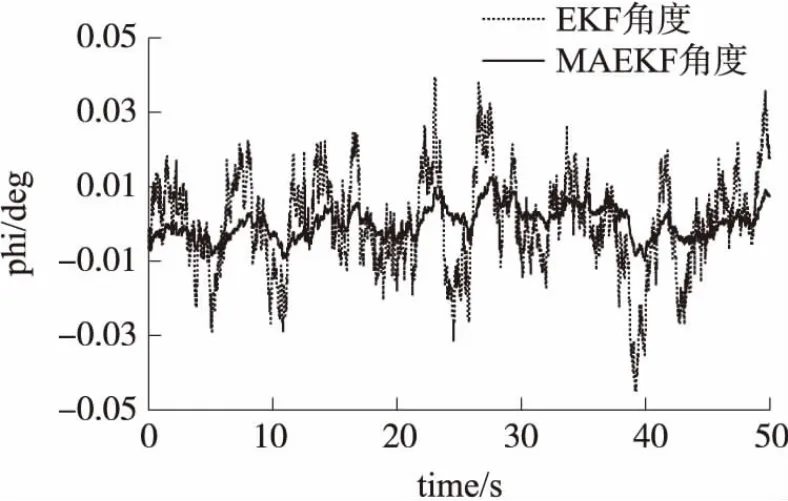
图4 滚转角静态图

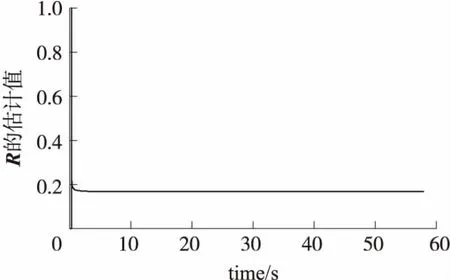
图5 R阵估计结果图

5.3 试飞验证与分析

试飞验证的飞行器为一个三轴六桨飞行器，如图6所示。该飞行器搭载有本文设计的AHRS传感器，该传感器中同时运行了标准扩展卡尔曼滤波算法(EKF)和本文设计的乘性自适应扩展卡尔曼滤波算法(MAEKF)，通过uCOS－Ⅱ来调度，算法解算频率均为100 Hz。另外，飞行器上还搭载了一款参考IMU，型号为IMU520，能够提供精确的滚转角和俯仰角。

图6 飞行器实物图

如图7、图8给出参考IMU的输出、EKF算法的输出、文中设计的MAEKF算法的输出曲线。

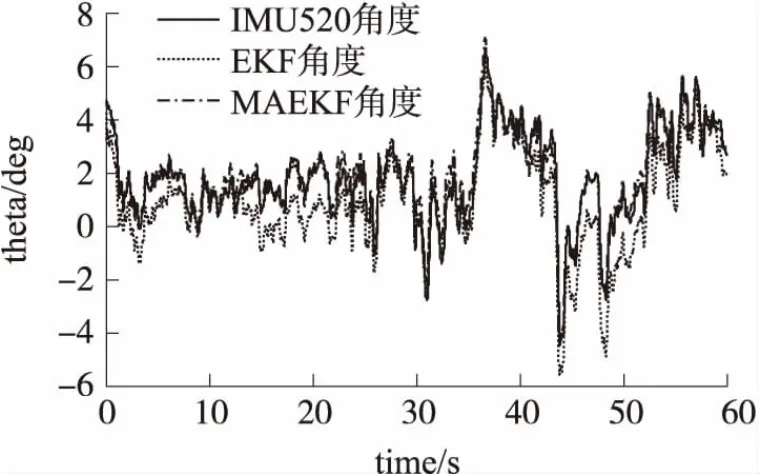
图7 试飞俯仰角曲线图

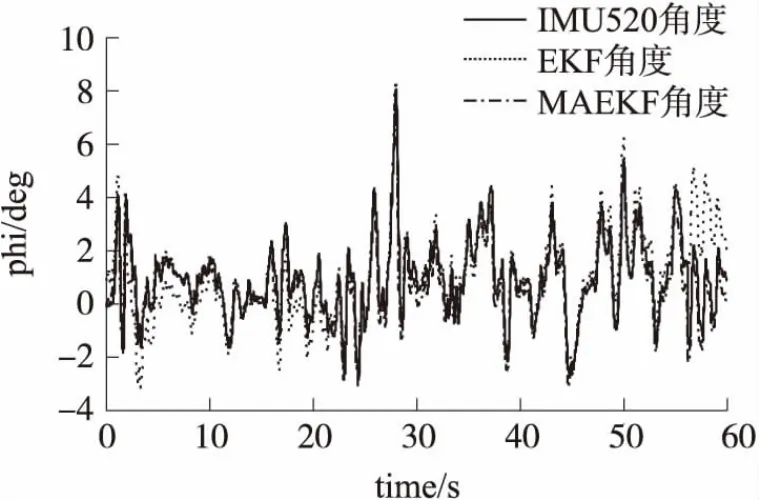
图8 试飞滚转角曲线图

图9给出了两种算法的误差对比曲线图。本文设计的航姿融合算法一般的扩展卡尔曼滤波算法精度要高很多，能够较好的适应不确定的量测噪声。

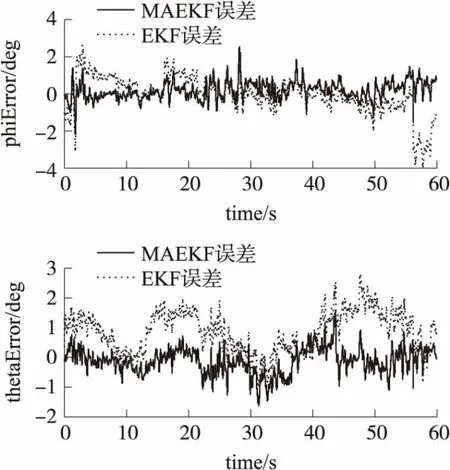
图9 MAEKF与EKF误差比较曲线

表1中统计了两种算法角度误差的最大值、平均值和标准差。与EKF算法相比，MAEKF算法产生的最大误差和标准差更小，较小的最大误差说明了该算法的具有更好的精度，而较小的标准差则说明了在具有量测扰动的情况下，该算法更加稳定，具有更好的鲁棒性。

图10给出了飞行过程中，飞行器机体轴3个轴向的加速度信息。可以看出，飞行过程中有无刷电机导致的高频振动。常规的EKF算法直接采用姿态四元数作为状态量，且采用常值R阵，不能适应噪声多变的飞行环境;而本文设计的MAEKF算法，采用自适应R阵，根据新息估计量测噪声的方差，同时，采用了直接观测法引入了四元数的归一化约束，提高了航姿融合算法的滤波精度和鲁棒性。

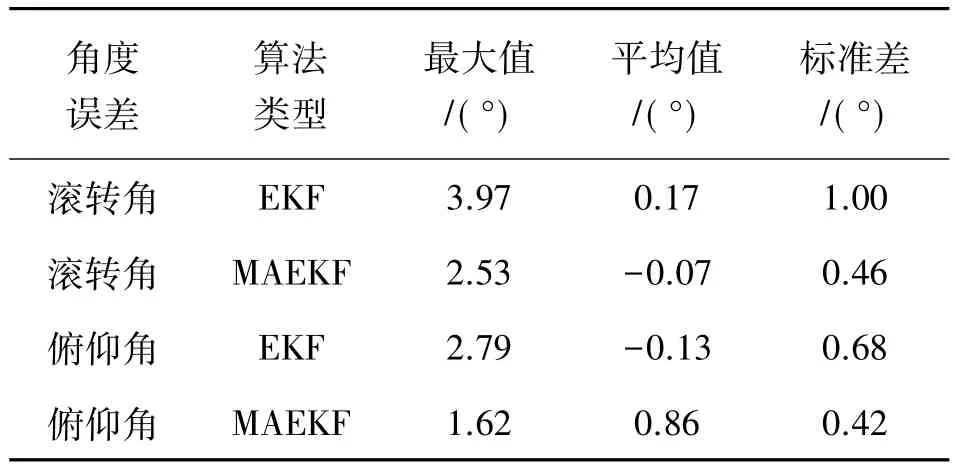
表1 EKF和MAEKF比较

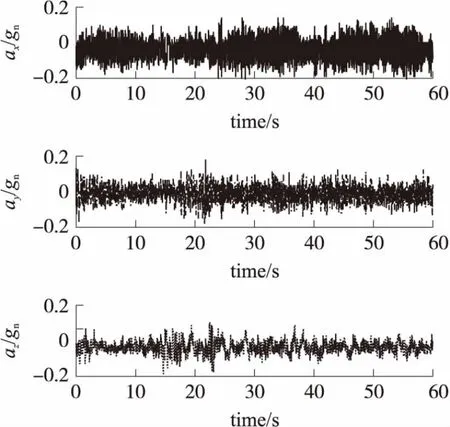
图10 试飞加速度曲线图

6 结论

本文从实际应用角度出发，设计了一个低成本航姿参考系统。其中包括MAEKF算法，该算法通过采用约束滤波和自适应的量测噪声矩阵，与常规的EKF算法比较，仿真与试飞验证的结果表明，MAEKF算法不仅有更高的精度，而且对不确定的量测噪声具有更好的鲁棒性。在航姿参考应用领域具有很好的应用前景。

［1］ 杜彬彬，吴昊，张继文，等.一种面向AHRS的改进互补滤波融合算法［J］.国外电子测量技术，2015，34(3):13－18.

［2］ 薛亮，李天志，李晓莹，等.基于MEMS传感器的微型姿态确定系统研究［J］.传感技术学报，2008，21(3):457－460.

［3］ 赵代弟.MARG姿态测量系统抗干扰算法研究［D］.2015.

［4］ 刘春阳，徐军领，程洪涛，等.MPU9250传感器的姿态检测与数据融合［J］.河南科技大学学报，2015，36(4):14－17.

［5］ Hamel T，Mahony R.Attitude Estimation on SO(3)Based onDirect Inertial Measurements［J］.IEEE International Conference on Robotics and Automation，2006:2170－2175.

［6］ 刘兴川，张盛，李丽哲，等.基于四元数的MARG传感器姿态测量算法［J］.清华大学学报，2012，52(5):627－631.

［7］ Mohammad A，Alireza K，Paknush K.Orientation Estimation by Error-State Extended Kalman Filter in Quaternion vector space［J］.SICE，2007 Annual Conference，2007:60－67.

［8］ 叶锃锋，冯恩信.基于四元数和卡尔曼滤波的两轮姿态稳定方法［J］.传感技术学报，2012，25(4):524－528.

［9］ John L Crassidis，John L Junkins.动态系统最优估计［M］.2版.北京:国防工业出版社，2016，1:357－365.

［10］薛亮，姜澄宇，常洪龙，等.基于状态约束的MIMU/磁强计组合姿态估计滤波算法［J］.中国惯性技术学报，2009，17(3): 338－343.

［11］ James K Hall，Nathan B Knoebel，Timothy W McLain.Quaternion Attitude Estimation for Miniature Air Vehicles Using a Multiplicative Extended Kalman Filter［J］.IEEE Position，Location and Navigation Symposium，2008:1230－1237.

［12］李翔.基于MARG传感器的AHRS关键技术研究［D］.2013.

［13］李建国，催祜涛，田阳，等.基于乘性四元数和约束滤波的飞行器姿态估计算法［J］.系统工程与电子技术，2013，35(5): 1031－1036.

［14］张欣.多旋翼无人机的姿态与导航信息融合算法研究［D］.2015.

王丁伟(1991－)，男，江苏扬州人，硕士研究生，主要研究方向为无人机飞行控制，812724408@qq.com;

祖家奎(1974)，男，江苏徐州人，副研究员，主要从事无人直升机飞行控制技术、多变量控制技术及其应用、系统仿真与建模技术、嵌入式系统开发等方向，zujiakui@nuaa.edu.cn。

The Design of AHRS Based on MAEKF

WANG Dingwei1，ZU Jiakui1*，HUANG Hai2
(1.College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China; 2.ZhongChuang Aviation Technology Co.Ltd，Jiaxing Zhejiang 314000，China)

An attitude and heading reference system(AHRS)is designed which is composed of low cost MEMS gyroscopes，accelerometers and magnetometer and a multiplicative adaptive extended kalman filter algorithm(MAEKF)is proposed based on the gravity field and magnetic field constructed measurement vector.In order to correct attitude and heading data，the MAEKF algorithm selects quaternion error and bias of gyroscopes as state vector.Then，the accurate measurement method is adopted to provide the filterwith normalized constraint.Furthermore，this paper presents an innovation-based formula which is used to estimate measurement noise covariance matrix.Finally，simulation and flight-test show that the designed AHRS can provide accurate attitude and heading data.Compared with traditional extended kalman filter(EKF)，the MAEKF algorithm effectively improves the accuracy，stability and robustness of the system.

attitude and heading reference system;multiplicative extended kalman filter;adaptive;quaternion error EEACC:2575;7230;7630 doi:10.3969/j.issn.1004－1699.2017.02.026

10.3969/j.issn.1004－1699.2017.02.026

TJ765

A

1004－1699(2017)02－0319－07

2016－08－03 修改日期:2016－09－22