一个电磁感应问题的研究

林佩珠

(广东第二师范学院物理与信息工程系，广东 广州 510303)

一个电磁感应问题的研究

林佩珠

(广东第二师范学院物理与信息工程系，广东 广州 510303)

本文用Mathematica-10.3对磁场中一个典型的落棒运动问题进行深入研究,先计算加速度、电流和着地时间对金属棒电阻的依赖关系, 澄清现有文献中一处混乱说法. 接着讨论该电路中能量的转化问题. 最后研究导轨电阻对金属棒运动规律的影响. 数值结果表明:由于棒的下落距离不长,轨电阻对金属棒运动规律的影响很小.

磁场; 落棒运动; 电磁感应

1 引言

磁场对载流导体的作用和电磁感应的综合问题,是大学电磁学[1]以及高中电磁学教学中一个重要内容.为了回避复杂的数学,常常把问题理想化:同时忽略回路的所有电阻和摩擦力.然而,过于简单化有时会掩盖了物理实质,容易得出错误的论断.下面问题就是一个有代表性的实例.[2]

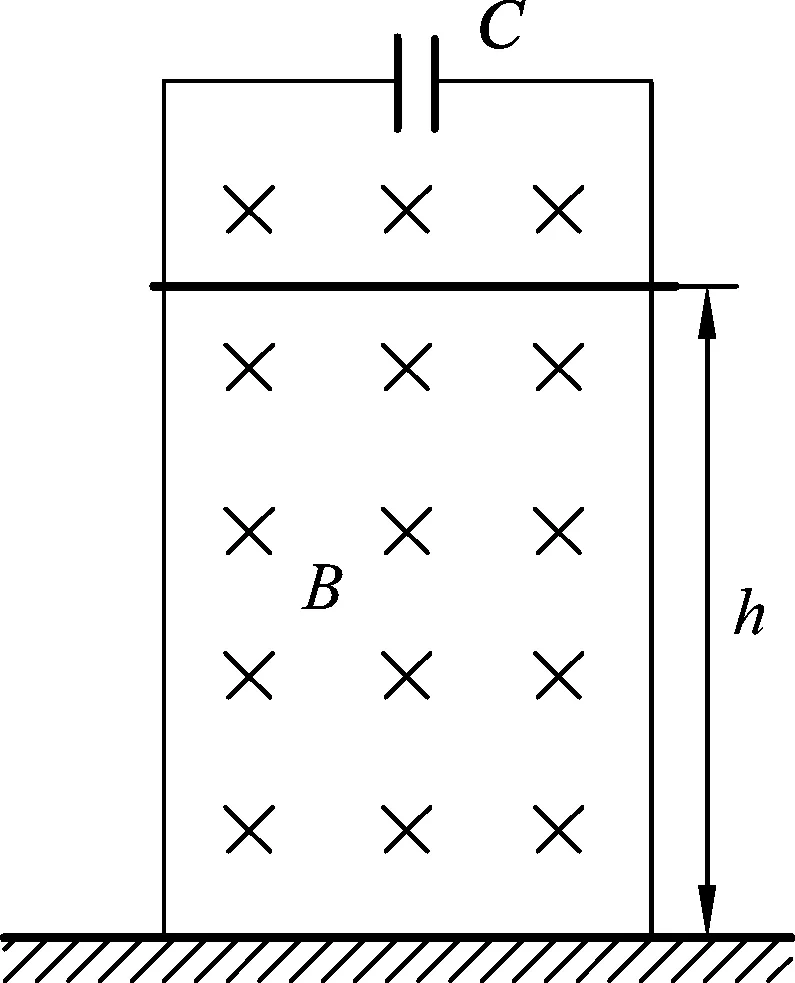
图1 磁场中的金属棒

如图1所示,两根竖直地放置在绝缘地面上的金属框架.框架的上端接在电容为C的电容器上.框架上有一质量为m, 长为l的金属棒,平行于地面放置,与框架接触良好无摩擦,棒离地面的高度为h.强度为B的匀强磁场与框架平面相垂直,开始时电容器不带电.自静止起将棒释放,问棒落到地面需多长时间?

这是参考文献[2](其题目为《电学中的几件“怪事”》,以下简称文[2])中提出的第五件“怪事”,并冠以副标题“粗看似是变加速,细算却是匀加速”、给出了如下解法.

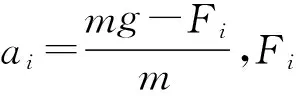
ΔU=BlΔv,ΔQ=CBlaΔt,i=CBla,F=CB2l2a.

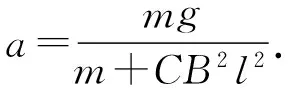
但是,文献[2]的以上解法过于简单化,掩盖了物理实质,漏掉了重要的物理过程;所得出的论断“粗看似是变加速,细算却是匀加速”是不符合实际的.

本文将对这个问题进行深入的研究,分析造成这件“怪事”的原因.

2 一种简化的动力学分析

在文献[2]所提供的上述解法中,既不计摩擦力,又忽略了回路的电阻,这本身就是一对矛盾,在实际中是难以兼顾的.为了使金属棒与框架摩擦力可以忽略,棒与框架就不能“夹”得太紧,那么棒与框架的电接触就不可能如此良好,以致于一点接触电阻也没有.

本问题的核心是回路电阻对电磁感应进程快慢的影响,而摩擦力的主要作用是抵消一部分重力(从而相当于减少了重力加速度,例如把g=9.81m/s2减少为g*=9.75m/s2),所以比较为接近实际的简单处理方法是:忽略摩擦力和框架(导轨)的电阻,考虑棒和框架的接触电阻及棒本身的电阻, 记总电阻为R.当然,这样处理会使问题就变得复杂一点,其解答需要求解微分方程,并作具体的数值分析,但这样将有助于还原物理过程,弄清棒的加速度和电流的变化情况,从而弄清楚出现“怪事”的原因.

2.1 动力学微分方程的解

设在t时刻,棒的速度为v, 电动势为E;电流为i,电容器的电荷量为q,电压为u,则由

可得

(1)

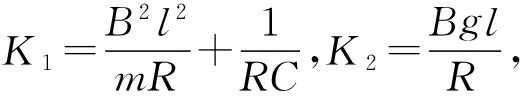
(2)

这是一阶常系数微分方程,利用原题目所给定的初始条件:当t=0时,v=0，即E=0,i=0,容易求得其解为

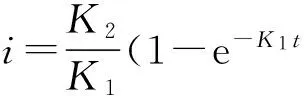
(3)

(4)

即棒的加速度a随时间t的增加作指数下降.

对(4)式积分, 可求得速度v和下降高度x随时间t的变化规律

(5)

(6)

2.2 运动规律数值分析

从(4)式易得:当t=0时,a0=g,这是因为棒刚刚释放时,v=0,棒没有切割磁感线,没有安培力.若引入电路时间常数

(7)

则当t≫τ时,e-K1t→0,(4)式变为文献[2]的结果:

(8)

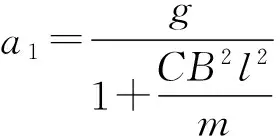
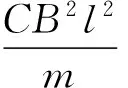
有了以上参数,并取h=1.2 m和g=9.8m/s2,利用(3)～(6)式,就可以根据不同R值具体讨论金属棒的加速度a、速度v和下降高度x随时间t变化的规律,以及棒落到地面所需的时间.

虽然高度x随时间t变化的规律已经由(6)式给出,但计算金属棒落地时间仍然比较复杂,需要有效的数值计算,使用Mathematica的找根命令FindRoot可以高精度地求得满足x(t)=h的tm落地时间. 表1给出了不同电阻对应的落地时间tm和5倍时间常数.

表1 4种电阻对应的落地时间tm和5倍时间常数(取g=9.8m/s2,h=1.2m)

图2给出了4种电阻对应的0～0.5s内加速度a随时间t变化的规律;图3和图4分别给出了0～0.5s内速度v和金属棒下降高度x随时间t变化的规律.

图2 对应于4种电阻,前0.5s内

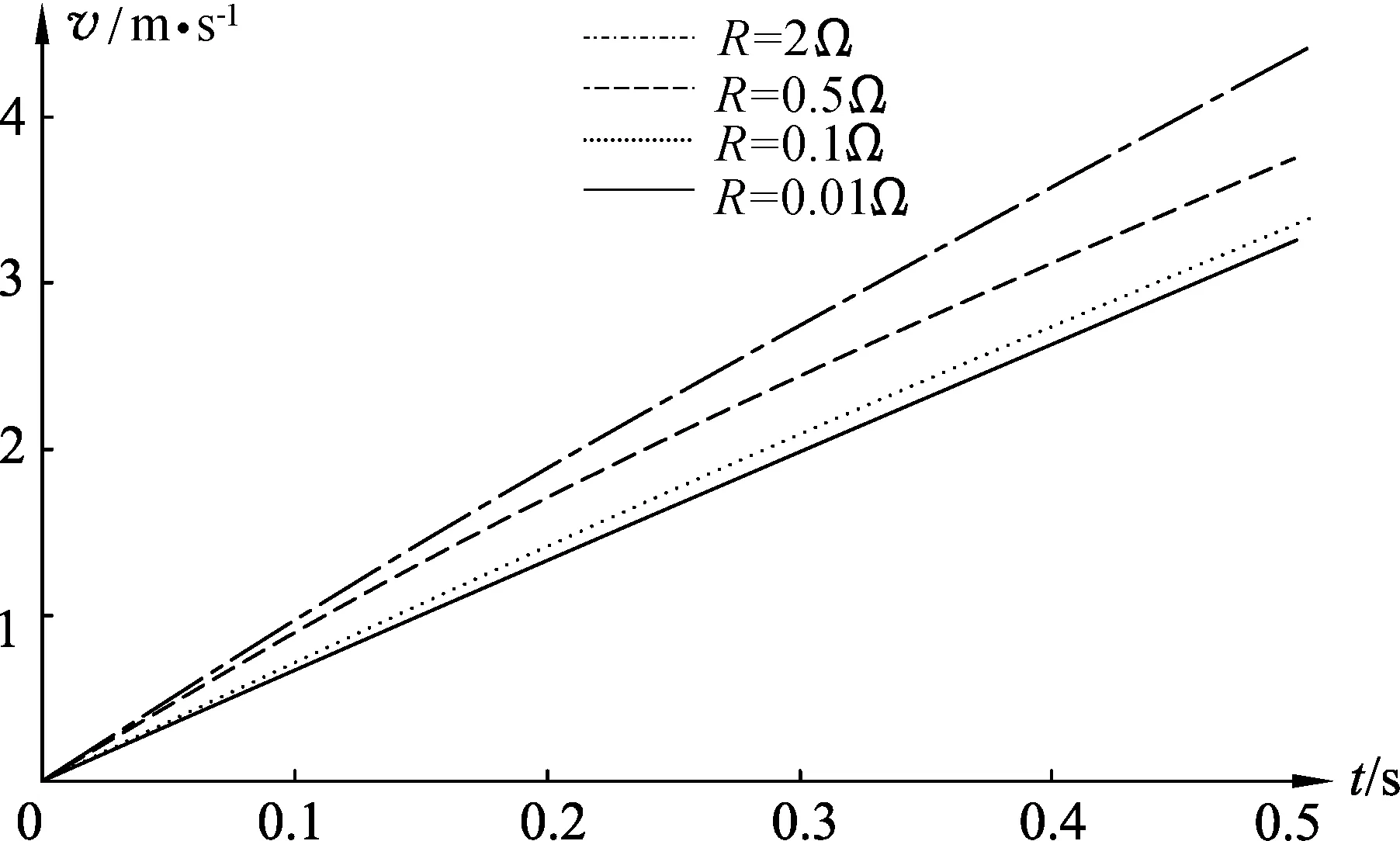
图3 对应于4种电阻,前0.5s

图4 对应于4种电阻,前0.5s内

从表1和图2可见:由于实际的电路存在着电阻(接触电阻和金属棒的电阻),金属棒下落过程不是匀加速运动而是变加速运动.当R=0.5Ω时,棒从释放到落地的全过程都做变加速运动;即使电阻较小,金属棒下落的初期也是变加速运动,例如当R=0.1Ω时,前面28.2214%的时间内都是变加速运动.

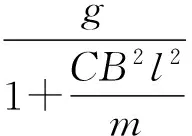
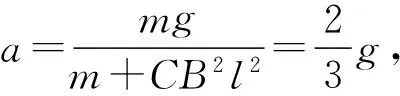
2.3 电阻消耗的热能、能量的转换与守恒

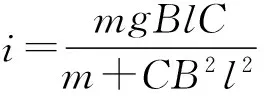
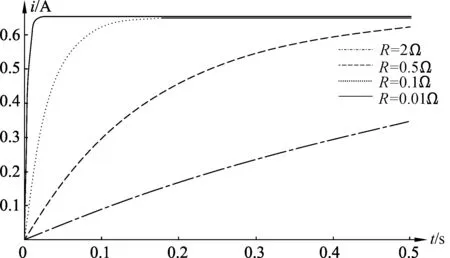
图5 对应于4种电阻,前0.5s内

回路电流的第1个效应就是在电阻上产生焦耳热,可通过下式计算

电流的第2个效应是给电容器充电,t时刻的储能为

与此同时,金属棒动能不断增加

(11)

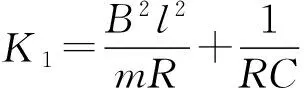
Q+EC+T=

(12)

容易验证,式(12)正好等于势能减少量mgx(t),这说明在金属棒下落过程中每时每刻保持着能量守恒,重力对金属棒所做的功(即势能减少量)一部分用于电阻发热、一部分用于给电容器充电储能、一部分用于动能的增加.

图6当R=0.5 Ω时, 前0.5s内各能量随时间t的变化规律.

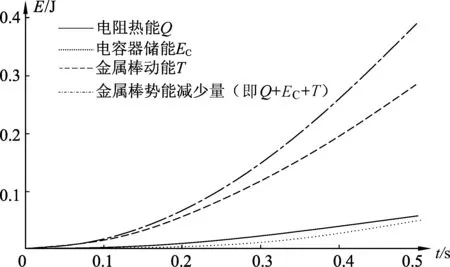
图6 当R=0.5 Ω时, 前0.5s内

3 导轨电阻对金属棒运动规律的影响

导轨电阻随着棒的下落线性增加(回路导线长度线性增长),用R0表示接触电阻和t=0时刻回路的总电阻,导轨每2m(双轨)的电阻为κ,则t时刻回路总电阻为R=R0+κ·x(t),这时动力学方程必须转换为x(t)的微分方程. 由

u=Blv-iR，

得

(13)

这是变系数三阶微分方程,没有解析解,可使用Mathematica系统的标准数值解法,[3]其初始条件为x(0)=0，x′(0)=0和x″(0)=g. 当κ=0时, (13)式回到不计导轨电阻的情况.

铜的电阻率为0.017 Ω/(m/mm2),考虑到导轨(双轨)长度为2x(t),如取导线的横截面为6.8mm2,则κ=0.005Ω/m.当R0=1Ω时,取κ=0.005Ω/m和κ=0,加速度随时间t的变化规律如图7所示;当R0=0.1Ω时,取κ=0.005Ω/m和κ=0,加速度随时间t的变化规律如图8所示. 为了检验数值解法的可靠性,图7和图8也给出了κ=0对应的解析解.

由图7和图8以及更详细的计算(不同R0对应的数值结果,限于篇幅未给出)可得出如下结论:

(1)κ=0的数值解(点线)与κ=0的解析解(实线)完全一致,这说明本文的数值解法是准确可靠的.

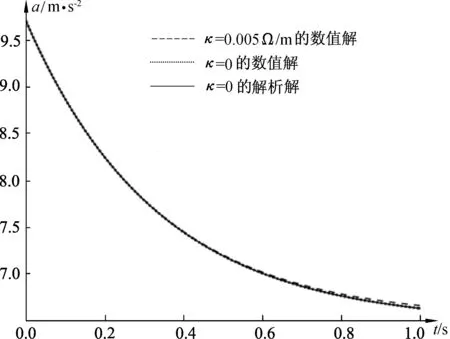
图7 当R0=1Ω时导轨电阻对金属棒加速度的影响

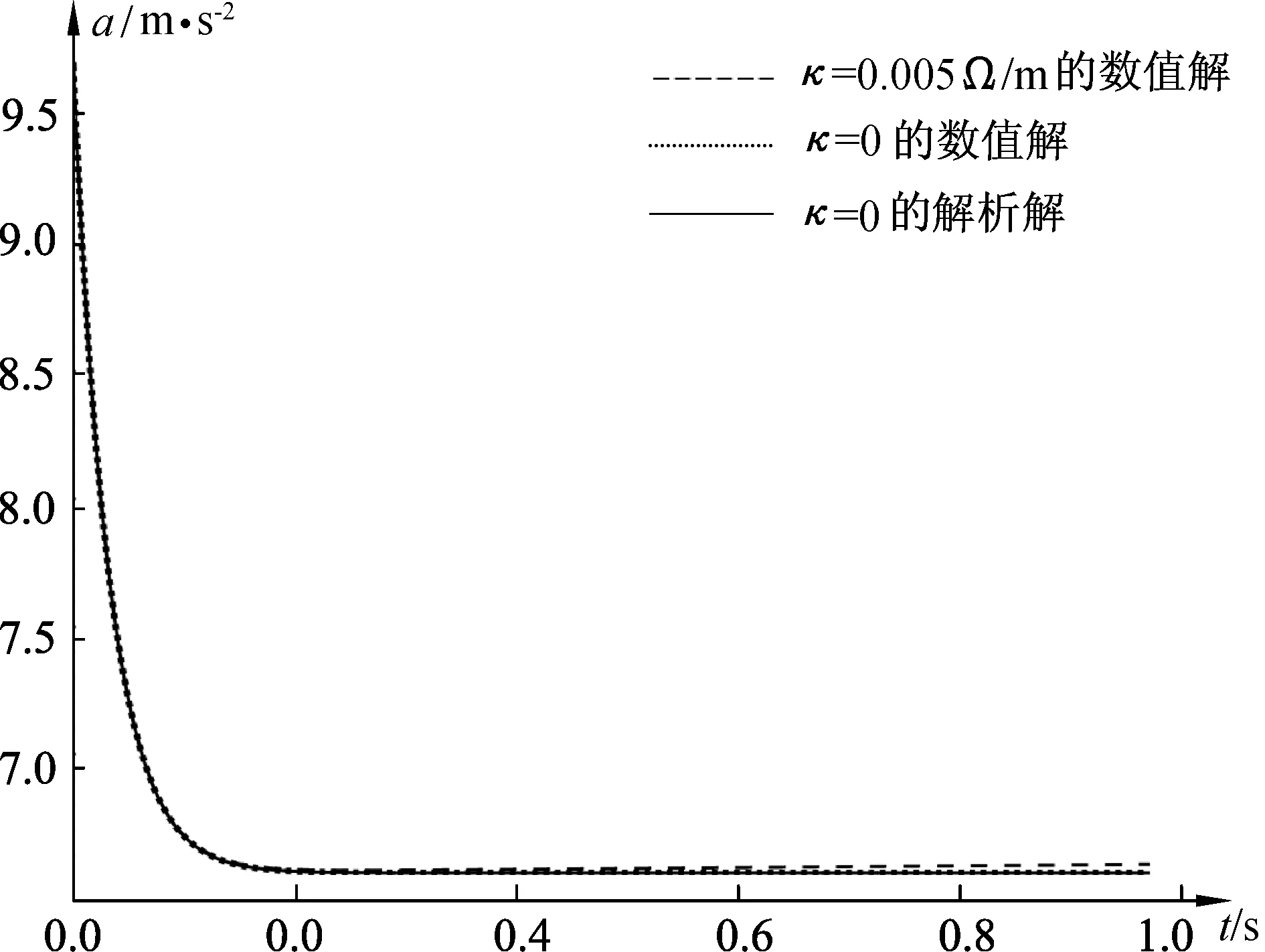
图8 当R0=0.1Ω时导轨电阻对金属棒加速度的影响

(2) 在R0=0.01Ω～3Ω范围内,κ=0.005Ω/m的结果(长划线)和κ=0的结果(点线)起初阶段是无差别的,但随着运动时间的增长(下落高度增大),两者的差别越来越明显,切合实际的计算应该从式(13)出发.但由于本问题中金属棒下落距离不长(仅为1.2m, 经历时间为0.5s～0.6s),本文第1节简化方法的计算结果已经很好地符合实际.

1 梁灿彬,秦光戎,梁竹健.电磁学[M].北京: 人民教育出版社,1980:3362-428.

2 王孟宁.电学中的几件“怪事”[J].物理通报,2004(1):7.

3 江俊勤. 基于Mathematica的数字化物理学[M]. 北京:科学出版社,2015: 132-136.

4 陶科.电磁感应现象中让人困惑情景的分析讨论[J].物理教师，2012(7)：13-14.

广东省高等学校物理专业综合改革试点项目(9010-15281).

2016-10-30)