乘积图的原子键连通性指数的上界

宋蕊，欧见平

（五邑大学 数学与计算科学学院，广东 江门 529020）

乘积图的原子键连通性指数的上界

宋蕊，欧见平

（五邑大学 数学与计算科学学院，广东 江门 529020）

原子键连通性指数是化学图论中比较重要的连通性指数，该指数已被广泛应用于研究烷烃的稳定性以及环烷烃的应变能等. 通过对乘积图的研究，给出了直积、析取和对称差的原子键连通性指数的上界，证明了这些上界是紧的，并且刻画了极图.

原子键连通性指数；直积；析取；对称差

1 引言与预备知识

设G是简单无向图，V(G)和E(G)分别表示其顶点集和边集，V(G)和E(G)的势叫做图G的顶点数和边数. 原子键连通性（atom-bond connectivity，ABC）指数是由Ernesto Estrada在1998年提出来的，连通图G的ABC指数的定义如下：

其中，d(u)和d(v)是顶点u和v的度数.

设G和H是简单无向图，图G和H的直积G×H、析取G∨H和对称差G⊕H的点集都为V(G)×V(H). 令点(a, b),(c, d)∈V(G)×V(H)，则：(a, b)(c, d)∈E(G×H)，当且仅当ac∈E(G)并且bd∈E(H)；(a, b)(c, d)∈E(G∨H)，当且仅当ac∈E(G)或者bd∈E(H)；(a, b)(c, d)∈E(G⊕H)，当且仅当ac∈E(G)或者bd∈E(H)；但不同时成立.

ABC指数已经被证明可以用来推测烷烃的能量信息[1-2]. 文献[3]给出了图和树的ABC指数的上下界，并且指出这些界都是可达的. 文献[4]中比较了化学树、分子图和一般图的GA指数和ABC指数. 文献[5-8]给出了ABC指数的一些数学性质. 文献[9]给出了关于两个图的联、复合、笛卡尔乘积、强积和纳米管乘积的ABC指数的若干不等式. 本文给出了图的直积、析取和对称差的ABC指数的上界，证明了这些上界是紧的，并且刻画了极图.

2 主要结果

2.1 直积的ABC指数

定理1设G和H是任意的两个连通、非平凡图，那么，等式成立当且仅当G和H都是正则图.

证明设u=(a, b),v=(c, d)是G×H的两个点. 则所以

式（1）中的等号成立当且仅当G和H都是正则图. 因此，

要使上式的等号成立，当且仅当对于任意的uv∈E(G×H)式（1）等式成立. 因此，定理得证.

2.2 析取的ABC指数

定理2设G和H是任意的两个连通、非平凡图，则

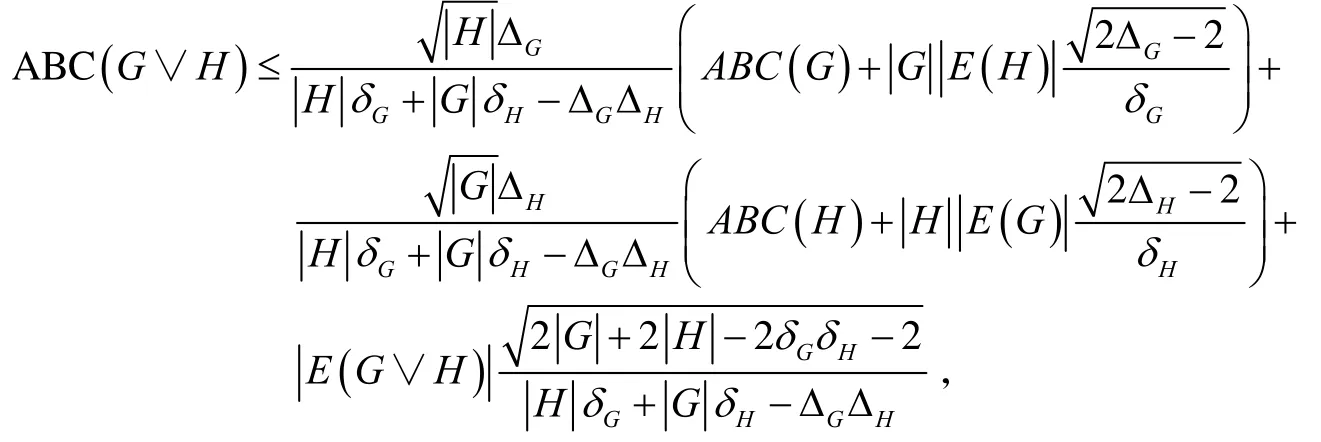
等式成立当且仅当G和H都是1-正则图.

证明设u=(a, b),v=(c, d)是G∨H的两个点. 则因此

上述不等式中的等号成立，当且仅当G和H都是正则图. 所以

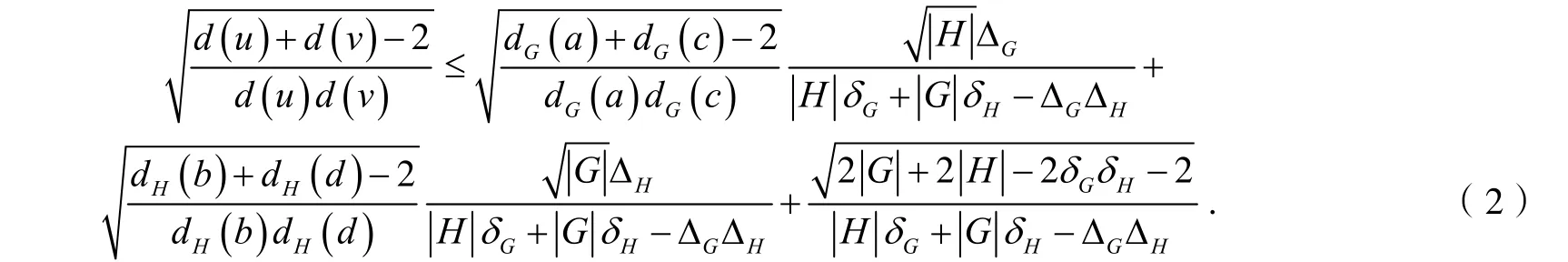
对正整数n归纳可以证明，对n个任意非负整数x1, x2,…,xn，都有，等式成立当且仅当x1, x2,…,xn中至少有n-1个等于零. 此结果表明：只有当G或H是1-正则图时，式（2）中等号才能成立. 但是，不等式（2）右边的第3项不可能与前两项同时等于零. 因此，只有当G和H都是1-正则图时，式（2）等号成立. 所以，

上述不等式中的等号成立，当且仅当G和H都是1-正则图. 因此，定理得证.

2.3 对称差的ABC指数

定理3设G和H是任意的两个连通、非平凡图，则

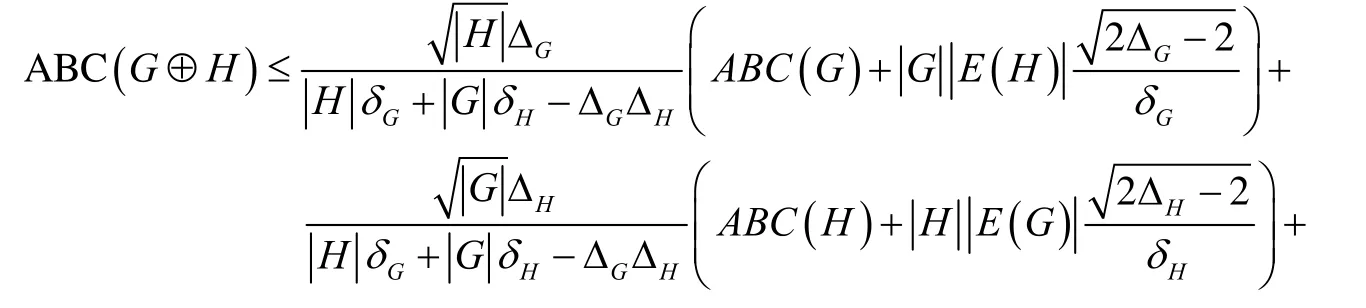
等式成立当且仅当G和H都是1-正则图.

证明设u=(a, b),v=(c, d)是G⊕H的两个点，则利用证明定理2类似的方法可得.

[1] ESTRADA E, TORRES L, RODRIGUEZ L, et al. An atom-bond connectivity index: modeling the enthalpy of formation of alkanes [J]. Indian J Chem, 1998, 37A: 849-855.

[2] ESTRADA E. Atom-bond connectivity and the energetic of branched alkanes [J]. Chem Phys Lett, 2008, 463(4-6): 422-425.

[3] DAS K C. Atom-bond connectivity index of graphs [J]. Discrete Appl Math, 2010, 158(11): 1181-1188.

[4] DAS K C, TRINAJSTIC N. Comparison between first geometric-arithmetic index and atom-bond connectivity index [J]. Chem Phys Lett, 2010, 497(1-3): 149-152.

[5] DAS K C, GUTMAN I, FURTULA B. On atom-bond connectivity index [J]. Chem Phys Lett, 2011, 511(4-6): 452-454.

[6] FURTULA B, GRAOVAC A. VUKICEVIC D. Atom-bond connectivity index of trees [J]. Discrete Appl Math, 2009, 157(13): 2828-2835.

[7] GRAOVAC A, GHORBANI M. A new version of atom-bond connectivity index [J]. Acta Chim Slov, 2010, 57: 609-612.

[8] XING Rundan, ZHOU Bo, DU Zhibin. Further results on atom-bond connectivity index of trees [J]. Discrete Appl Math, 2010, 158(14): 1536-1545.

[9] FATH-TABAR G H, VAEZ-ZADEH B, ASHRAFI A R, et al. Some inequalities for the atom-bond connectivity index of graph operations [J]. Discrete Appl Math, 2011, 159(13): 1323-1330.

[责任编辑：熊玉涛]

Upper Bounds for the Atom-bond Connectivity Index of Product Graphs

SONG Rui, OU Jian-ping
(School of Mathematics and Computationd Science, Wuyi University, Jiangmen 529020, China)

The atom-bond connectivity index is a relatively important connectivity index in the chemical graphs and has been applied to the study of the stability of alkanes and the strain energy of cycloalkanes. In this paper, the upper bounds for the atom-bond connectivity index of direct products, disjunction and symmetric differences of two graphs are presented. Those bounds are proven to be tight, and the extremal graphs are also characterized.

the atom-bond connectivity index; direct products; disjunction; symmetric differences

O157.5

A

1006-7302（2017）01-0001-04

2016-09-22

国家自然科学基金资助项目（11126326）；广东省自然科学基金资助项目（2014A030310413）；五邑大学研究生教育改革研究项目（YJS-JGXM-15-02）

宋蕊（1993—）女，甘肃平凉人，在读硕士生，主要研究方向为图的连通性理论；欧见平，教授，博士，硕士生导师，通信作者，主要从事图的连通性理论课题研究.