各国规范对深梁抗剪强度计算的比较

刘 恺，郑晓鹏，刘东旭

（ 温州市水利电力勘测设计院，浙江 温州 325000 ）

各国规范对深梁抗剪强度计算的比较

刘 恺，郑晓鹏，刘东旭

（ 温州市水利电力勘测设计院，浙江 温州 325000 ）

钢筋混凝土深梁具有较小的高跨比（或剪跨比），其破坏通常由受剪控制。然而其受力机理不同于一般梁，平截面假定对其并不适用。介绍了钢筋混凝土深梁受剪分析计算的方法，并对各国规范的相关内容进行简要说明。将中国规范的计算方法应用到549个简支混凝土深梁。结果表明，中国规范对高跨比小于2.00的深梁能够提供较为可靠的抗剪强度计算值（计算值与试验值之比的平均值为1.02，变异系数为25.1%），而对于高跨比大于2.00的梁的计算结果则离散性较大。对比各国规范计算结果发现，加拿大规范对钢筋混凝土抗剪强度计算提供最可靠的结果，美国规范在大多数情况下能提供较安全的结果，而中国规范和欧洲规范则未能提供相对安全的计算结果。同时发现，所有规范都未能提供对处于从深梁到一般梁过渡区域的梁的合理计算模型。

钢筋混凝土深梁；抗剪强度；规范；拉压杆模型

1 问题的提出

对于一般钢筋混凝土梁，通常采用平截面假定进行分析计算，即假定垂直与杆件轴线的各平截面因杆件受拉、受压或者受弯而产生变形后仍保持为平面，并且与变形后的杆件轴线垂直。根据这一假定，各平截面的应变分布情况只需要中性轴位置以及任一点的应变这2个参数即可确定，结合钢筋及混凝土的本构关系确定应力分布情况，从而获得内力及变形情况。这一计算分析方法简明清晰并已得到试验的广泛验证。但是当梁的长细比超出一定范围后，平截面假定便不再适用。图1 a所展示的长细比（L / h）为6.00的悬臂梁在收到水平荷载变形以后各平截面（横向短黑线）仍保持为平面并与梁轴线（竖向长黑线）垂直，但是当长细比减小至1.50（见图1），平截面在变形后出现明显的弯曲，说明该应变分布已不能由平截面假定描述。深梁指具有较小的剪跨比（a / d，见图2）的梁，剪跨比一般不大于3.00，具体各国规范略有不同。由于深梁的这一特征，其通常比普通梁具有更大的刚度和强度，用于承受较大的荷载，如高层建筑的转换梁、桥梁的墩台盖梁、墙式基础梁以及其它承重构件，其破坏由受剪情况决定。从20世纪50年代开始，国外即开展了对钢筋混凝土深梁的一系列试验研究，主要对其复杂的应力应变分布、受力机制以及影响其性能的关键因素等进行一系列研究。试验结果表明，不同于普通梁，深梁内部的压应力集中与从加载点到支座的对角区域，在破坏时通常沿着该对角线形成较宽的裂缝（见图3）。同时，由于深梁承受荷载大，其节点区域也可能产生局部受压破坏或者由于钢筋锚固不足产生的粘结破坏，但两者破坏可以通过加强局部抗压强度和加强钢筋锚固保证。对于钢筋混凝土深梁抗剪强度的计算，早期由于对深梁抗剪机理研究尚未深入，通常采用根据试验结果拟合出的经验公式。到20世纪80年代，德国学者将拉压杆模型应用到钢筋混凝土深梁来预测其抗剪强度，其后该方法得到了众多研究人员的推广和应用，并被纳入一些国家关于深梁抗剪的规范中。随着对深梁研究的深入，提出越来越多的方法，包括塑形理论的下限方法、神经网络方法、剪切板方法等。

图1 不同长细比悬臂梁在横向荷载下的变形图

图2 深梁的几何特征图

图3 深梁的破坏模式图

2 钢筋混凝土梁受剪分析计算的主要方法

2.1 一般钢筋混凝土梁的受剪分析方法

钢筋混凝土梁最早的分析计算模型是由Ritter和Morch在20世纪初提出的桁架模型（见图4 a）。该模型将有斜裂缝的钢筋混凝土梁看作一个桁架，将梁上部受压混凝土看作上弦杆，下部受拉钢筋看作下弦杆，横向箍筋看作竖向腹杆，斜裂缝间的受压混凝土看作斜腹杆，斜腹杆的角度被固定为45°。其后有学者指出该角度可以在一定范围内变化，从而提出变角桁架模型（见图4 b）。桁架的破坏可能是斜腹杆压碎或者是竖向腹杆的屈服。

同时学者也对钢筋混凝土梁的受剪情况进行了大量的试验分析，为提出基于试验结果的经验公式提供了可能。经验公式的提出经历了2个步骤：首先基于一定的理论分析提出影响钢筋混凝土梁的主要参数；对比试验结果拟合出以某些重要参数为变量的经验公式。对于钢筋混凝土梁，基于桁架模型首先认为梁的抗剪强度由2部分组成，即混凝土部分提供的抗剪强度Vc和钢筋部分提供的抗剪强度Vs。Vs通过桁架模型直接推导得出，而Vc则需要通过拟合大量试验结果得出。对于无箍筋梁，欧洲规范EC2给出了纯经验表达式。加拿大规范（CSA）采用了压力场模型，该模型包括了应变相容性和材料的应力应变关系，能够直接计算出腹板中主压应力的方向，同时模型还考虑了开裂混凝土的横向受拉影响。

2.2 钢筋混凝土深梁的抗剪分析方法

钢筋混凝土深梁可采用拉压杆模型进行分析。拉压杆模型实际上是对Ritter和Morch提出的经典桁架模型的推广。压杆代表了混凝土中应力相对集中的受压区域，拉杆代表了受拉钢筋，节点区域代表了应力复杂的拉杆和压杆交汇区域。拉压杆的方向并不是唯一固定的，选择在线弹性计算所得的主应力迹线附近（见图5）。如果拉压杆方向偏离线弹性分析结果较远，就要求结构具有形成较大的延性来实现内力重分布。与普通桁架类似，拉压杆模型的破坏可以是杆件破坏或者节点破坏。拉杆的强度等于受拉钢筋的面积与钢材屈服强度乘积。确定压杆和节点的尺寸及强度限值并不显而易见。对于平面尺寸问题有3种方法：一种是使得节点受压区域的2个主应力等于节点强度限值，这些区域被称作等静水压力区（虽然平面外应力为0）。节点区域及压杆尺寸可以一直增加到结构几何条件（如支座尺寸）的限制之内的最大值。另一种方法采用由支座尺寸、加载板、钢筋构造及其它几何条件确定尺寸固定的非等静水压力节点区域。荷载可以一直增加到节点或者杆件达到限值。还有一种可能的方法是将前2种方法相结合。

图 4 钢筋混凝土深梁抗剪的计算方法图

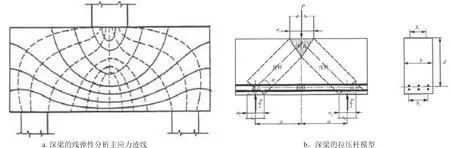
图 5 拉压杆模型的确定图

3 各国规范对深梁抗剪计算的规定

3.1 中国规范（CECS 39 : 92【2】和GB 50010 —2010【3】）

3.1.1 规范规定

CECS 39 : 92《钢筋混凝土深梁设计规程》规定，对跨高比l0/ h ≤ 2.00的简支梁和跨高比l0/ h ≤ 2.50 的连续梁，应按深梁设计。简支深梁的内力可按一般简支梁计算。对于深梁斜截面受剪承载力计算，其第2.3.2条规定深梁斜截面的受剪承载力应按下列公式计算：

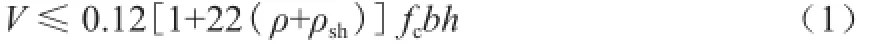
对于不满足要求的跨高比大于2.00的简支梁及跨高比大于2.50的连续梁，应作为一般梁按照GB 50010 — 2010《混凝土深梁设计规程》进行计算分析。规范第6.3.3条规定，不配置箍筋和弯起钢筋的一般板类受弯构件，其斜截面受剪承载力应符合下列规定：

式中：βh为截面高度影响系数：当h0小于800 mm时，取800 mm；当h0大于2 000 mm时，取2 000 mm。

规范第6.3.4条规定当仅配置箍筋时，矩形、T形和I形截面受弯构件的斜截面受剪承载力应符合下列规定：

式中：Asν为配置在同一截面内箍筋各肢的全部截面面积，即nAsν1，n为在同一个截面内箍筋的肢数，nAsν1为单肢箍筋的截面面积（mm2)；s为沿构件长度方向的箍筋间距（mm)；fyν为箍筋的抗拉强度设计值；Np0为计算截面上混凝土在预应力等于0时的预加力（kN)。

3.1.2 方法验证

参考Mihaylov等人[4]，本研究选取了其附录数据库中的549个简支钢筋混凝土深梁试验数据，并将其按照高跨比分为2类：l0/ h ≤ 2.00 的深梁和l0/ h＞2.00 的普通。深梁的抗剪强度按照CECS 39 : 92计算，一般梁的抗剪强度按照GB 50010 — 2010计算，为简单起见，按中国规范计算出梁抗剪强度统一记为VCECS。计算结果表明，按中国规范计算出的钢筋混凝土抗剪强度与试验获得的抗剪强度之比VCECS/VTEST，当剪跨比在2.00以内时，其平均值为1.02，变异系数为25.1%，当剪跨比大于2.00时，其平均值为0.85，变异系数为57.5%。由图5可以看出，当高跨比大于在2.00 ～8.00时，计算结果为最不安全，说明规范规定的计算方法可能并不适用于这一区间从深梁到一般梁的过渡区域。

3.2 其它国家规范

在此将要讨论的规范包括加拿大规范（CSA）[5]、美国规范（ACI）[6]和欧洲规范（EC2）[7]。对于一般钢筋混凝土梁的抗剪强度计算，CSA规范采用了压力场模型，ACI规范则采用了基于桁架模型的试验拟合公式，而EC2规范则采用了纯经验公式。对于钢筋混凝土深梁的抗剪强度计算，此3规范都包括了拉压杆模型，具体设计流程类似，但也存在如下不同：首先是结点区域和压杆的强度折减系数各个规范有所不同；其次是压杆的倾斜角度有所不同。CSA规范基于压力场理论对压杆的倾角进行计算，并根据倾角的不同对拉压杆结构的强度进行调整。ACI和EC2规范仅依靠强度折减系数而非压杆倾斜的角度来调整拉压杆结构的强度。ACI规范认为压杆倾角越小深梁抗剪承载力越弱，因此限制了拉压杆模型的压杆倾角不得小于25°。2008年Collins[8]等人分别采用这几种规范规定的计算方法对大量钢筋混凝土梁进行计算，结果见图6，应注意横坐标为剪跨比（a /d，见图2）。

图 5 中国规范计算方法验证图

图 6 各国规范的抗剪强度方法验证图

由图6可以看出，按照加拿大规范的计算结果最为可靠，离散度最小。中国规范在深梁范围内计算结果过于保守，可能与中国规范提供的是经验表达式而非拉压杆等物理模型有关，使得结构设计的经济性下降。欧洲规范和中国规范在一般梁范围内的计算结果偏于不安全，美国规范与前2个规范相比较为可靠。所有规范的计算结果都体现出一个共同的规律，即在从深梁到一般梁的过渡区域计算结果相对较为离散，说明几乎所有规范提供的方法都不能完全适应处于过渡区的钢筋混凝土梁的抗剪计算。

4 结 语

介绍了钢筋混凝土深梁在剪力作用下的受力机理、抗剪强度研究方法以及各国规范中所采用的方法。将中国规范规定的深梁及一般梁的抗剪强度计算方法应用于549个简支梁，结果表明对于高跨比在2.00以内的深梁，中国规范能够提供较好的预测结果：计算值与试验值之比的平均值为1.02，变异系数为25.1%；而对于高跨比大于2.00的梁而言，其计算结果的离散性很大，变异系数超过了50.0%，主要是因为高跨比大于2.00的梁包括从深梁到一般梁过渡的梁，对于这部分梁，规范中没有尚未包括合理的计算方法，因此导致结果有较大的离散性。对其它国家的规范也作出了简要介绍，包括加拿大CSA 规范、美国ACI规范和欧洲EC2规范，这3个规范对于钢筋混凝土深梁都采用了拉压杆物理模型。对比计算结果而言，加拿大规范提供了显著优于其它各规范的计算结果，美国规范在大部分范围内均能保证计算结果的安全性，中国规范和欧洲规范计算结果的安全性则难以保证。同时值得注意的是，几乎所有规范都未能在从深梁到一般梁的过渡区域提供与其它区域同样精度的计算结果，说明所有规范都未包括对于过渡区梁的合理计算模型。

[1] Lee，Duncan Ding Kan．An experimental investigation of the effects of detailing on the shear behaviour of deep beams[D]．不详，1982．

[2] 华南理工大学．CECS39：92钢筋混凝土深梁设计规程[S]．北京：中国建筑工业出版社，2002．

[3] 中华人民共和国住房与城乡建设部．GB 50010 — 2010钢筋混凝土结构设计规范[S]．北京：中国建筑工业出版社，2010．

[4] Mihaylov，B．I.,Bentz，E．C.,Collins，M．P．Two - Parameter Kinematic Theory for Shear Behavior of Deep Beams[J]．ACI Structural Journal，2013，110(3)：447 - 456．

[5] CSA Committee A23．3．Design of Concrete Structures，Canadian Standards Association[S]．Mississauga，Ontario：Canadian Standards Association，2005．

[6] ACI Committee 318．Building Code Requirements for Reinforced Concrete (ACI 318 - 08) and Commentary (318 R - 08) [S]．Farmington Hills American： Concrete Institute465，2008．

[7] European Committee for Standardization，CEN，EN 1992 - 1 - 1．Eurocode 2：Design of Concrete Structures - Part 1 - 1：General Rules and Rules for Buildings[S]．Brussels，Belgium：Eurepean Committee for stand ardization，2004：225．

[8] Collins，M．P.,Bentz，E．C.,Sherwood，E.G．Where is Shear Reinforcement Required? Review of Research Results and Design Procedures，ACI Structural Journal，2008，105(5)：589 - 599．

（责任编辑 郎忘忧）

Comparison of Shear Strength Calculation for Deep Beams Using Different Codes

LIU Kai，ZHENG Xiao - peng，LIU Dong - xu
（Wenzhou Design Institute of Water Conservancy and Electric Power，Wenzhou 325000，Zhejiang，China）

TReinforced concrete (RC) deep beam is characterized by small height - span ratio.The failure of deep beam is usually controlled by shear.Different from slender beams，deep beams have disturbed stress/strain fi eld，so the assumption that “plane keeps plane” does not work for deep beams.This study first explains calculation methods for RC deep beams and then gives brief introduction on relevant regulations in different codes.The calculation method in Chinese code is applied to 549 simply - supported deep beams，and the results show that Chinese code can provide reliable prediction for deep beams with height - span ratio smaller than 2.00，while out of this range the prediction is quite scattered.The calculation results from other codes are compared also.It is found that the Canadian code provides the most reliable and accurate results，and American code can provide safe results in most of the cases，while predictions based on European code and Chinese code can be very unsafe.It is also very interesting to point out that almost all the codes need a better model for the beams located in the transfer zone from deep beams to slender beams.

RC deep beams；shear strength；strut - and - tie model；empirical formula

TU375

A

1008 - 701X(2017)02 - 0049 - 05

10.13641/j.cnki.33 - 1162/tv.2017.02.014

2016 - 02-17

刘 恺(1985-)，男，工程师，大学本科，主要从事水利工程设计工作。