基于混合高斯模型的相关非高斯输入变量随机潮流计算

黄 煜 徐青山 刘建坤 卫 鹏

(1东南大学电气工程学院, 南京 210096)(2江苏省电力公司电力科学研究院, 南京 210003)

基于混合高斯模型的相关非高斯输入变量随机潮流计算

黄 煜1徐青山1刘建坤2卫 鹏2

(1东南大学电气工程学院, 南京 210096)(2江苏省电力公司电力科学研究院, 南京 210003)

提出一种考虑输入变量相关性的随机潮流计算方法.该方法针对系统中的非高斯输入变量,建立其混合高斯模型(GMM).在此基础上,引入高斯分量组合算法(GCCM),通过多次加权最小二乘计算(WLS)直接求得输出变量的概率分布.研究限制GMM中高斯分量个数的约简方法,以减少WLS运算次数.对IEEE-30节点系统的仿真和误差分析表明,GMM具有拟合精度高、适用性广的特点.所提方法与MCS的计算结果基本一致,但计算效率有了显著提高,并且算法的速度和精度与WLS运算次数有关.

混合高斯模型;约简算法;相关性;高斯分量组合;随机潮流

近年来,以风电为代表的新能源发电在我国得到了大力发展[1-2].由于风机出力具有强随机性、弱可控性,因而其大规模接入将给电网运行带来许多不确定因素[3].而分布式电源及储能的发展、电动汽车的兴起以及电力市场的逐步建立则将加剧系统的不确定性[4-6].

另一方面,实际电力系统中还需考虑各种关联因素的影响,如同一地区的同类负荷受自然或社会因素的影响具有相似的波动特性,地理位置相近的风电场之间风速具有强相关性(同时增大或减小)等[7-8],随着能源互联网概念的提出[9],未来电网中各部分的联系将愈加紧密.为了应对新环境下电网呈现出的随机性和相关性的挑战,准确评估系统的潮流分布特性是基础和前提.

近些年,大量国内外学者在Borkowska等[10]提出的随机潮流基础上考虑相关性因素.目前,相关性的随机潮流方法有蒙特卡洛仿真法(MCS)、点估计法(PEM)[11-12]和半不变量法[13]等.以简单随机采样为基础的传统MCS除了原理简单、精度高的优势外,还能方便地与ARMA模型和时移技术[14]、Nataf变换[15]、Copula函数等相关性问题的处理方法相结合,但计算规模大、耗时长,即使采用改进的抽样技术,如拉丁超立方采样[16]、准蒙特卡洛法等,计算负担仍很重,这也制约了其进一步发展.而点估计法和半不变量法与MCS相反,文献[17-18]通过Cholesky分解在上述方法的基础上考虑输入变量之间的相关性,但当系统规模较大时,其有效性及误差大小有待进一步验证.文献[19]将不确定度量化的方法用于随机潮流中,采用基于广义正交多项式混沌(gPC)的随机Galerkin法,将随机潮流方差转化为一组确定性的高维方差,通过一次求解代替MCS的反复计算,具有较高的计算精度.

由于系统的随机输入变量,如负荷功率、风电机组出力等大多是非高斯分布,难以用单一的标准分布函数准确拟合[20],使得PEM所得高阶矩误差较大,并给输入变量的各阶半不变量求解带来困难.文献[21-23]采用高斯分布来近似不同类型的负荷,由此产生的建模误差会带入到随机潮流计算中,并在误差传递作用下放大[24],影响结果的精度.

本文提出了采用混合高斯模型(Gaussian mixture model, GMM)描述系统的相关非高斯输入变量,能够适应各种分布类型且拟合精度较高.并在此模型基础上,引入高斯分量组合算法(Gaussian component combination method, GCCM),通过多次加权最小二乘运算(weighted least square, WLS)得到各节点电压和支路潮流的概率分布(PDF).为了减少WLS计算次数,研究不同的约简方法以限制GMM的高斯分量个数.通过对IEEE-30节点系统的测试,验证了所提方法的准确性和实用性.

1 混合高斯模型

GMM是由若干个高斯分布加权线性叠加而成,对于一维随机变量X,其PDF可表示为[25]

(1)

式中,ωi,μi和σi分别为GMM中第i个分量的权重、均值和标准差.其中,权重系数ωi必须满足归一化条件,即

(2)

通过EM算法[26]并结合量测数据可以方便地求得参数ω,μ和σ.而高斯分量个数n会直接影响模型的精确程度,n越大,模型的偏差越小.理论上,当n→∞时,GMM能够平滑任何类型的输入变量分布,但待求参数和耗时也增大.应用AIC信息准则[27]能够较好地平衡模型复杂度与拟合准确性之间的矛盾,从而得到n的最佳取值.图1为采用GMM(n=4)近似非高斯的实际负荷样本分布.为了评估GMM的拟合效果,选取3种常用分布(高斯分布、对数高斯分布和γ分布)作为参照(见图2),可以看出,GMM的拟合精度明显优于其他分布.卡方检验[28]可用于拟合优度的量化分析,卡方值越小,说明函数的拟合效果越好.表1列出了不同拟合分布卡方值的大小(利用Matlab中的chi2gof函数),其中GMM的卡方值远小于其他3种分布,证明了其建模的准确性.

图1 实际负荷的混合高斯模型近似

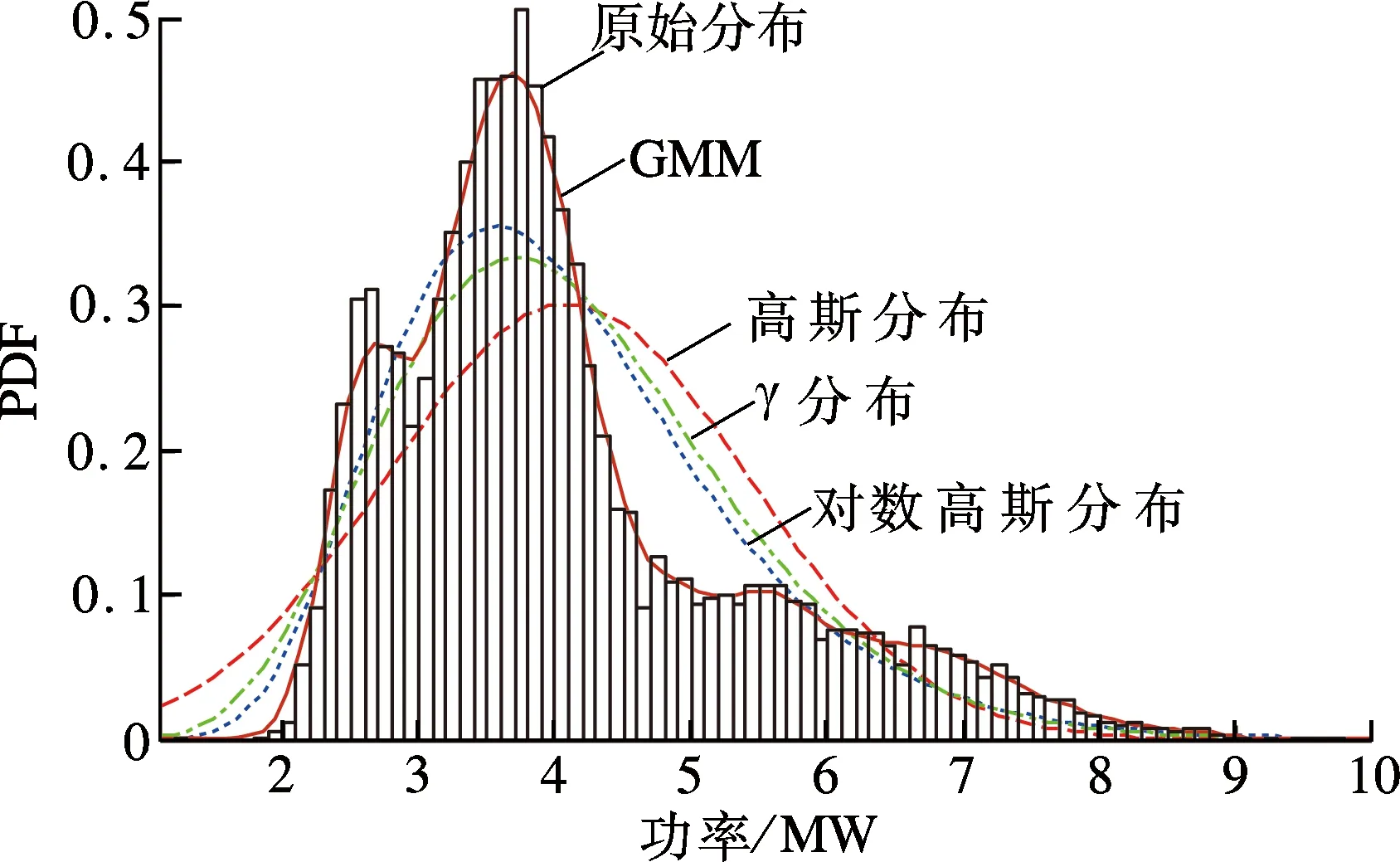
图2 不同拟合曲线的比较

表1 各种分布的卡方检验

2 高斯分量的约简

当系统中采用GMM所表示的非高斯输入变量较多时,随机潮流计算规模会随高斯分量个数n的增大成几何倍数甚至指数式的增长.因此,在基本不丢失拟合精度的前提下,采用约简算法以减少高斯分量的个数n.约简算法主要应满足以下三点准则:

1) 保持约简前后的均值和方差不变,即使有偏差也很小,可忽略不计.

2) 算法本身便捷有效、鲁棒性好.

3) 约简后的结果应当与初始模型具有类似的结构或形式上一致.

一般的约简方法,如文献[29]的整体合并和聚类合并能够满足上述准则1或2,但约简得到的结果均为单一的高斯分布,在形式上与原GMM有一定差异.为了满足准则3的要求,本文采用配对合并的方法,设约简后的结果为gX(x),可表示为

(3)

Jd=∫(fX(x)-gX(x))2dx

(4)

式(4)可进一步展开为

Jd=Jd,ff-2Jd,fg+Jd,gg

(5)

其中,Jd,ff=∫fX(x)2dy,Jd,fg=∫fX(x)gX(x)dx,Jd,gg=∫gX(x)2dx.结合式(1)、(3)中的fX和gX的具体表达式,可得

2个高斯函数乘积的积分可表示为[30]

(9)

式中,α为尺度参数,

(10)

(11)

(12)

用式(9)替换式(6)～(8)中的积分项,经化简后得到

(13)

(14)

(15)

将gX中所有分量两两配对组合,使Jd最小的一对分量i,j合并,得到新的高斯分量ij的各个参数为

(16)

(17)

(18)

完成一次配对合并,gX减少一个分量,但均值和方差保持不变.重复以上步骤,直到高斯分量个数n达到指定值.图3为配对合并后所得gX(l=2,3)的曲线,相较于前2种约简方法,其与原GMM分布基本吻合,拟合效果最好.

图3 不同约简模型的比较

3 非高斯输入变量的随机潮流

3.1 高斯分量组合算法

Dopazo等[31]借鉴了状态估计的思想,利用WLS进行随机潮流计算,但所有输入变量必须服从高斯分布.针对用GMM近似的非高斯输入变量,本文提出一种高斯分量组合算法(GCCM).从各GMM中每次选取一个高斯分量并进行WLS运算,共有Nc种高斯分量的组合方式,总的WLS运算次数为

(19)

式中,N为非高斯输入变量的个数；Li为第i个GMM所含高斯分量的个数.若Li=1,i=1,2,…,N,则意味着所有输入变量的PDF都简化为高斯分布,此时只需要一次WLS运算.

就单次运算,WLS方法的关键是最小化如下目标函数:

J(x)=[z-h(x)]TR-1[z-h(x)]

(20)

式中,x为由节点电压幅值和相角组成的向量；z为输入变量向量(高斯分量的均值)；h(x)由一系列非线性的节点电压量测方程组成；R为输入向量z的误差协方差矩阵.

矩阵R的对角元素为对应的高斯分量的方差,而非对角元素反映的是不同输入变量间的相关性.假设任意2个高斯分量的相关性与它们各自所属的GMM间的相关性保持一致,则非对角元素R(i,j)可表示为

R(i,j)=ρijσiσj

(21)

式中,σi,σj为高斯分量i或j的标准差；ρij为第i,j个输入变量之间的相关系数.通过迭代搜寻使式(20)的最优状态估计值最小,第k次迭代的表达式为

G(xk)Δxk=HT(xk)R-1[z-h(xk)]

(22)

式中,H=(∂h(x)/∂x)；G=HTR-1HT为信息矩阵.当Δxk=xk+1-xk小于设定值时,迭代终止.由求得的状态量可进一步计算出系统的支路潮流及各节点的注入量.

对信息矩阵G求逆，可以得到状态量x的协方差矩阵Σs,即

Σs=[HT(x)R-1HT(x)]-1

(23)

相应地,支路潮流和部分节点注入量的协方差矩阵Σp可表示为

Σp=K(x)G-1(x)KT(x)

(24)

式中,K(x)=(∂k(x)/∂x),k(x)为包含支路潮流及节点注入量的量测方程.

(25)

最终建立节点电压幅值、相角及支路潮流的PDF表达式为

(26)

3.2 算法流程

GCCM算法求解随机潮流的流程如图4所示,可归纳为以下几步:

① 分别从GMM拟合的各输入变量中选取一个高斯分量,形成一种组合方式.每个高斯分量的均值作为输入变量向量z的一个元素,方差为误差协方差矩阵R相应的对角元素.考虑输入变量的相关性,由式(21)修正R中的非对角元素.

② 通过WLS得到系统节点电压、支路潮流及部分节点注入量的最优估计值,并储存式(23)、(24)所得协方差矩阵Σs和Σp的对角元素.

④ 重复步骤①～③,直到输入变量的所有高斯分量组合方式都完成遍历.最终Nc个高斯分量按式(26)建立输出变量的PDF.

GCCM的耗时主要取决于WLS运算次数Nc.如果Nc较大,则需要在对非高斯输入变量建模后,采用2.3节的方法约简GMM中高斯分量的个数.由式(19)可知,对于输入变量个数Nc较多的大型系统,每约简一个高斯分量,Nc会显著减小,相应的计算时间也随之减少.

图4 GCCM随机潮流计算方法的流程图

4 算例分析

4.1 仿真系统介绍

由于WLS计算误差一般与系统规模关系不大[31],为了便于说明问题,以改进的IEEE-30节点系统为例,网络结构与线路参数详见文献[32].在节点24,29处分别接入2座装机容量为10,35 MW的小型风电场,其有功功率采用GMM拟合,具体参数如表2所示.采用恒功率因数控制方式(φ=0.95),风电场之间的出力具有相关性,相关系数ρ=0.6.

表2中GMM参数的确定需要大量的风电场历史统计数据,若缺少必要的量测数据,则通常先利用标准分布函数(如Weibull分布)来近似风速分布,并结合风电机组的输出特性,得到风电场出

力的概率分布[33].由于风速拟合过程中不可避免地会产生误差,在风机输出特性的传递作用下,该误差将被放大,导致模型精度不高.

表3给出了采用GMM拟合的负荷模型参数,一般高斯分量n取2或3即可达到AIC信息准则的收敛要求.假定负荷有功与无功之间的功率因数角恒定,有

(27)

式中,μP,σP为有功功率高斯分量的均值和标准差；φ为功率因数角.

表2 风电场有功功率的GMM参数 p.u.

表3 负荷有功功率的GMM参数 p.u.

除节点4,7和21外,其余节点负荷功率均服从高斯分布,均值见文献[32]的负荷数据,标准差取均值的10%.考虑节点负荷之间的相关性,可将系统大致分为2个区域:区域1包含节点16～20,相关系数ρ1=0.6；区域2(节点15,23～26)的相关系数ρ2=0.75,2个区域间存在弱相关性(ρ1,2=0.2).

4.2 仿真结果与误差分析

采用GCCM对上述算例进行仿真计算,为了比较负荷的GMM及高斯模型对随机潮流结果的影响,利用下式将表3中的节点负荷模型替换为与原GMM相等的高斯分布的均值和方差：

(28)

(29)

以MCS所得结果作为参照(样本规模NL=2×104),图5为节点25电压幅值U25及支路19-20无功功率的CDF曲线比较.由图可知,采用GMM求得的概率分布曲线非常接近于MCS方法的概率分布,而高斯模型的概率分布与MCS存在一定偏差.

对上述误差做定量分析,引入方差和的根均值(average root mean square,ARMS)来衡量输出变量概率分布的计算精度[34],即

(30)

(a) 节点25电压幅值的CDF

(b) 支路19-20无功功率的CDF

为了减少WLS的运算次数,采用配对合并方法对表2中GMM拟合风电场有功出力进行高斯分量的约简,将高斯分量个数L从5降至4，最后降到3,则对应的WLS次数Nc=300,192和108(取决于所有GMM的高斯分量组合数).

表4 部分输出变量的ARMS %

图6(a)比较了约简前后节点26电压幅值的PDF.可以明显看出,Nc=300和192所对应的PDF与MCS的结果较为接近,而当WLS次数Nc降至108时,经约简所带来的拟合误差影响开始显现,尽管得到的PDF曲线形状上仍保持一致,但精度有所损失.

图6(b)给出的支路10-17无功功率的变化规律与图6(a)的电压幅值变化规律正好相反:WLS次数越少,其PDF反而越接近MCS的结果.这是由于所提方法假设相关系数ρij在每次WLS计算中固定不变(即任意2个高斯分量的相关性与它们各自所属的GMM间的相关性一致),导致每次运算都会引入误差,而减小Nc能有效避免这种误差的影响.

(a) 节点26电压幅值的PDF

(b) 支路10-17无功功率的PDF

表5列出了系统输出变量均值μ和标准差σ的平均相对误差[35].可以看出，均值的相对误差都很小，且与Nc关系不大，而对标准差σ而言,Nc越大,误差传递的次数越多,标准差的相对误差也就越大.

表5 均值和标准差的平均相对误差 %

在主频为2.63 GHz、运行内存为2 GB的intel i3计算机上,采用Matlab 2012b运行得到算法的计算时间如表6所示.当Nc=300时,其耗时约为MCS(NL=2×104)的3%,且随Nc的减小,耗时呈线性下降,极大地提升了计算效率.

表6 算法的计算时间对比 s

5 结论

1) 与其他标准分布相比,GMM的拟合精度更高,且模型灵活简单、参数确定较为方便.

2) 所提方法的计算耗时相较于MCS有了显著降低,通过对高斯分量约简,减少了GCCM中WLS运算次数,可进一步加快计算速度.

3) 利用误差协方差矩阵中的非对角元素,能方便地处理输入变量之间的相关性.

4) 由于算法假设高斯分量间的相关系数在计算过程中固定不变,故每次WLS运算都会引入误差.约简高斯分量个数虽然使模型精度下降,但也减少了WLS运算次数,减小了误差传递的影响,在某些场合反而能提高精度.

虽然本文的约简方法有效地提升了计算效率,但当系统规模巨大,随机变量数量众多,维数升高时,所提算法的计算量会显著增加.后续将研究通过高性能并行计算或分布式计算策略,实现所提算法在实际大规模场景下的在线应用.

References)

[1]王深哲,高山,李海峰,等.含风电接入的电网规划方案电能质量评估[J].电工技术学报,2013,28(8):56-65. DOI:10.3969/j.issn.1000-6753.2013.08.008. Wang Shenzhe, Gao Shan, Li Haifeng, et al. Evaluation of power quality in grid planning scheme with wind power integration[J].TransactionsofChinaElectrotechnicalSociety, 2013, 28(8): 56-65. DOI:10.3969/j.issn.1000-6753.2013.08.008. (in Chinese)

[2]Xu Q, Kang C, Zhang N, et al. A probabilistic method for determining grid-accommodable wind power capacity based on multiscenario system operation simulation[J].IEEETransactionsonSmartGrid, 2016, 7(1): 400-409. DOI:10.1109/tsg.2014.2381271.

[3]边巧燕,徐开,孙黎滢,等.考虑风电功率概率分布不确定性的输电系统规划[J].电力系统自动化,2015,39(20):60-65. DOI:10.7500/AEPS20141029009. Bian Qiaoyan, Xu Kai, Sun Liying, et al. Transmission system planning method considering wind power probability distribution[J].AutomationofElectricPowerSystems, 2015, 39(20): 60-65. DOI:10.7500/AEPS20141029009. (in Chinese)

[4]Vardakas J S, Zorba N, Verikoukis C V. A survey on demand response programs in smart grids: Pricing methods and optimization algorithms[J].IEEECommunicationsSurveys&Tutorials, 2015, 17(1): 152-178. DOI:10.1109/comst.2014.2341586.

[5]Jhala K, Natarajan B, Pahwa A, et al. Coordinated electric vehicle charging solutions using renewable energy sources[C]//2014IEEESymposiumonComputationalIntelligenceApplicationsinSmartGrid. Orlando, USA: IEEE, 2014: 1-6.

[6]侯婷婷.含大规模风电的电力系统储能电源优化配置研究[D].武汉:华中科技大学电气工程学院,2014.

[7]Haessig P, Multon B, Ben Ahmed H, et al. Energy storage sizing for wind power: Impact of the autocorrelation of day-ahead forecast errors[J].WindEnergy, 2015, 18(1): 43-57.

[8]吴耀武,张联邦,李海英,等.考虑多风电场出力相关性的风电容量可信度评估方法[J].电力自动化设备,2015,35(11):8-12. DOI:10.16081/j.issn.1006-6047.2015.11.002. Wu Yaowu, Zhang Lianbang, Li Haiying, et al. Wind-power capacity credibility assessment considering power output correlation of multiple wind farms[J].ElectricPowerAutomationEquipment, 2015, 35(11): 8-12. DOI:10.16081/j.issn.1006-6047.2015.11.002. (in Chinese)

[9]赵海,蔡巍,王进法,等.能源互联网架构设计与拓扑模型[J].电工技术学报,2015,30(11):30-36. DOI:10.3969/j.issn.1000-6753.2015.11.005. Zhao Hai, Cai Wei, Wang Jingfa, et al. An architecture design and topological model of intergrid[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(11): 30-36. DOI:10.3969/j.issn.1000-6753.2015.11.005. (in Chinese)

[10]Borkowska B. Probabilistic load flow[J].IEEETransactionsonPowerApparatusandSystems, 1974, 93(3): 752-759. DOI:10.1109/tpas.1974.293973.

[11]吴巍,汪可友,韩蓓,等.基于Pair Copula的随机潮流三点估计法[J].电工技术学报,2015,30(9):121-128.DOI:10.3969/j.issn.1000-6753.2015.09.016. Wu Wei, Wang Keyou, Han Bei, et al. Pair Copula based three-point estimate method for probabilistic load flow calculation[J].TransactionsofChinaElectrotechnicalSociety, 2015, 30(9): 121-128. DOI:10.3969/j.issn.1000-6753.2015.09.016.(in Chinese)

[12]Zhang Y, Lam J S L. A copula approach in the point estimate method for reliability engineering[J].QualityandReliabilityEngineeringInternational, 2015, 32(4): 1501-1508. DOI:10.1002/qre.1860.

[13]石东源,蔡德福,陈金富,等.计及输入变量相关性的半不变量法概率潮流计算[J].中国电机工程学报,2012,32(28):104-113. Shi Dongyuan, Cai Defu, Chen Jinfu, et al. Probabilistic load flow calculation based on cumulant method considering correlation between input variables[J].ProceedingsoftheCSEE, 2012, 32(28): 104-113. (in Chinese)

[14]Foley A M, Leahy P G, Marvuglia A, et al. Current methods and advances in forecasting of wind power generation[J].RenewableEnergy, 2012, 37(1): 1-8. DOI:10.1016/j.renene.2011.05.033.

[15]Chen Y, Wen J, Cheng S. Probabilistic load flow method based on Nataf transformation and Latin hypercube sampling[J].IEEETransactionsonSustainableEnergy, 2013, 4(2): 294-301. DOI:10.1109/tste.2012.2222680.

[16]黄煜,徐青山,卞海红,等.基于拉丁超立方采样技术的半不变量法随机潮流计算[J].电力自动化设备,2016,36(11):112-119. Huang Yu, Xu Qingshan, Bian Haihong, et al. Cumulant method based on Latin hypercube sampling for calculating probabilistic power flow[J].ElectricPowerAutomationEquipment, 2016, 36(11): 112-119. (in Chinese)

[17]陈雁.含大规模风电场电力系统的运行与规划方法研究[D].武汉:华中科技大学电气工程学院,2012.

[18]Ai X, Wen J, Wu T, et al. A discrete point estimate method for probabilistic load flow based on the measured data of wind power[J].IEEETransactionsonIndustryApplications, 2013, 49(5): 2244-2252. DOI:10.1109/tia.2013.2262254.

[19]李怡宁,吴浩,辛焕海,等.基于广义多项式混沌法的电力系统随机潮流[J].电力系统自动化,2015,39(7):14-20. DOI:10.7500/AEPS20140817003. Li Yining, Wu Hao, Xin Huanhai, et al. Power system probabilistic load flow based on generalized polynomial chaos methods[J].AutomationofElectricPowerSystems, 2015, 39(7): 14-20. DOI:10.7500/AEPS20140817003. (in Chinese)

[20]Heunis S W, Herman R. A probabilistic model for residential consumer loads[J].IEEETransactionsonPowerSystems, 2002, 17(3): 621-625. DOI:10.1109/tpwrs.2002.800901.

[21]苏胜皓,宋锐,陈庆芳,等.基于序列运算的含分布式发电配电网潮流分析[J].电力系统保护与控制,2014,42(24):12-17. Su Shenghao, Song Rui, Chen Qingfang, et al. Power flow analysis of distribution network containing distributed generation based on sequence operation[J].PowerSystemProtectionandControl, 2014, 42(24): 12-17. (in Chinese)

[22]Aien M, Fotuhi-Firuzabad M, Rashidinejad M. Probabilistic optimal power flow in correlated hybrid wind—photovoltaic power systems[J].IEEETransactionsonSmartGrid, 2014, 5(1): 130-138.

[23]董雷,程卫东,杨以涵.含风电场的电力系统概率潮流计算[J].电网技术,2009,33(16):87-91. Dong Lei, Cheng Weidong, Yan Yihan. Probabilistic load flow calculation for power grid containing wind farms[J].PowerSystemTechnology, 2009, 33(16): 87-91. (in Chinese)

[24]Lange M. On the uncertainty of wind power predictions—Analysis of the forecast accuracy and statistical distribution of errors[J].JournalofSolarEnergyEngineering, 2005, 127(2): 177-184. DOI:10.1115/1.1862266.

[25]Reynolds D. Gaussian mixture models[M] //EncyclopediaofBiometrics. Maryland, USA: Springer, 2009: 659-663.

[26]王爱平,张功营,刘方.EM算法研究与应用[J].计算机技术与发展,2009,19(9):108-110. DOI:10.3969/j.issn.1673-629X.2009.09.030. Wang Aiping, Zhang Gongying, Liu Fang. Research and application of EM algorithm[J].ComputerTechnologyandDevelopment, 2009, 19(9): 108-110. DOI:10.3969/j.issn.1673-629X.2009.09.030. (in Chinese)

[27]Yamaoka K, Nakagawa T, Uno T. Application of Akaike's information criterion (AIC) in the evaluation of linear pharmacokinetic equations[J].JournalofPharmacokineticsandBiopharmaceutics, 1978, 6(2): 165-175. DOI:10.1007/bf01117450.

[28]Singh R, Pal B C, Jabr R. Statistical representation of distribution system loads using Gaussian mixture model[J].IEEETransactionsonPowerSystems, 2010, 25(1): 29-37. DOI:10.1109/tpwrs.2009.2030271.

[29]Singh R, Pal B C, Jabr R A. Statistical representation of distribution system loads using Gaussian mixture model[J].IEEETransactionsonPowerSystems, 2010, 25(1): 29-37. DOI:10.1109/tpwrs.2009.2030271.

[30]Williams J L, Maybeck P S. Cost -function-based Gaussian mixture reduction for target tracking[C]//ProceedingsoftheSixthInternationalConferenceofInformationFusion. Cairns, Australia, 2003, 2: 1047-1054. DOI:10.1109/icif.2003.177354.

[31]Dopazo J F, Klitin O A, Sasson A M. Stochastic load flows[J].IEEETransactionsonPowerApparatusandSystems, 1975, 94(2): 299-309. DOI:10.1109/t-pas.1975.31855.

[32]Christie R. Power system test archive [EB/OL]. (1999)[2016-01]. http://www.ee.washington.edu/research/pstca.

[33]蒋程,刘文霞,张建华,等.含风电接入的发输电系统风险评估[J].电工技术学报,2014,29(2):260-270. DOI:10.3969/j.issn.1000-6753.2014.02.032. Jiang Cheng, Liu Wenxia, Zhang Jianghua, et al. Risk assessment of generation and transmission systems considering wind power penetration[J].TransactionsofChinaElectrotechnicalSociety, 2014, 29(2): 260-270. DOI:10.3969/j.issn.1000-6753.2014.02.032. (in Chinese)

[34]Zhang P, Lee S.T. Probabilistic load flow computation using the method of combined cumulants and Gram-Charlier expansion[J].IEEETransactionsonPowerSystems, 2004, 19(1): 676-682. DOI:10.1109/tpwrs.2003.818743.

[35]Cai D, Shi D, Chen J. Probabilistic load flow with correlated input random variables using uniform design sampling[J].InternationalJournalofElectricalPower&EnergySystems, 2014, 63: 105-112. DOI:10.1016/j.ijepes.2014.05.027.

Probabilistic load flow with non-Gaussian correlated input variables based on Gaussian mixture model

Huang Yu1Xu Qingshan1Liu Jiankun2Wei Peng2

(1School of Electrical Engineering, Southeast University, Nanjing 210096, China)(2Jiangsu Electric Power Research Institute, Nanjing 210003, China)

An algorithm for probabilistic load flow considering the correlation between input variables was proposed. A Gaussian mixture model (GMM) was established by the algorithm to represent non-Gaussian input variables in the system. On such a basis, a Gaussian component combination method (GCCM) was introduced and the marginal distribution of any output variable was directly obtained from multiple weighted least square runs (WLS). A study was also carried out to reduce the number of trials by limiting the number of Gaussian components. The simulation and error analysis on IEEE-30 test system indicated that GMM had the features of high fitting precision and wide applicability. The results obtained from the proposed method are identical to that of MCS and the computational efficiency is obviously improved. The effectiveness and the accuracy are proved to be closely related to operation times of WLS.

Gaussian mixture model; reduction algorithm; correlation; Gaussian component combination; probabilistic load flow

10.3969/j.issn.1001-0505.2017.02.016

2016-07-19. 作者简介: 黄煜(1992—),男,博士生；徐青山(联系人),男,博士,教授,博士生导师,xuqingshan@seu.edu.cn.

国家自然科学基金资助项目(51577028)、国家电网公司科技资助项目.

黄煜,徐青山,刘建坤,等.基于混合高斯模型的相关非高斯输入变量随机潮流计算[J].东南大学学报(自然科学版),2017,47(2):291-298.

10.3969/j.issn.1001-0505.2017.02.016.

TM74

A

1001-0505(2017)02-0291-08