基于球元重建与大涡模拟耦合并行算法的数值模拟

郭飞宏 王泽宇 仲兆平 王肖祎

(1东南大学能源与环境学院, 南京 210096)(2东南大学建筑设计院有限公司, 南京 210096)

基于球元重建与大涡模拟耦合并行算法的数值模拟

郭飞宏1王泽宇1仲兆平1王肖祎2

(1东南大学能源与环境学院, 南京 210096)(2东南大学建筑设计院有限公司, 南京 210096)

为了更好地模拟柱形颗粒与石英砂的流动,利用球元重建方法对柱形颗粒进行球元重建.采用大涡模拟中的SGS(sub-grid scale)亚格子模型,对柱形颗粒造成的湍流进行解析.模拟中耦合并行算法,缩短了模型计算时间.基于上述方法,模拟了表观气速为1.5 m/s的柱形颗粒与石英砂的混合流动过程. 通过流动瞬时图像和压力脉动分析表明,模拟结果与实验结果相似,表明耦合并行算法能较好地模拟流化床中柱形颗粒与石英砂的流动.当柱形颗粒尺寸较大时,加剧了湍流效应对混合流动的影响.模拟的z方向气体平均速度呈现中间高两边低的对称分布状态,这与床内的气泡和柱形颗粒分布有关,符合实际流化规律.

柱形颗粒;石英砂;模拟;球元重建;大涡模拟;并行算法

传统的离散元和计算流体力学方法(DEM-CFD)只能对球形颗粒的流动进行模拟,然而在实际的硫化床气固反应过程中,有很多柱形颗粒[1-3].柱形颗粒形状改变了颗粒与湍流的相互作用,不同形状颗粒在流场中的碰撞和受力有显著的差异[4-5].在研究方法上,缺少对柱形颗粒系统的实验研究,针对球形颗粒的研究方法应用于柱形颗粒系统时,容易产生很大的误差.对流态化下柱形颗粒的运动开展数值模拟也具有一定的难度,如何构建柱形颗粒,采用较为统一的数理模型描述柱形颗粒的受力和运动,是至今仍未完全解决的难题.国内外很多研究者对DEM-CFD方法进行了改进,Hilton等[6]采用超曲面法建立非球形颗粒模型,模拟了非球形颗粒在流化床中的流动.Zhong等[7]对气固流化床中的柱形颗粒流动进行了模拟,将柱形颗粒抽象为球元的组合体.Ren等[8-9]对流化床中玉米状颗粒流动进行了模拟,与Zhong等[7]的方法一样,仍然是将非球形颗粒抽象为球元的结合体,颗粒所受气相曳力近似等于球元所受曳力之和.卢洲等[10]采用DEM-CFD方法模拟了弯管中输送过程的柱状颗粒.Oschmann等[11]采用球元聚集法和多面体法构造柱形颗粒并描述颗粒之间的运动.当颗粒尺寸较大时,无法忽视流化床湍流对气固流动的影响.大涡数值模拟对于尺寸大于网格的湍流,采用直接数值求解[12-14];对于尺寸小于网格的小尺度的湍流脉动,采用SGS模型求解.由于大涡模拟能在较短的计算时间内获得比雷诺平均模拟更多更准确的湍流信息.因此,大涡模拟在湍流解析上得到愈来愈广泛的运用.

本文采用球元重建方法,将柱形颗粒表面所受的曳力转化为虚拟球元所受的曳力.采用大涡模型,并引入并行算法,从而实现柱形颗粒与石英砂流动的DEM-CFD并行模拟.

1 基本理论

1.1 球元重建

计算CFD气固曳力时,采用直径为0.8 mm虚拟球元重建一个长10 mm、直径10 mm的柱形颗粒模拟真实柱形颗粒(见图1).本文采用0.8 mm的虚拟球元,一方面虚拟球元的直径与石英砂颗粒直径大小相同,利于计算;另一方面,球元之间成正四面体紧密堆积,此时网格的空隙率约为0.2.当CFD计算网格完全处于柱形颗粒内部时,既能保证计算过程有很好的收敛性,又能借助虚拟球元实现在柱形颗粒内部对流体形成较大的阻力,使得柱形颗粒内部流体速度接近于零.在计算柱形颗粒与其他颗粒及壁面碰撞时,由直径为1.5 mm的虚拟球元重建形成一个中空的柱形壳体,如图1(c)所示.选用1.5 mm的虚拟球元有利于计算,同时保证了柱形颗粒重构的准确性.采用壳体布置方式的原因是:DEM计算过程中,计算颗粒碰撞力所用的时间很长,且计算用时随着颗粒数量的增加呈指数级增加.研究发现,在双组分DEM-CFD模拟中,可以忽略柱形颗粒内部球元的受力状况,这样可以缩短计算时间.为了尽可能地接近柱形颗粒的表面,球元与球元之间存在重叠.

(a) 柱形颗粒

(b) CFD球元重建

(c) DEM球元重建

为了验证球元重建的有效性,对柱形颗粒曳力系数Cd进行定量分析.通过改变虚拟球元大小,进而改变柱形颗粒内部的空隙率,模拟柱形颗粒曳力系数随雷诺数的变化.如图2所示,柱形颗粒曳力系数Cd随着雷诺数的增加而逐渐减小,并且最后趋于稳定;柱形颗粒曳力系数Cd随着虚拟球元所占体积分数a的增加而增加.当Re<3 000,α=0.7时,曳力系数与实验曲线吻合良好；而当Re>3 000,α=0.7时,曳力系数与实验值有轻微偏离,而α=0.5时，与实验曲线吻合良好.本次模拟的截面气速在1.0～2.0 m/s之间,因此对应的雷诺数一般小于3 000,所以控制虚拟球元大小使α=0.7,可以获得较好的流动模拟结果.

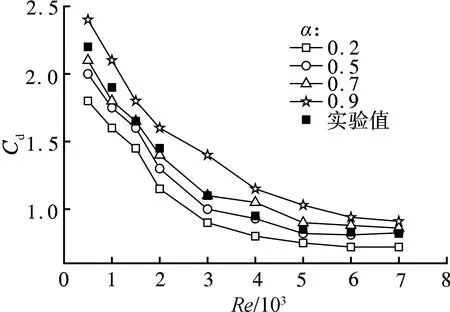
图2 柱形颗粒曳力系数Cd随雷诺数Re的变化

1.2 大涡模拟

对于湍流的解析,采用大涡模型中普遍采用的SGS(sub-grid scale)亚格子模型[15].在对传统N-S方程进行过滤后,大涡模型的连续性方程和动量方程为

(1)

-ε

(2)

(3)

(4)

(5)

式中,Cs为SGS常数,在本次模拟研究中取0.13;Δ为特征长度,根据孔隙率的不同,其表达式为

(6)

1.3 气固作用力

(7)

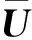
(8)

本研究中,根据空隙率的不同分别采用Ergun和en&Yu模型来表示气固曳力系数β,表达式为

(9)

式中,Cd为流场内的颗粒曳力系数,由Shiller和Naumann方程以及牛顿曳力法则计算,即

(10)

式中, 雷诺数Re的表达式为

(11)

(12)

式中,αp和αc分别为单个计算网格内石英砂和生物质的体积分数;αfic为生物质内虚拟颗粒的体积分数;dp和dfic为石英砂颗粒和虚拟颗粒的直径.

1.4 离散元方法

Tsuji等[5]提出了DEM-CFD方法,将DEM模型引入到稠密气固两相流动的模拟研究中.其基本思想是假设颗粒在碰撞过程中可以有轻微的重叠现象并可以持续一定的时间.如图3所示,采用弹簧、阻尼器和滑移器来表示颗粒与颗粒间或颗粒与壁面间的碰撞.

(a) 法线方向 (b) 切线方向

1—弹簧；2—滑移器；3—阻尼器

图3 DEM颗粒碰撞示意图

颗粒发生碰撞时其作用力在碰撞点上,这个力称为颗粒接触力Fc.颗粒接触力被分为法向力Fcn和切向力Fct,法向力使颗粒发生平动,切向力由于作用方向线与指点不在同一直线上,会产生力矩使颗粒发生转动.法向力Fcn和切向力Fct由下式计算：

Fcn=-kndn-ηnvn

(13)

vn=(vr·n)n

(14)

Fct=-ktdt-ηtvt

(15)

vt=vr-(vr·n)n+rwp×n

(16)

式中,dn和dt分别表示法向和切向的相对位移;vr为颗粒间相对速度;vt表示碰撞点的相对滑移速度;kn和kt分别表示法向和切向方向弹簧的弹性系数;ηn和ηt分别为法向和切向的阻尼系数;n为单位法向量;wp为颗粒间相对角速度.阻尼系数η可由恢复系数e确定,即

(17)

(18)

α=-(1/π)lne

(19)

式中，m为质量；k为弹性系数.在计算柱形颗粒接触力时,只需计算柱形颗粒表面的球元与其他颗粒或壁面的碰撞,柱形颗粒表面球元碰撞接触力计算方法与球形颗粒是相同的.在柱形颗粒与其他颗粒碰撞时,可能只有一个球元受力,也可能有多个球元同时受力.球形颗粒与柱形颗粒的碰撞视为球形颗粒与球元的碰撞.柱形颗粒总的受力为柱形颗粒内所有球元的受力.柱形颗粒的运动可以认为是由球元的平动和转动叠加产生的.根据牛顿第二定律,球形颗粒i的平动和转动方程为

(20)

(21)

式中,mp为颗粒质量;vpi为颗粒i的速度矢量;fpi为颗粒i所受气相曳力;∑Fci为颗粒i所受接触力总和;Ip为颗粒的转动惯量;ωpi为颗粒i的角速度矢量;∑Mpi为颗粒i所受力矩总和.

1.5 并行算法

对柱形颗粒与石英砂流动进行模拟,采用了区域分解技术和颗粒分配技术相结合的方法[16-17].基于信息传递的并行编程技术(message passing interface,MPI)对CFD求解区域和颗粒碰撞计算进行多线程并行算法优化.在CFD计算中,连续相的速度、压力等重要参数需要耦合迭代计算,一个时间步长需要进行上千次的迭代计算,因此连续相的速度、压力的计算是一个十分复杂且耗时的过程,对整个计算区域按照x方向进行区域划分.程序运行后,在同一时刻存在N个线程对不同计算区域进行CFD求解,这样单位时间内进行的迭代次数就会明显增加.而每个计算域都比原先划分多了左右2列虚拟边界作为数据缓冲区,这些区域存储了与当前计算域相邻的边界信息.在一个迭代计算步骤中,分区的边界信息通过通信句柄MPI_send将计算域的边界信息传输至虚拟边界,通过通信句柄MPI_recv从相邻区域的缓冲区获取边界信息以保证整个流场迭代计算的连续性.在DEM计算中,由于颗粒数量较多,通常都有几十万个,因此颗粒碰撞力占用了绝大部分的DEM计算时间,需要对这部分计算进行并行算法优化.系统统一对柱形颗粒中的虚拟球元和石英砂颗粒分配ID号,然后按照ID号的大小将不同颗粒的计算任务分配给不同的线程处理,从而提高计算效率.

2 模型的建立

2.1 基本流程图

本文模拟的计算流程如图4所示,采用Fortran语言编写程序.在一个时间步长内,模拟程序主要进行了两大部分计算：① 连续相求解(CFD).基于正交结构化交错网格和有限体积离散方法求解连续相的流场.将动量方程离散后采用SIMPLE算法进行计算.首先假设一个压力场已知,求解流场的速度,然后修正压力和速度,最后进行迭代计算判断收敛性.② 离散相求解(DEM).首先检索网格内的颗粒,判断颗粒是柱形颗粒中的球元颗粒还是石英砂颗粒.采用颗粒碰撞软球模型和球元重建理论,计算颗粒间的碰撞力,得到柱形颗粒(虚拟球元)和石英砂的运动轨迹.

图4 DEM-CFD模拟计算流程

2.2 计算区域及定解条件

构建80 mm×40 mm×500 mm的计算区域.如果网格尺寸过大,会使模拟计算精度大大降低;如果网格尺寸过小,则气固曳力公式不适用.在CFD计算中,网格尺寸一般为颗粒尺寸的2.5～4.0倍.在DEM计算中,网格尺寸的要求相对较低,一般为颗粒尺寸的1.0～1.5倍.模拟的计算区域与实验中的流化床几何尺寸一致,在实验中观察到流化床上半部分几乎没有颗粒的存在,为节省模拟时间,在模拟中只计算床内高度小于500 mm的流动情况.流化床的几何尺寸见图5.流化床模拟计算中,壁面采用无滑移边界条件.入口边界采用速度入口边界条件,布风板上气孔内设置为速度入口边界条件,其余部分为壁面的无滑移边界条件.出口边界采用常用的压力出口边界条件.对于冷态模拟,床内压强和气相速度的初始条件对模拟结果的影响很小,本研究设置初始压强为0,初始气相速度为0.

(a) 主视图

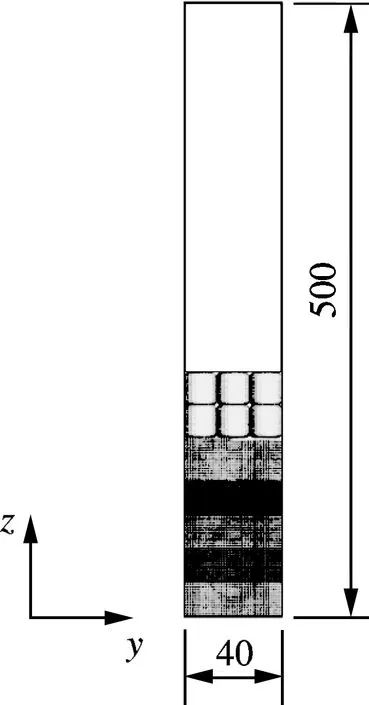
(b) 侧视图

2.3 基本参数

流化床柱形颗粒-石英砂双组分流动模拟主要参数见表1.

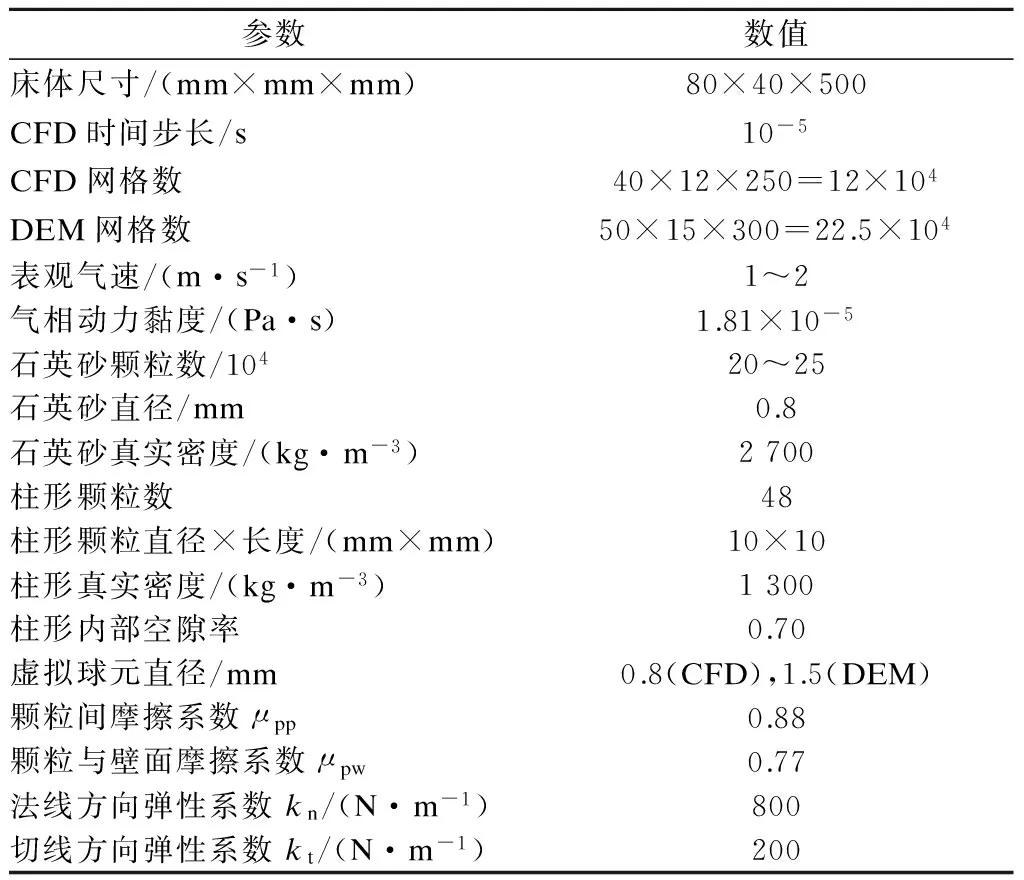
表1 柱形颗粒-石英砂双组分流动模拟参数

3 结果与讨论

3.1 流动图像分析

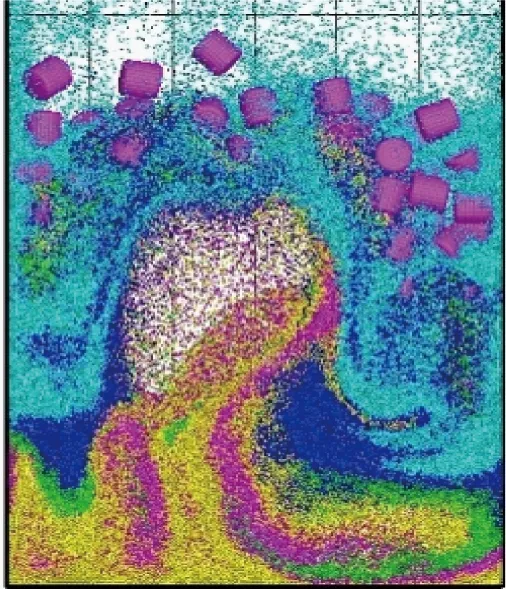
模拟结果采用Tecplot360图像后处理软件输出.图6为柱形颗粒质量分数为10%、表观气速为1.5 m/s时,柱形颗粒与石英砂混合流动模拟图.图7为该工况下的流动瞬时图.对比模拟图和流动瞬时图可以发现,模拟结果与实验结果得到的图像较为相似.当t=0 s时,柱形颗粒分布在石英砂上面,流化床处于静止状态,床高约为60 mm.随着时间的增加,颗粒开始流化:当t=0.3 s时,床层下部形成比较明显的大气泡,柱形颗粒和石英砂在气泡的作用下被吹起,床层“膨胀”的高度为150 mm左右,约为静止床高的2.5倍,此时柱形颗粒主要集中在石英砂上部,虽然被气泡带到一定高度,但与石英砂并未较好地混合.当t=0.5 s时,气泡逐渐增大和上升,在床层中部形成较大的气泡区间,此时柱形颗粒已经到达一定的高度,最大位置变化不大,但是由于中间气泡的上升,部分石英砂和柱形颗粒受到中间力的作用,开始向床两侧的壁面移动.当t=1.2 s时,气泡破裂成较小气泡,柱形颗粒和石英砂回落,并再次与上升的气泡相聚,造成气泡重复破裂(见图6),整个过程有利于柱形颗粒和石英砂的混合.在0～1.2 s的过程中,气泡的形成—生长—破裂、柱形颗粒的上升和下落、柱形颗粒与石英砂的混合程度在逐渐增加.且图6的气固流动行为与图7中实验拍摄的图像行为十分相似,模拟效果较好.

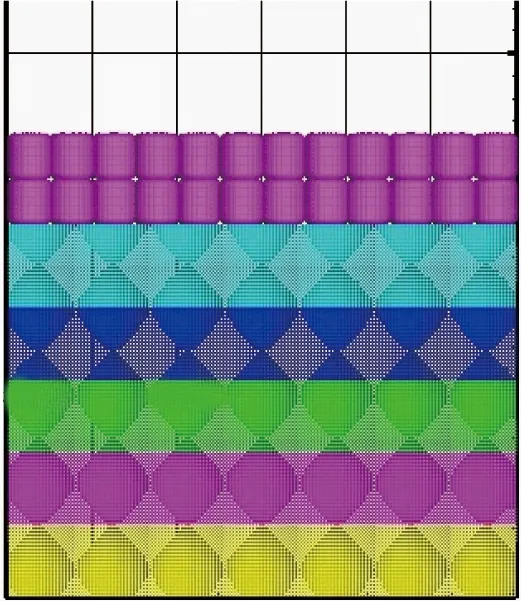
(a) t=0 s

(b) t=0.3 s

(c) t=0.5 s

(d) t=1.2 s

(a) t=0 s

(b) t=0.3 s

(c) t=0.5 s

(d) t=1.2 s

当t=1.0 s时,柱形颗粒与石英砂的流动与模拟如图8所示.此时,较大柱形颗粒的回落会对区域A内的大气泡造成破裂,形成较小气泡.回落的颗粒再次与上升的气泡相聚,造成气泡重复破裂,促进柱形颗粒和石英砂的混合.图8中的流动图像和模拟图像均较好地反映出了这一现象.同时,由于柱形颗粒体积较大,四周的石英砂与其碰撞后容易向外侧运动,在柱形颗粒周围形成较大空隙.这样,在计算气固曳力时就需要考虑湍流对气固流动的影响.

(a) 模拟图 (b) 流动图

3.2 压力脉动分析

图9为不同床层高度h的压降模拟值与实验值对比.由于最小流化速度为0.5 m/s,因此模拟没有包含固定床工况(表观气速v<0.5 m/s).当床高h=50 mm时,实验值的床层压降随着气速的增加,先上升后下降并趋于稳定,流化后的平均压降ΔP为1.3 kPa.模拟值主要处于流化阶段,床层平均压降约为1.2 kPa.当床高h=85 mm时,压降

(a) h=50 mm

(b) h=85 mm

随着气速的增加,先上升后下降并趋于稳定,流化后的平均压降约为1.7 kPa,模拟的平均压降约为1.6 kPa.由于在模拟过程中布风条件、床料形状和尺寸等方面做了一系列简化假设,因而模拟结果与实验结果存在一定的偏差,相同气速条件下床层压差的偏差量在10%以内.当表观气速大于临界流化风速时,模拟方法能较为准确地模拟分析真实柱形颗粒与石英砂混合流动时的压力脉动.

3.3 湍流分析

在传统的流化床中,气速分布均匀,雷诺数比较小,湍流对气固流动的影响不很明显.但是在柱形颗粒和石英砂的混合流动过程中,柱形颗粒尺寸比较大,加剧了湍流效应对流动的影响,因此有必要对湍流进行分析.大涡模拟的基本思想是对大尺度湍流用直接数值模拟方法求解,对小尺度湍流在添加亚格子尺度应力后,采用SGS模型求解.小尺度湍流对大尺度湍流的影响主要表现在耗散效应上,也就是说大涡模拟中的能量耗散是从大涡向小涡串级传输的形式出现.SGS湍流黏度的大小在一定程度上反映了小涡对大涡的影响.利用SGS湍流黏度来定量分析柱形颗粒对气体湍流耗散产生的影响.图10为不同气速下SGS湍流黏度的分布.图中红色为较大的湍流黏度,蓝色为较小的湍流黏度,颜色越深对应的SGS湍流黏度越大.由于喷口附近进气速度较大,雷诺数较高,在喷口上方很小区域会形成湍流黏度最大的区域.当表观气速v=1.0 m/s时,气体速度较低,床内柱形颗粒和石英砂的流动不很充分.此时,气体呈气拴式由床层底部向上缓慢运动,颗粒上下混合不均匀.柱形颗粒聚集在石英砂上部,气体穿过此区域后在颗粒层上部形成了较强的尾涡,从而增加了气体的黏性耗散,SGS湍流黏度较大.当表观气速v=1.5 m/s时,流化床内产生的气泡变大,混合流动加剧,柱形颗粒和石英砂混合较为充分,颗粒在整个床层内分布较为分散,此时SGS湍流黏度分布相对于表观气速v=1.0 m/s时较为均匀.

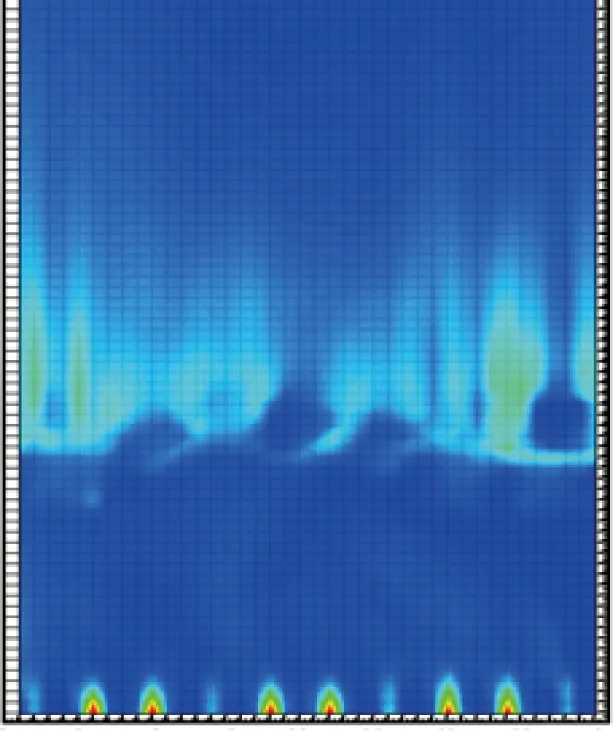
(a) v=1.0 m/s

(b) v=1.5 m/s

3.4 气相速度

图11为不同表观气速下,不同床层高度z方向气体平均速度vz的分布.流化床x方向的长度为80 mm.当表观气速v=1.0 m/s时,低床层(h=20,40 mm)z方向气体平均速度受喷口进气影响较大,此时的气相速度范围为1.4～1.8 m/s,平均速度分别为1.6和1.5 m/s.当h=80 mm时,z方向气体平均速度明显下降,呈现中间低两边高的波动分布状态,说明气体穿过底部床料层后向壁面偏移,并沿着壁面向上运动.这主要是由于柱形颗粒的布置和表观气速较低造成的.如图7(a)所示,柱形颗粒开始集中在x方向中心位置,颗粒本身的重力会对底部中心造成附加压力,这种附加的阻力导致气体向压力较低的两侧壁面运动.当表观气速较小(1.0 m/s)时,气体呈气拴式由床层底部向上缓慢运动,颗粒上下混合不均匀,这种附加压力会持续一段时间.z方向气体平均速度的波动分布还与布风板的设计有关.

(a) v=1.0 m/s

(b) v=1.5 m/s

当表观气速v=1.5 m/s时,床内z方向气体平均速度呈现中间高两边低的对称分布状态.当床层高度从40 mm增加到200 mm时,z方向气体最大速度分别从3.0 m/s下降到1.5 m/s;当h=40,80 mm时,中间区域气体纵向速度是左、右两侧靠近壁面处的2倍.这是由于在中间床层产生了较大的气泡(见图7(b)),床料颗粒受到气泡的抬升和排挤作用向两侧回落,因此气体在中间受到床料的阻力比靠近壁面要小,造成了气体平均速度呈现中间高两边低的对称分布状态.表观气速增加后,h=20 mm的低床层同时受到喷口进气和气固混合的影响.当表观气速为1.5 m/s时,z方向气体平均速度波动性明显加大,靠近壁面x=70～80 mm位置处,气相速度较低.这主要是因为表观气速的增加,加剧了柱形颗粒与石英砂的混合,而这种混合并不均匀.运动过程中受到多种因素的影响,柱形颗粒和石英砂的分布不均匀,体现在z方向气体平均速度的波动(见图7(d)).当h=200 mm时气体已经穿过床料层,纵向速度分布较为均匀,接近表观气速1.5 m/s.

4 结论

1) 采用球元重建方法,构建了柱形颗粒,利用大涡模拟中的SGS亚格子模型,对湍流进行解析,同时耦合并行算法,缩短了计算时间.

2) 基于球元重建与大涡模拟耦合并行算法对柱形颗粒和石英砂的混合流动进行了模拟,模拟结果与实验结果相似.

3) 模拟结果表明:较大柱形颗粒的上升和回落会造成气泡的破裂,促进柱形颗粒和石英砂的混合;柱形颗粒尺寸较大,加剧了湍流效应对流动的影响,有必要对湍流进行解析;当表观气速v=1.5 m/s时,床内z方向气体平均速度呈现中间高两边低的对称分布状态,这主要与床内的气泡和柱形颗粒分布有关,符合实际流化规律.

References)

[1]Khan A A, de Jong W, Jansens P J, et al. Biomass combustion in fluidized bed boilers: Potential problems and remedies[J].FuelProcessingTechnology, 2009, 90(1): 21-50. DOI: 10.1016/j.fuproc.2008.07.012.

[2]Cheng H, Hu Y. Municipal solid waste (MSW) as a renewable source of energy: Current and future practices in China[J].BioresourceTechnology, 2010, 101(11): 3816-3824. DOI:10.1016/j.biortech.2010.01.040.

[3]Hilton J E, Cleary P W. The influence of particle shape on flow modes in pneumatic conveying[J].ChemicalEngineeringScience, 2011, 66(3): 231-240. DOI:10.1016/j.ces.2010.09.034.

[4]Wang C, Zhong Z, Wang X. Microscopic flow characteristics in fluidized bed of cylinder-shaped particles[J].KoreanJournalofChemicalEngineering, 2015, 32(12): 2384-2393. DOI:10.1007/s11814-015-0033-y.

[5]Tsuji T, Higashida K, Okuyama Y, et al. Fictitious particle method: A numerical model for flows including dense solids with large size difference[J].AIChEJournal, 2014, 60(5): 1606-1620. DOI:10.1002/aic.14355.

[6]Hilton J E, Mason L R, Cleary P W. Dynamics of gas-solid fluidised beds with non-spherical particle geometry[J].ChemicalEngineeringScience, 2010, 65(5): 1584-1596. DOI:10.1016/j.ces.2009.10.028.

[7]Zhong W Q, Zhang Y, Jin B S, et al. Discrete element method simulation of cylinder-shaped particle flow in a gas-solid fluidized bed[J].ChemicalEngineering&Technology, 2009, 32(3): 386-391. DOI: 10.1002/ceat.200800516.

[8]Ren B, Zhong W, Chen Y, et al. CFD-DEM simulation of spouting of corn-shaped particles[J].Particuology, 2012, 10(5): 562-572. DOI:10.1016/j.partic.2012.03.011.

[9]Ren B, Zhong W, Jiang X, et al. Numerical simulation of spouting of cylindroid particles in a spouted bed[J].TheCanadianJournalofChemicalEngineering, 2014, 92(5): 928-934. DOI:10.1002/cjce.21900.

[10]卢洲,刘雪东,潘兵.基于CFD-DEM方法的柱状颗粒在弯管中输送过程的数值模拟[J].中国粉体技术,2011,17(5):65-69.DOI:10.3969/j.issn.1008-5548.2011.05.017. Lu Zhou, Liu Xuedong, Pan Bing. Numerical simulation of the process of cylindrical particles in elbow pipe based on CFD-DEM method [J].ChinaPowderTechnology, 2011, 17(5): 65-69. DOI:10.3969/j.issn.1008-5548.2011.05.017. (in Chinese)

[11]Oschmann T, Hold J, Kruggel-Emden H. Numerical investigation of mixing and orientation of non-spherical particles in a model type fluidized bed[J].PowderTechnology, 2014, 258: 304-323. DOI: 10.1016/j.powtec.2014.03.046.

[12]Yamamoto Y, PotthoffM, Tanaka T, et al. Large-eddy simulation of turbulent gas-particle flow in a vertical channel: Effect of considering inter-particle collisions[J].JournalofFluidMechanics, 2001, 442: 303-334.DOI:10.1017/s0022112001005092.

[13]Koukouvinis P, Gavaises M, Li J, et al. Large eddy simulation of diesel injector including cavitation effects and correlation to erosion damage[J].Fuel, 2016, 175: 26-39. DOI: 10.1016/j.fuel.2016.02.037.

[14]Yin B, Yu S, Jia H, et al. Numerical research of diesel spray and atomization coupled cavitation by large eddy simulation (LES) under high injection pressure[J].InternationalJournalofHeatandFluidFlow, 2016, 59: 1-9. DOI: 10.1016/j.ijheatfluidflow.2016.01.005.

[15]Hoover K A, Foley M G, Heasler P G, et al. Sub-grid-scale characterization of channel lengths for use in catchment modeling[J].WaterResourcesResearch, 1991, 27(11): 2865-2873. DOI: 10.1029/91WR01551.

[16]Li T, Garg R, Galvin J, et al. Open-source MFIX-DEM software for gas-solids flows: Part Ⅱ—Validation studies[J].PowderTechnology, 2012, 220(SI): 138-150. DOI: 10.1016/j.powtec.2011.09.020.

[17]Garg R, Galvin J, Li T, et al. Open-source MFIX-DEM software for gas-solids flows: Part Ⅰ—Verification studies[J].PowderTechnology, 2012, 220(SI): 122-137. DOI: 10.1016/j.powtec.2011.09.019.

Numerical simulation based on sphere reconstruction and large eddy simulation coupled parallel algorithm

Guo Feihong1Wang Zeyu1Zhong Zhaoping1Wang Xiaoyi2

(1School of Energy and Environment, Southeast University, Nanjing 210096, China)(2Architectural Design and Research Institute Co., Ltd., Southeast University, Nanjing 210096, China)

To simulate the mixing flow of cylindrical particles and quartz sand, the spherical element was used to reconstruct cylindrical particles. A sub-grid scale (SGS) model was used to analyze the turbulent flow. The coupled parallel algorithm in simulation reduced the computation time. Based on the above method, the mixing flow process of cylindrical particles and the quartz sand at 1.5 m/s was simulated. The simulation results were in good agreement with the experimental results on instantaneous flow and pressure fluctuation. The result shows that the proposed method can simulate the mixing flow of cylindrical particles and the quartz sand in fluidized bed. When the size of cylindrical particles is larger, the influence of the turbulence on mixing flow is aggravated. The average velocity of gas in thezdirection is simulated, presenting symmetrical distribution of high in the middle and low on both sides. This is related to the distribution of bubbles and cylindrical particles in fluidized bed, thus it is in line with the actual fluidization law.

cylindrical particles; quarts sand; simulation; spherical element reconstruction; large eddy simulation; parallel algorithm

10.3969/j.issn.1001-0505.2017.02.015

2016-07-25. 作者简介: 郭飞宏(1986—)，男，博士生；仲兆平(联系人)，男，博士，教授，博士生导师，zzhong@seu.edu.cn.

国家自然科学基金资助项目(U13161115,51276040)、东南大学优秀博士学位论文培育基金资助项目(YBJJ1644).

郭飞宏,王泽宇,仲兆平,等.基于球元重建与大涡模拟耦合并行算法的数值模拟[J].东南大学学报(自然科学版),2017,47(2):283-290.

10.3969/j.issn.1001-0505.2017.02.015.

TQ051

A

1001-0505(2017)02-0283-08