改进各向异性扩散模型在图像滤波去噪中的应用*
张长胜, 冯 广, 刘子裕, 李 川, 钱 斌
(1.昆明理工大学 信息工程与自动化学院,云南 昆明 650500;2.中国能源建设集团云南省电力设计院有限公司,云南 昆明 650051)
应用技术
改进各向异性扩散模型在图像滤波去噪中的应用*
张长胜1, 冯 广1, 刘子裕2, 李 川1, 钱 斌1
(1.昆明理工大学 信息工程与自动化学院,云南 昆明 650500;2.中国能源建设集团云南省电力设计院有限公司,云南 昆明 650051)
为了增强锅炉水位计图像滤波去噪效果,提高图像清晰度,便于后期液位计图像识别研究,通过分析P-M各向异性扩散模型、选择扩散模型及You Yu-Li和Kaveh M四阶偏微分方程的滤波去噪算法,提出了改进各向异性扩散模型滤波算法。所提算法对Perona和Malik两个扩散函数均值化,并引入标准差作为梯度期望值的偏差裕度,结合了P-M各向异性扩散模型保边缘特性的优点,并消除了由于传统各向异性滤波算法迭代过度所造成的阶梯缺陷问题,确保图像有用信息不缺失和像素点平滑度。实验结果表明:所提算法能够更好地降低噪声对目标信号提取产生的影响,提高了图像识别鲁棒性,增强了图像平滑滤波效果,保证了锅炉水位计图像边缘清晰度和完整性。
滤波去噪; 液位计图像识别; 改进各向异性扩散模型算法; 边缘特性
0 引 言
锅炉作为一种特种压力容器,其可靠运行是安全生产的前提基础,因而需对其工况参数实时监测,其中汽包液位是最重要的参数之一。常规利用差压变送器与运行人员视觉观测玻璃管水位计结合的方式监控液位值,但该模式带有主观性,且工作强度大、效率低,故研发一种代替传统人工方式读取水位计液位值的智能遥视系统具有必要性。而锅炉水位计图像滤波去噪是智能遥视系统处理过程中的重要步骤,其保证了图像边缘信息的完整性,对后期图像特征提取和刻度识别精确度起着至关重要的作用。传统P-M各向异性扩散滤波算法被广泛应用于图像滤波、图像增强等[1,2],其虽保证了图像边缘一定的清晰度,但因过度迭代、噪声梯度等问题造成噪声同质区域滤波不彻底,图像有用信息缺失,像素点不能被平滑,图像平面出现起伏的情况,影响滤波效果[3]。因而,寻求一种好的图像滤波去噪算法对锅炉水位计图像去噪具有极其重要价值。
沈千里等人针对传统平滑模型去噪时带来的图像模糊及纹理失真等缺点,提出了自适应加权向量滤波法,该法尽可能使像素点与原图像保持一致,较彻底地滤除噪声且较好保护了图像纹理特征等信息,提高了人脸图像去噪效果[4]。黄一鹏针对硬、软阈值小波去噪算法存在不连续性和偏差的问题,提出新的阈值函数,其通过调节参数来调节阈值降低小波系数与原始小波系数之间的恒定偏差和过渡区内曲线平滑性,结果表明,改进小波阈值函数能获得较小均方误差,且去噪图像主观视觉效果和峰值信噪比均比传统算法优越[5]。杨学志等人结合区域滤波和双边滤波优点提出了一种基于边缘结构保持的图像高斯噪声抑制新算法,实验表明,该算法滤波效果较好[6]。任文琦等人利用四阶偏微分方程对各向异性扩散进行改进,并引入卷积场模型,实验表明,改进算法不仅滤波效果优于原始算法,且能够完整保留图像边缘信息[7]。
本文针对锅炉水位计图像识别,结合几类各向异性扩散滤波模型,提出了一种改进各向异性扩散的图像滤波去噪算法,比传统的各向异性扩散算法更加有效,图像滤波去噪效果明显提高,对于液位值自动读取具有重要意义。
1 P-M各向异性扩散模型
设待处理图像为I(x,y,t),定义区域Ω∈R×R是扩散初始区域,经各向异性扩散模型算法从内往外拓展扩散,即获得平滑图像I*(x,y,t)。各向异性扩散函数如下
(1)
Perona和Malik依据传统模型提出两个扩散函数,即P-M各向异性扩散模型
(2)

由P-M各向异性扩散模型方程绘制出当扩散门限分别为20和40时的曲线。如图1所示。
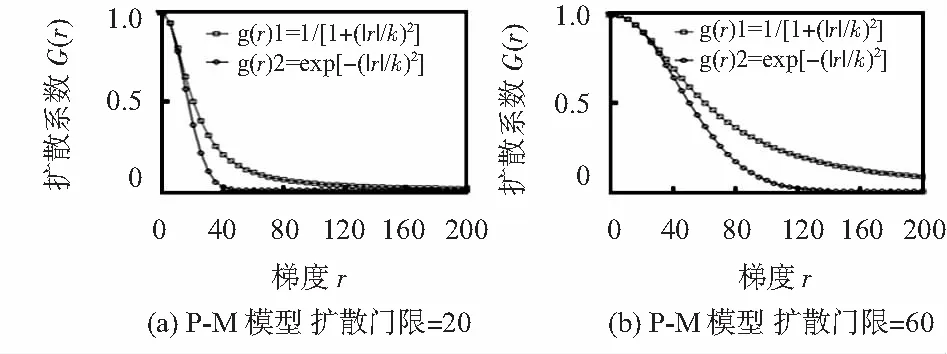
图1 不同扩散门限时P-M扩散模型曲线
根据图1可知扩散函数为非负减函数,扩散系数曲线与梯度值成反比,其特性表明扩散函数在图像低梯度区域的平滑滤波效果优于高梯度区域,起到了保图像边缘信息。但该扩散系数仅能在0和1之间波动,系数逐渐趋近于0,总是大于0,故在边缘区域像素时扩散迭代应及时结束,需人为设定迭代次数以便控制迭代扩散,否则将出现过度扩散,影响图像边缘信息。但在实际平滑过程中,该函数是不稳定的,人工方式估测迭代次数容易发生过度平滑或者欠平滑现象[10]。
2 其他改进各向异性扩散滤波
1)选择扩散模型:即F.Catté针对传统P-M各向异性扩散模型存在的问题提出了一种改进各向异性扩散模型,该模型将待处理图像高斯滤波,计算P-M各向异性扩散模型的扩散系数,达到降低噪声梯度值的目的。改进各向异性扩散模型为
(3)
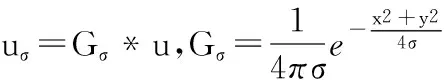
2)P-M各向异性扩散模型缺陷是平滑时噪声同质区扩散速度快于边缘区域,致使噪声区域被过度平滑,出现阶梯效应。P-M各向异性扩散模型的能量泛函数为
(4)

为避免阶梯效应,YouYu-Li和KavehM提出了四阶偏微分方程
(5)
该四阶偏微分方程的能量泛函数为
(6)
根据凹凸函数性质,当f为凹函数,满足f″(s)≥0,即在s≥0时取极小值,对应图像梯度最小值区域,故经迭代得到平滑图像;当f为凸函数,经迭代后全局最小值点出现在图像梯度值较大处,则图像的平滑区域拓展到余下块状区域,消除了传统P-M模型产生的阶梯效应。但该改进模型的不足之处是若图像存在单独较大噪声点,则像素点不能被平滑,造成图像平面出现起伏[12]。
3 改进各向异性扩散滤波
P-M各向异性扩散滤波算法优点是其很好地保留图像边缘信息,克服了传统算法在平滑过程中将边缘模糊的缺点,但算法同样存在不完全性,若遭遇强噪声,而扩散门限K不易控制,扩散处理后的图像将出现显著阶梯效应[13~15]。提出一种新的扩散函数
(7)
其中
(8)
改进后,扩散函数曲线如图2所示:设t1=15,t2=40,在梯度小于15的区间内,扩散系数为1;在限定区间(t1,t2)内,扩散系数满足式(7)且呈单调递减;当梯度大于40时,扩散函数被强制置0。
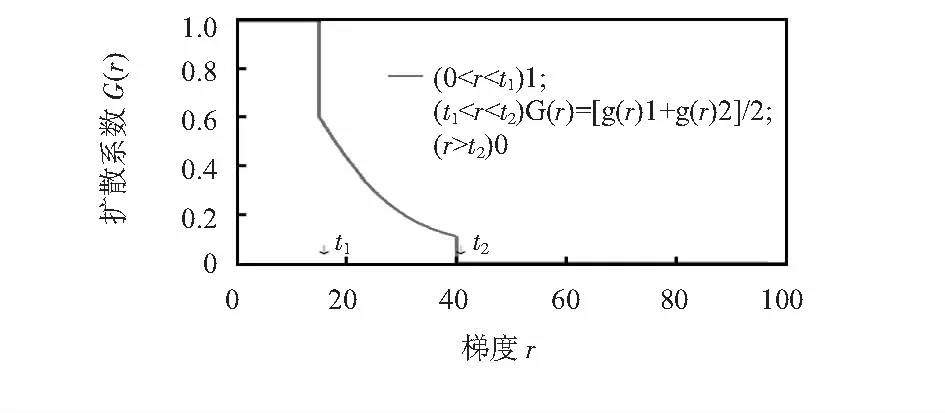
图2 改进各向异性扩散模型曲线
若t1和t2只是通过人为经验取值,那么主观因素将使扩散过程达不到所需效果,故本文给出了一种方法对两个设定值进行计算。如图3所示,将图像中像素点看成如下3×3领域。其梯度幅值定义为
(9)
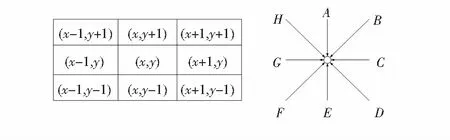
图3 像素点领域梯度计算原理图
其中
(10)
梯度幅值均值定义
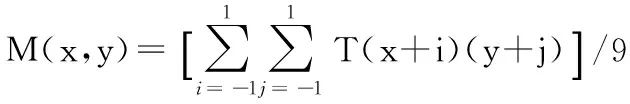
(11)
梯度幅值标准差定义为
(12)
由于考虑实际偏差影响,引入标准差σ(x,y)作为梯度期望值的偏差裕度,从而定义t1和t2为
(13)
(14)
该改进模型因对传统P-M扩散模型的g(x)1和g(x)2函数求平均函数G(x),有效避免因扩散过度或效果不佳产生的图像滤波效果差的问题。
该改进算法优于传统P-M各向异性扩散模型算法的主要原因是其分段扩散区间的设定,图像在高梯度区间和低梯度区间都包含有用的纹理信息,有效避免有用信息因扩散而被滤掉,其不仅减少了不必要的迭代次数,而且使平滑梯度区间具有更快平滑速度,保证了图像边缘信息完整性。
4 实验结果分析
为了验证该改进算法滤波去噪效果,实验选取P-M各向异性扩散模型、选择扩散模型和所提改进各向异性扩散算法进行滤波效果及时间对比,实验对象选用锅炉水位计图像,实验对比结果如图4、图5和图6所示。

图4 滤波效果图
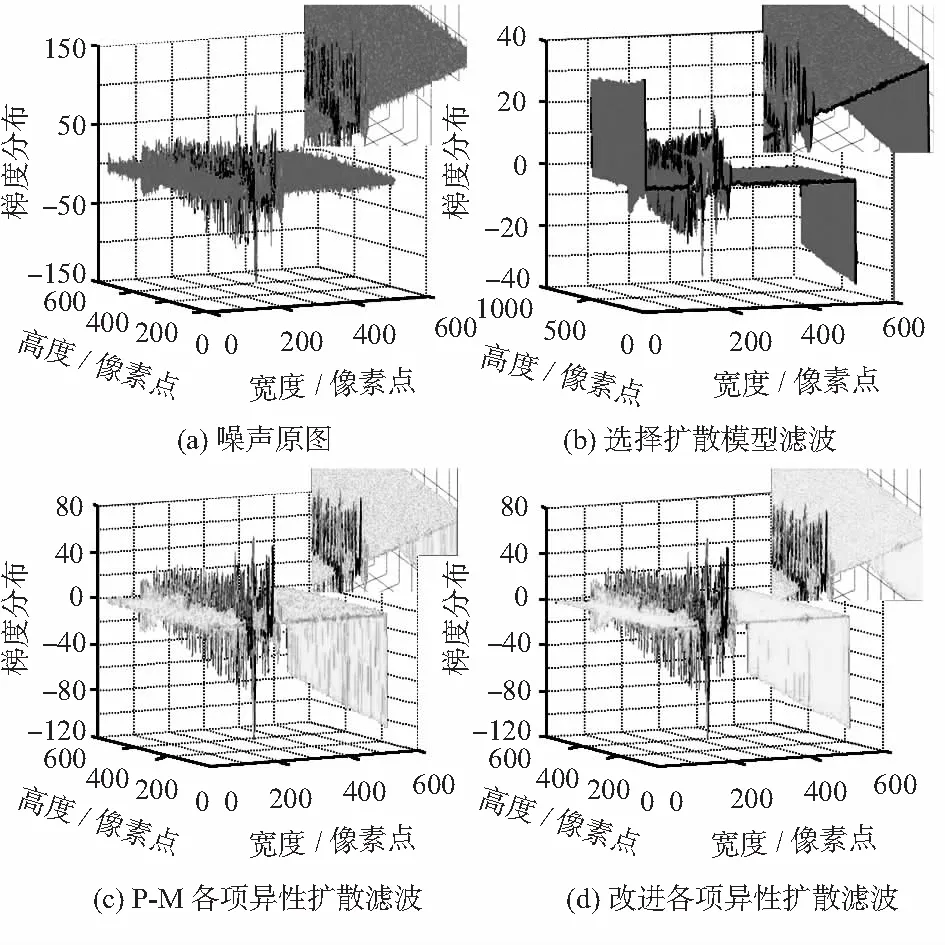
图5 图像梯度分布图
如图4所示,对比P-M各向异性扩散模型、选择扩散模型和改进各向异性扩散算法滤波效果图,改进各向异性扩散滤波算法滤波去噪效果较前两者更佳,图中噪点显著减少。图5为梯度分布对比,图(a)为原图梯度分布,其边缘最高梯度为60,而图(b)经扩散模型平滑后梯度值下降至15,使图像边缘模糊,图(c)和图(d)分别为P-M模型算法和改进各向异性扩散滤波算法,处理后图像边缘并未被过度平滑,且改进算法在噪声同质区域滤波效果优于传统算法,证明改进有效。如图6所示,3种滤波算法滤波时间对比,P-M滤波算法为170 ms,扩散模型为120 ms,改进滤波算法为140 ms,其中,改进算法滤波时间介于两种算法之间。

图6 滤波时间对比
滤波去噪峰值信噪比计算如下
(15)
式中 size为图像尺寸大小,I为输入图像,O为输出图像。
峰值信噪比(PSNR)越大则代表图像失真越少,如表1所示,改进后的扩散滤波PSNR较高,证明其去噪滤波效果最好。

表1 峰值PSNR对比
5 结束语
本文分析了P-M各向异性扩散滤波算法、选择扩散模型和You Yu-Li和Kaveh M的四阶偏微分方程,给出了一种改进的各向异性扩散模型的图像滤波去噪算法。通过实验结果可知:改进各向异性扩散模型滤波效果更佳,图像清晰度更高且有效降低了传统理论分析的复杂程度, 简化了扩散滤波方法,避免了传统P-M扩散模型的滤波效果不稳定性。
[1] Monteil J,Beghdadi A.A new interpretation of the nonlinear an-isotropic diffusion for image enhancement[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1999,21(9):940-946.
[2] Segall C A,Acton S T.Morphological anisotropic diffusion[C]∥Proceedings of the IEEE International Conference on Image Processing,Santa Barbara,CA,USA,1997:348-351.
[3] Catte F,Lions P I,Morel J,et al.Image selective smoothing and edge detection by nonlinear diffusion[J].SIAM Journal on Numerical Analysis,1992,29(1):182- 193.
[4] 沈千里,陈 晓,支亚京,等.一种新的人脸图像去噪算法[J].传感器与微系统,2015,34(11):133-136.
[5] 黄一鹏.一种基于新的小波阈值函数的图像去噪方法[J].传感器与微系统,2011,30(9):76-81.
[6] 杨学志,徐 勇,方 静,等.结合区域分割和双边滤波的图像去噪新算法[J].中国图像图形学报,2012,17(1):40-48.
[7] 任文琦,王元全.基于梯度矢量卷积场的四阶各向异性扩散及图像去噪[J].光学精密工程,2013,21(10):2713-2719.
[8] 赵 德,何传江,陈 强.结合局部熵的各向异性扩散模型[J].模式识别与人工智能,2012,25(4):642-647.
[9] 郑满满,胡小兵,郑申海.各向异性扩散图像去噪的改进模型[J].计算机工程与应用,2013,49(18):130-133.
[10] 赵海勇,贾仰理.一种改进的各向异性扩散去噪模型[J].计算机科学,2013,40(11A):147-149.
[11] 钱伟新,刘瑞根,王婉丽,等.基于图像特征方向的各向异性扩散滤波方法[J].中国图象图形学报,2006,11(6):818-822.
[12] 高 源,于晓洋.正则化最小二乘结合偏微分方程的图像复原技术研究[D].哈尔滨:哈尔滨理工大学,2010.
[13] 付丽娟,姚 宇,付忠良.中值滤波与各向异性扩散相结合的医学图像滤波方法[J].计算机应用,2014,34(1):145-148.
[14] 吴 俊,汪源源,陈 悦,等.基于同质区域自动选取的各向异性扩散超声图像去噪[J].光学精密工程,2014,22(5):1312-1321.
[15] 翟东海,鱼 江,段维夏,等.米字型各向异性扩散模型的图像去噪算法[J].计算机应用,2014,34(5):1494-1498.
Application of improved anisotropic diffusion model in image filtering and denoising*
ZHANG Chang-sheng1, FENG Guang1, LIU Zi-yu2, LI Chuan1, QIAN Bin1
(1.Faculty of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China; 2.China Energy Engineering Group,Yunnan Electric Power Design Institute Co Ltd,Kunming 650051,China)
To enhance image filtering denoising effect for boiler water level gauge and improve image clarity to better study image recognition later,an improved anisotropic diffusion model filtering algorithm is given through analyzing filtering denoising algorithm such as P-M anisotropic diffusion model,selection diffusion model and You Yu-Li and Kaveh M fourth-order partial differential equations.The proposed algorithm makes diffusion functions of Perona and Malik equalization and introduce standard deviation and regards as deviation margin of gradient expectation value, combines with the covering edge feature of the anisotropic diffusion P-M model and eliminates the ladder defect due to the traditional algorithm overshoot so that the image useful information can be kept and pixel smoothness.The experimental result shows that the proposed filtering algorithm can better reduce the impact of noise on target signal extraction and improve image recognition robustness and enhance effect of image smooth filtering,and image edge clarity and integrity of boiler water level gauge.
filtering and denoising; level image recognition; improved anisotropic diffusion model algorithm; edge feature
10.13873/J.1000—9787(2017)04—0157—04
2016—06—21
云南省中青年学术和技术带头人后备人才项目(2012HB011);昆明理工大学学科方向建设研究项目(14078212)
TP 391
A
1000—9787(2017)04—0157—04
张长胜(1970-),男,副教授,研究生导师,从事智能与光纤检测研究工作,E—mail:ttztty@sina.com。

